单站被动目标观测角优化模型的建立与仿真研究

袁俊华，年福耿，宋 岑，余 升，刘李楠

（海军蚌埠士官学校，安徽蚌埠 233012）

0 引言

单站被动目标定位是指利用一个观测平台对目标进行被动或无源定位的技术。由于仅依靠一个观测平台所能获得的信息量有限，单站被动目标定位实现难度相对较大。但与主动或有源探测定位系统相比，被动定位系统具有作用距离远、隐蔽接收、不易被对方发觉等优点。在越来越强调武器系统实施隐蔽攻击和硬杀伤的趋势下，采用被动方式工作的无源定位作为定位方法发展的主流和对现有定位系统的完善，正越来越受到人们的重视[1]。目前国内外的主要成果是针对固定或者匀速目标研究跟踪系统观测平台的轨迹优化问题和定位方法[1-6]。而针对观测平台实际运动中受到的约束条件及观测角优化考虑较少。本文在对单站定位理论模型反复检验后发现，方位角的微小误差会导致预测目标与实际位置相差甚远。为此提出利用两目标间距离与方位角的函数关系，建立单站被动目标观测角优化的模型，以减小观测系统误差对定位的影响。最后通过两种预处理方法对比及仿真，验证了该模型较传统的卡尔曼滤波算法更有效。

1 问题描述

假定目标和观测平台都在同一平面上，目标沿直线匀速运动，其在水平和竖直方向的分速度为vx，vy，发现时初始坐标为(X0,Y0)，观测平台的初始坐标为(x0,y0)，在某个时刻ti，目标位于(Xi,Yi)，观测平台位于(xi,yi)，目标的观测方位角(正北方向为0°，顺时针为正)为 βi(i=1,2,…n)，如图1。

本文使用优化的角度信息 β̂i(i=1,2,…n)对目标的运动参数进行估计。为保证无源单站的可观测性，观测站必须做一定的机动航行[7]，本文采用匀速直线折往返运动模式，每3分钟观测一次，在单程运动期间，至少观测4次。

由假设目标作匀速运动，其在任一时刻ti的运动方程为：

其理论观测方位线的正切值为：

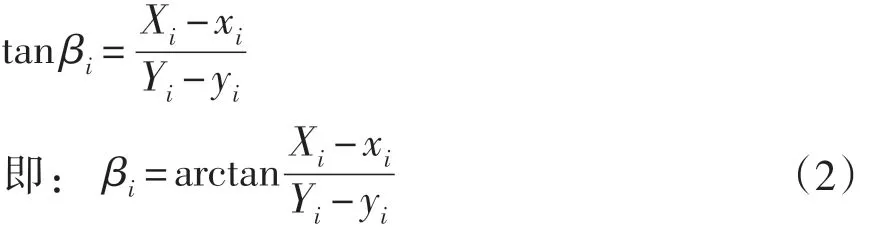
将（1）代入（2）化简得：

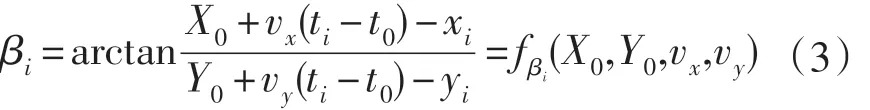
（3）是关于X0,Y0,vx,vy的非线性函数，如果有足够多次观测，例如四次观测βi(i=1,2,…4)，便可得到四个观测非线性方程组，求出X0,Y0,vx,vy，就可以对目标作出定位。但由于各种因素的影响，在方位角的观测时，会存在偏差，记偏差角为εi(i=1,2,…n)。则（3）转换为

但方位角εi的偏差值较小且不易计算（见图1），可用目标实际点到方位线的距离di来代替方位角的偏差。经证明di的表达式为：

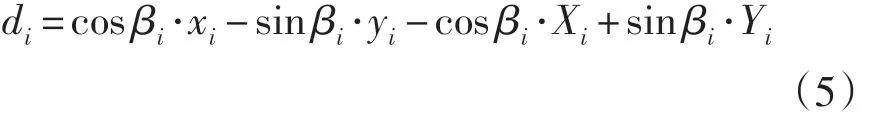
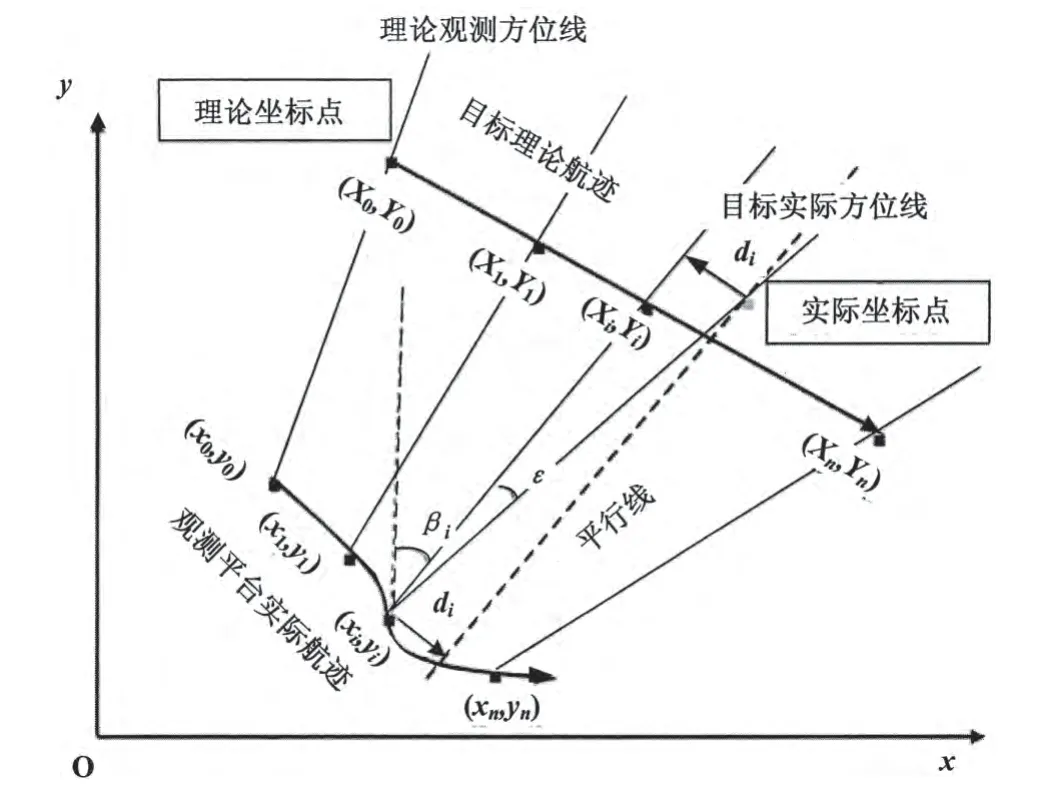
图1 理论方位线和实际方位线

2 模型建立与求解

由于每个点的方位差各不相同，为了找到目标的真实轨迹，利用最小二乘法，求出使方位差di的平方和最小的X0,Y0,vx,vy，便可建立单站定位的理论模型如下：

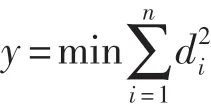
其中

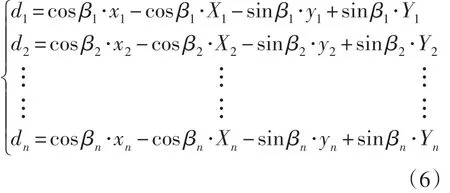
利用MATLAB对模型进行求解，得到4个未知量X0,Y0,vx,vy，即可得出目标的初始位置及运动轨迹。求解主要程序如下：

3 模型的仿真检验

由于观测平台航速及初始坐标已知，由目标航速及初始坐标，推算出每3分钟对目标观测一次方位角 βi（i=1…12）的理论值，将 βi代入模型(6)中，利用MATLAB对其求解，得到4个未知量X0,Y0,vx,vy，即可得出目标的初始位置及运动轨迹，结果见图2。仿真检验发现，模型计算的结果与原题假设完全一致，说明单站定位的理论模型准确性非常高。

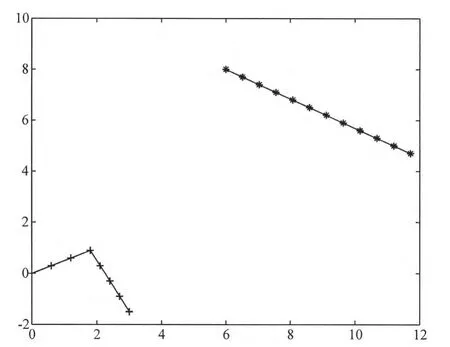
图2 模型得到的目标航行轨迹

4 模型改进

对理论模型检验发现，方位角的误差甚至是微小误差会导致预测的目标与实际位置相差甚远。究其原因，一是由于环境等客观因素影响造成观测者的人为误差，二是由于观测设备精确度不足所产生的误差。因此，本文提出用函数拟合和卡尔曼滤波两种方法对观测值进行预处理，优化观测角来减小观测系统误差对模型计算结果的影响。

4.1 观测值的预处理

4.1.1 函数拟合

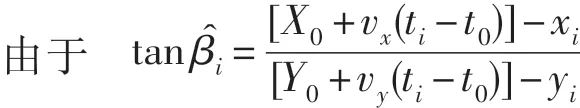
化简得观测角函数优化模型

利用（7）式对观测角 βi进行函数拟合，可求得方位角修正值β̂i。其修正主要程序如下：

4.1.2 卡尔曼滤波

卡尔曼滤波算法模型[8]：

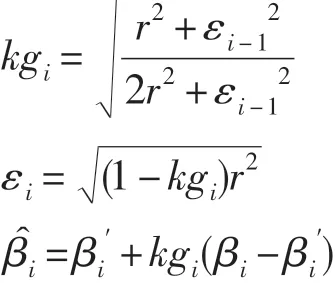
其中kgi是第i次测量得到角度偏差修正的估计系数，εi是测量得到角度偏差，r为测量误差，βi为观测值，βi′通过等差数列公式递推得到。

以第一段实际观测数据 βi为例，利用MAT⁃LAB对数据βi做函数一次拟合与插值得等差数列βi

′，见表1。假设观测误差为1°，将ε0=0代入卡尔曼滤波模型，得：

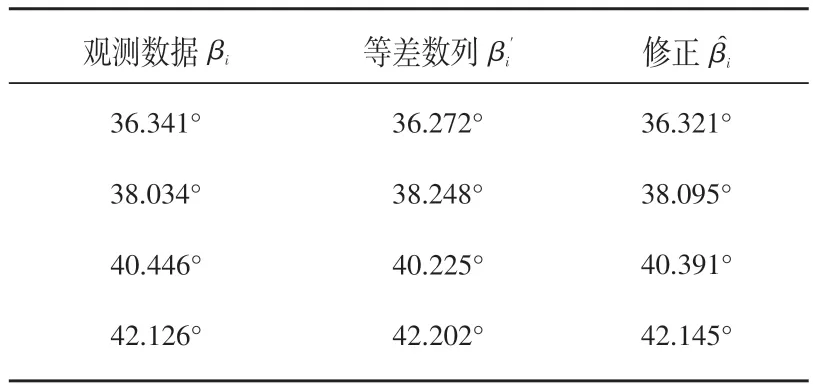
表1 卡尔曼滤波对观测误差为1°数值进行修正

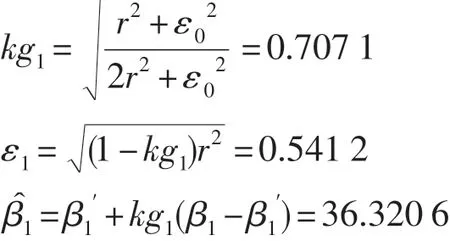
4.2 两种预处理方法对比

本文利用函数拟合和卡尔曼滤波对观测方位角预处理后，在模型中添加约束条件，分别对不同观测距离、不同观测间隔、不同角度误差及不同速度约束，进行200次仿真检验，其中当观测距离20海里、无速度约束、误差0.5o时，利用函数拟合方法定位误差在5%以内达80%，卡尔曼滤波预测是62.5%，其他结果见图3、图4（本文将定位的误差在5%以内的结果认定为可接受范围）。对比两种预处理方法，可见自定义函数拟合预处理比卡尔曼滤波预测得到的结果要好得多。结果同时表明该模型具有较好的收敛性，在方位估算精度为0.5°时，被动定位能与主动方式媲美。

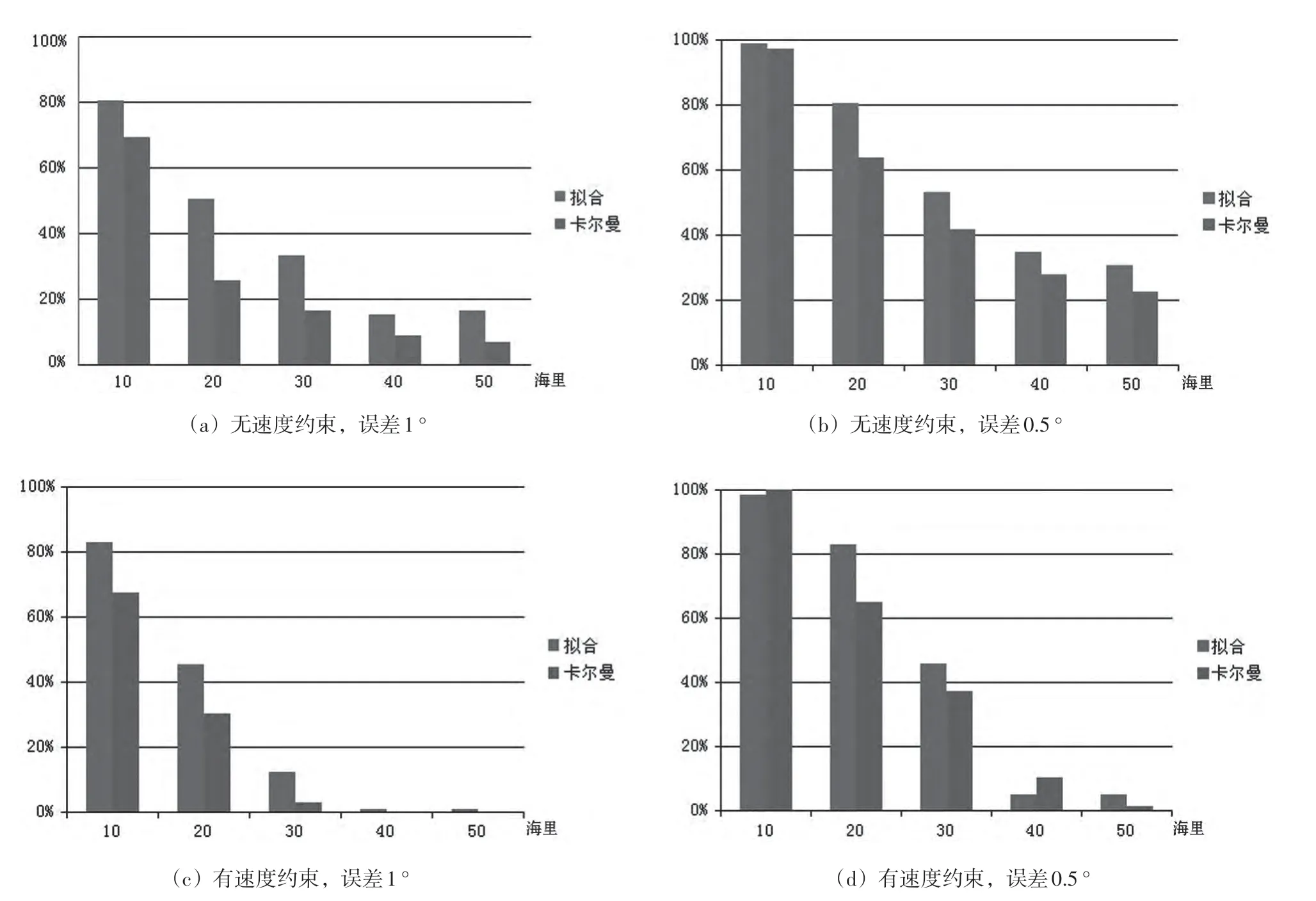
图3 误差1°和误差0.5°模拟200次统计结果

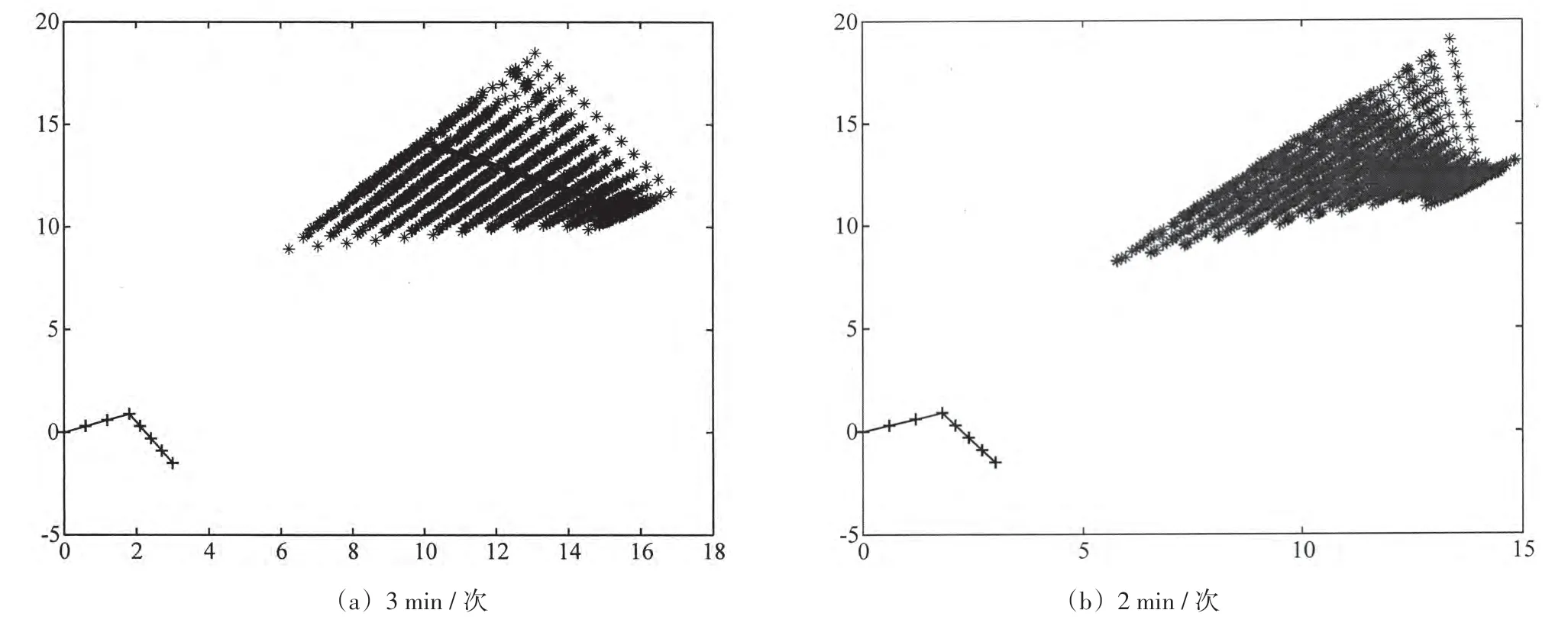
图4 不同观测时间间隔的200次仿真检验结果及收敛情况

5 结束语

近年来单站被动定位理论发展较快，但由于种种原因，如测量误差、设备精度导致理论模型的实际应用效果不佳，本文从观测角优化研究入手，得到较好的定位效果。但文中观测平台仅采用直线折往返式运动，相信一定存在更好的机动方式和观测数据优化方法，以提高被动定位的精度，这方面研究有待进一步深入。

［1］孙仲康，郭福成，冯道旺，等.单站无源定位跟踪技术［M］.北京：国防工业出版社，2008.

［2］汤扣林，刘韵，赵春东.单站测向定位技术研究［J］.火力与指挥控制，2009，34（12）：112-116.

［3］单月晖，孙仲康，皇甫堪，等.单站无源定位跟踪现有方法评述［J］.航天电子对抗，2001（6）：4-7.

［4］熊鑫，章新华，高成志.水中目标被动定位技术综述［J］.舰船科学技术，2010，32（7）：119-125.

［5］冯国强，李伟仁，李战武.机载红外搜索跟踪系统被动定位滤波算法研究［J］.红外与激光工程，

2005（5）：606-611.

［6］王鼎，张莉，吴瑛.基于角度信息的结构总体最小二乘无源定位算法［J］.中国科学F辑，2009，

39（6）：663-672.

［7］许志刚，盛安冬，陈黎，等.被动目标定位系统观测平台的最优机动轨迹［J］.控制理论与应用，2009，

26（12）：1337-1344.

［8］彭丁聪.卡尔曼滤波的基本原理及应用［J］.软件导刊，2009，8（11）：32-34.