椭圆插补在数控系统中的应用

乐艳红，黄扬根

（广州数控信息科技有限公司，广东广州 510663）

0 前言

随着科技的不断进步和工业产品日益多样，加工零件中日渐增多带有复杂曲线的工件产品。复杂曲线包括二次样条、三次样条等多次样条曲线及二次曲线，其中二次曲线中的椭圆、抛物线、双曲线产品需求逐渐增大。而常见的数控系统只具有直线和圆弧插补功能，对于二次曲线轮廓的加工编程，通常都是采用宏程序编程即根据二次曲线的方程将加工工件的曲线拆分成无数段小直线来拟合，这种方法由于二次曲线的中的椭圆、双曲线方程较为复杂，这也对操作工人的要求较高，而用宏程序加工由于编程程序较长，导致运行效率低，加工精度差。本文介绍了椭圆插补的实现原理，使用这种椭圆指令加工椭圆的方法，具有编程简单，加工速度高，精度好等优点。

1 椭圆指令介绍

编程格式：

G6.2/G6.3 X(U)__Z(W)__A__B__Q__

指令字说明：

A：椭圆长半轴长(单位：mm/inch)；

B：椭圆短半轴长(单位：mm/inch)；

Q值是指在右手直角笛卡尔坐标系中，从Y轴的正方向俯视XZ平面，Z轴正方向顺时针方向旋转到与椭圆长轴重合时所经过的角度，如图1所示：

2 实现原理

（1）椭圆中心的计算

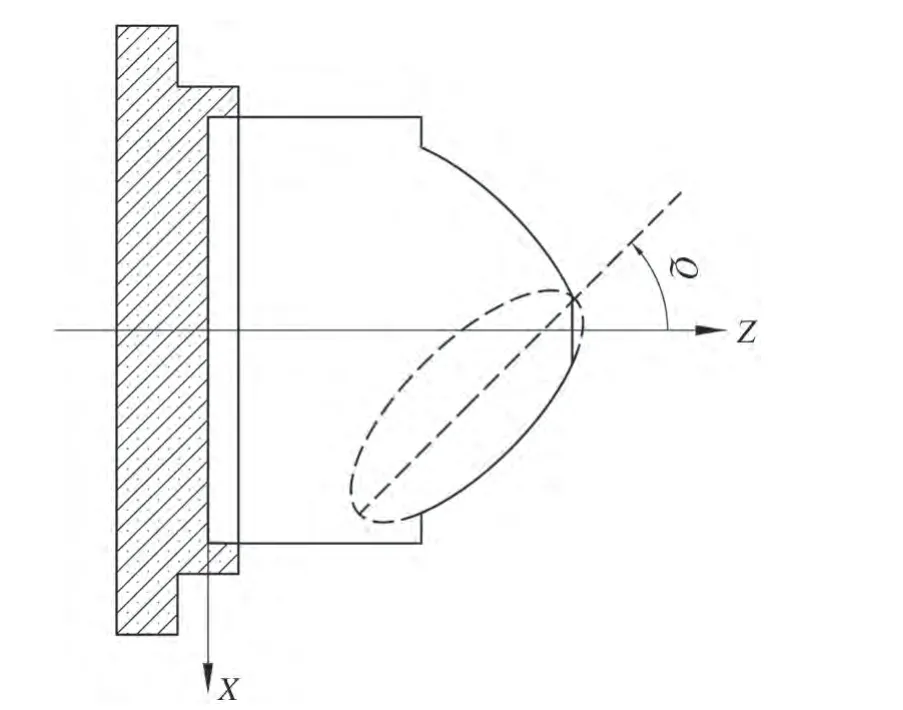
图1 前刀架坐标系

图2 后刀架坐标系

根据编程格式中的已知条件，椭圆的起点X（x1，z1），终点Z（x2，z2），与对称轴的夹角为α，椭圆的长半轴和短半轴分别是a，b，可计算出椭圆中心O（m，n），这样就可得出椭圆方程。可由以下两个方程可求出椭圆的中心O（m，n）：

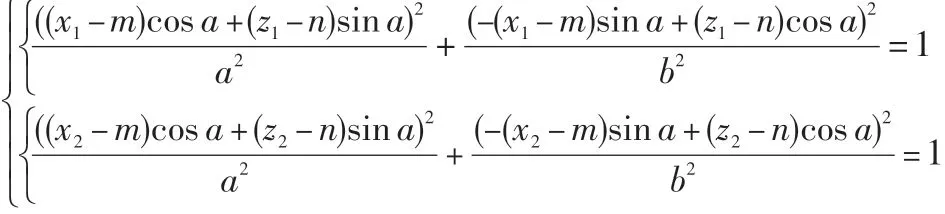
（2）椭圆插补的计算

过点A(xi,zi)为本次插补点，为下次插补点，以弦长AB代替弧长AB，有AB=FT。过A点作椭圆切线与过B点做X轴垂线相交于E点，过A点作Z轴切线与BE交于P点。|AP|为本次插补坐标增量Δxi，|BP|为Z轴坐标增量Δzi。有椭圆方程可得到过A点的斜率，由于插补周期内|AB|很小，近似|AE|=|AB|所以可计算出Δxi，算法如下：

椭圆方程：

5.经营收支结余弥补不正确。如经营收支不匹配，经营结余未进行分配，经营亏损用事业基金弥补。这种处理不符合《事业单位会计制度》的规定。主要是会计人员不熟悉业务导致。

椭圆算法

当 ||b2xi≤ ||a2zi时，斜率小于1时，先求X

当 |b2xi|≻| a2zi|时，斜率大于1时，先求Z

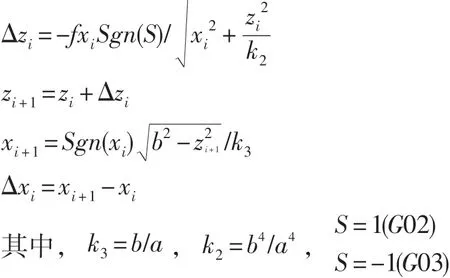
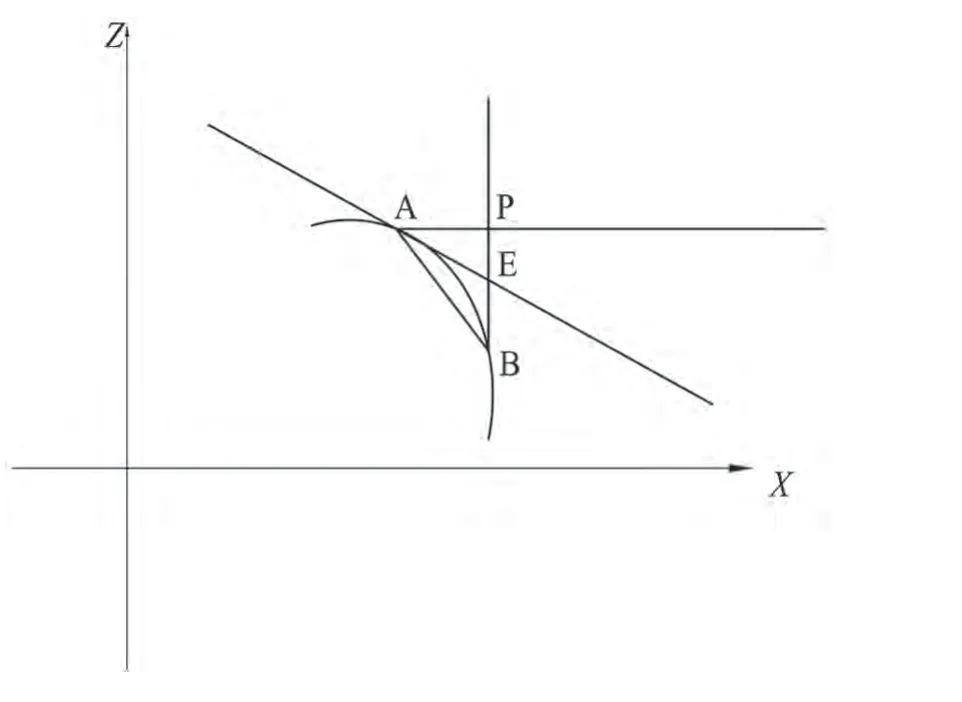
图3 插补原理示意图

3 编程方法对比

针对下图加工图纸中的椭圆，用现在所有系统通用的宏程序编辑方法和本论文采用指令代码编辑程序的方法，从编辑程序上作对比。

（1）宏程序编辑如下：

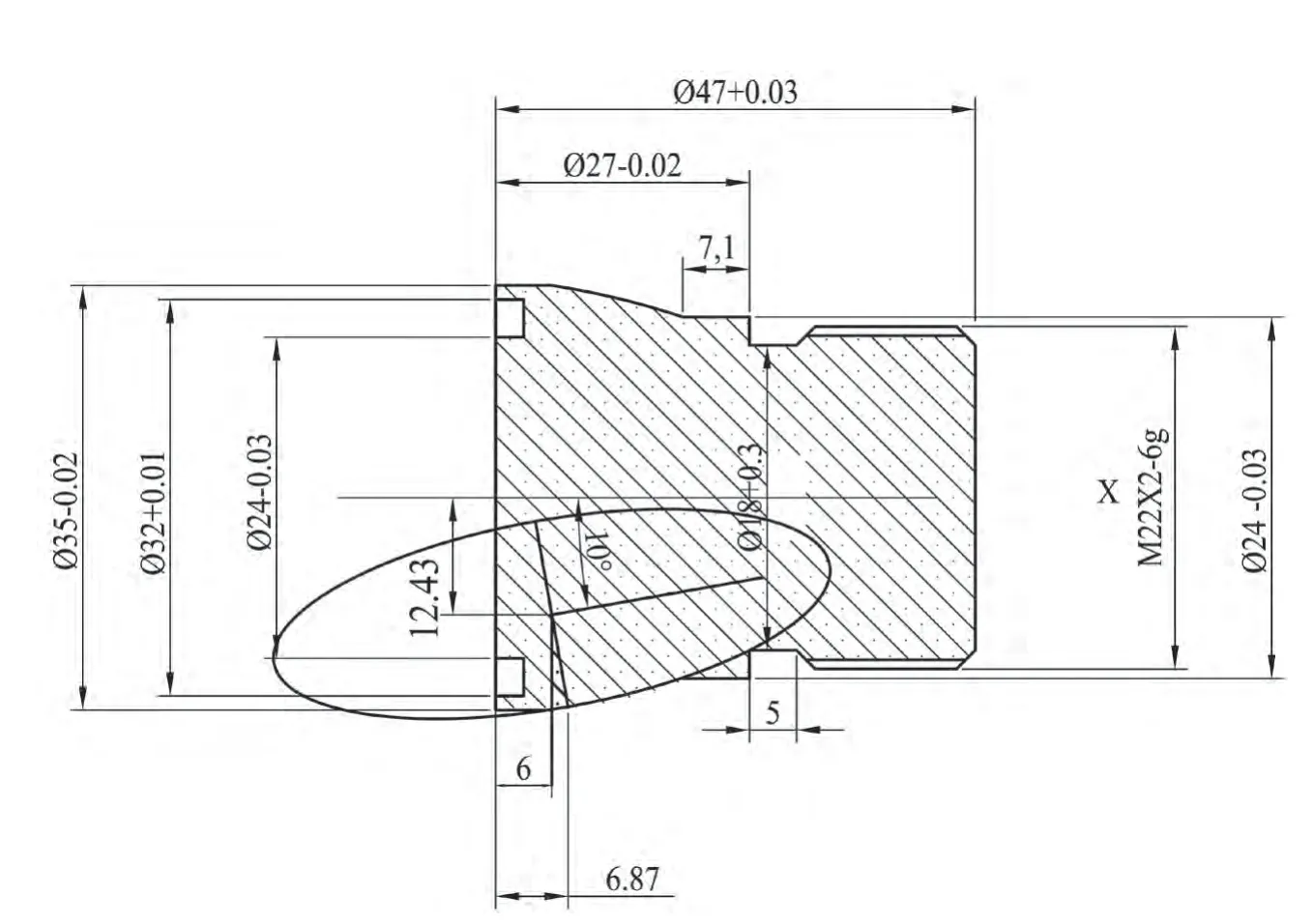
图4 椭圆加工图纸

从加工程序上可看出，用户用宏程序编辑必须知道椭圆方程，并要一步一步给出每个点的计算过程，编辑也很复杂。而对于本论文的方法，用户无需了解椭圆方程，也无需关心怎么计算每个点的构成，只需给出椭圆的常规参数即可。

4 精度、效率对比

控制精度和速度的测试采用LabVIEW虚拟测试平台。测试时测试平台通过数据采集设备对系统伺服轴X轴和Z轴两个轴编码器的进行数据采集，并通过专用的测试软件程序labview对数据进行监控与分析，判断其实际输出曲线与理论曲线的偏差，以及脉冲输出速度波形图。

测试硬件结构图如图5所示。

（1）精度对比

目前大多数系统采用的是宏程序编辑，对于倾斜的椭圆，椭圆的方程比较复杂，编辑宏程序的计算过程难度很大，给客户造成了很多的麻烦。宏程序的编辑实际上是用无数段小支线来拟合椭圆轨迹，其中步长选用多大，对椭圆的轨迹和速度都有很大影响，步长太小精度提高了，但是速度就很慢，如果步长大了，速度提高，精度就很差。而用本论文的编辑程序，只需客户提供图纸上的尺寸，剩下的计算全由CNC数控系统来完成，减少了用户编程的麻烦。

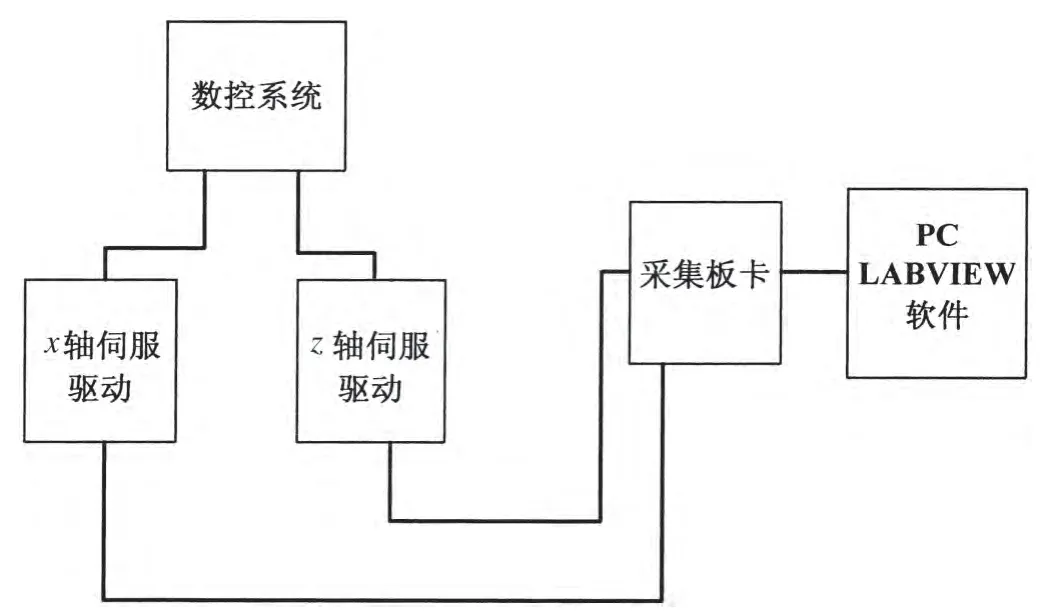
图5 测试结构原理图

通过测试平台，针对“3编程方法对比”提供的程序，在相同的速度下F200，并且两个程序都是针对同一段椭圆进行加工，测试得到的轨迹图如图6所示。从图6可看出，绿色轨迹与红色轨迹相差较大，由于宏程序编辑过程中较多计算造成了加工过程的椭圆的误差较大。最大处误差达到0.1 mm。

（2）效率对比

同样用“3编程方法对比”提供的同一段轨迹的两种编程方法，相同的速度情况下，通过测试平台测试到的速度图见图7和图8。

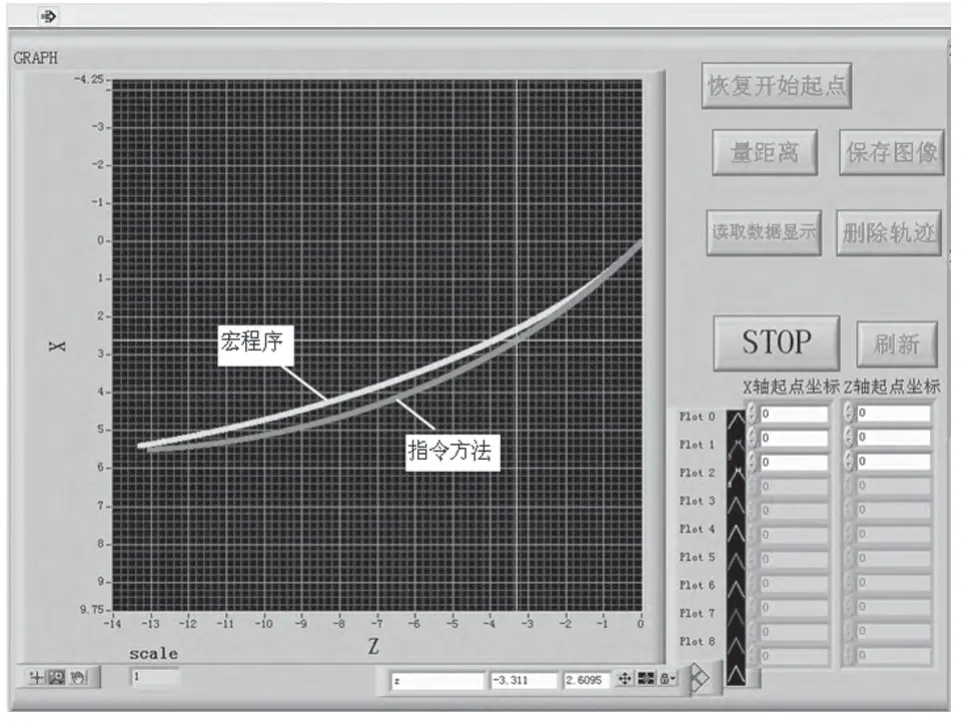
图6 宏程序和指令方法轨迹图的对比

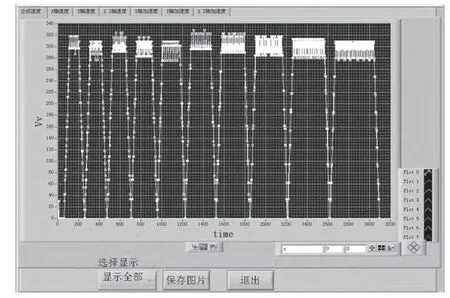
图7 宏程序速度图

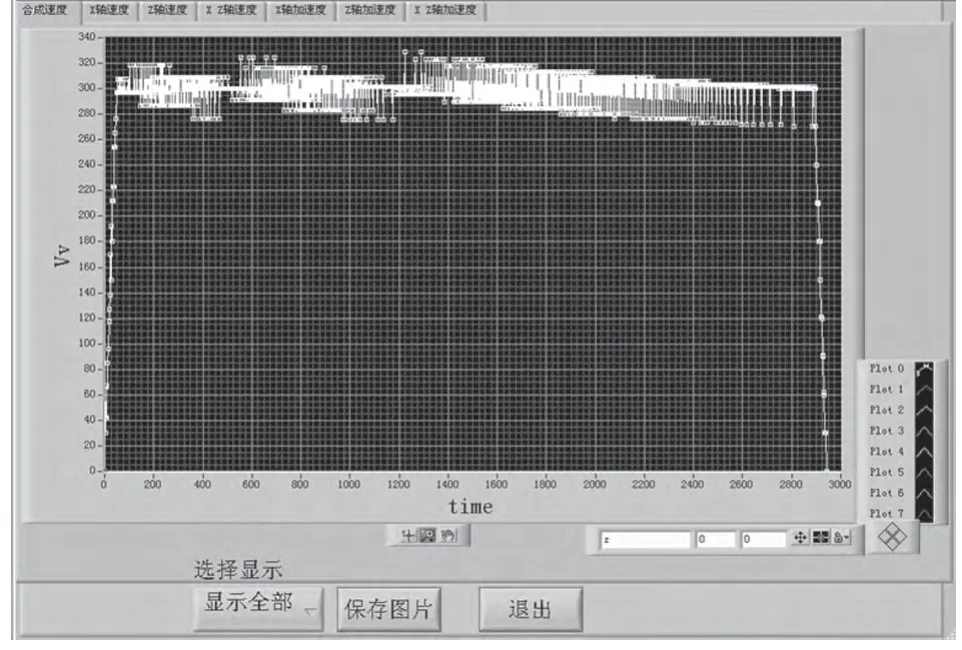
图8 指令速度图

从图7可看出，由于用宏程序编辑的椭圆是由无数段小线段组成，虽然每小段的速度能达到程序所指定的速度但是每段之间都会有速度的跌落，并且速度降到了0，这就造成了工件在加工过程中机床会有暂停的现象加工完成后工件表面会有很明显的痕迹，光洁度不好，同时加工的时间也较长，需要3 100 ms。

从图8看出，程序的速度图只有加速、匀速、减速3个过程，速度维持在300 mm/min，没有速度跌落，这样机床在加工过程中就不会出现暂停现象，加工出来的工件表面的光洁度一致性比较好。由于没有了速度的跌落，加工效率就提高了很多，加工时间只需要2 900 ms，效率提高了百分之六。

5 机床加工测试

本文采用数控系统980TDc-V配沈阳一机HTC2050im，进行实际椭圆加工，机床结构图如图9。

图9 加工机床中心

加工工件如图10。

图10 加工工件

加工椭圆部分

加工工件经过检测，工件表面比较光滑，刀具纹路基本不明显，表面粗糙度为Ra0.8，轮廓误差在5u左右。

6 结语

本功能已正式在笔者公司研发成功并正式发布，并得到广大用户使用及认可。

［1］王爱玲，张吉堂，无雁.现代数控原理及控制系统［M］.北京：国防工业出版社，2004.

［2］李杰，王丹萍，李惠光，等.一种实用快速椭圆插补新方法［J］.东北重型机械学院学报，1994，18（3）：256-259.

［3］GSK980TDc数控系统使用手册［M］.广州数控设备有限公司，2011.