求解VRPSDP的变邻域混合遗传算法

马 欢,张建伟,赵进超,陈 明

(1.郑州轻工业学院软件学院,郑州河南450002;2.郑州轻工业学院计算机与通信工程学院,郑州河南450002)

求解VRPSDP的变邻域混合遗传算法

马 欢1,张建伟1,赵进超2,陈 明1

(1.郑州轻工业学院软件学院,郑州河南450002;2.郑州轻工业学院计算机与通信工程学院,郑州河南450002)

针对卸装一体化车辆路径问题，提出一种结合变邻域下降搜索和遗传算法的混合启发式算法(GA_VND).利用随机生成的初始种群，通过遗传算法的交叉变异操作生成弱可行解种群，选择其中的最优值作为变邻域深度搜索的初始解.在变邻域深度搜索的过程中通过两种不同的局部搜索算子对解进行局部搜索和迭代优化.通过对54个算例的求解，仿真结果表明GA_VND更新了54个已知最好解中的8个，表明了该算法是解决卸装一体化车辆路径问题的一种有效方法.

卸装一体化;车辆路径问题;变邻域下降搜索;遗传算法;组合优化

0 引言

卸装一体化车辆路径问题(Vehicle Routing Problem with Simultaneous Delivery and Pickup, VRPSDP)普遍存在于物流运输中,该问题的解决对于减少物流成本,提高物流效率具有重要意义.由于VRPSDP同VRP问题都属于NP难题［1］,因此目前国内外对于VRPSDP的研究主要集中在各种元启发式算法和混合式的启发算法上,在元启发式算法方面:国内外的专家学者多采用遗传算法［2］、蚁群算法［3］、粒子群算法［4］、模拟退火算法［5］等来解决这一问题.在混合启发式算法上,苏孟洛等［6］提出结合粒子群算法和变邻域下降搜索的混合粒子群算法;Y.M等［7］提出结合禁忌搜索和蚁群搜索算法的混合算法;Zachariadis等［8］提出导引式局部搜索和禁忌搜索相结合的混合算法.这些算法虽然都取得了一定成果,但其求解质量仍有一定的改进空间.

将遗传算法和变邻域下降算法相结合,提出一种混合启发式算法GA_VND用于求解VRPSDP问题.利用54个基准测试算例进行实验,并与文献［8］以及文献［9］中的算法求解结果比较,验证本文算法的有效性.

1 问题描述

1.1 问题描述

定义设有向带权图G=(V,A,C),其中V={i｜i=0,1,…,n}是节点集合,节点0为出发地节点,(1～n)为客户地节点;A={i,j｜i,j∈V}表示弧集,C={cij｜(i,j)∈A}为权重矩阵,cij表示节点i到节点j的距离.每个客户节点i都有卸货需求di和装货需求pi,运输车辆的最大载货量为Q. VRPSDP则可以描述为:①每辆车都从0点出发,服务若干客户后返回0点,形成一个解S;②每个客户都仅被服务一次,而且只能由某一车辆提供服务;③每个车辆的载重量都不超过Q;④所有客户的装卸货需求都不超过Q;⑤总的运输距离f(S)最小.

1.2 解的可行性定义

对于VRPSDP的解S={rj｜j=1,2,…,k},其中rj={i｜i∈［1,n］},表示车辆j的路径,k为解中最大的车辆数.S是强可行解的充要条件:车辆在访问过rj上所有客户后载重都不超过Q.对于解S,∃ri∈S不满足约束条件,则解S是一个弱可行解;∀ri∈S不满足约束条件,则解S是一个不可行解.

2 GA_VND算法

2.1 遗传算法搜索全局生成强可行解的步骤

STEP1:最近邻法生成遗传算法初始强可行解S0.步骤为:①从未被选择的客户节点集合中选择距离出发节点最近的节点,开始一条新路径;②从未被选择的客户节点集合选择距离路径上最后一个节点最近的节点;③若加人节点后路径满足强可行解约束条件,则返回第2步,否则返回第1步.

STEP2:将STEP1生成的强可行解作为父代染色体,通过交叉生成多个子代染色体,即构造了多个可行解.步骤如下:①将该强可行解存人子代种群中;②从父代染色体上随机选取客户节点作为交叉节点;③进行染色体交叉和变异运算生成新的染色体.随机选择交换和插人两种方式进行交叉标点.

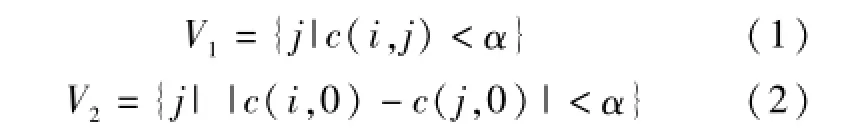
上述公式需满足i≠j,i,j∈V和i,j≠0.α= f(S0)/n,S0为STEP1生成的强可行解.变异操作采用贪婪倒位变异的方式:随机选择变异点i,在不包含节点i以及节点i的左右两个节点i_left和i_right的集合中选择距离节点i最近的节点j,将i_right和j之间的节点逆向排列.例如:解为(1, 2,3,4,5,6,7,8,9),随机选择节点4,距离节点4最近的节点为8,倒位变异解后为(1,2,3,4,8,7, 6,5,9).通过交叉和变异生成的染色体不一定满足强可行解的约束条件,因此需要将其进行转化为强可行解.④判断当前生成的染色体总数是否到达种群上限,是则判断新种群中是否有优于父代染色体的子代染色体,有则选择其中所有优于父代染色体的子代染色体进人STEP3,否则返回STEP2,并扩大距离参数α.

STEP3:利用Chen J.F.［10］的方法将解集中的弱可行解转化为强可行解.方法如下:扫描解中的每一个客户节点,如果满足强可行解的约束条件,则继续扫描,否则记录该节点,直到节点全部扫描完.扫描完成后将上次扫描中被记录的节点从路径中删除后再按照逆序重新加人路径,即可得到一个强可行解.选择转换后的强可行解集中的最优解作为变邻域下降搜索的初始解.

2.2 变邻域下降搜索局部最优解

变邻域下降搜索将从2.1中获得的强可行解作为初始解,随机选择一种邻域结构进行局部搜索,当到达迭代次数上限或者连续无改进迭代次数到达上限时结束搜索.这里选择两种邻域结构:插人(insert)和2-opt.插人是将解S中的客户i从当前位置li移动到另一个位置lj,从而产生一个新解.位置li和lj上的节点属于解S中的任意路径.2-opt是对于解S中的同一路径上位于li和lj(li＜上的两个客户,将li+1位置上的节点与位于lj上的节点交换位置,并将li+1到lj之间的节点按逆序排列.两种结构如图1所示:

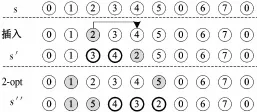
图1 邻域结构:插入和2-optFig.1 Neighborhood structure:insert and 2-op t

两种邻域结构的随机选择可以结合两种邻域不同的寻优能力,同时也可以在一定程度上扩展算法的搜索空间.

2.3 GA_VND算法

首先需要定义相关参数:遗传算法染色体种群数max_chom,最大迭代次数max_i,交叉概率pc,变异概率pm,GA连续无改进迭代次数nobetter _ga_i=max_i/4,VND连续无改进迭代次数nobetter_vnd_k=n/2.GA_VND算法伪码如下:

1.初始化参数:max_chom,max_i,pc,pm, nobetter_ga_i,nobetter_vnd_k;

2.定义变量:迭代次数i=0;GA当前无改进迭代次数j=0;VND当前无改进迭代次数k=0;

3.WHILE(i＜max_i)DO

4.按照2.1节STEP1构造初始强可行解Si;

5. Sbest=Si;α=f(S0)/n;

6. WH ILE(j＜nobetter_ga_i)DO

7. S0=Sbest;//S0为VND的初始解

8.以S0为父代染色体按照2.1中的STEP2和STEP3方法生成新种群;

10.WHILE(k＜nobetter_vnd_k)DO

12. IF(f(Sk)＜f()

13. S0new=Sk;

14. k=0;

15. ELSE

16. k++;

17. End IF

20. Sbest=;

21. j=0;

22. ELSE

23. j++;

24. α=α×1.1;

25. End IF

26. End WHILE

27. i++;

28.End WHILE

29.输出Sbest,算法结束;

3 实验结果及分析

3.1 测试用例

为了测试GA_VND算法的性能,主要采用两种类型的测试数据进行实验:随机取数的Dethloff算例［11］、Salhi和Nagy算例［12］.Dethloff算例为随机生成的40个问题规模均为50的算例.根据客户分布和车辆需求可以分为SCA3x,SCA8x, CON3x,CON8x.其中SCA算例为［0,100］间均匀分布,CON算例为［0,200］间非均匀分布.各客户点的卸货需求d为在［0,100］间取随机值,装货需求p为(k+0.5)*d,其中k在［0,1］间取随机值.Salhi和Nagy算例的问题规模在［50,199］之间,每个问题包含两个算例,其中CMTxX为在原CMTx算例基础上增加了装卸货需求的算例［10］, CMTxY为和CMTxX装卸货需求相反的算例.

GA_VND算法采用c#在.net平台下实现,运行环境为WIN7 64x,CPU为Intel core i5-2520M 2.5 GHz,内存为6G,参数设置为max_chom= 100;max_i=200;pc=0.5;pm=0.05;nobetter_ga _i=50;Dethloff算例中nobetter_vnd_k=25.Salhi和Nagy算例中nobetter_vnd_k=n/2,CMTxX和CMTxY的问题规模相同,分别为(50,75,100, 120,150,199).

3.2 算法的可行性分析

以Dethloff算例中的SCA3-0算例为例,设定最大迭代次数为200,对GA_VND算法和VND算法每次迭代求得的当前最优解进行比较,重复运行10次取平均值,结果如图2所示.

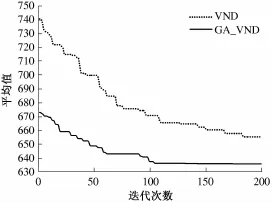
图2 SCA 3-0算例上每次迭代最优解的平均值比较Fig.2 Comparison of the optimal solution's average value by every iterated based on SCA3-0examples

可以看出GA_VND算法中由GA算法求得的初始可行解的存在,使得GA_VND算法可以从一个较优的初始解开始搜索.陷人局部最优时扩展GA交叉范围的机制和VND仅变换邻域相比, GA_VND算法可通过变化初始解来重新求解,跳出当前局部最优,避免了VND算法随机初始解求解的局限性.

3.3 Dethloff算例上的最优解比较

为了验证GA_VND算法的有效性,这里将遗传算法、Zachariadis提出的禁忌搜索和Guided Local Search的混合算法TS_GLS［8］、GA_VND算法应用于Dethloff算例进行计算.表1描述了在Dethloff算例上GA求得的最优解、TS_GLS求得的最优解和GA_VND运行10次取平均值的比较,其中,L为最优路径长度,t为计算消耗时间,单位为s.

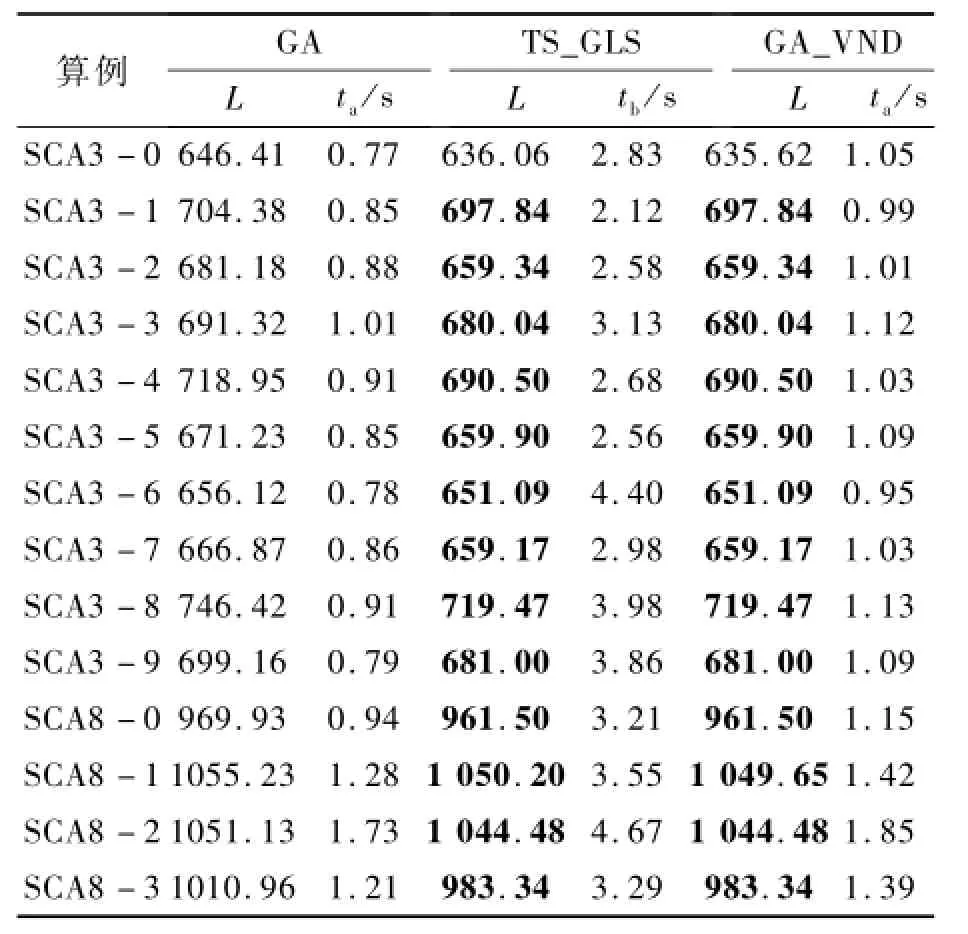
表1 Dethloff算例上的结果比较Tab.1 Comparison of the solutions based on Dethloff

续表1

通过对表1的4组40个测试算例进行计算,其中的已知最好解用粗体标出.通过遗传算法的和GA_VND算法的结果比较可以看出:混合算法GA_VND的求解质量明显高于遗传算法的,通过TS_GLS算法和GA_VND算法的结果比较可以看出GA_VND算法更新了Dethloff算例中的SCA3 -0、SCA8-1和SCA8-7在TS_GLS中的已知最好解,说明GA_VND算法是可行有效的.

3.4 Salhi和Nagy算例上的最优解比较

为了进一步验证GA_VND算法的有效性,采用在Salhi和Nagy算例上将GA_VND算法运行10次取平均值和TS_GLS算法以及C.Yu提出的AIS算法［9］两种算法求得的最优解进行对比,结果如表2所示.

通过TS_GLS算法和GA_VND算法以及AIS算法计算的最优解结果相比较,可以看出:在平均路径长度方面,GA_VND算法较TS_GLS算法减少了0.46,较AIS算法减少了18.73;在最优解的质量上,GA_VND算法较TS_GLS算法最大提高了2.55%,最小提高了0.65%.较AIS算法最大提高了5.35%,最小提高了0.27%,进一步说明了GA_VND算法是可行有效的.

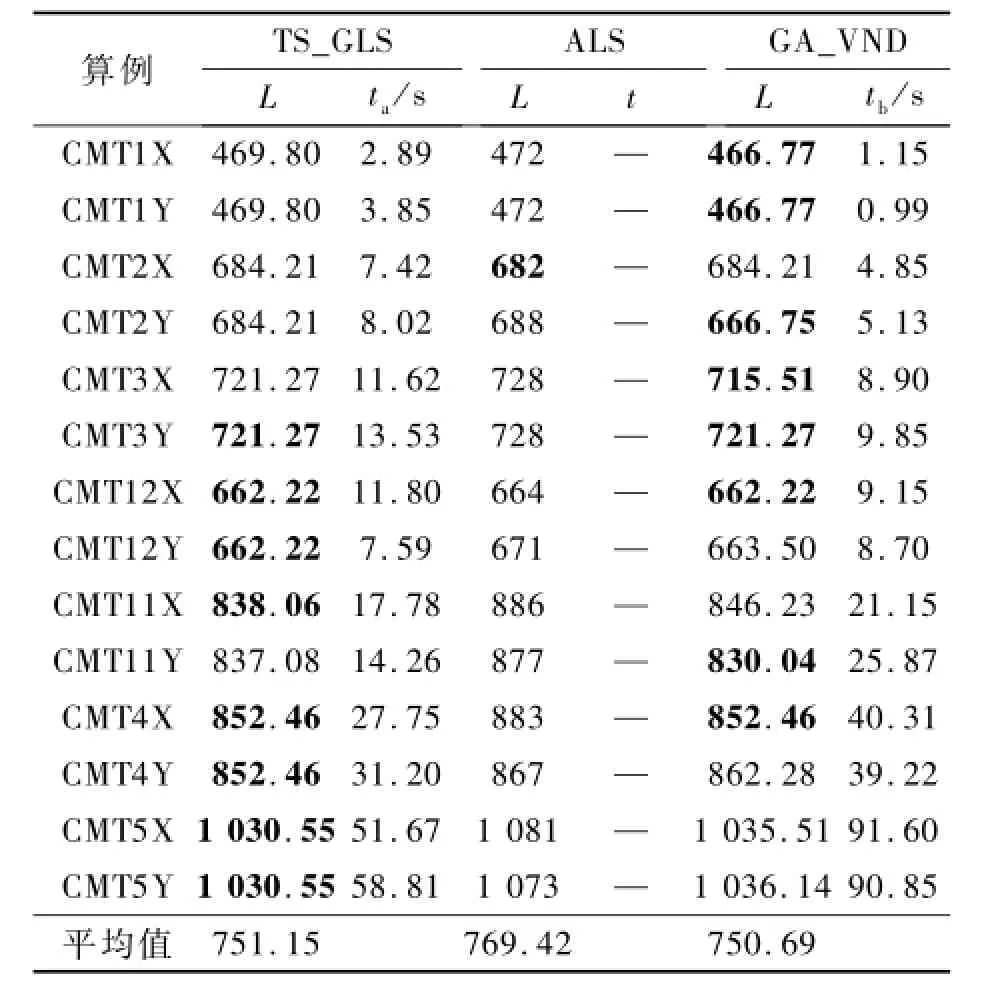
表2 Salhi和Nagy算例上的结果比较Tab.2 Comparison of the solutions based on Salhi and Nagy

4 结论

卸装一体化车辆路径问题是一个有着实际应用需要且广泛存在的问题,针对这一问题设计了一种结合遗传算法和变邻域下降搜索的混合启发式算法,将遗传算法的全局搜索能力和变邻域下降搜索算法的局部搜索能力相结合,有效地提高了求解质量.通过对Dethloff算例和Salhi和Nagy算例共54个算例的求解,验证了GA_VND算法优于单一的遗传算法,且更新了54个算例中的8个当前最优解,表明了本文算法的有效性.

［1］ 叶春明,王科峰,李永林.同时送取货车辆路径问题算法研究综述［J］.计算机应用研究,2013,30 (2):334-340.

［2］ 龙磊,陈秋双,华彦宁,等.具有同时集送货需求的车辆路径问题的粗粒度并行遗传算法［J］.系统仿真学报,2009,21(7):1962-1968.

［3］ GAJPAL Y,ABAD P.An ant colony system(ACS) for vehicle routing problem with simultaneous deliveryand pickup［J］.Computers&Operations Research, 2009,36(12):3215-3223.

［4］ 吴斌,蔡红,樊树海,等.双倍体差分进化粒子群算法在VRPSDP中的应用研究［J］.系统工程理论与实践,2010,30(3):520-526.

［5］ 王超,穆东.物料配送和废旧产品回收的VRPSDP问题的并行模拟退火算法［J］.北京交通大学学报,2014,38(6):19-26.

［6］ 苏孟洛,杨宏安,孙启峰.求解卸装一体化的车辆路径问题的混合粒子群算法［J］.中国制造业信息化:学术版,2012,41(9):52-56.

［7］ YOUSEFIKHOSHBAKHT M,DIDEHVAR F,RAHMATI F.A combination of modified tabu search and elite ant system to solve the vehicle routing problem with simultaneous pickup and delivery［J］.Journal of Industrial and Production Engineering,2014,31(2): 65-75.

［8］ ZACHARIADISE E,TARANTILIS C D,KIRANOUDIS C T.A hybrid metaheuristic algorithm for the vehicle routing problem with simultaneous delivery and pick-up service［J］.Expert Systems with app lications, 2009,36(2):1070-1081.

［9］ YU C,LAU H Y K.AIS-based A lgorithm for Solving Vehicle Routing Problem with Simultaneous Pick-up and Delivery(VRP-SPD)［J］.Journal of Traffic and Logistics Engineering,2013,1(2):174-178

［10］CHEN JF,WU T H.Vehicle routing problem with simultaneous deliveries and pickups［J］.Journal of the Operational Research Society,2006,57(5):579-587.

［11］DETHLOFF J.Vehic le routing and reverse logistics: the vehicle routing problem with simultaneous delivery and pick-up［J］.OR-Spektrum,2001,23(1): 79-96.

［12］SALH IS,NAGY G.A cluster insertion heuristic for single and multip le depot vehicle routing problemswith backhauling［J］.Journal of the Operational Research Society,1999,50(10):1034-1042.

AHybrid Genetic and Variable Neighborhood Descent Algorithm for Vehicle Rou ting Problem with Simultaneous Delivery and Pickup

MA Huan1,ZHANG Jian-wei,ZHAO Jin-chao2,CHEN M ing1
(1.Software Engineering College,Zhengzhou University of Light Industry,Zhengzhou 450002,China;2.School of Computer and Communication Engineering,Zhengzhou University of Light Industry,Zhengzhou 450002,China)

This paper proposes a hybrid heuristic algorithm combing variable neighborhood descent search with genetic algorithm(GA_VND)to solve vehicle routing problem with simultaneous delivery and pickup.By the use of the initial populations generated random ly,the weak feasible solutions are produced by the crossover and mutation operators of genetic algorithm.And then,the best of them was selected as initial solution of variable neighborhood descent algorithm.Finally,in the process of the variable neighborhood descent search,two different neighborhood structures are used to search the locally optimal solution.The simulation results show that GA_VND can update 8 better solutions in the 54 best known solutions,which illustrates that GA_VND is an effective method for vehicle routing problem with simultaneous delivery and pickup.

vehicle routing problem;simultaneous delivery and pickup;variable neighborhood descent;genetic algorithm;NP-hard

TP301

A

10.3969/j.issn.1671-6833.2015.03.026

1671-6833(2015)03-0120-05

2015-01-19;

2015-03-04

国家自然科学基金资助项目(61403349);国家级大学生创新创业训练计划项目(201310462018)

马欢(1981-),男,河南孟州人,郑州轻工业学院讲师,主要研究方向为信息处理,智能与信息系统,E-mail:mahuanresearch@126.com.