预测页岩气产量递减组合模型的研究

刘传斌，姜汉桥，李俊键，糜利栋，赵林，乐雪霖

（1.中国石油大学（北京）石油工程教育部重点实验室，北京 102249；2.中国石油川庆钻探工程有限公司四川石油天然气工程建设有限责任公司重庆分公司，重庆 400021）

0 引言

在页岩气开采过程中，储集层水平井体积压裂后，其生命周期主要分为4个阶段[1]：1）高产期，产量主要来自人工裂缝；2）高速递减期，以达西与非达西流动为主；3）低产低效期，流体主要来自微米-纳米孔隙结构；4）低产无效期，流体以解吸、扩散为主。其中，高产期时间较短，初期产量递减变化迅速，油气田投产不久，就出现产量递减的现象。

利用Arps双曲递减模型分析页岩气生产数据时，通常出现递减指数n＞1的情况，造成累计产量无限大的不合理性[2]。究其原因是，Arps模型适合于达到拟稳定状态的流动，而页岩气层的特低渗、低孔特征不能满足这一要求。另外，页岩气产量第1年的递减率一般超过50%。在页岩气产量预测中，关键的问题是，如何利用短历史时期的生产数据准确预测产量变化，从而指导生产方案设计。

近几年，针对页岩气产量递减问题，国外一些学者如 L.Mattar[3]， D.S.Fulford[4]等，提出了通过改变 Arps模型中的递减指数加以修正的方法。还有学者提出了一些新模型，如 SEPD 模型[5-6]、Duong 模型[7-8]和 YM-SEPD 模型[9-11]，但在实际应用时，均有不足之处，SEPD模型和YM-SEPD模型在后期的预测值偏低，Duong模型的预测值偏高。新模型在数值分析和现场应用中，生产前期预测符合度较好，后期预测准确度逐渐降低。

针对以上问题，本文提出利用组合模型的思路研究页岩气产量递减模型。该思路主要考虑不同阶段主导页岩气产量的机理不同，在前期与后期以不同的递减模型为研究内容，前期选择以SEPD模型、Duong模型和YM-SEPD模型为主，后期以SEPD模型和Arps模型为主。

1 产量递减分析方法

1945年，Arps提出了递减曲线分析方法，已被广泛应用于常规油气的产能预测[10]。 Lee，Sidle 等[11-12]利用Arps递减关系分析页岩气井产量时，总是出现递减指数 n＞1 的情况。 对于 n＞1，随着 t→∞，则

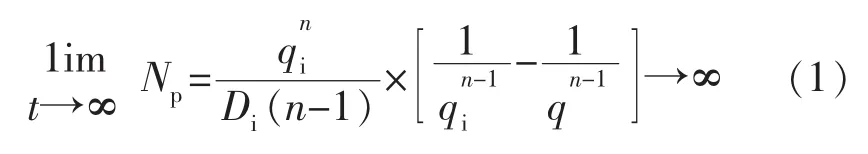
式中：Np为累计产量，m3；qi为最大或初始产量，m3/d；q为某时刻的产量，m3/d；Di为递减率；t为生产时间，d。

由式（1）可知，随着生产时间的增加，产量不断增加，但产量的增加不受时间的限制，不能计算出最后的采收量，有着严重不合理的现象，与实际生产不符。

2009 年，Valko等人[5-6]考虑到影响产量变化的指数规律，提出伸缩指数递减模型（SEPD）。在递减曲线模型中引入了时间常数τ：

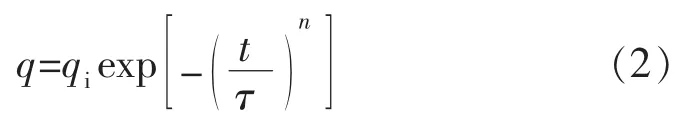
2010 年，Duong 等[7]基于裂缝储层线性流规律，建立了Duong指数递减方程。在双对数坐标系中，产量与累计产量的比值和生产时间呈线性关系。油气在裂缝中的流态主要是线性流和双线性流，考虑生产井的整个周期，裂缝中产量的变化规律可以表示为

对式（3）积分，可以求得累计产气量为

Duong基于裂缝线性流的假设，类比式（4），给出了产率递减方程：

式中：a为递减系数；m为指数系数。

2013 年，S.Yu 等[8-9]通过对比各种方法，考虑到生产井一般只有2～3 a的生产史，引入特征值计算，提高了参数的准确度，提出了修正的伸缩指数递减模型（YM-SEPD）。

为了解决SEPD模型使用时出现的问题，S.Yu等提出了一种修正SEPD模型的方法——引入式 （6）的方程计算2个关键参数n和τ：

2 模型适应性研究

建立典型数值模型，模型参数见表1。利用上述模型对渗透率为0.000 1×10-3μm2进行预测，不同模型的预测结果见图1。

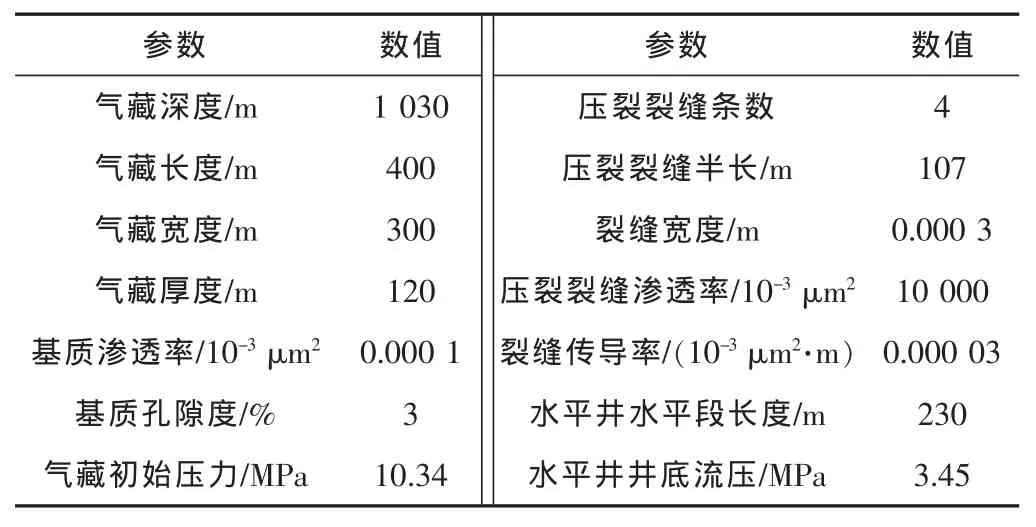
表1 典型模型的基本参数

图1 不同模型产量递减预测

由图1可见，SEPD模型、YM-SEPD模型和Duong模型预测趋势基本一致，预测前期与实际数据吻合度较高，在后期与实际数据的趋势渐渐偏离；在后期，SEPD模型和 YM-SEPD模型预测日产量偏低，而Duong模型预测偏高。在预测20 a时，误差在40%～60%，且误差随着生产时间增加不断扩大。

3 组合模型探讨

鉴于前文分析，尝试探索2种模型相结合进行产量预测，前期以SEPD模型、Duong模型和YM-SEPD模型为主，随着递减率的降低，后期尝试用SEPD模型和Arps模型。

经过优选，选择以下3种组合模型：Duong+Arps模型、SEPD+Arps模型以及SEPD+Duong模型。模型组合点的选择由递减率变化速率来确定，将2种模型递减率变化速率基本相等处定为组合点。

按照这一思路，在渗透率为0.000 1×10-3μm2时，不同组合模型的预测结果见图2。

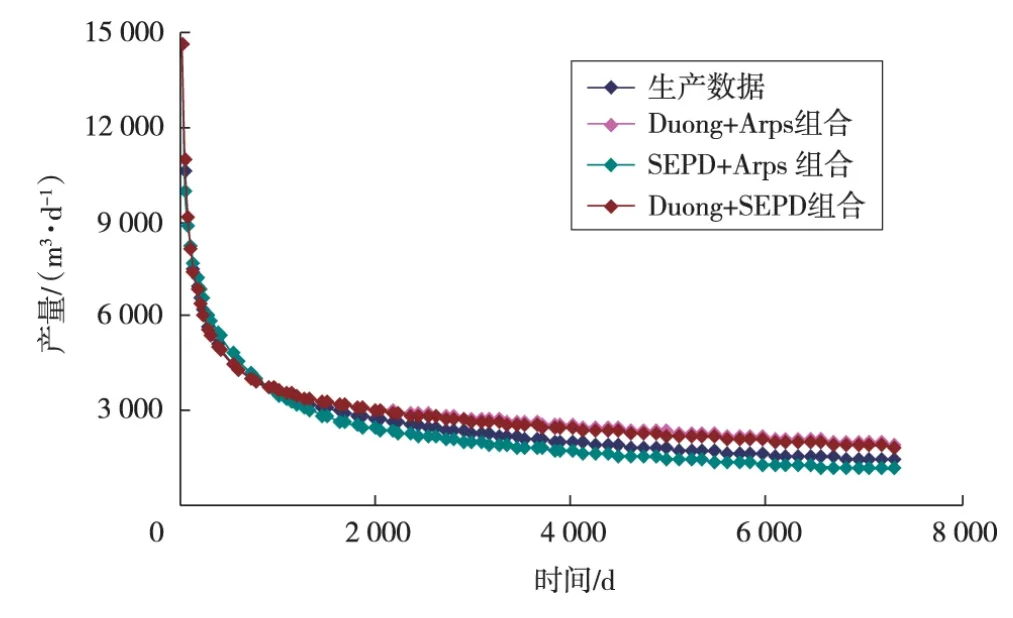
图2 不同组合模型递减产量预测

由图2可以看出，Duong+Arps组合模型、SEPD+Arps组合模型以及Duong+SEPD组合模型预测结果都较吻合。其中以SEPD+Arps组合模型预测精度最高。生产年限达到20 a的预测结果相对误差对比见表2。

表2 数值模拟中生产年限为20 a的预测误差 %

从表2可以看出，相比单一模型，组合模型的预测精度均明显提高。数值模拟证实，SEPD+Arps组合模型预测精度最高，同时，3类组合模型的吻合度均有提高，如何达到最高的吻合度，需要选择合适的组合点。

4 实例验证

加拿大西部沉积盆地Cadomin层系有一口水平井，通过不同方法对其产量进行预测。该水平井位于Alberta，已生产9 a，中间基本无长时间关井。主要地层参数见表3。

根据生产数据预测产量变化趋势。为了便于对比，选择前3 a的历史生产数据，利用上述模型预测产量变化，观测各模型在剩余生产时间内的吻合度。3类组合模型的预测结果见图3。

表3 现场基础资料

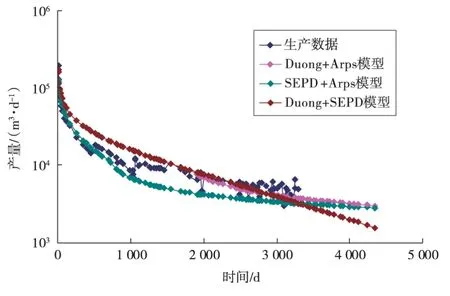
图3 不同组合模型的实例预测

在优化组合模型中，Duong+Arps组合模型与SEPD+Arps组合模型都比较准确地预测了产量变化的趋势，而Duong+SEPD组合模型在后期有着明显的下降趋势。Duong+Arps组合模型与SEPD+Arps组合模型后期预测产量变化趋势基本相同。

5 结论

1）由于页岩气的开采过程很难达到拟稳定流态，Arps双曲递减模型适应性较差。新模型SEPD模型和YM-SEPD模型预测一般较生产数据偏低，Duong模型预测一般偏高。

2）在优化组合模型中，Duong+Arps组合模型与SEPD+Arps组合模型预测结果比较准确，而Duong+SEPD组合模型在后期有着明显的下降趋势。

3）与基础模型相比，3类组合模型吻合度都有提高，但提高组合模型的吻合度关键在于选择合适的组合点，组合点的选择方法仍需进一步探索。

[1]邹才能，张国生，杨智，等.非常规油气概念、特征、潜力及技术[J].石油勘探与开发，2013，40（4）：385-388.

[2]雷丹凤，王莉，张晓伟，等.页岩气井扩展指数递减模型研究[J].断块油气田，2014，21（1）：66-68，82.

[3]Mattar L，Moghadam S.Modified power law exponential decline for tight gas [C].Calgary：Canadian International Petroleum Conference（CIPC），2009.

[4]Fulford D S.Evaluation of time-rate performance of shale wells using the Transient Hyperbolic Relation[R].SPE 167242，2013.

[5]Valko P P.Assigning value to stimulation in the Barnett shale:A simultaneous analysis of 7000 plus production histories and well completion records[R].SPE 119369，2009.

[6]Valko P P，Lee W J.A better way to forecast production from unconventional gas wells [R].SPE 134231，2010.

[7]Duong，Anh N.An unconventional rate decline approach for tight and fracture-dominated gas wells[R].SPE 137748，2010.

[8]Yu S，Lee J W，Miocevic D J，et al.Estimating proved reserves in tight/shale wells using the Modified SEPD Method[R].SPE 166198，2013.

[9]Yu S.Best practice of using empirical methods for production forecast and EUR estimation in tight/shale gas reservoirs[R].SPE 167118，2013.

[10]Arps J J.Analysis of decline curves[J].SPE 945228，1944.

[11]Lee W J.Gas reserves estimation in resource plays[R].SPE 130102，2010.

[12]王川杰，袁续祖，高威，等.威远气田页岩气井产量递减分析方法研究[J].天然气勘探与开发，2014，37（1）：55-59.