地震波形在致密砂岩储层孔隙度预测中的应用

王飞腾，王志章，赵永军，张静，赵凯，李汉林

（1.中国石油大学（华东）地球科学与技术学院，山东青岛　266580；2.中国石油大学（北京）地球科学学院，北京　102249）

地震波形在致密砂岩储层孔隙度预测中的应用

王飞腾1，王志章2，赵永军1，张静1，赵凯1，李汉林1

（1.中国石油大学（华东）地球科学与技术学院，山东青岛266580；2.中国石油大学（北京）地球科学学院，北京102249）

致密砂岩储层通常具有低孔、低渗、连通性差、非均质性强的特点，采用传统的波阻抗反演等方法研究，效果难以令人满意。为此，文中提出地震波形参数的概念，通过引入地震波形参数，对地震波的形态进行精细刻画；在此基础上，计算波形参数和孔隙度的相关系数，进而研究孔隙度与地震波形之间的关系；同时依据波形参数及BP神经网络算法进行孔隙度预测，为储层地震预测提供一种新的研究思路。

致密砂岩储层；地震波形参数；BP神经网络算法；孔隙度预测

地震波形作为地震勘探最主要的表现形式，蕴含着丰富的信息，也是最为复杂、最难解读的。前人对地震波形的研究主要集中在波形形状方面，即利用波形的几何属性来描述，取得了一定效果；同时，全波形研究也已展开，例如通过神经网络技术进行地震波形分类，从而进行地震相的研究［1-5］。在此基础上，对波形中蕴含的储层、孔隙流体等信息进行挖掘，将是下一步地震波形研究的一个重要方向。为此，本文引入了质心等7个参数刻画地震波形，进而研究孔隙度变化对地震波形的影响；同时，建立波形参数与孔隙度的相关模型，以实现对孔隙度的预测。经过实例验证，该方法预测符合率较高，应用效果较好。

1　方法原理

地震波穿过不同介质后波形会发生变化，研究变化后的地震波具有怎样的特征以及导致地震波形发生变化的地质因素，具有重要意义。单一的波形特征对比能够表明，不同的地震波波形的幅度均值、波形的宽窄、形态等具有差异。本文通过构造质心等7个参数来对地震波形进行定量准确刻画，并将波形参数与孔隙度进行相关分析，以研究孔隙度大小对地震波形态变化产生的影响，最终建立起波形参数与孔隙度的预测模型，实现对工区孔隙度的预测。

1.1地震波形参数提取

为了精细描述波形特征，构造了质心、均值、方差、均方根振幅、弧长、扭度、峰度等7个波形参数［6-9］。

1.1.1质心

质心（RM）即质量中心，是物质系统上被认为质量集中的一个假想点。该参数可以描述地震波各采样点的振幅在同一时窗内的几何关系。随着质心值增大，地震波波峰将有向下（采样点数值增大的方向）偏移的趋势。其表达式为

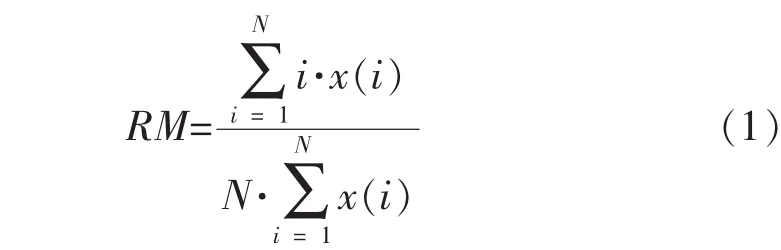
式中：x（i）为对应于点i的振幅值；N为时窗内的采样点个数。

1.1.2均值

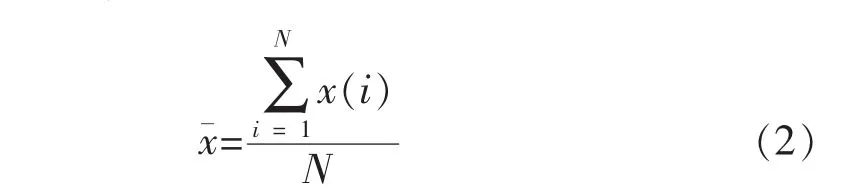
1.1.3方差

方差（S）是衡量总体中各变量间变异程度的统计量。该参数可以描述采样点的振幅偏离其均值的程度。随着方差增大，地震波的波动幅度将增大。其表达式为

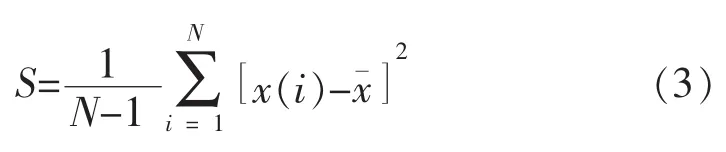
1.1.4均方根振幅

均方根振幅（RMS）是将振幅平方的平均值开平方得到的统计量。该参数对较大的振幅值非常敏感，可识别振幅异常。随着均方根振幅增大，地震波将整体向右（振幅值增大的方向）偏移。其表达式为

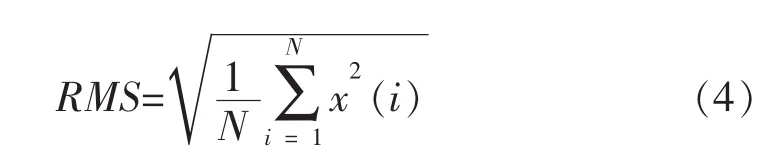
1.1.5弧长

弧长（L）是指单位时间内地震道的波形长度。该参数可以反映相邻采样点振幅值的变化程度。随着弧长值增大，地震波的波动幅度将增大。其表达式为

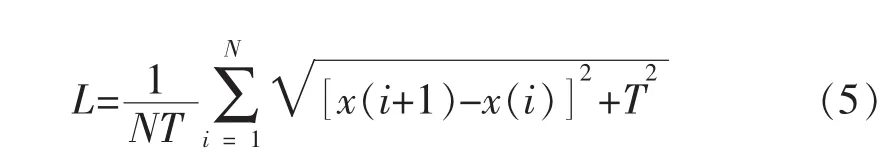
式中：T为采样周期。

1.1.6扭度

扭度（Vw）是一个量纲为1的量，用来评价分布函数相对均值的对称性。该参数主要用来反映地震波的偏度，当扭度值大于0，地震波将整体向右（振幅值增大的方向）偏移；当扭度值小于0，地震波将整体向左（振幅值减小的方向）偏移。其表达式为

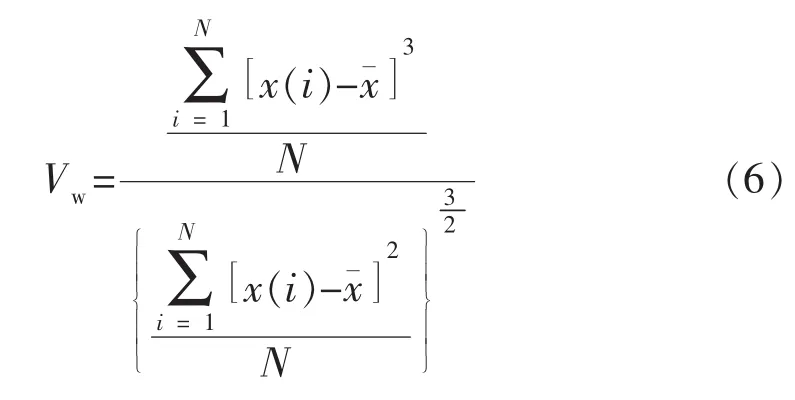
1.1.7峰度

峰度（Ku）是一个量纲为1的量，用来表征分布函数在均值附近的集中程度。峰度值越大，表示各采样点振幅值在均值附近的集中程度越高，地震波的波动幅度越小；峰度值越小，表示各采样点振幅值在均值附近的集中程度越低，地震波的波动幅度越大。其表达式为

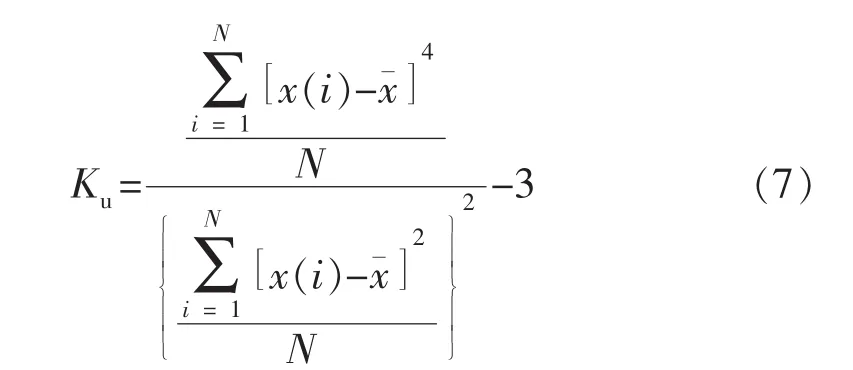
1.2数据标准化

波形参数的量纲不同，因此各种波形参数的数量级差别很大；如果直接使用原始数据，就会突出绝对值大的参数的作用，造成较大误差。在利用波形参数进行地质预测时，首先要消除各种波形参数和地质指标的量纲，把它们的原始数据变换为某种规范尺度下量纲为1的数据。

标准化的方式主要有极差正规化、极差标准化、标准差标准化、最大值标准化等［10-11］。本文采用的标准化方式为极差正规化。公式为

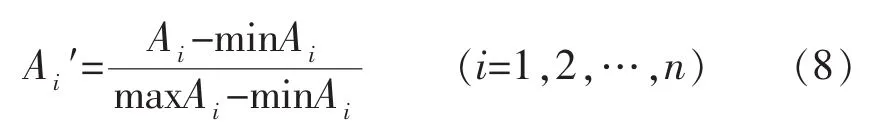
式中：Ai′为对原始数据进行标准化后的值（最小值为0，最大值为1）；Ai为波形参数或孔隙度的具体数值。

1.3孔隙度与地震波形的关系

将标准化之后的地震波形参数分别与孔隙度进行相关分析。选择相关性好的波形参数，根据其变化对地震波形态特征的影响，进而研究其与孔隙度的关系。

1.4孔隙度预测

单一的波形参数可以描述波形某些方面的特征变化，但如果要进行地质预测，需综合多个波形参数来建立模型。建模过程中，可以考虑多种数学方法。如果建立线性的预测方程，可以使用多元回归分析、逐步回归分析等方法；如果建立非线性的预测方程，可以使用神经网络、支持向量机、核岭函数等方法。本文采用逐步回归分析方法和神经网络方法分别进行地质预测，对比2种预测方法的误差，选择误差较小的方法进行实际应用。

1.4.1逐步回归分析方法

采用逐步回归分析方法建立预测方程时，可以优选出对预测指标作用大的自变量，同时可以在具有相关性的自变量之间进行筛选。该方法设定引入临界值和剔除临界值对自变量进行引入和剔除操作，直到既没有对y值（即预测指标）作用显著的变量可以引入回归方程，又没有作用不显著的变量可以从回归方程中剔除为止。

在具体操作中，将波形参数设为自变量，将孔隙度设为预测指标。逐步回归分析的流程如图1所示。

图1　逐步回归分析流程

1.4.2神经网络算法

神经网络算法是从生理的角度进行智能模拟，通过设置输入层、输出层、隐藏层以及激活函数来完成预测工作。神经网络算法按照学习的形式，可以分为有导师的学习和无导师的学习。其中，使用最广泛的是有导师学习形式中的BP神经网络算法［12-15］。本文的预测即采用该算法，该算法的核心是误差反向传播，即通过计算训练样本中理想输出和实际输出的差值，按照极小化误差理念来调整权矩阵，最终将训练结果应用于工作目标，实现地质预测。

2　应用实例

2.1研究区地质概况

大牛地气田位于鄂尔多斯盆地东北部，陕西和内蒙古交界处，面积2 003.714 km2，其具体构造位置在伊陕斜坡北部。区块内构造、断裂不发育，总体为北东高、西南低的平缓单斜，平均坡降6～9 m/km，倾角0.3～0.6°。局部发育鼻状隆起，未形成较大的构造圈闭。研究区X井区位于大牛地气田南部，面积160 km2，储层主要在下石盒子组、山西组、太原组。D66井区钻井揭露地层有第四系、白垩系、三叠系、二叠系、石炭系、奥陶系，钻井平均揭示地层厚度2 900 m。此次研究的目的层段为山西组山二段。该段储层岩性以中粗粒岩屑砂岩为主，中粗粒岩屑石英砂岩及石英砂岩次之；沉积相以三角洲相为主。

2.2孔隙度变化对地震波形的影响

提取研究区山二段的孔隙度与波形参数，分别进行标准化操作，得到研究区孔隙度与波形参数的关系及相关系数（见图2）。

由图2可以看出，均值、方差、均方根振幅、扭度和孔隙度的相关性较高，且均为正相关——表明孔隙度增大时，以上波形参数也会相应增加。根据上述研究可知，当孔隙度增大时，地震波将整体向右（振幅值增大的方向）发生偏移，且地震波的波动幅度增大。

2.3不同模型效果对比

2.3.1逐步回归方法模型建立

根据图2优选出均值、方差、均方根振幅、弧长、扭度5个波形参数进行逐步回归分析。经过逐步回归分析的筛选，优选出均值、方差、扭度3组参数，建立孔隙度（φ）预测方程：

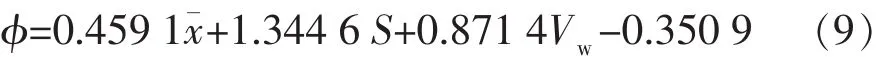
2.3.2BP神经网络算法模型建立

对提取的波形参数和孔隙度进行标准化，将7个波形参数设为输入层，将孔隙度设为输出层。通过调整阈值、学习率、隐藏层神经元的节点个数，将误差精度要求值不断降低，以达到最好的预测效果。网络训练完成后，利用建立好的BP神经网络模型完成预测。

2.3.3应用效果分析

将用于检测的孔隙度数据与采用2种方法所得的预测值进行对比。结果表明：采用逐步回归分析方法预测值平均绝对误差为1.37%，平均绝对百分误差为21.70%；采用神经网络算法预测值平均绝对误差为1.22%，平均绝对百分误差为19.30%。由此得出，采取神经网络算法进行地质预测效果更好。

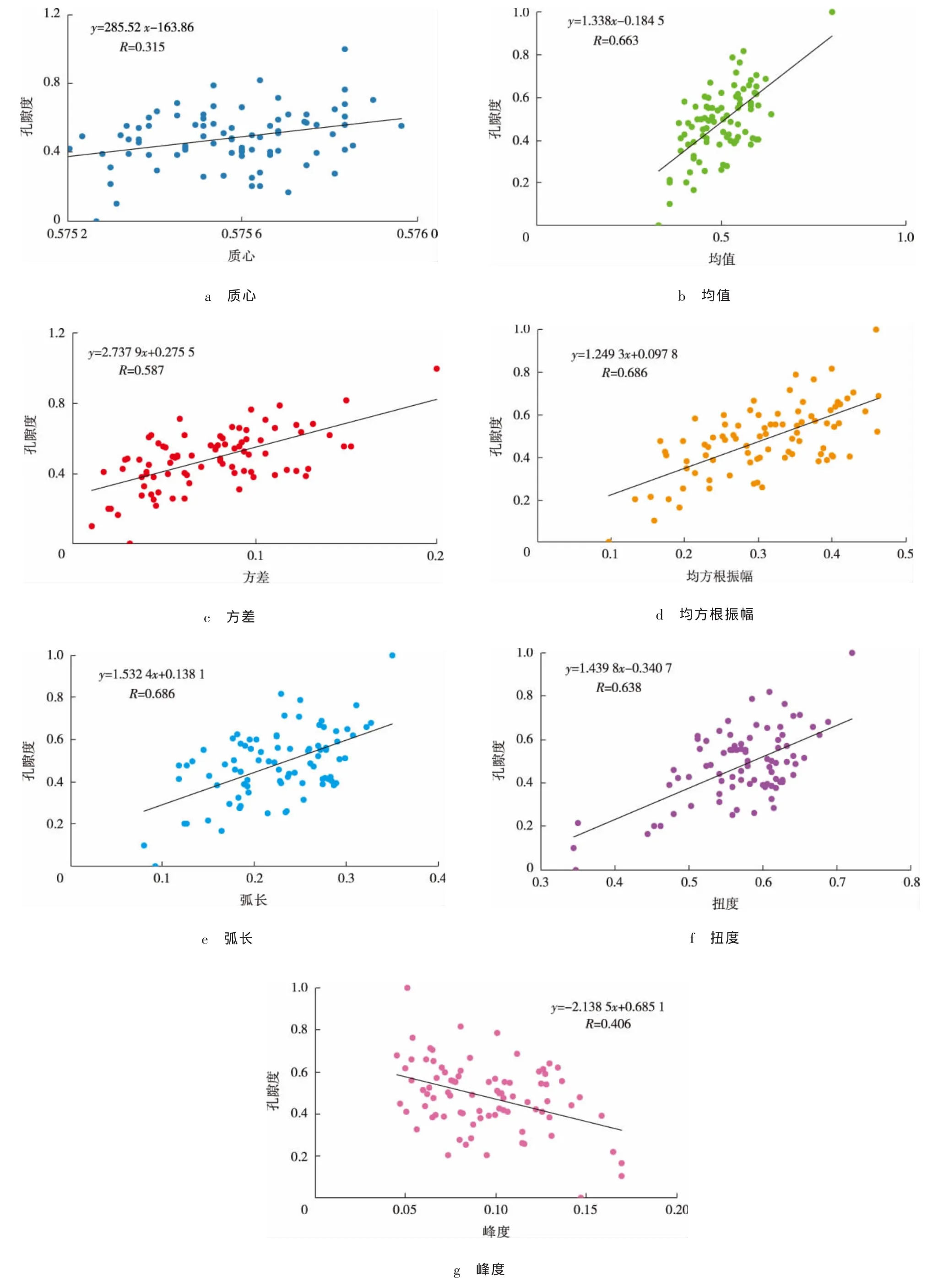
图2　山二段标准化后孔隙度与标准化后地震波形参数的关系

2.4 孔隙度预测

图3和图4分别为在波形参数约束下反演得到的孔隙度分布图和测井数据插值得到的孔隙度分布图［16-17］。对照两图可以看出，图3中的孔隙度在平面上变化更多，内容更丰富，井间储层变化刻画得更清楚，也更能精确反映出孔隙度在平面上的非均质性。因此，特别是对于大片的非井控区，前者得到的结果更具指导意义。

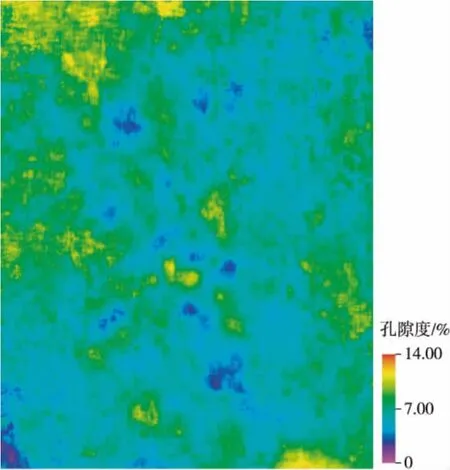
图3　利用波形参数预测的孔隙度分布

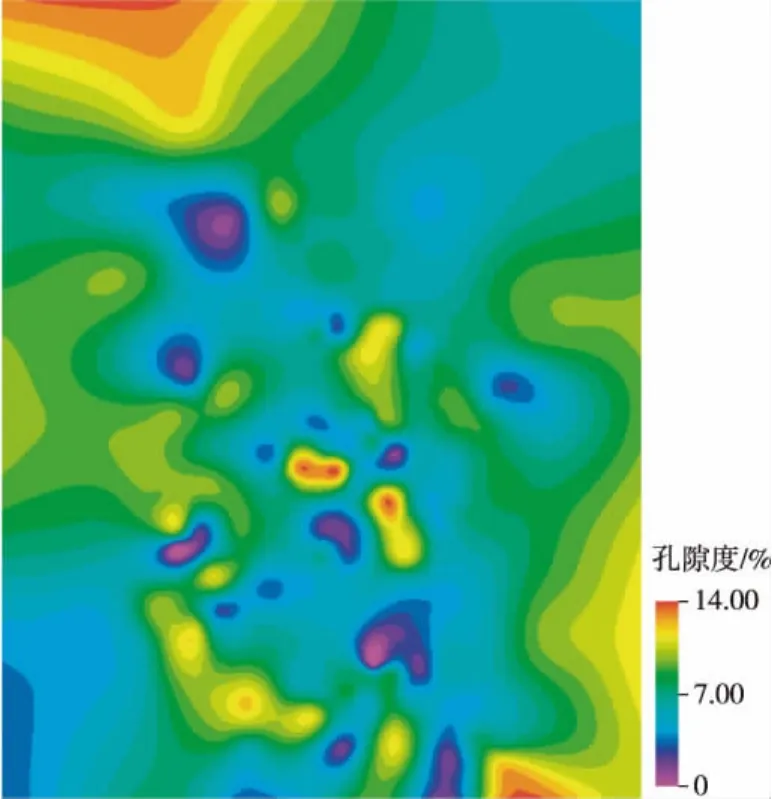
图4　利用测井数据预测的孔隙度分布

3　结论

1）利用波形参数能细致刻画地震波的形态变化。

2）孔隙度对于地震波形的影响，可以通过均值、方差、均方根振幅、扭度4个参数体现出来。当孔隙度增大时，地震波将整体向右（振幅值增大的方向）发生偏移，且地震波的波动幅度增大。

3）在致密砂岩的储层预测中，引入波形参数能够较好地提升预测效果。预测过程中，选用非线性的BP神经网络算法，效果要好于线性的逐步回归分析算法。

［1］Litvinov A Y.Reservoir characterization from seismic waveform using forward modeling and pattern recognition［J］.The Leading Edge，2002，21（10）：1028-1031.

［2］师永民，祁军，张成学，等.应用地震波形分析技术预测裂缝的方法探讨［J］.石油物探，2005，44（2）：128-130.

［3］邓传伟.利用波形建立地震相［J］.石油地球物理勘探，2004，39（5）：539-542.

［4］江青春，汪海，李丹，等.地震波形分类技术应用条件及其在葡北地区沉积微相研究中的应用［J］.石油与天然气地质，2012，33（1）：135-140.

［5］李强，戴鸿鸣.地震波形分类技术在红浅一井区的应用［J］.断块油气田，2007，14（1）：14-15.

［6］张文旗，王志章，韩海英，等.波形差异分析技术在气田高产气区预测中的应用［J］.科技导报，2011，29（18）：29-32.

［7］王志章，韩海英.现代油藏描述关键技术［J］.地学前缘，2011，18（5）：296-302.

［8］闫安菊，阎建国.波形与振幅属性在储层预测中的敏感性探讨［D］.成都：成都理工大学，2013.

［9］伍新和，林良彪，张玺华.地震波形分析技术在川西新场地区沉积微相研究中的应用［J］.成都理工大学学报：自然科学版，2013，40（4）：400-416.

［10］郭刚明，颜其彬.地震属性技术的研究与应用：以潍北凹陷灶户构造为例［D］.成都：西南石油大学，2005.

［11］陈东，王彦春.地震多属性分析及其在储层预测中的应用研究［D］.北京：中国地质大学（北京），2008.

［12］徐振东，李颖.人工神经网络的数学模型建立及成矿预测BP网络的实现［D］.长春：吉林大学，2004.

［13］张治国，杨毅恒.人工神经网络及其在地学中的应用研究［D］.长春：吉林大学，2006.

［14］李东安，宁俊瑞，刘振峰.用神经网络和地质统计学综合多元信息进行储层预测［J］.石油与天然气地质，2010，31（4）：493-498.

［15］李汉林，赵永军，王海起.石油数学地质［M］.东营：中国石油大学出版社，2008：161-176.

［16］王波.测井约束地震反演技术分析及其应用［J］.断块油气田，2006，13（5）：23-24.

［17］何英伟.地震重构反演在大庆长垣剩余油预测中的应用［J］.断块油气田，2013，20（2）：162-165.

（编辑李宗华）

Porosity prediction for tight sandstone reservoir by seismic waveform

Wang Feiteng1，Wang Zhizhang2，Zhao Yongjun1，Zhang Jing1，Zhao Kai1，Li Hanlin1
（1.College of Geosciences and Technology，China University of Petroleum，Qingdao 266580，China；2.College of Geosciences，China University of Petroleum，Beijing 102249，China）

With characteristics of low porosity，low permeability，poor connectivity and serious heterogeneity of tight sandstone reservoirs，the porosity result isn′t satisfactory by using wave impedance inversion method.Therefore，the concept of seismic waveform parameters is proposed in this article for accurate description of seismic waveform.Calculating the correlation coefficient between waveform parameters and porosity，the relationship between porosity and the seismic waveform is studied.Porosity based on BP neural network algorithm and seismic waveform parameters is predicted simultaneously，which provides a new way for reservoir prediction.

tight sandstone reservoir；seismic wave parameters；BP neural network algorithm；prediction of porosity

“十二五”国家油气重大专项“鄂尔多斯盆地大牛地致密低渗气田开发示范工程”（2008ZX05045）

TE132.1+4；P631

A

10.6056/dkyqt201504005

2014-11-07；改回日期：2015-03-13。

王飞腾，男，1990年生，地质资源与地质工程专业在读硕士研究生，研究方向为油气藏开发地质。E-mail：wangfeiteng90 @163.com。引用格式：王飞腾，王志章，赵永军，等.地震波形在致密砂岩储层孔隙度预测中的应用［J］.断块油气田，2015，22（4）：430-434.

Wang Feiteng，Wang Zhizhang，Zhao Yongjun，et al.Porosity prediction for tight sandstone reservoir by seismic waveform［J］.Fault-Block

Oil&Gas Field，2015，22（4）：430-434.