基于新模型低渗透油藏产能研究

刘海龙，吴淑红，王冠，李华，李春涛

（1.中国石油勘探开发研究院，北京100083；2.提高石油采收率国家重点实验室，北京100083；3.中国地质大学（北京）能源学院，北京100083；4.中国石油新疆油田公司勘探开发研究院，新疆 克拉玛依 834000）

0 引言

目前我国许多油田已经进入高含水期，而且处于低渗透油藏开采阶段，前人虽然对低渗透油藏做过很多研究，但主要集中于该类油藏储层特征描述[1]、油田注水方案设计[2]、井位部署方案设计[3]等方面，对于其压力传播规律的研究还很欠缺 （前人的研究主要是基于一维径向渗流[4]、定产量生产条件[5]或是拟启动压力梯度模型）。然而，在油田实际开发过程中，往往存在边界定压（如注水）生产情况，且对于渗流室内试验及大型行列排状注水，经常存在一维单向流动，采用拟启动压力梯度模型并不能真正反映带状低渗透油藏实际流体的渗流特征。因此，有必要建立更能反映低渗透油藏真实流体渗流特征的模型。

1 新渗流模型建立

非线性渗流的数学模型描述方法很多[6-8]，但目前的数学模型还是存在一定的缺陷。例如：在拟启动压力模型中，当压力梯度低于启动压力梯度时，拟启动压力梯度模型就不能计算出流体的渗流速度；幂指数模型在模拟线性段时误差比较大；全程描述模型很难求解出线性区与非线性区连接位置的渗流速度；三参数连续模型无法反映实际渗流存在启动压力现象；两参数连续模型无法表现渗流曲线突变信息。因此，有必要推导新的模型。

若假设理想的孔隙介质，其单位截面积中有n根半径为r的毛细管，且其几何尺寸、流体性质、压差均与真实岩石相同，若流体通过岩石孔道的实际长度与岩石外表长度之比为σ，岩石截面积为A。按照泊稷叶公式（对理想岩石）可导出公式：

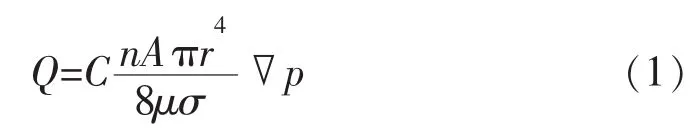
式中：Q为通过毛细管的总流量，cm3/s；C为单位换算系数，达西制单位下 C 为 1；μ 为黏度，mPa·s；▽p为流体压力梯度，MPa/m。

低渗透油藏孔喉半径微小，小到微米级别，已经不能忽略吸附边界层的影响 （孔隙流体在岩石固体表面发生吸附，减小了可流动面积）。吸附边界层导致储层流体不均匀分布，距离固体边界越近，流体受影响程度越大，流动性越低。边界层厚度随着驱替压差的升高而变薄，可流动流体比例增加，但流体黏度变大，需要克服更大的流体屈服应力值。这样导致可流动流体性质发生改变，渗流横截面积也发生相应改变，因而，低渗透油藏不再遵循达西定律，表现出非线性渗流的特征。考虑边界层影响和流体屈服应力，将式（1）修正为

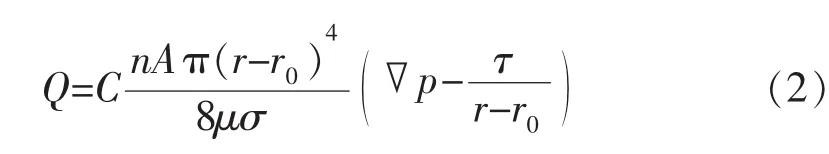
式中：r0为边界层厚度，m；τ为流体屈服应力，MPa。

该模型中毛细管的孔隙度、渗透率分别为

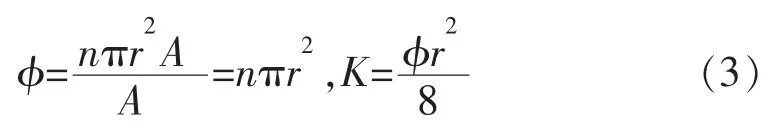
徐绍良等[9]通过非线性流体室内实验指出，同一根毛细管，边界层厚度与压力梯度呈负相关，同一流体的屈服应力可视为常数，即

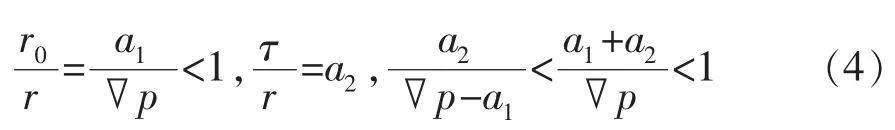
式中：a1，a2分别为与油藏物性相关的实验参数。

联立式（1）-（4），并整理得（忽略高阶无穷小）

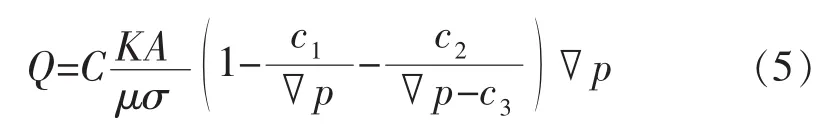
式中：c1，c2，c3分别为与油藏物性相关的实验参数。

当 c1＝c2＝0 时，式（5）为达西模型；当 c1≠0，c2＝0时，式（5）为拟启动压力梯度模型；当 c1＝0，c2≠0 时，式（5）为两参数连续模型；当 c1≠0，c2≠0 时，式（5）为三参数连续模型。由此可知：式（5）很好地诠释了低渗透油藏非线性渗流特征。

从新模型建立过程可知：c1主要体现储层流体渗流需要克服屈服应力，c2主要体现吸附边界层对储层流体的影响。由于储层流体渗流通道的尺寸微小，必须考虑微尺度效应。屈服应力、吸附边界层、微尺度效应不是单独存在的，而是相互影响、相互耦合。由于微尺度效应的存在，使得表面力的影响超过了体积力，成为支配作用力。表面力越大，储层流体受吸附边界层的束缚越强，使得储层流体表现出更强的非牛顿性，导致储层流体表现为非线性渗流特征，偏离达西定律。此外，束缚作用力越强，抵消驱替力就越多，则储层流体更容易被边界层吸附。加大边界层的厚度，加剧微尺度效应，系数c3很好地体现了相互耦合、相互影响的效应。

由于低渗透油藏储层的多孔介质渗透率是随驱替压力变化而变化的，可将视为渗透率的修正系数；低渗透油藏储层流体中存在的屈服应力和吸附边界层是启动压力梯度存在的本质，两者相互作用，导致启动压力梯度随驱替压力梯度变化而变化；式（5）中的在数值上与启动压力值相等，相当于拟启动压力梯度模型的启动压力梯度相，间接说明了启动压力梯度存在的本质原因。此外，令式（5）中的Q=0，可求出低渗透油藏储层真实的启动压力梯度， 即。综上所述，新模型是合理的。

2 产能模型建立

2.1 模型描述

低渗透油藏往往存在一维单向流动，对于一维单向流动，主要有平面线性流和平面径向流，当对低渗透油藏开展渗流室内试验，或者进行大型行列排状注水开发时，对于地下流体渗流的描述显得尤为重要。低渗透油藏一维渗流物理模型如图1所示，地层流体微可压缩，h为油藏平均厚度，m；w为宽度，m；L为长度，m；pe为原始地层压力，MPa；pwf为井底流压，MPa。地层左端具有供给边缘，右端为一直线排液通道，一口生产井位于右端排液通道处，该井以外边界定压、内边界定产进行生产。

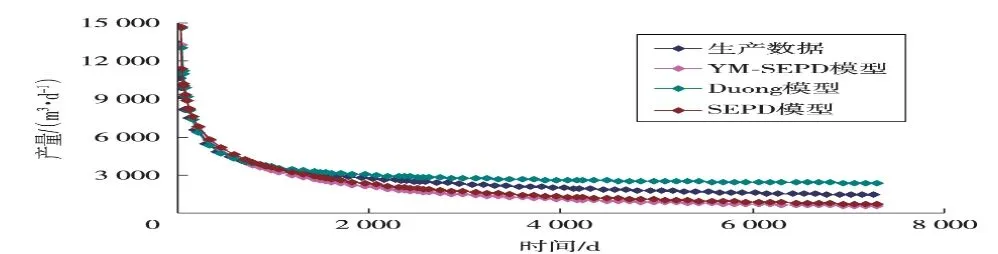
图1 低渗透油藏一维渗流物理模型

2.2 压敏效应描述

采用Yilmazo和NurA共同提出的渗透率模量模型，来描述压力敏感效应，即

式中：α 为压力敏感系数，MPa-1；p 为地层压力，MPa；K，Ki分别为地层渗透率和地层初始渗透率，10-3μm2。

式（6）并不能真实地反映岩石本身对孔隙压力的影响，在实际的开发过程中，低渗透油藏表现出的是岩石本身对孔隙压力的敏感性[10]。为更好地描述压力敏感效应，引入岩石本体有效应力[11]：

应用式（7），可将内外应力相互转换，用内应力敏感指数来表示压力敏感效益。岩石变形遵循孔隙度不变的原则。因此，式（8）可修正为

2.3 低渗透油藏产能模型建立

基于新模型考虑压敏效应的低渗透油藏非线性渗流运动方程为

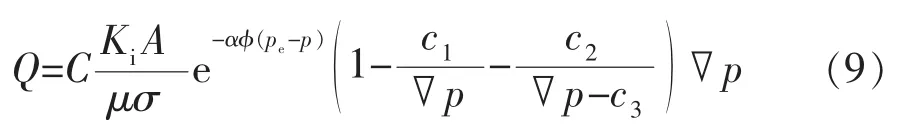
初始条件为

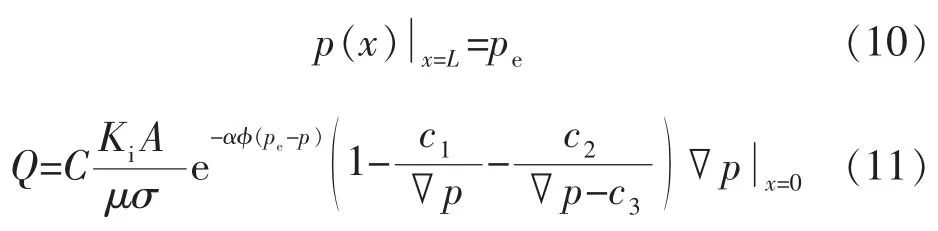
求解式（9）并积分得

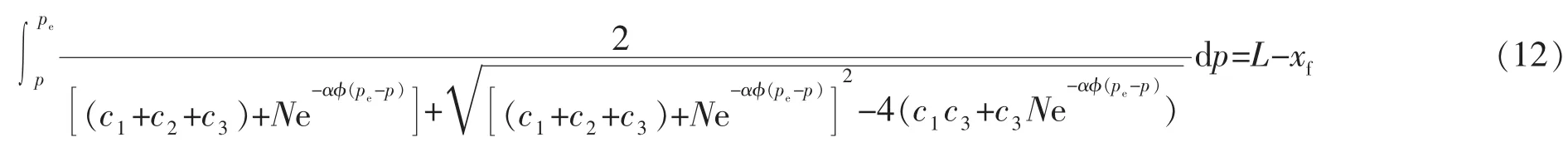
式中：xf为水驱前沿位置，m。

当不考虑压敏效应时，即α=0，由式（12）可得

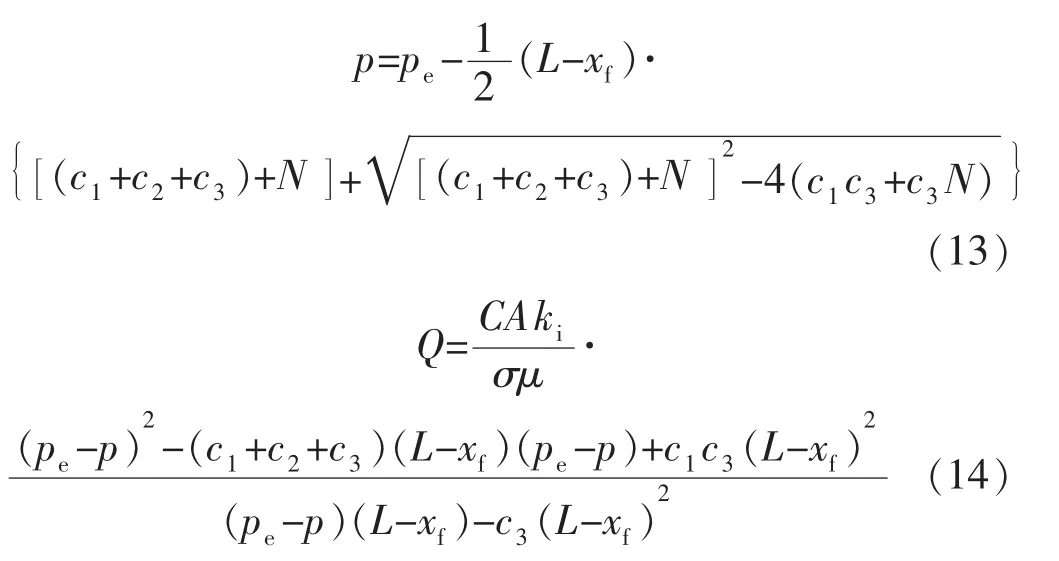
当不考虑压敏效应和边界层影响时，即α=0，c2=0时，由式（12）可得

当不考虑压敏效应、边界层、屈服应力影响时，即α=0，c1=c2=0，由式（12）可得

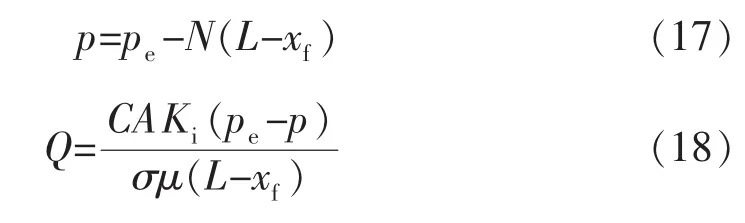
式 （16）为考虑启动压力梯度的线性渗流产能公式，式（18）为常规油藏的线性渗流产能公式[12]，二者均可间接证明式（12）的正确性。由于式（12）比较复杂，是一个关于Q的超越方程f（Q）=0，采用近似的牛顿迭代对该方程进行数值求解，并构造以下迭代：

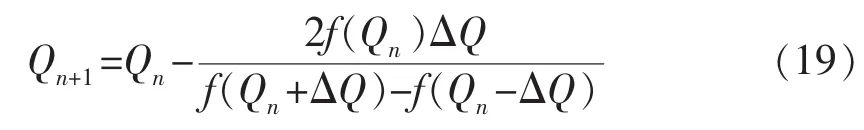
式中：Qn，Qn+1分别为 n，n+1 时刻的产量，m3/d；ΔQ 为产量步长，m3/d。

3 产能影响因素分析

取低渗透油藏井底压力为10 MPa，原始地层压力为 30 MPa，孔隙度为 10.1%，原油黏度为 2.4 mPa·s，原始地层压力下渗透率为3.22×10-3μm2，油藏长度、宽度、厚度分别为100，50，10 m，压力敏感系数为0.01 MPa-1，流量为5 m3/d。将实验室测得的比例参数换算为新模型的 3个系数，其值分别为 0.070 3，0.050 1，-0.096 8 MPa/m，测得的真实启动压力梯度为0.093 7 MPa/m。采用控制变量方法，分别分析非线性新模型的3个系数、水驱前缘位置、压力敏感系数、真实启动压力梯度等因数对低渗透油藏产能的影响。

3.1 非线性新模型系数

非线性新模型3个系数对产能的影响见图2。单从数值上看，产能随着c1，c2，c3的增加而增加，但三者是相互影响的。研究发现：随着三者之和的增加，产能降低。因为微尺度效应、吸附边界层和屈服应力三者是一个耦合的效应，耦合效应的增加，对流体阻碍能力就越强，流体需要更多的能量克服阻力做功，因而被驱替出孔隙到达井底的流体就减小，相应地流量就变小，产能降低。

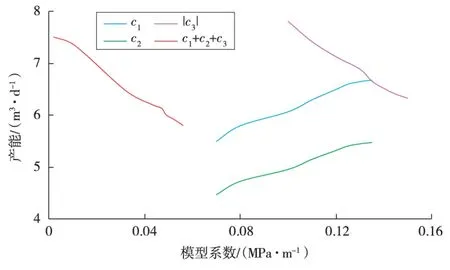
图2 非线性新模型系数对产能的影响

3.2 水驱前缘位置

水驱前缘位置对产能的影响比较明显 （见图3）。当生产压差为20 MPa时，随着水驱前缘位置从20 m增大到80 m，产能从4.36 m3/d升高到9.78 m3/d，产能增加一倍多。对于定边界压力的低渗透油藏，相同距离的压力梯度是一样的，水驱前缘位置越大，说明压力传播得越快，压力波及范围越大，压力激动区的面积就越大，同一时刻被驱替出孔隙的原油就越多。这表现出井底流量增加，产能增加。但并不是一有生产压差就有产能，只有当生产压差达到一定值时，才会有产能。这间接说明低渗透油藏非线性渗流不在遵循达西定律，流体流动必须克服一定的储层阻力。

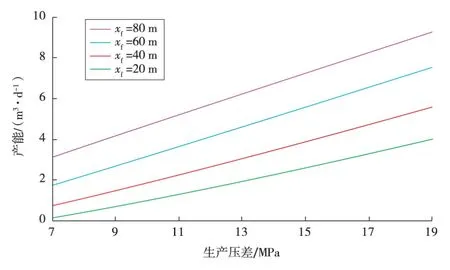
图3 水驱前缘位置对产能的影响

3.3 压力敏感系数

压力敏感系数对产能影响比较明显（见图4）。当生产压差为20 MPa时，随着压力敏感系数从0.01 MPa-1增大到0.09 MPa-1，产能从8.61 m3/d降到7.12 m3/d。对于同一压力敏感系数下，当生产压差从7 MPa增加到11 MPa时，产能近似线性增加；生产压差超过11 MPa时，产能增加缓慢，且渗透率与压力为负相关关系。当压力增加到一定值时，压敏效应更为明显，储层渗透率下降得越快，则孔隙之间的连通性相对变差，流体流动性降低。因此，并不是生产压差越大越好，而是在一定范围内放大生产压差，产能增加较大。

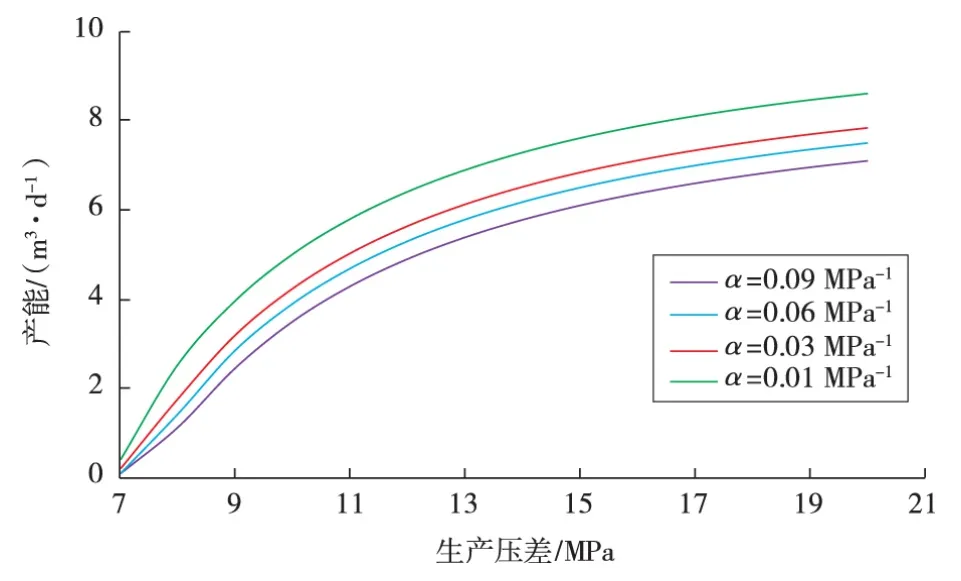
图4 压力敏感系数对产能的影响

3.4 真实启动压力梯度

将真实启动压力梯度用G代替，得到真实启动压力梯度对产能的影响（见图5）。同一生产压差下，随着真实启动压力梯度的增加，产能逐渐降低。当生产压差为20 MPa时，真实启动压力梯度从0.03 MPa/m增加到0.06 MPa/m，产能从 8.84 m3/d降到 8.61 m3/d，因而真实启动压力梯度对产能的影响不大。

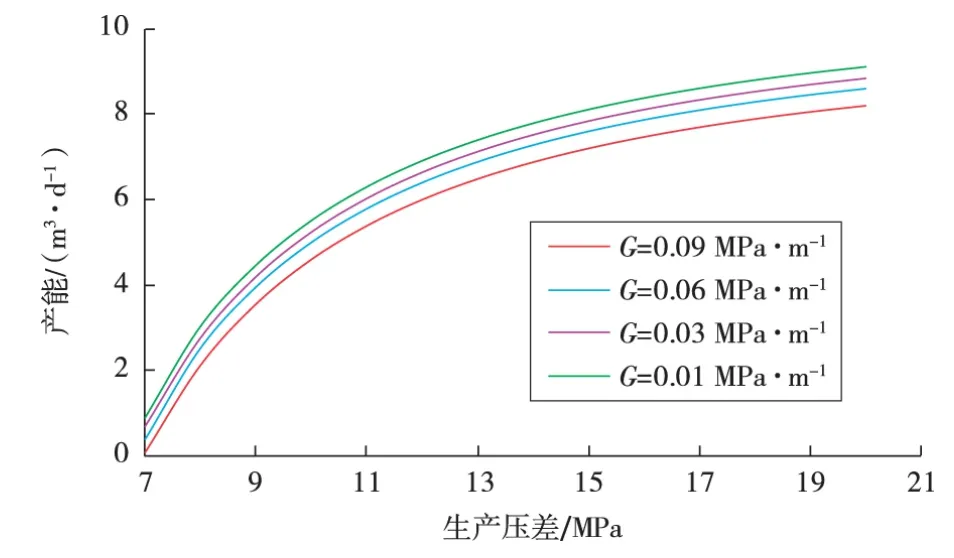
图5 启动压力梯度对产能的影响

提高产能可借助外来能量来补充地层能量的不足，如注水或注气，从而提高储层孔隙流体压力，减小或消除启动压力梯度的影响。采用压裂改造低渗透储层，在储层中建立“流动网络”，连通储层更多的渗流通道，增大储层暴露的渗流面积，加上外部注水或注气，提前补充地层能量，增加储层压力，减小储层流体渗流阻力，使得启动压力梯度减小或“消失”。

4 结论

1）基于新模型，考虑压力敏感效应、启动压力梯度的影响，建立了一种适用于定压边界的低渗透油藏直井产能评价数值模型。

2）新的渗流模型系数对产能影响较小，产能随着系数和的增大而降低。

3）水驱前缘位置对产能的影响比较明显，随着水驱前缘位置的增大，产能提高很快。水驱前缘位置对产能的影响受生产压差的控制，同一水驱前缘位置下，产能与生产压差近似为线性正相关关系。

4）压力敏感系数对产能的影响较大。在低渗透油藏开发中，保持适当的生产压差，减小渗透率对压力的敏感，有助于提高单井产能。

5）真实启动压力梯度对产能的影响较小，真实启动压力梯度越小，产能越高。采用压裂或超前注水，可较小或“消除”储层启动压力梯度的影响。

[1]刘睿，姜汉桥，陈民峰，等.江苏油田复杂小断块油藏分类[J].新疆石油地质，2009，30（6）：680-682.

[2]王哲.断块油藏注采井部署优化研究[D].青岛：中国石油大学（华东），2008.

[3]赵梓平，朱宏绶.苏北条带状中低渗油藏注水开发政策研究：以台兴油田为例[J].内蒙古石油化工，2011，37（8）：217-219.

[4]齐亚东，雷群，杨正明，等.条带状特低渗透断块油藏布井方案评价与优选[J].石油钻采工艺，2011，33（4）：66-70.

[5]何军，胡永乐，何东博，等.低渗致密气藏产能预测方法[J].断块油气田，2013，20（3）：334-336，358.

[6]时贤，程远方，李友志，等.致密气藏压裂井产能预测方法研究[J].断块油气田，2013，20（5）：634-638.

[7]蒋瑞忠，杨仁锋.低渗透油藏非线性渗流理论与数值模拟技术[M].北京：石油工业出版社，2010：26-31.

[8]李松泉，程林松，李秀生，等.特低渗透油藏非线性渗流模型[J].石油勘探与开发，2008，35（5）：606-612.

[9]徐绍良，岳湘安.低速非线性流动特性的实验研究[J].中国石油大学学报：自然科学版，2007，31（5）： 60-63.

[10]李传亮.储层岩石的应力敏感性评价方法[J].大庆石油地质与开发，2006，25（1）：40-42.

[11]李传亮，孔祥言，徐献芝，等.多孔介质的双重有效应力[J].自然杂志， 1999，21（5）：288-292.

[12]王晓冬.渗流力学基础[M].北京：中国地质大学出版社，2006：41-56.