计及潮流断面稳定限额的分区电网最大供电能力研究

刘盛松，秦旭东，汪志成，胡 伟

(江苏省电力公司调度控制中心，江苏南京210024)

随着我国经济的快速发展，用电负荷逐年攀升，同时，为了适应不断增长的用电需求，电网规模也不断扩大。以江苏电网为例，至2014年年底，电网装机容量突破80 000MW，220 kV及以上的输电线路总长度超过36 000 km，220 kV及以上的变电容量超过 26 000万kV·A，已发展成为较大规模电网。

合理的电网结构，应满足分层分区的原则[1]。合理分区，以受端系统为核心，将外部电源连接到受端系统，形成一个供需基本平衡的区域，并经联络线与相邻区域相连。随着高一级电压电网的建设，下级电网应逐步实现分区运行，相邻分区之间互为备用。江苏电网已形成以500 kV电网为骨干网架，220 kV电网分区运行的格局。科学合理地评估分区电网最大供电能力对于电网规划与运行具有巨大的经济价值和现实意义。一方面研究TSC可以指导电网规划部门正确评价分区电网现状，分析制约分区电网供电能力的薄弱环节，通过进一步优化现有网架结构，挖掘已有电网在更高负载水平下运行的巨大潜力；另一方面，研究TSC可以为电网运行部门提供分区电网的供电裕度，为能否安排某一项电气设备检修提供依据，有利于科学地制定用电负荷高峰时段有序用电方案，确保电网运行的安全性与可靠性。

近年来，配电网的TSC研究[2-5]逐渐引起人们广泛的关注，但作为电网运行的重要指标—分区电网TSC却少有文献论及。目前，实际应用中采取的方法为尝试近似法，即采用人工方法在分区电网现有负荷水平下逐次增加用电负荷，通过反复的潮流计算，逼近电网安全运行的极限，此时的用电负荷水平即为分区电网的TSC。人工方法不仅计算繁琐，而且考虑的电网安全运行约束条件有限。本文建立了分区电网的TSC非线性最优化模型，将TSC作为目标函数，广义参数化潮流方程作为等式约束条件，发电机、输电线路、变压器的安全运行作为不等式约束条件，同时约束条件还将关键输电断面稳定限额引入，间接在TSC中考虑了分区电网的N-1/N-2约束，TSC计算模型更加符合电网运行实际，采用非线性内点法求解。

1 分区电网的TSC概念

分区电网通常由高一电压等级主网与分区电网之间的联络变（受电通道）、分区内发电机组、输电线路、用电负荷构成。江苏苏州地区220 kV分区电网示意图如图1所示，每1个220 kV分区电网通过1座及以上500 kV变电站、2台及以上500 kV主变受电。

图1 苏州地区220 kV分区电网示意图

分区电网TSC可以描述为：在满足分区电网安全运行准则条件下，分区内最大负荷供应能力。

通过分区电网的构成可以定性地分析：TSC受分区内发电机组出力、输电线路输送能力、通过与高一电压等级主网的联络变的受电能力等因素影响。

2 基于最优潮流的TSC数学模型

最优潮流问题[6-10]数学上可描述为：在网络结构和参数给定的条件下，确定系统的控制变量，使得描述系统运行效益的某一给定的目标函数取得最优，同时满足系统的运行和安全约束。

可以用简洁的数学形式描述为：

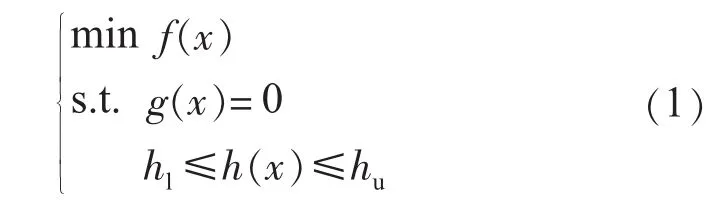
式（1）中：x 包括系统控制变量和状态变量，f（x）为标量目标函数；g（x）为潮流方程等式约束；h（x）为不等式约束，分为变量不等式和函数不等式，常为系统的安全约束和元件的运行限值约束。

2.1 目标函数

考虑分区电网TSC的最优潮流目标函数则可以写为：

式（2）为分区电网最大负荷供应能力。

2.2 等式约束

等式约束为广义参数化潮流方程，分别为：

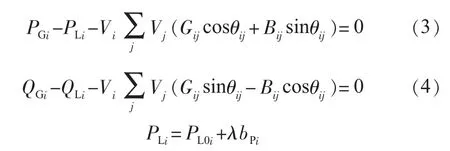
QLi按恒功率因数随变化

2.3 常规不等式约束

常规不等式约束包括发电机有功功率约束、无功功率约束、节点电压幅值约束、输电线路载流量约束，分别为：

2.4 关键输电断面稳定限额约束

输电断面是由电网中有功潮流流向一致的线路、变压器构成的，常见的形式有若干线路、变压器或由二者共同构成的。关键输电断面是结合电网实际运行情况选择与制定的，是实现对复杂电网的降维控制。断面限额的编制依据是《电力系统安全稳定导则》以及相关安全稳定计算管理规定，稳定限额确定原则是考虑电网N-1、N-2、直流闭锁等故障形式后电网能够保持静态稳定、暂态稳定与动态稳定。因此，关键输电断面已成为大电网的重要安全特征，调度运行中需严格控制关键输电断面潮流在稳定限额以内，确保电网安全稳定运行。关键输电断面稳定限额约束定义为：

在分区电网TSC数学模型中考虑关键输电断面稳定限额约束，更加符合电网实际运行的需要，具有现实意义。

3 非线性内点法

基于最优潮流的TSC数学模型式（1）包含大量的等式和不等式约束，可以采用非线性内点法[11，12]求解。内点法是Lagrangian函数、牛顿方法和对数障碍函数三者的结合，其对不等式约束的处理能力较强，不需要识别起作用约束集，这是内点法的一个较大的优势，同时具有对问题规模不敏感的优点。非线性原—对偶内点法如下：

对于数学模型式（1），引入松弛向量 sl和 su，sl≥0，su≥0，式（1）重新写为：

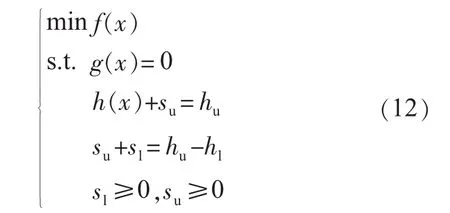
引入对数障碍函数至目标函数，可以消去松弛变量的非负性约束，式（1）又可转化为如下形式：

式（13）中：m为不等式约束的个数。引入Lagrangian乘子向量 λ，v，π，形成 Lagrangian 函数：

式（14）中：障碍参数μ＞0，随着算法迭代过程的进行，逐渐趋近于0。

根据Kuhn-Tucker最优性一阶必要条件，得到：

Kuhn-Tucker条件式（15）又可转化为如下形式：

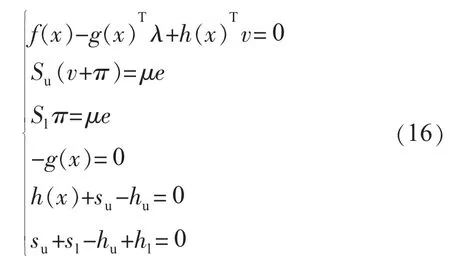
式（17）中：αk为原变量和对偶变量的步长。

搜索方向可由求解下列系统方程得到：

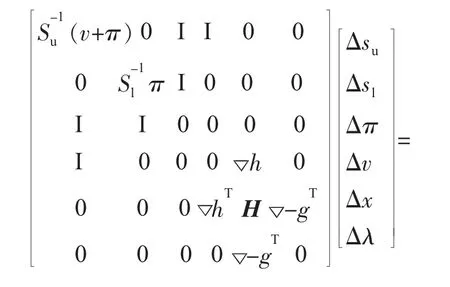
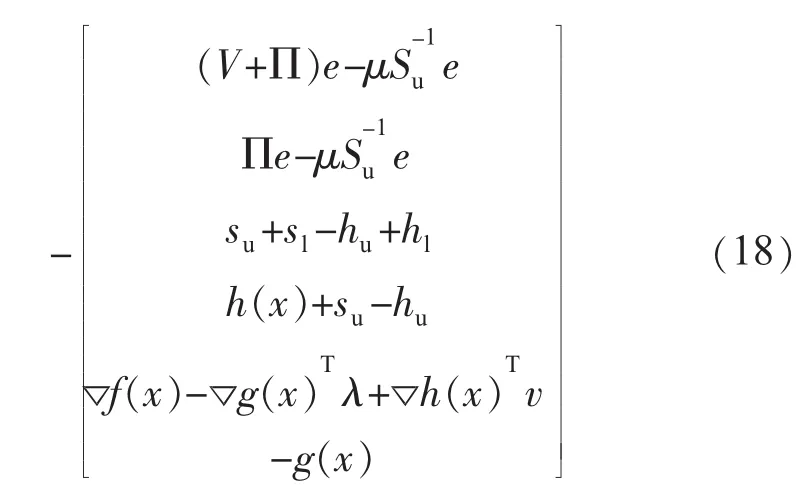
式 （18）中：H为Lagrangian函数的Hessian矩阵；V=

系统方程 （18）的获得，是由New ton方法求解Kuhn-Tucker最优性条件式（16）得出。为确保新的迭代点严格的正定，原对偶变量的步长可由下式确定：

如果第k次迭代满足如下收敛判据，则迭代结束。

式（20）中：ε1和 ε2为给定的收敛判据；gap为互补间隙。

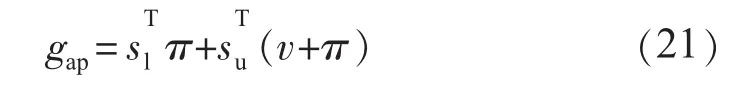
式（21）中：dobj为对偶目标函数值。

如果第k次迭代不满足收敛判据式（20），则修正障碍参数μ：

式（23）中：n为系统控制变量和状态变量的个数。重复上述迭代过程直至满足收敛判据。

4 算例分析

以某年度江苏电网为例，选取了3个典型220 kV分区电网—车坊分区、东龙分区、徐宿分区，对提出的基于最优潮流的分区电网最大供电能力计算方法进行了验证。

4.1 单座500 kV变电站受电的220 kV分区电网

220 kV车坊分区示意图如图2所示。车坊分区电网规模及关键输电断面稳定限额分别如表1、表2所示。车坊分区TSC和相关约束条件值如表3所示。

由表3可见，500 kV主变受电能力尚有一定裕度，但分区内机组出力已满发，220 kV车坊—南施/星港双线潮流达到稳定限额，这2个因素成为制约TSC进一步提高的因素，对电网规划与调度运行人员具有重要的指导意义。

图2 车坊分区

表1 车坊分区电网规模

表2 车坊分区关键输电断面稳定限额

表3 车坊分区TSC及相关约束信息

4.2 2座500 kV变电站受电的220 kV分区电网

220 kV东龙分区示意图如图3所示。

图3 东龙分区

东龙分区电网规模及关键输电断面稳定限额分别如表4、表5所示。东龙分区TSC相关的信息如表6所示。

表4 东龙分区电网规模

由表6可见，TSC达到最大值时，500 kV东善桥主变、220 kV晓庄—下关/中央门双线达到稳定限额，但分区内机组出力尚有611MW未予释放，说明220 kV晓庄—下关/中央门双线成为电力输送瓶颈，制约了TSC。

表5 东龙分区关键输电断面稳定限额

表6 东龙分区TSC及相关约束信息

4.3 3座500 kV变电站受电的220 kV分区电网

220 kV徐宿分区示意图如图4所示。徐宿分区电网规模及关键输电断面稳定限额分别如表7、表8所示。徐宿分区的TSC相关信息如表9所示。

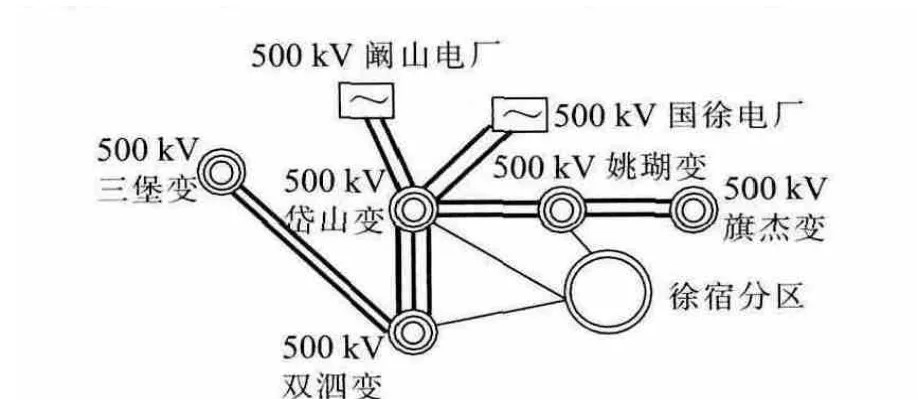
图4 徐宿分区

表7 徐宿分区电网规模

表8 徐宿分区关键输电断面稳定限额

表9 徐宿分区TSC及相关约束信息

该分区500 kV主变受电能力尚有较大裕度，机组出力已达限值，220 kV双泗—南蔡三线潮流达到稳定限额，制约了分区电力的进一步受进，是TSC的主要影响因素。

5 结束语

本文基于最优潮流，提出了分区电网最大供电能力计算方法。将TSC转化为满足电网安全运行约束条件下的最优化问题，约束条件中考虑了关键输电断面稳定限额，在对约束条件降维处理的同时计及了电网的N-1/N-2约束，由非线性内点法求得TSC。江苏电网3个典型220 kV分区电网算例的计算结果表明，采用的TSC计算方法能够满足电网规划与运行的要求，具有较高的适用性和实际应用价值。

[1]DL/T 755—2001，电力系统安全稳定导则[S].

[2]肖 峻，张 婷，张 跃，等.基于最大供电能力的配电网规划理念与方法[J].中国电机工程学报，2013，33(10)：106-113.

[3]肖 峻，刘世嵩，李振生，等.基于潮流计算的配电网最大供电能力模型[J].中国电机工程学报，2014，34(31)：5516-5524.

[4]肖 峻，郭晓丹，王成山，等.配电网最大供电能力模型解的性质[J].电力系统自动化，2013，37(16)：59-65.

[5]肖 峻，李振生，刘世嵩，等.电压约束及网损对配电网最大供电能力计算的影响[J].电力系统自动化，2014，38(5)：36-43.

[6]刘雪连，段振刚，王 坚，等.考虑电压安全裕度的多目标最优潮流模糊建模[J].电网技术，2011，35(12)：112-117.

[7]杨 伟，滕百岸，孙 磊.电力市场中最优潮流模型及算法研究[J].电网技术，2012，36(2)：126-130.

[8]季 聪，卫志农，汤 涌，等.基于自动微分技术的VSC-HVDC内点法最优潮流[J].电网技术，2012，36(10)：184-189.

[9]李静文，赵晋泉，张 勇.基于改进差分进化—生物地理学优化算法的最优潮流问题[J].电网技术，2012，36(9)：115-119.

[10]易驰韡，胡泽春，宋永华.考虑注入功率分布的随机最优潮流方法[J].电网技术，2013，37(2)：367-371.

[11]杨林峰，简金宝，韩道兰，等.基于最优中心参数的多中心校正内点最优潮流算法[J].中国电机工程学报，2012，32(4)：136-144.

[12]赵晓慧，阳育德，韦 化.求解大规模AC/DC最优潮流的连续递推内点算法[J].中国电机工程学报，2013，33(4)：171-178.