基于Hopfield NN遗传优化设计的板形缺陷识别研究

张秀玲，成 龙，郝 爽，高武杨，来永进（.燕山大学河北省工业计算机控制工程重点实验室，河北秦皇岛066004；2.燕山大学国家冷轧板带装备及工艺工程技术研究中心，河北秦皇岛066004）

基于Hopfield NN遗传优化设计的板形缺陷识别研究

张秀玲1，2，∗，成 龙1，郝 爽1，高武杨1，来永进1
（1.燕山大学河北省工业计算机控制工程重点实验室，河北秦皇岛066004；2.燕山大学国家冷轧板带装备及工艺工程技术研究中心，河北秦皇岛066004）

摘 要：针对Hopfield NN传统设计方法要求权值矩阵需要满足对称的约束，以及记忆容量和容错性低，且记忆模式易陷入伪稳定状态的缺点，本文提出了利用遗传算法（GA）优化设计Hopfield NN权值的方法，并与传统方法对比，验证了GA⁃Hopfield NN具有较大的记忆容量和较强的容错性。同时提出了GA⁃Hopfield NN的板形模式识别模型设计方案，将具有较强计算能力的反馈网络用于实时信息处理系统实现模式识别，克服了当前板形智能识别模型动态性差，容错能力低及实时性差的缺陷。同时，Hopfield NN的二值计算形式大大提高了系统的运算速度，为硬件实现和工程应用提供了新思路。

关键词：Hopfield NN；容错性；遗传算法；板形识别

0　引言

近年来随着工业产品需求层次的提高，对板带钢的尺寸精度和板形平整度有了更高的要求，因此板形控制仍是国内外研究的热点［1］。板形模式识别是板形控制系统的重要环节，识别的准确度和快速性直接影响到板形控制系统的总体性能。近年来，人工智能理论广泛应用于轧制领域，人们先后开发出基于多种神经网络和先进算法的板形模式识别模型，取得了不错的效果［2］。但是这些智能模型大多数是基于前向神经网络设计的，存在动态特性差、容错能力低、运算速度慢的缺陷，所以需要继续探索理想的板形识别方法。

联想记忆（Associative Memory，AM）是神经网络理论的一个重要组成部分，是神经网络用于智能控制、模式识别与人工智能等领域的一个重要功能。它主要利用神经网络的良好容错性，能使不完整的、污损的输入样本恢复成完整的原型，适于识别、分类等用途［3］。离散型Hopfield NN模拟了生物神经网络的记忆功能，具有动态反馈特性，相比前向网络具有更强的计算能力和容错性，将其应用于模式识别具有更大优势。离散Hopfield NN，被称为联想记忆网络，其联想记忆能力是通过权值矩阵实现的，所以选择合适的权值是发挥此网络功能的关键［4］。目前不少学者对Hopfield NN权值的设计方法进行了大量研究，如：文献［4］利用记忆模式对称原则，在Hebb规则的外积和法基础上，提出了伪外积和法，能够使多个非正交记忆样本进行正确回忆且陷入伪状态的几率变小。文献［5］提出一种改进型学习算法，利用矩阵分解的方法得到正交矩阵，再直接计算离散Hopfield NN的权值矩阵，减少了计算步骤和计算量，提高了网络的运行速度。文献［6］针对Hopfield NN自联想的特性，提出了一种新的带有粒子群优化过程的Hopfield NN分类算法，并采用了Blatt⁃Vergin学习算法，一定程度上克服了传统Hopfield NN容量低的缺点。以上设计方法，都需要所记忆样本具有一定正交性，并且所设计网络的权值应需要保证对称，使得网络结构的联想识别能力有一定局限。

本文提出了用遗传算法（GA）优化离散Hopfield NN权值的方法，对网络权值进行随机赋值，通过全局优化获得最优网络输出下的最终权值，一方面增强了非正交记忆样本的容量，另一方面打破权值对称的设计约束，并应用在板形模式识别的工程设计中，通过现场数据进行仿真，证明其具有较强的容错性和记忆能力。

1　Hopfield NN的优化设计

1.1常用设计方法

Hopfield NN是一种全连接型的神经网络，对于每一个神经元来说，输出信号通过其他神经元又反馈到输入端，所以Hopfield NN又是一种反馈型动态神经网络。其离散网络拓扑图如图1所示。

图1　Hopfield NN拓扑图Fig.1　Topology of Hopfield NN

将Hopfield NN作为联想记忆网络需要设计或训练网络的权值，使记忆和存储的模式设计或训练成网络吸引子。实现Hopfield NN联想记忆功能的运行步骤：

第一步：设定记忆模式。Hopfield NN有N个神经元，每个神经元输出为1或－1二值，则网络共有2N个状态，这2N个状态构成离散空间。在网络中存储m个n维的记忆模式（m＜n）：

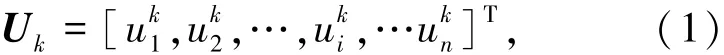
其中，k＝1，2，…，m；i＝1，2，…，n；uik∈｛－1，1｝。

第二步：设计网络权值。

a）外积法

采用外积法设计网络的权值使这m个模式是网络2N个状态空间中的m个稳定状态，即

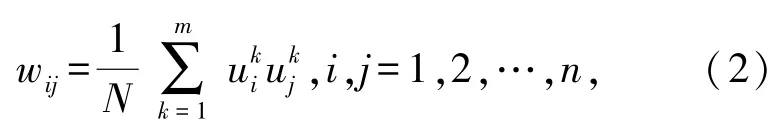
式中，1/N为调节比例的常数，这里取N＝n。考虑到离散Hopfield NN权值满足条件wij＝wji，wii＝0，则有

用矩阵形式表示，则有

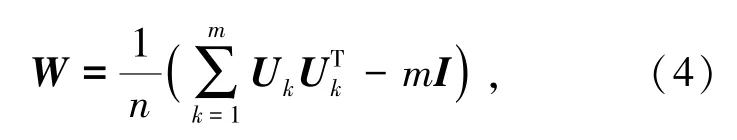
I为n×n的单位阵。

b）伪逆法

采用伪逆法设计网络权值，输入样本Uk通过权值W来映射输入输出之间的关系，有

得到

第三步：初始化网络状态。将欲识别模式U′＝［u′1，u′2，…，u′i，…u′n］T设为网络状态的初始状态，即vi（0）＝u′i，vi（0）是网络中任意神经元i在t＝0时刻的状态。

第四步：迭代收敛。根据公式

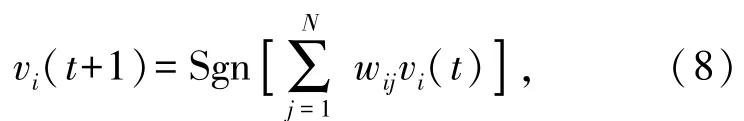
通过t＝t＋1随机地更新任一神经元的状态，反复迭代至网络中所有神经元的状态不变为止，设此时t＝T。

第五步：网络输出。此时T时刻的网络状态即为网络的输出y＝vi（T）。

外积法要求记忆样本矢量满足正交时，才能被记忆存储到网络中，限制了样本容量。伪逆学习算法能在一定程度上克服传统Hopfield NN记忆样本的约束，使网络的记忆容量有所提高。然而涉及到转置运算，新样本的学习需要老样本的累加学习，不能实现递增学习，因此运行速度较慢，并且容错性较低。本文进一步提出了GA优化Hopfield NN权值的方法，通过离线随机训练获得权值，在线模式识别，扩大了记忆样本的容量和容错性，也提高了系统的识别速度。

1.2GA对Hopfield NN权值的优化设计

GA是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法，它借鉴了进化论和遗传学说，是一种高效、并行、全局搜索的方法［7］。GA包括选择、交叉、变异3种遗传算子，在算法运行过程中，首先对可行解进行编码，形成初始种群，随后从任一初始种群出发，通过选择、交叉、变异操作，产生一群更适应环境的个体，使群体进化到搜索空间中更好的区域，如此循环最后收敛到一群最适应环境的个体，通过解码求得问题的最优解［8］。遗传算法流程图如图2所示。

本文设计的Hopfield NN板形模式识别模型，在现场轧钢板形仪采集的15个样本点基础上利用插值法，使样本点达到26个，即26个神经元，以保证网络的记忆效果，所以网络包含626个权值，即626个变量。为便于操作，GA采用实数编码。根据调试经验，GA运行过程中选择初始群体大小为20，交叉概率为0.8，变异概率自适应调整范围0.01～0.1，取实际输出与网络输出的误差均方差为适应度函数

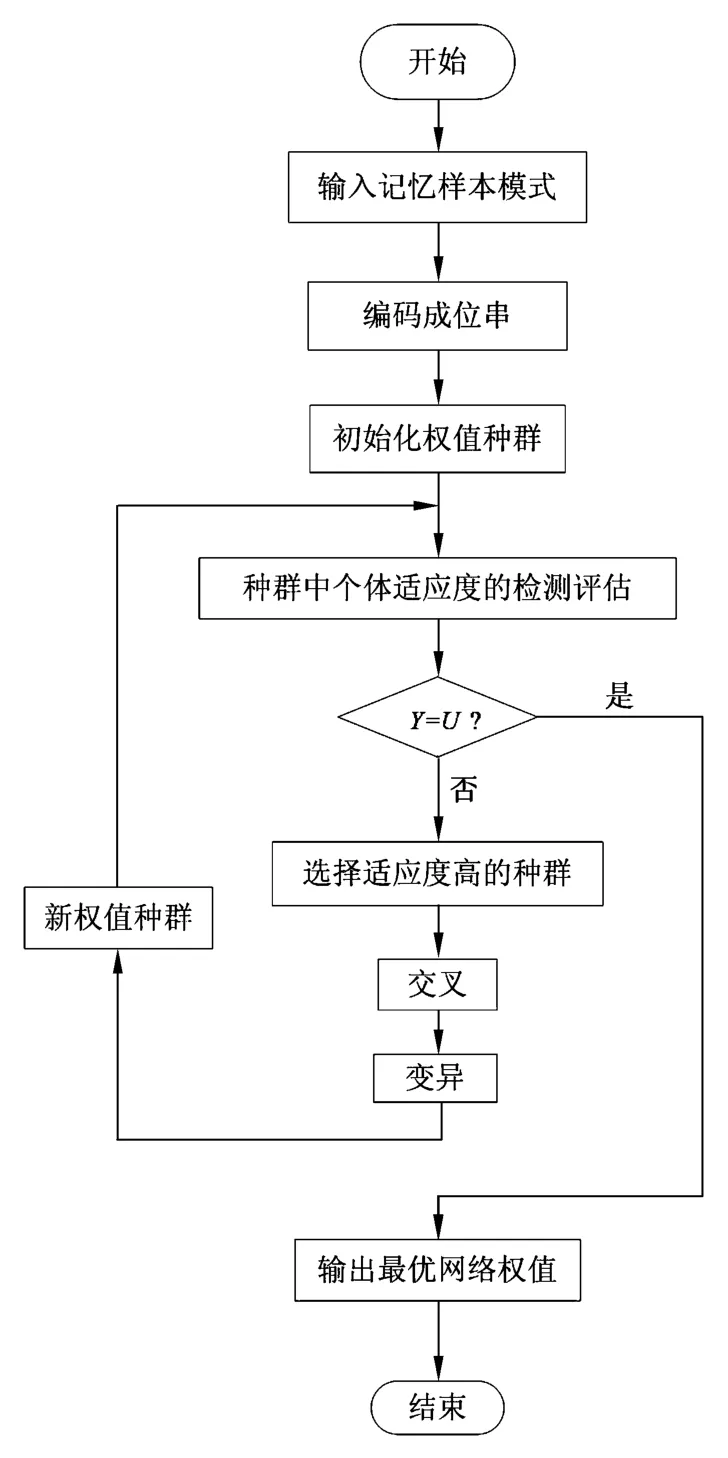
图2　遗传算法流程图Fig.2　Flow chart of genetic algorithm

2　基于GA⁃Hopfield NN的板形模式识别模型的设计

2.1板形基本模式

板形识别的目的，就是从实测的板形离散信号中判别出当前带钢中存在的板形缺陷类型属于哪一种基本模式或几种模式的组合。常见的板形缺陷基本模式包括左边浪、右边浪、中间浪、双边浪、右三分浪、左三分浪、四分浪和边中浪［9⁃10］。轧制后板形残余应力应满足沿板宽横向积分为零。残余应力沿板宽方向的分布曲线如图3所示。

基本模式的归一化方程为：

左边浪：Y1＝p1（y）＝y；

右边浪：Y2＝－p1（y）＝－y；

式中，y为带材横向板宽。

轧后板形可以表示为板形基本模式的线性组合

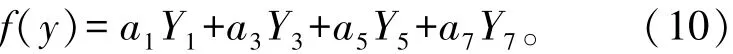
由于ai（i＝1，3，5，7）均可正可负，所以实际上表示了8种板形基本模式的线性组合［11］。a1、a3、a5、a7分别表示一次、二次、三次、四次板形偏差的隶属度，其大小表示各次板形偏差的含量。

2.2板形识别模型的建立

将利用板形仪采集到的板形应力数据所对应的各种板形缺陷模式进行编码，得到取值为1和－1的离散记忆模式。连续的板形缺陷模式对应的二值离散化处理后的缺陷模式如图4所示。

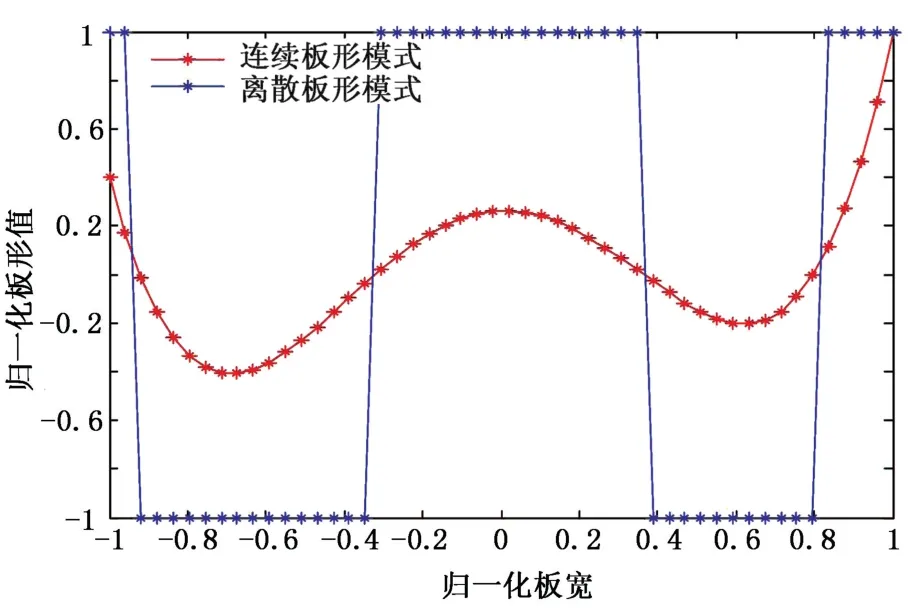
图4　连续板形对应的离散模式Fig.4　Discrete model corresponds to continuous flatness

在现场取得的板形应力值基础上利用插值法使样本点达到26个，保证样本的记忆容量，即选择26个神经元，同时为了提高所设计网络的泛化能力，选择17种板形模式进行存储，通过GA优化工具箱求适应度函数最小值［12］，使网络输出逼近实际输出。运行遗传算法，得到适应度函数变化的曲线及获得的最优个体如图5所示。

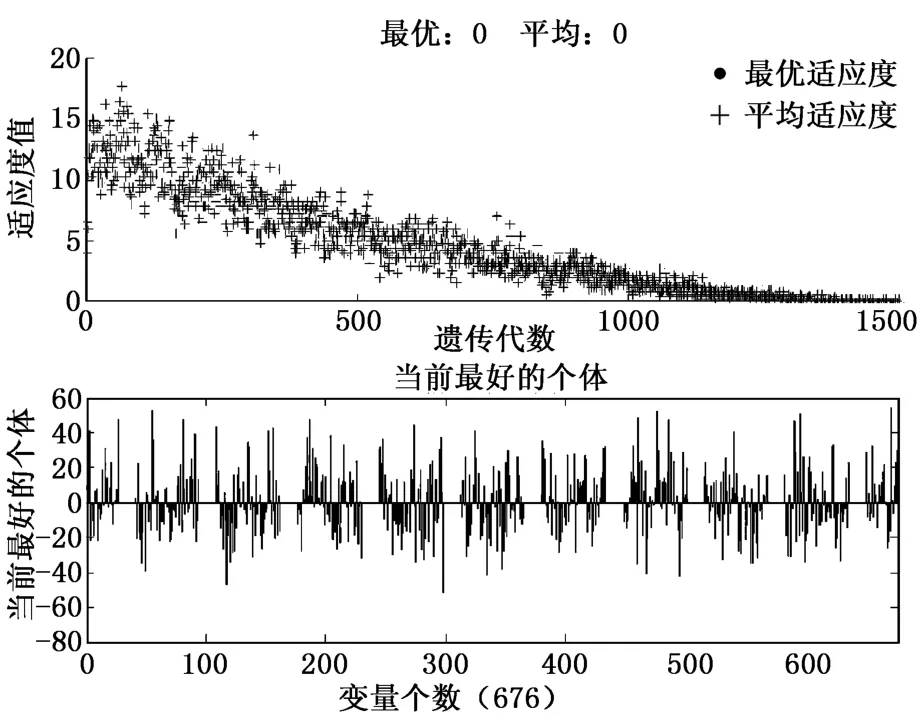
图5　遗传算法优化过程及结果Fig.5　Process and result optimized by GA

3　仿真实验结果分析

为了验证GA⁃Hopfield NN模型的板形识别能力，在MATLAB R2010a环境下，把在冷轧板带轧机现场板形仪上取得的实测板形缺陷模式数据作为网络的学习样本进行优化，本文选择了17组样本数据。网络训练结束后，在训练样本的基础上加P×rand（1）的随机干扰来检验其对板形缺陷的记忆识别能力，并与外积法、伪逆法结果进行对比，仿真结果如表1、图6和图7所示，其中MSE表示网络测试的均方差。

根据仿真实验结果分析，随着干扰强度的增加，3种方法的均方差都随着变大，识别率也逐渐降低。外积和法记忆容量有限，有一定的抗扰能力；伪逆法记忆容量提高了，抗干扰能力较差；GA法记忆容量较大，抗干扰能力较强。

GA⁃Hopfield NN表现出更强的联想记忆能力和更好的容错性，同时GA⁃Hopfield NN权值离线训练，在线识别使系统的实时处理能力更强，更易于工程实践应用。

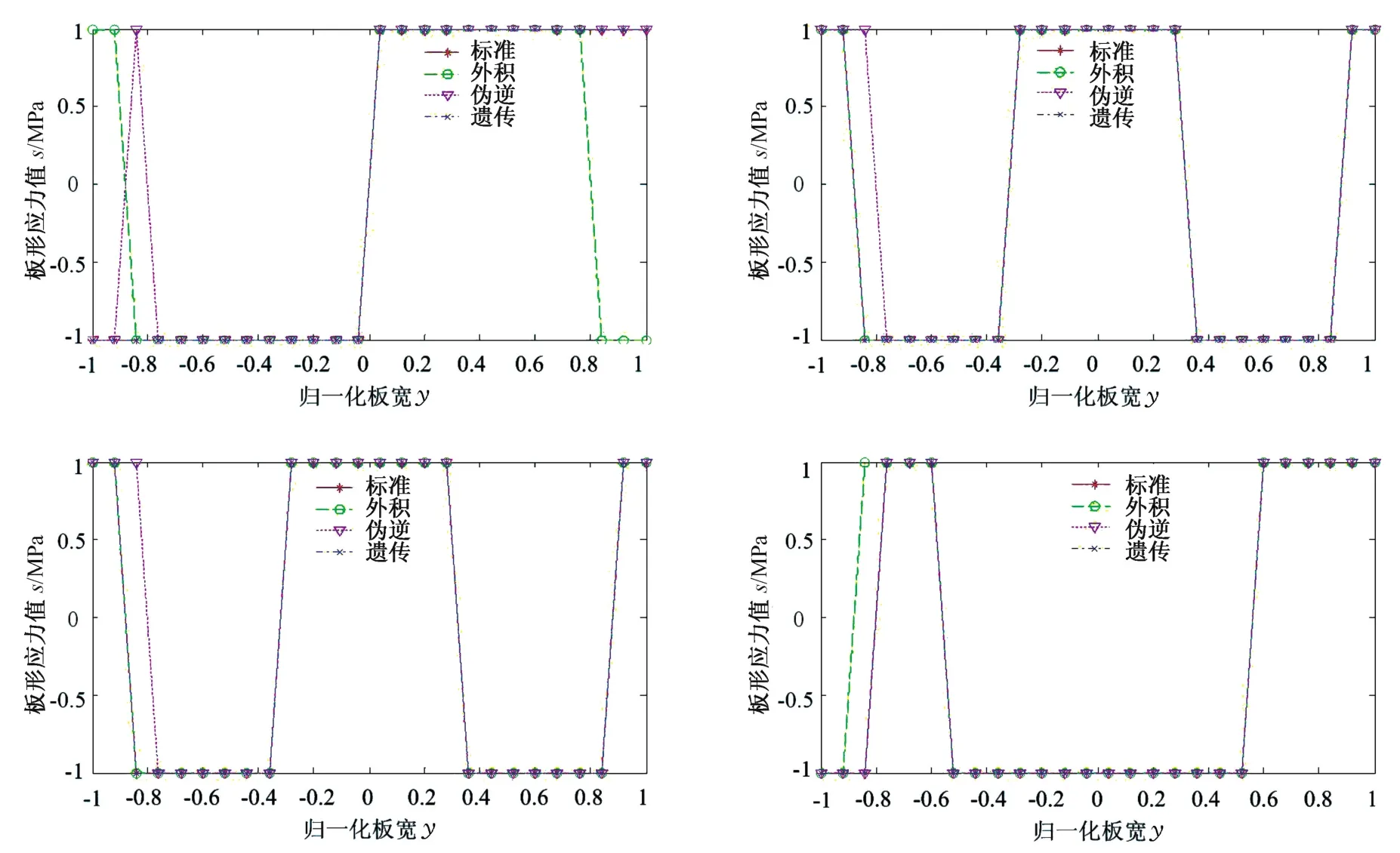
图6　P＝1.0时的板形缺陷识别结果对比Fig.6　Comparison of flatness defect recognition result at P＝1.0

图7　P＝1.5时的板形缺陷识别结果对比Fig.7　Comparison of flatness defect recognition result at P＝1.5

4　结论

1）GA⁃Hopfield NN结构模型具有反馈动力学系统的优点，计算能力比前向网络更强。并且离散二值计算对于网络的硬件（如FPGA、DSP等）实现具有更大优势，为工程的实践运用提供了理论依据。

2）GA⁃Hopfield NN一方面不要求所记忆样本具有正交性，另一方面其记忆容量较大，容错性较强，避免联想过程中陷入伪稳定点的缺陷。

3）仿真实验证明，GA⁃Hopfield NN板形模式识别新方法能够有效识别板形缺陷类型，运行速度快，识别精度高，泛化能力强，可为高精度板形自动控制策略提供依据。

参考文献

［1］Malik A S Grandhi R V.A computational method to predict strip profile in rolling mills J .Journal of Materials Processing Technol⁃ogy 2008 206 1 263⁃274.

［2］张秀玲 张少宇 赵文保 等.板形模式识别的多输出最小二乘支持向量回归机新方法 J .中国机械工程 2013 24 2 258⁃263.

［3］高隽.人工神经网络原理及仿真实例 M .北京 机械工业出版社 2013.

［4］仲伟汉 黄晞 张萧.一种设计离散型Hopfield神经网络权值的新方法 J .福建师范大学学报 自然科学版 2012 28 3 38⁃42.

［5］李荣 乔俊飞 韩红桂.一种改进型离散Hopfield学习算法 J .控制与决策 2014 29 2 241⁃245.

［6］王振华.基于Hopfield神经网络的数据分类 J .计算机应用2011 31 2 92⁃96.

［7］王晓哲 顾树生.基于遗传算法的PID神经网络解耦控制 J .控制与决策 1999 14 A11 617⁃619.

［8］谷正气 朱一凡 张沙 等.基于GA⁃BP网络的矿山路面不平度辨识 J .中国机械工程 2014 25 23 3232⁃3238.

［9］单修迎 刘宏民 贾春玉.含有三次板形的新型板形模式识别方法 J .钢铁 2010 45 8 56⁃60.

［10］ZHANG Xiu⁃ling ZHANG Shao⁃yu TAN Guang⁃zhong et al.A novel method for flatness pattern recognition via Least Squares Support Vector Regression J .Journal of Iron and Steel Research International 2012 19 3 25⁃30.

［11］PENG Yan LIU Hong⁃min.A neural network⁃based shape control system for cold rolling operations J .Journal of Materials Process⁃ing Technology 2007 202 1 54⁃60.

［12］雷英杰 张善文 李续武 等.Matlab遗传算法工具箱及应用M .西安 西安电子科技大学出版社 2005.

Research on flatness defect identification via genetic optimization design of Hopfield NN

ZHANG Xiu⁃ling1 2CHENG Long1HAO Shuang1GAO Wu⁃yang1LAI Yong⁃jin1
1.Key Laboratory of Industrial Computer Control Engineering of Hebei Province Yanshan University Qinhuangdao Hebei 066004 China 2.National Engineering Research Center for Equipment and Technology of Cold Strip Rolling Yanshan University Qinhuangdao Hebei 066004 China

AbstractA genetic algorithm GA to optimize weights of Hopfield NN called GA⁃Hopfield NN structure is proposed in the light of disadvantages of the traditional design method for Hopfield NN such as low memory capacity and error tolerant memory models easily falling into the pseudo steady state and weight matrix requested to be symmetry.GA⁃Hopfield NN has a larger memory capaci⁃y and a stronger error tolerant than that of traditional methods.A new flatness pattern recognition model based on GA⁃Hopfield NN s also set up.Feedback network that has strong computing ability is applied into real time information handling system to realize pat⁃ern recognition.Many defects that exists in current flatness intelligent recognition model such as poor dynamic low error tolerant and bad real⁃time are conquered.Meanwhile Hopfield NN adopts binary calculation form improves the operation speed of the sys⁃em greatly and provides a new way of the hardware realization and engineering application.

Key wordsHopfield NN fault⁃tolerant genetic algorithm flatness pattern recognition

作者简介：∗张秀玲（1968⁃），女，山东章丘人，博士，教授，主要研究方向为基于人工智能的复杂系统建模、控制、模式识别及计算机仿真，Email：zxlysu＠ysu.edu.cn。

基金项目：河北省自然科学基金钢铁联合研究基金资助项目（E2015203354）；河北省高校创新团队领军人才培育计划项目（LJRC013）

收稿日期：2014⁃12⁃02

文章编号：1007⁃791X（2015）03⁃0235⁃06

DOI：10.3969/j.issn.1007⁃791X.2015.03.007

文献标识码：A

中图分类号：TG335.5；TP273