基于可视性分析与能量补偿的金属矿弹性波全波形反演

孙宏宇， 韩立国,2*， 韩淼， 王志强

1 吉林大学 地球探测科学与技术学院， 长春 1300262 国土资源部应用地球物理重点实验室， 长春 1300263 中国地质调查局 油气资源调查中心， 北京 100029



基于可视性分析与能量补偿的金属矿弹性波全波形反演

孙宏宇1， 韩立国1,2*， 韩淼3， 王志强1

1 吉林大学 地球探测科学与技术学院， 长春 1300262 国土资源部应用地球物理重点实验室， 长春 1300263 中国地质调查局 油气资源调查中心， 北京 100029

采用弹性波全波形反演方法精确重建深部金属矿多参数模型，建模过程采用基于地震照明的反演策略.首先给出基于照明理论的观测系统可视性定义，利用可视性分析构建新的目标函数，对反演目标可视性较高的炮检对接收到的地震记录在波场匹配时占有更高的权重，确保了参与反演计算中的地震数据的有效性；其次将给定观测系统对地下介质的弹性波场照明强度作为优化因子，根据地震波在波阻抗界面处的能量分配特点，自适应补偿波场能量分布和优化速度梯度，以提高弹性波全波形反演过程的稳定性和反演结果的精度.理论模型和金属矿模型反演试验结果表明，基于可视性分析和能量补偿的反演策略可以使弹性波全波形反演更快地收敛到目标函数的全局极小值，获得适用于金属矿高分辨率地震偏移成像的多参数模型.

金属矿地震； 全波形反演； 弹性波； 可视性分析； 能量补偿

1 引言

近年来，国内外金属矿地震勘探技术发展较为迅速，已经成为寻找深部矿产的重要方法之一.我国在金属矿地震理论和应用方面也开展了一些探索，取得了一定进展（吕庆田等，2010，2014；廉玉广等，2011）.金属矿区人文环境与地质构造复杂、目标地质体与围岩波阻抗差较小，造成了金属矿反射地震信号能量弱和呈不连续的非层状反射，或者散射特征，往往还会受到强背景噪声的干扰，导致利用常规的速度建模技术构建的金属矿地震速度模型的精度较低，偏移成像效果差.此外，金属矿目标地质体与围岩之间波阻抗差异较小、或者存在渐变等特征，常规的纵波勘探难以取得预期效果.而基于弹性波多参数的多波多分量勘探方法有望克服传统的纵波地震勘探反射信息弱的问题（李庆春等，2007），但是常规的速度建模和成像方法的精度和分辨率对于大倾角等复杂介质都会有很大的误差（韩建光等，2013），为此需要发展高精度地震波速度和密度等多参数模型重建和偏移成像的方法.

地震全波形反演（FWI）理论于20世纪80年代建立（Tarantola,1984; Mora,1987）并逐步得到完善和改进，近年来更是取得了迅速发展（Virieux and Operto，2009；韩淼，2014）.同时，弹性波全波形反演（EFWI）的计算速度和精度也有了很大的提高（Castellanos et al.,2011; Wang et al., 2012; Xiong et al., 2013; Son et al., 2014）.继Pratt等（1998）将声波近似的全波形反演方法引入到频率域后，Brossier等（2009）在频率域实现了弹性波FWI，并采用多尺度策略提高反演精度.而时间域的多尺度反演方法能灵活选取时窗分离波场，便于降低反演问题的非线性性（Boonyasiriwat et al.,2009; Fichtner et al.,2013），更适用于处理波场复杂的实际资料.由于波场中各属性参数相互耦合，因此利用弹性波全波形反演方法重建地下介质波场参数分布更加困难.Köhn等（2012）详细讨论了时域EFWI选用不同的参数组合，如拉梅系数，地震波速度或波阻抗作为反演参数时，参数间的相互影响.Xu和McMechan（2014）综合考虑各个参数的梯度变化，在得到多参数相互独立的搜索方向和步长后，沿着多参数合成的搜索方向寻找一个最优步长，以较快的收敛速度实现任意参数组合的反演；Groos等（2014）引入黏弹性介质的品质因子同时反演浅部体波和瑞雷波；Ren和Liu （2015）提出联合变差分阶数正演和基于子波的多尺度反演策略.这些方法的提出使得弹性波全波形反演更加成熟，已经成功应用到了海洋（Prieux et al., 2013；Raknes et al., 2015）和陆地地震勘探实际数据的多参数建模中（Plessix and Pérez, 2015；Borisov and Singh, 2015）.

地震照明技术通过建立地质模型人工模拟野外采集方式，分析地震波在介质中传播过程中能量的分布，评价观测系统参数（谢小碧等，2013），提高AVO/AVA分析精度（Askim et al., 2010）和优化偏移成像剖面（Zhou et al.,2014）.Yang等（2013）将照明能量作为加权因子引入到成像域声波全波形反演中，消除建立速度模型过程中照明不均的影响.Bian等（2015）利用照明技术估计全波形反演中观测系统参数对反演结果的作用.陈永芮等（2013）利用双向照明优化观测系统并对声波全波形反演梯度进行能量补偿.应用全波形反演处理实际数据时，可以根据先验模型进行可视性分析找到最优炮点分布和最佳接收范围，并在对应位置加密震源和检波器，使观测数据包含更多的有效信息，提高反演精度和稳定性.由于时间域全波形反演的计算复杂度与模型大小及观测系统有直接关系，随着震源点数的增加，计算量成正比增长.Wang和Rao（2009）在声波全波形反演中采用层剥离的反演方法，解决了有限偏移距的波场效应和反演误差传递等问题，逐层反演以重构深部纵波速度模型，但这种方法的计算量较大，正比于对底层的人为分层数目.本文提出一种基于可视性分析与自适应能量补偿的弹性波全波形反演方法，并应用于复杂的金属矿地震勘探多参数建模处理.首先将观测系统中单个震源和检波器对目标体的总照明强度定义为该炮检对对目标体的可视性，对弹性波全波形反演中的观测系统进行可视性分析并计算出可视性分析平面图，将可视性作为加权因子引入到全波形反演中目标函数的计算，给出基于可视性的目标函数，以增加观测波场和模拟波场相互匹配过程中与目的层相关性较高的炮检对的残差权重.其次，对于金属矿复杂地区存在的照明阴影区而导致弹性波场能量不均匀分布、成像效果差的问题，根据给定的观测系统计算波场对地下介质的双向照明强度，构建自适应的加权梯度函数，使得地震波场能量近似均衡分布，从而改善全波形反演效果.

2 方法原理

2.1 弹性波波形反演

全波形反演中的目标函数E可以表示为

-uobs（xs,xr,t）]2dt,

（1）目标函数E对模型参数m求导可得到梯度方向为

（2）

其中，ucal和uobs分别是模拟波场和观测波场，δd是两者间的残差.若雅克比矩阵∂u/∂m已知，则对模型空间中所有扰动进行积分可计算数据空间波场的总变化值. 同理，对数据空间的波场扰动求积分可以得到模型空间的变化量为（Tarantola,2005）

（3）

（4）

其中，*代表相应的共轭矩阵.由于这种反问题的解并非唯一，即δu≠δu′，δm≠δm′，但由于[∂u（m）/∂m]*=∂u（m）/∂m，因此若将数据空间的扰动看作残差，则从数据空间到模型空间的映射就等同于目标函数的梯度：

（5）

因此，根据一阶扰动形式下的弹性波方程和格林函数，可以得到纵波速度vp、横波速度vs和密度ρ的梯度表达式为（Mora,1987）

（6）

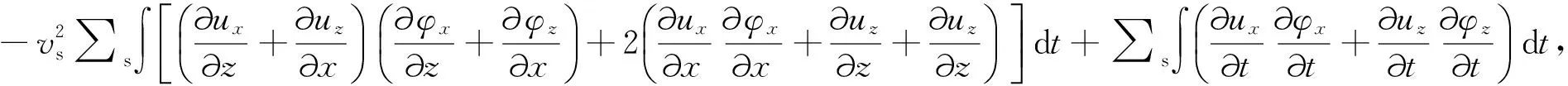
（8）

其中，ux和uz分别是在震源点激发的弹性波场的水平分量和垂直分量，φx和φz分别是在检波点位置激发的反传残差波场的水平分量和垂直分量.选用合适的优化方法，沿着目标函数的负梯度方向，利用迭代公式（9）对初始模型m0迭代更新，即可得到目标函数的全局最优解，公式（9）为

mn+1=mn-αnPδmn，

（9）

其中，αn为第n次迭代的步长，P为预处理算子.若选用牛顿法优化参数模型，则P为海森矩阵的逆，若选用高斯牛顿法优化参数模型，则P为对角海森矩阵的逆.2.2 基于可视性的目标函数

金属矿地震勘探由于地表条件的复杂和地下介质的不均匀分布等因素的干扰，只有部分位置的炮点和检波点能激发并接收到与探测地质体有关的地震波信息，通过波动方程照明分析，可以得到观测系统中单个震源和检波点对目的层的归一化总照明强度即观测系统的可视性，它能直观地描述观测系统中任意炮捡对的观测数据对于成像或反演的有效作用程度.计算基于可视性的目标函数来优化全波形反演中对应炮检对的模拟地震记录与观测记录之间的残差，提高了与目的层有关的地震记录在目标函数中的权重，重点反演深部目标体的构造参数信息.对于二维观测系统中的任意炮检对（xs,xr），其对地下介质的照明强度为

（10）

（11）

（12）

（13）其中，vis表示地震波由xs处的震源激发xr处接收时成像目标范围内整体的照明强度，即炮检对（xs,xr）的可视性.

为便于估计任意一炮检对所得到的地震记录在波形反演计算时波场匹配过程中的作用，我们用可视性的平均值作为判别标准，大于平均值说明该炮检对接收到的地震记录与目的层的相关性较高，因此经预处理后可以得到该观测系统对目的层的相对可视性vis′为

vis′（xs,xr）=φ×vis（xs,xr），

（14）

（15）

其中，ns和nr分别为炮点和检波点的个数.φ为vis的平均值的倒数.当相对可视性的值大于1时，即该炮检对的可视性大于观测系统对目的层的可视性平均值，将其引入到波形反演中目标函数的计算，可以得到基于可视性的弹性波全波形反演的目标函数为

[ucal（xs,xr,m,t）-uobs（xs,xr,t）]2dt,

（16）

此时，与目标体相关性较高的地震数据在波场匹配时将会占有更多的权重.

图1a和c分别为观测系统中某炮在MarmousiII模型及反演初始模型上正演的水平分量地震记录，图1b和d为相应的垂直分量地震记录.该炮对应的所有检波点对目标体的相对可视性曲线如图2所示，该观测系统中共有400个检波器.可以看出，位于第120到190号和第280到400号之间的检波器与目标体的相关性较高，可以接收到更多来自于反演目标体的波场信息.以此可视性作用于弹性波全波形反演中波场水平分量和垂直分量的残差（图3a和c，对应的位置残差能量增强（图3b和d）可以使弹性波全波形反演计算时充分利用更多的有效数据，提高反演精度和稳定性.

图1 MarmousiII模型上正演的弹性波场（a）x分量、（b）z分量和初始模型上正演的弹性波场（c）x分量、（d）z分量

图2 观测系统中某炮及其对应所有检波点的相对可视性曲线

图3 x分量观测与模拟记录的（a）原始残差和（b）经能量加权后的残差以及z分量观测与模拟记录的（c）原始残差和（d）经能量加权后的残差

2.3 自适应能量补偿

正是因为环保的自觉遵守，以及理念超前，所以无锡工厂自2012年起连年被无锡新区评为绿标企业。爱克发用行动证明了印刷业完全可以成为绿色环保产业。

反射能量较强的地震记录在波形反演数据拟合时占有更大的比重，而能量较弱的波场对应的速度结构在反演过程中得不到较好的恢复，即使其速度结构与真实模型相差很大，因此，这种波场能量的不均匀分布会影响反演结果的稳定性.两种原因会导致地震波能量在地下介质中不均匀分布，一是由于地震波的几何扩散现象，波场能量随着传播深度的增加而减小；二是由于地下介质的复杂性，使得波在其传播方向上存在照明阴影区.利用波动方程理论得到的双向照明强度自适应加权梯度，可以同时补偿因观测系统中偏移距不足导致深部波场能量弱的问题和复杂介质中存在照明盲区而引起的能量损失，加权因子取决于在地震波的传播方向对应位置处的照明强度，这在数学上类似于利用海森矩阵优化梯度，得到牛顿类优化方法中的模型更新量.地震波在弹性介质分界面处的能量分配情况可以用Zoeppritz方程描述.波场由高速介质向低速介质传播时，透射系数T>1，地震波的透射能量强于反射能量，界面下部的照明强度高于界面上部，此时可以用双向照明强度反比例加权于相应参数的梯度；相反，地震波场由低速向高速介质中传播时，透射系数T<1，则地震波的反射能量强于透射能量，界面上部的照明强度高于界面下部，此时可以用归一化后的照明强度正比例加权于相应参数的梯度.由此可得到弹性波反演中经自适应能量补偿后的模型更新量δm′为

（17）

其中，I是弹性波场照明强度.

3 模型试验与效果分析

3.1 MarmousiII模型

采用MarmousiII模型（图4）来测试本文的反演方法.模型网格大小为174×500，网格间距为20 m，横向长10 km，纵向深3.48 km.观测系统模拟水中激发纵波，以海底多波观测方式采集接收纵波和转换波，100个震源水平分布于海水面以下40 m处，400个三分量的检波器位于海底.为了分析观测系统的可视性，设目的层为位于深部断层下的含油藏的圈闭构造，如图4中黑框所示.采样率为2 ms，地震记录长度为6s.震源为主频10 Hz的雷克子波.反演选用LBFGS优化方法，最大迭代次数为100次.

对于给定的目标范围，经照明统计可以得到该观测系统对地下介质的相对可视性如图5a所示，图中横纵坐标分别代表该观测系统中检波器和震源的序号，各点的数值代表当地震波由纵坐标对应位置

处的震源激发，横坐标对应位置处的检波器接收时，该炮检对记录对目的层的相对可视性.可以看出该观测系统中，第40到第80个震源，第100到第230个检波器，以及第280到第400个检波器所对应的相对可视性均大于1，说明这个范围内的炮检对接收到的波场对目的层的成像起到主要作用.图5b为该观测系统对地下介质的弹性波场照明强度，由于观测系统中震源和检波器主要分布在模型中部，因此模型两侧的照明较弱，中上部照明较强.此外由于地震波的几何扩散现象以及复杂介质引起的照明不均，模型深部以及复杂断裂带下方的照明能量较弱.我们应用可视性分析方法提高对目的层成像作用较大的炮检点对应的水平分量和垂直分量的残差在波场匹配中的权重，同时采用自适应算法进行能量补偿.

图6为两种反演方法均迭代100次后的反演结果.纵波速度、横波速度和密度三种参数均得到了较好的恢复，可以看出，基于可视性分析和能量补偿的EFWI的反演结果要明显优于常规EFWI.从反演结果、真实模型和初始模型中提取模型中水平距离为5.2 km处的参数变化曲线，如图7所示.相比于常规EFWI，本文提出的EFWI方法反演的纵波速度、横波速度和密度曲线更加趋近于真实模型，对复杂构造的有效重构同时加快了反演的收敛速度，使本文方法在相同的迭代次数条件下获得更加精确的反演结果.3.2 金属矿模型弹性波全波形反演对安徽省庐枞盆地某矿床的复杂地球物理模型（图8）采用弹性波全波形反演方法重建速度和密度多参数模型.该模型总体呈复杂的似层状、平缓透镜状，空间上表现为穹隆状，中心以侵染状磁铁矿为主，富、厚矿多环于四周.矿床由多个矿体组成，其中规模较大的只有3个矿体，其余均为小矿体（吕庆田等，2010；廉玉广等，2011）.对该模型进行重采样后得到的纵波速度模型如图9a所示.模型网格点数为120×400，网格间距为20 m，模型横向长8 km，纵向深2.4 km.主矿体埋深距地表1.3～1.8 km间，且厚度变化较大.横波速度和密度可以在纵波速度基础上由经验公式得出（Brocher, 2005; Xu and McMechan,2014），如图9b和c所示，公式为

图4 MarmousiII模型

图5 （a）观测系统对指定目的层的可视性和（b）弹性波场照明强度

图6 反演结果

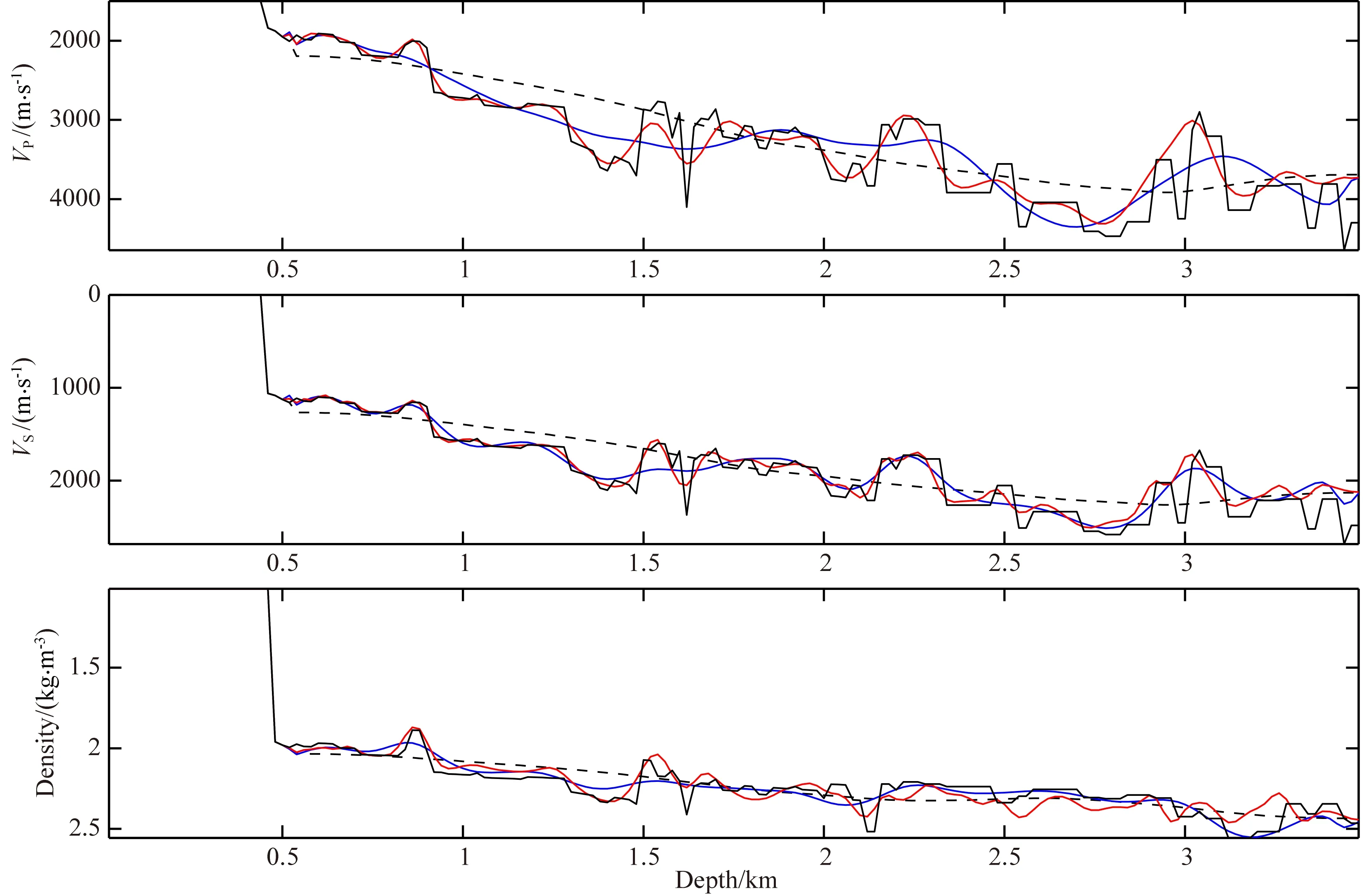
图7 不同方法反演的参数剖面对比（x=5.2 km处）：真实模型（黑实线）、初始模型（黑虚线）、常规EFWI反演结果（蓝线）、基于可视性分析和能量补偿的EFWI反演结果（红线）

图8 S1线过罗河矿体地球物理模型（据廉玉广等，2011）

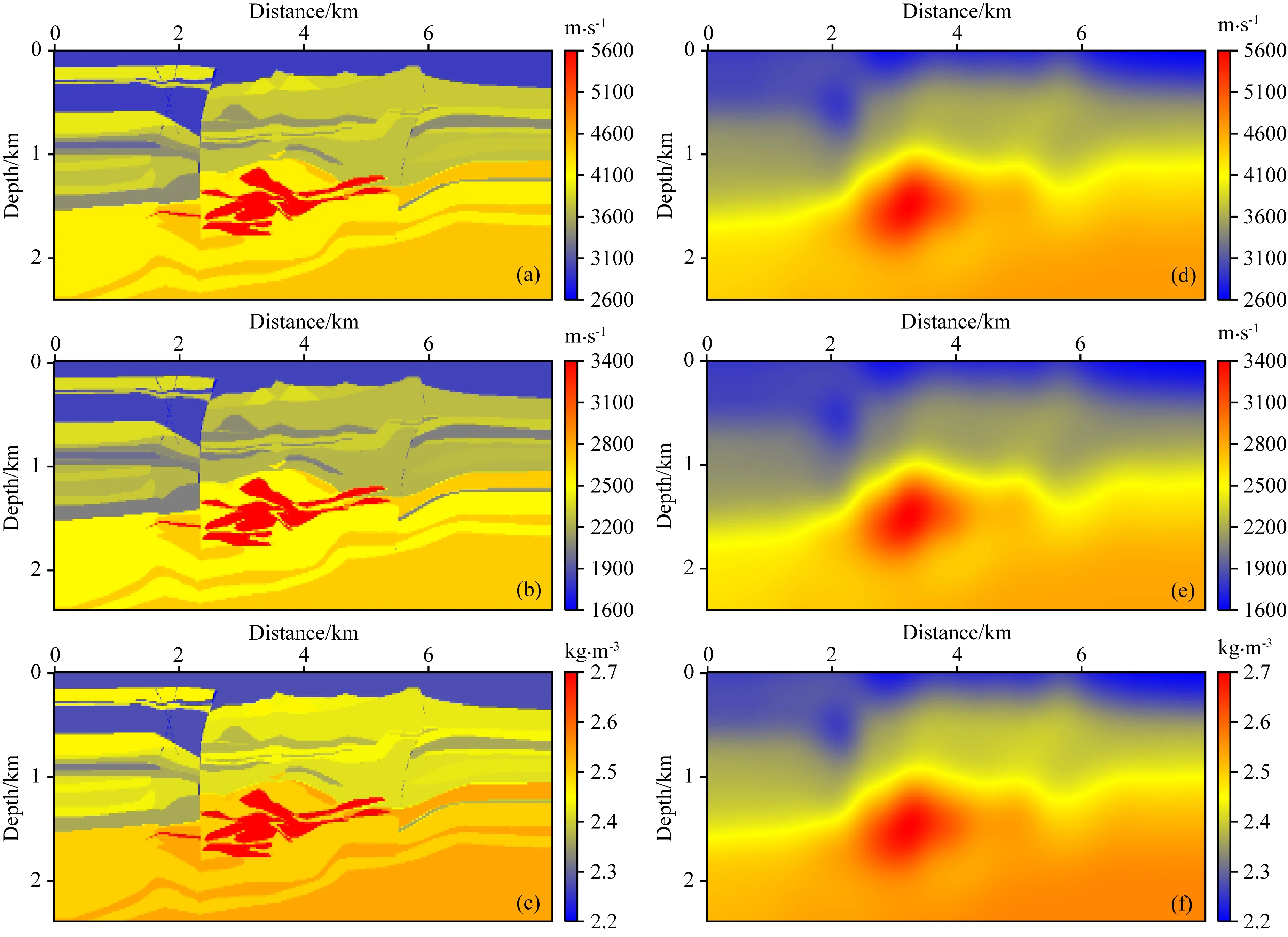
图9 金属矿多参数模型

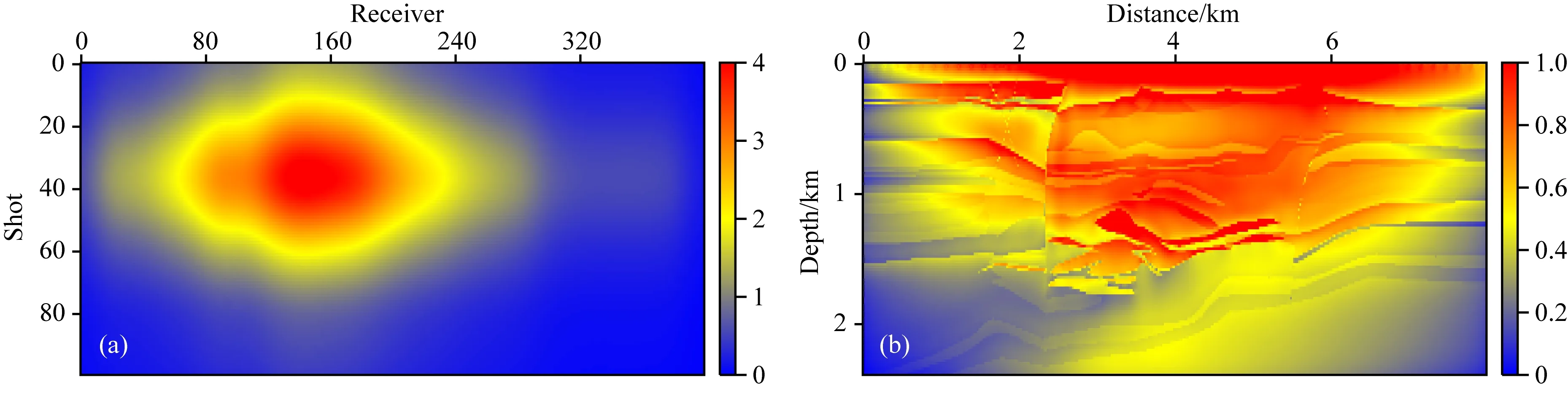
图10 （a）观测系统对指定矿体的可视性和（b）弹性波场照明强度

图11 金属矿多参数模型反演结果

（18）

（19）

应用于弹性波全波形反演的初始模型如图9d、e和f所示.采样率为2ms，地震记录长度为2s.震源子波为主频10Hz的雷克子波.反演选用LBFGS优化方法，最大迭代次数为100次.观测系统中100个震源水平分布于地表下40m处，起始震源位于水平距离40m处，震源间距为80m.400个检波器深度均为20m，起始坐标和间距分别为0m和20m.

选定的目标范围即为矿体所在的位置，对该观测系统进行可视性分析的结果如图10a所示，弹性波场照明强度如图10b所示，弹性波的能量除了在地表较强，在矿体部位也有所聚集.将照明分析的结果引入到全波形反演中，得到基于地震照明的弹性波全波形反演结果如图11d、e和f所示.与常规弹性波全波形反演的结果（图11a、b和c）对比可以看出，矿体轮廓的反演更加清晰，说明在反演过程中引入可视性分析和照明补偿，可以有效地改善反演效果.

4 结论

（1）基于可视性分析的弹性波全波形反演策略可以适用于金属矿等复杂介质构造的多参数建模.通过照明统计分析可以得到给定观测系统对反演目的层的可视性，将其应用于波场匹配过程中对应炮检点的残差能量计算.构建基于可视性的反演目标函数，可以充分利用来自于目的层的有效地震信息，提高反演精度.

（2）由于观测系统对地下介质的照明强度可以直观地描述地震波能量的分布情况，利用Zoeppritz方程将弹性波场照明强度引入到全波形反演中，使得地震波场的能量自适应地均衡分布和优化梯度，改善反演质量.

（3）弹性波全波形反演方法可以高精度地重构深部金属矿地质体的多参数模型，包括纵横波速度和密度，可以实现金属矿区地下介质构造的高精度偏移成像.由于弹性波全波形反演可以利用多波多分量全波场信息，克服了单一的纵波地震勘探时由于弱阻抗差可能带来的不利影响，为有效地应用地震勘探技术开展深部矿产资源探测提供了新途径.

致谢 感谢国家自然科学基金（41374115）和国家科技重大专项（2011ZX0502500104）的支持，感谢评审专家的宝贵意见，在论文研究过程得到了王者江教授、巩向博副教授、张凤蛟博士的有益帮助，在此一并致谢.

Askim O J, Albertin U, Matson K, et al. 2010. Wave-equation-based illumination determination for Amplitude versus Angle risk assessment. ∥80th SEG Annual Meeting Expanded Abstracts. Expanded Abstracts, 3263-3267.

Bian A F, Zou Z H, Zhou H W, et al. 2015. Evaluation of multi-scale full waveform inversion with marine vertical cable data.JournalofEarthScience, 26（4）: 481-486.

Boonyasiriwat C, Valasek P, Routh P, et al. 2009. An efficient multiscale method for time-domain waveform tomography.Geophysics, 74（6）: WCC59-WCC68. Borisov D, Singh S C. 2015. Three-dimensional elastic full waveform inversion in a marine environment using multicomponent ocean-bottom cables: a synthetic study.GeophysicalJournalInternational, 201（3）: 1215-1234.

Brocher T M. 2005. Empirical relations between elastic wavespeeds and density in the earth′s crust.BulletinoftheSeismologicalSocietyofAmerica, 95（6）: 2081-2092.

Brossier R, Operto S, Virieux J. 2009. Seismic imaging of complex onshore structures by 2D elastic frequency-domain full-waveform inversion.Geophysics, 74（6）: WCC105-WCC118.

Castellanos C, Etienne V, Hu G H, et al. 2011. Algorithmic and methodological developments towards full waveform inversion in 3D elastic media. ∥81st SEG Annual Meeting Expanded Abstracts. Expanded Abstracts, 2793-2798.

Chen Y R, Li Z C, Qin N, et al. 2013. Full waveform inversion with wave equation bi-directional illumination optimization.ProgressinGeophysics（in Chinese）, 28（6）: 3015-3021, doi: 10.6038/pg20130624.

Fichtner A, Trampert J, Cupillard P, et al. 2013. Multiscale full waveform inversion.GeophysicalJournalInternational, 194（1）: 534-556.

Groos L, Schäfer M, Forbriger T, et al. 2014. The role of attenuation in 2D full-waveform inversion of shallow-seismic body and Rayleigh waves.Geophysics, 79（6）: R247-R261.

Han J G, Wang Y, Lu J, et al. 2013. Elastic wave Kirchhoff pre-stack depth migration velocity analysis.OilGeophysicalProspecting（in Chinese）, 48（5）: 694-699.

Han M. 2014. Methods and application of full waveform inversion for abyssal seismic data [Phd′s thesis]. （in Chinese）. Changchun: Jilin University.

Köhn D, De Nil D, Kurzmann A, et al. 2012. On the influence of model parametrization in elastic full waveform tomography.GeophysicalJournalInternational, 191（1）: 325-345.

Li Q C, Liu G H, Li Q. 2007. Multi-component seismic explorations-directions of seismic exploration for metal deposits. （in Chinese）. Xian: Shanxi Scientific and Technique Press.

Lian Y G, Lu Q T, Han L G, et al. 2011. Research of seismic modeling of complex metal ore body.ActaGeologicaSinica（in Chinese）, 85（5）:887-898.

LÜ Q T, DONG S W, SHI D N, et al. 2014. Lithosphere architecture and geodynamic model of middle and lower reaches of Yangtze metallogenic belt: A review from SinoProbe.ActaGeologicaSinica（in Chinese）, 30（4）: 889-906.

LÜ Q T, HAN L G, Yan J Y et al. 2010. Seismic imaging of volcanic hydrothermal iron-sulfur deposits and its hosting structure in Luzong ore district.ActaGeologicaSinica（in Chinese）, 26（9）: 2598-2612.

Mora P. 1987. Nonlinear two-dimensional elastic inversion of multioffset seismic data.Geophysics, 52（9）: 1211-1228.

Plessix R É, Pérez Solano C A. 2015. Modified surface boundary conditions for elastic waveform inversion of low-frequency wide-angle active land seismic data.GeophysicalJournalInternational, 201（3）: 1324-1334.

Pratt R G, Shin C, Hicks G J. 1998. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion.Geophysics, 133（2）: 341-362.

Prieux V, Brossier R, Operto S, et al. 2013. Multiparameter full waveform inversion of multicomponent ocean-bottom-cable data from the Valhall field. Part 2: imaging compressive-wave and shear-wave velocities.GeophysicalJournalInternational, 194（3）: 1665-1681.

Raknes E B, Arntsen B, Weibull W. 2015. Three-dimensional elastic full waveform inversion using seismic data from the Sleipner area.GeophysicalJournalInternational, 202（3）:

1877-1894.

Ren Z M, Liu Y. 2015. Elastic full-waveform inversion using the second-generation wavelet and an adaptive-operator-length scheme.Geophysics, 80（4）: R155-R173.

Son W, Pyun S, Shin C, et al. 2014. Laplace-domain wave equation modeling and full waveform inversion in 3D isotropic elastic media.JournalofAppliedGeophysics, 105: 120-132.

Tarantola A. 1984. Inversion of seismic reflection data in the acoustic approximation.Geophysics, 49（8）: 1259-1266.

Tarantola A. 2005. Inverse problem theory and methods for model parameter estimation. Paris, France: SIAM, 128-133.

Virieux J, Operto S. 2009. An overview of full-waveform inversion in exploration geophysics.Geophysics, 74（6）: WCC127-WCC152.

Wang J, Zhou H, Tian Y K, et al. 2012. A new scheme for elastic full waveform inversion based on velocity-stress wave equations in time domain. ∥82nd SEG Annual Meeting Expanded Abstracts. Expanded Abstracts, 1-5.

Wang Y H, Rao Y. 2009. Reflection seismic waveform tomography.JournalofGeophysicalResearch:SolidEarth, 114（B3）: B03304.

Xiong J L, Lin Y, Abubakar A, et al. 2013. 2.5-D forward and inverse modelling of full-waveform elastic seismic survey.GeophysicalJournalInternational, 193（2）: 938-948.

Xu K, McMechan G A. 2014. 2D frequency-domain elastic full-waveform inversion using time-domain modeling and a multistep-length gradient approach.Geophysics, 79（2）: R41-R53.

Yang T N, Shragge J, Sava P. 2013. Illumination compensation for image-domain wavefield tomography.Geophysics, 78（5）: U65-U76.

Zhou H M, Chen S C, Ren H R, et al. 2014. One-way wave equation least-squares migration based on illumination compensation.ChineseJ.Geophys., 57（5）: 726-738.

Xie X B, He Y Q, Li P M. 2013. Seismic illumination analysis and its applications in seismic survey design.ChineseJ.Geophys. （in Chinese）, 56（5）: 1568-1581, doi: 10.6038/cjg20130515.

附中文参考文献

陈永芮, 李振春, 秦宁等. 2013. 波动方程双向照明优化的全波形反演. 地球物理学进展, 28（6）: 3015-3021, doi: 10.6038/pg20130624.韩建光, 王赟, 芦俊等. 2013. 弹性波Kirchhoff叠前深度偏移速度分析. 石油地球物理勘探, 48（5）: 694-699.

韩淼. 2014. 深水区地震全波形反演策略与应用[博士论文]. 长春: 吉林大学.

李庆春, 刘国华, 李勤. 2007. 多波多分量地震-金属矿地震勘探的方向. 西安: 陕西科学技术出版社.

廉玉广, 吕庆田, 韩立国等. 2011. 复杂金属矿体地震波正演模拟研究——以庐枞盆地罗河、泥河和大包庄矿床为例. 地质学报, 85（5）: 887-899.

吕庆田, 董树文, 史大年, 等. 2014. 长江中下游成矿带岩石圈结构与成矿动力学模型——深部探测（SinoProbe）综述. 岩石学报, 30（4）: 889-9064.

吕庆田, 韩立国, 严加永等. 2010. 庐枞矿集区火山气液型铁、硫矿床及控矿构造的反射地震成像. 岩石学报, 26（9）: 2598-2612.

谢小碧, 何永清, 李培明. 2013. 地震照明分析及其在地震采集设计中的应用. 地球物理学报, 56（5）: 1568-1581, doi: 10.6038/cjg20130515.

（本文编辑 张正锋）

Elastic full waveform inversion based on visibility analysis and energy compensation for metallic deposit exploration

SUN Hong-Yu1，HAN Li-Guo1,2*，HAN Miao3，WANG Zhi-Qiang1

1CollegeofGeo-explorationScienceandTechnology,JilinUniversity,Changchun130026,China2KeyLaboratoryofAppliedGeophysics,TheMinistryofLandandResources，Changchun130026,China3OilandGasSurveyofChinaGeologicalSurvey,Beijing100029,China

The weak and discontinuous reflections and scattering features in complex environments make it difficult to construct velocity models suitable for imaging in conventional P- wave seismic exploration for metallic deposits. Multi-wave and multi-component seismic exploration technology may have the advantages in effort to solve this problem. Elastic full waveform inversion （EFWI） exploiting the multi-component and pre-stack seismic data can reconstruct highly accurate multi-parameter models for imaging complex deposit structure in the deep subsurface. The EFWI method based on visibility analysis and adaptive energy compensation is introduced in this paper which can utilize prior information more adequately relevant to vector seismic fields from the target.For a specific geometry in seismic acquisition, only signals from sources and receivers within a certain extent have effect on the inversion and imaging about the objective body. According to the contribution for a single shot-geophone pair to the imaging of the objective body, the statistical analysis method is used to obtain the whole illumination intensity of the target zone which is defined as the visibility of the single source-receiver pair. To improve the inversion result by utilizing the seismic information related to the target zone as much as possible without increasing computation and acquisition costs, we can construct the objective function of EFWI based on geometry visibility to increase the proportion of residuals related to the target zone during wavefield matching. FWI is a data-fitting procedure between observed and calculated data. Wavefields with weaker energy make less contribution to the misfit of objective function even though the velocity contrast is bigger. The uneven distribution of energy due to several cases can be expressed by seismic illumination. So bi-directional illumination intensity of the elastic wavefield is used as a weighting factor to adaptively optimize and balance the gradients of EFWI. Zoeppritz equations control the process of automatic compensation because they describe the energy distribution of seismic waves across the interface of impedance.The EFWI algorithm proposed in this paper is implemented by the finite-difference method to calculate the elastic wavefields in the time domain and LBFGS optimization method to update the initial models. The multi-parameter gradients （density, P-wave and S-wave velocity） are calculated by the cross-correlation between forward and backward wavefields in the time domain. First, the validity of our inversion method is verified on the MarmousiII model. The accuracy of inversion results with visibility analysis and energy compensation is improved compared with conventional EFWI. The model test results based on one metallic model of Luzong Basin also illustrate that our new method makes the inversion converge to global minimum of objective function faster and provides accurate and multi-parameter models which can be applied to high-resolution seismic migration imaging of metallic deposits.The numerical results show that the elastic full waveform inversion algorithm based on visibility analysis utilizes the effective information from the target zone adequately. Introducing the illumination intensity of the elastic wavefield to EFWI by transmission coefficients between two layers can also balance the energy distribution of wavefields adaptively. Both of the two inversion strategies with illumination can improve the accuracy of imaging. The EFWI method can accurately reconstruct deep and multi-parameter models for metallic deposits, including density, P and S wave velocity, which makes it possible to obtain high-resolution migration imaging about deposit structures.

Metallic deposits； Full waveform inversion； Elastic wave； Visibility analysis； Energy compensation

国家高技术研究发展计划（863计划）重大项目课题（2014AA06A605）和国家深部探测专项第3项目（SinoProbe-03）联合资助.

孙宏宇，女，1992年生，硕士研究生，主要从事地震波场正反演研究. E-mail: sunhongyu2014@foxmail.com

*通讯作者 韩立国，男，1961年生，教授，博士生导师，主要从事地震数据处理解释工作. E-mail: hanliguo@jlu.edu.cn

10.6038/cjg20151222.

10.6038/cjg20151222

P631

2015-11-03，2015-11-26收修定稿

孙宏宇， 韩立国， 韩淼等. 2015. 基于可视性分析与能量补偿的金属矿弹性波全波形反演.地球物理学报，58（12）:4605-4616,

Sun H Y, Han L G, Han M, et al. 2015. Elastic full waveform inversion based on visibility analysis and energy compensation for metallic deposit exploration.ChineseJ.Geophys. （in Chinese）,58（12）:4605-4616,doi:10.6038/cjg20151222.