新课标背景下的数量关系分析教学

卞庆龙

课改前小学数学应用题教学十分重视数量关系的分析，但第一轮课改后，数量关系教学有被弱化和边缘化的倾向。不少教师在教学中引导学生过多地关注信息的收集、整理，对数量关系的分析往往一带而过，使学生感到无从下手，不知道怎样去思考，学生解决实际问题常常是在生活经验或者直觉的支持下完成的。虽然他们把问题解决了，但对解决问题的过程与方法缺少有意识的体验，不利于学生形成解题策略、提炼解题经验。《课标》修订时，明确指出：“了解分析和解决问题的一些基本方法”，“在具体情境中，了解常见的数量关系：总价=单价×数量、路程=速度×时间，并能解决简单的实际问题。”因此，在解决问题教学中，我们必须高度重视数量关系的教学。

下面笔者粗浅地谈一谈新课标背景下的数量关系教学，与诸君商榷。

一、 结合运算意义，建立基本模型

重视数量关系分析是传统应用题教学的重要经验，但是传统应用题教学轻视数量关系概括、归纳、提炼的过程，而重视运用数量关系解决实际问题的应用过程。教师分类型介绍关系式，学生找类型套模型，生搬硬套是课堂上常见的现象。

张奠宙教授说过：应用题的本质就是数学建模。数学建模是重要的数学思想，我们不妨把传统的应用题教学中的数量关系式看作新课标背景下的数学模型，让学生充分经历分析、积累、抽象、归纳、概括、建模、用模的过程。

在教学过程中，我们要加强运算意义教学，以运算意义的理解为基础，进行积累和归纳，沟通数学问题与运算的联系，建立最基本的数量关系模型，提升学生分析数量关系的能力。

新课标背景下的解决问题教学不再分类型，学生解决问题时考虑的是情境中的问题与运算意义的联系，运算意义是否理解对能否有效分析数量关系起着至关重要的作用。因此，教师应加强运算意义的教学、创设具体情境，结合每一种运算逐步渗透每一种基本的数量关系，充分经历思考和体验的过程，帮助学生理解每个具体情境中的数量关系。史宁中说：“小学应用题教学只有两种类型，一种是加法，一种是乘法。”最基本的数量关系就是反映加、减、乘、除意义的数量关系。比如，在一年级认识加法运算的意义时，教师可以帮助学生结合具体的情境理解加法意义：要求总数是多少，就是把两个部分数合在一起的运算，这种运算叫做加法。

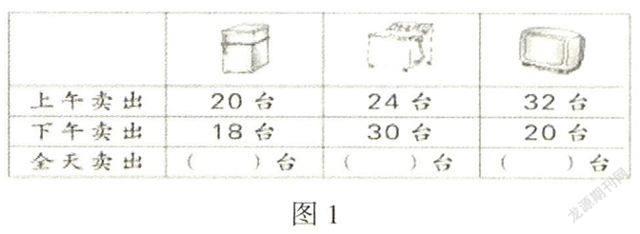
这是苏教版一年级下册的一道习题：

教师在学生审题后，引导学生进行最基本的数量关系分析：上午卖的台数+下午卖的台数=全天卖出台数。在具体情境中多次体验、感悟、积累“数学模型”实例的基础上，理解、建立它们之间的数量关系模型是“部分数+部分数=总数”，但不一定要高度概括，抽象为程式化的关系式。

在教学认识减法运算的意义时，教师可以帮助学生结合具体的情境理解减法意义，它们之间数量关系模型是：“总数—一部分数=另一部分数”。

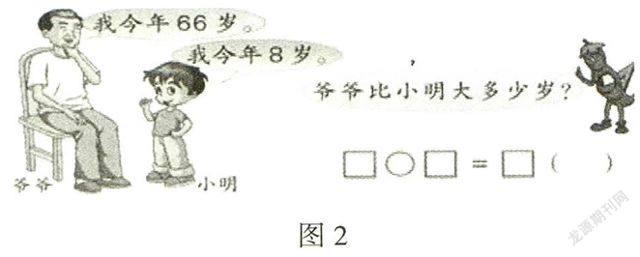
如苏教版一年级下册的一道习题：

在对两个数量进行大小比较时，教师可以帮助学生借助具体情境，用减法运算比出它们的大小，也就是从较大数中去掉与较小数同样多的部分，余下的部分即是较大数比较小数多的部分，也就是较小数比较大数少的部分，也是较大数与较小数相差的部分，数量关系模型是：“大数-小数=相差数”。

到了二年级，结合乘除法意义，在具体情境中，理解建立乘除法基本数量关系模型：“每份数×份数=总量”“大数÷小数=倍数”。

在学生结合加减法运算意义，建立最基本的数量关系模型后，教师应引导学生对加、减、乘、除各部分间的关系进行变式练习，让他们体验不同运算间的内在联系。如在苏教版二年级教学“认识除法”后教材让学生练习：

在练习中让学生体悟到乘、除法之间的互逆关系，既加深了学生对乘、除法意义的理解，又有利于学生举一反三、触类旁通。

掌握基本数量关系是解决常规问题的核心，也是以后解决非常规问题的基础。当然，在加强运算意义教学时教师要创设多元化的问题情境，多积累一些实例，为学生理解数量关系以及顺利实现“化归”提供大量的必要的原型支撑，防止情境定势。

在解决具体问题时，要沟通情境中的问题与四则运算数学意义的联系，潜移默化地渗透、理解数量关系，顺利实现对数量关系的理解和归纳，为学生解决问题能力的发展奠定基础。

二、 结合问题情境，建立常见模型

在用数学方法解决问题的过程中，教师应加强数量关系分析的指导，注重常见数量关系的抽象、概括与应用，以数量关系的有效构建提升学生分析问题和解决问题的能力。

修订后的教材同实验稿教材相比，已经明确指出部分最常见的数量关系，在学生解决问题的过程中，需要加以抽象、概括、内化、应用，最终形成自己的认识。这样，不仅能为以后解决同类型问题提供方法和策略，也为今后学习列方程解决问题打下扎实的基础，为算术思想向代数思想转变打下伏笔。

以上是苏教版四年级教材中的内容，都是在相同情境中解决相同的问题。教材中，很多运用常见数量关系的问题大量地以表格的形式呈现给学生。笔者认为，学生在解决问题之后，教师必须总结出数量关系式：“单价×数量=总价”“速度×时间=路程”。除此之外，还有不少数量关系式，如：“工作效率×工作时间=工作总量”“存款金额×利率=利息”等，在日常教学中要逐步接触、逐步渗透。这些基本关系式具有高度的概括性和广泛的应用性，教师可以用概括的语言和符号表示出来，建立数学模型，有助于培养学生抽象、概括的思维能力，感受数学抽象的美。

三、 依据基本关系，掌握复合结构

小学阶段的数量关系教学，既有简单的基本数量关系教学，也有复杂的复合数量关系教学。复合数量关系教学是小学中、高年级的重要内容，也是整个小学阶段数量关系教学的重点和核心。

由于复合数量关系是由基本数量关系组合而成的，学生要正确解决问题，必须了解复合数量关系的结构。学生对复合数量关系的形成过程、结构的把握是解决复杂问题的前提。只有学生在把握了复合数量关系是如何构成的，才能进行有意义的问题解决。

比如，学生在解决“王大伯家养鹅48只，养鸡144只，王大伯家养鹅和鸡一共多少只？”这一问题时，让其分析出数量关系式：鸡的只数+鹅的只数=养鸡鹅总只数。再对题目进行变化：“王大伯家养鹅48只，养鸡只数是鹅的3倍，王大伯家养鹅和鸡一共多少只？”让学生对两题数量关系进行比较，找出简单数量关系与复合数量关系的区别与联系，观察变化后题目中条件与问题中的另一条件有怎样的联系，让学生明白简单数量关系变换成复合数量关系的路径与方法，再进一步让学生尝试对鸡的只数进行不同的变换，让学生把数量关系简单的问题改变成数量关系复杂的问题，从而掌握数量关系复杂的问题的结构。

学生在分析、解题与编题的过程中，明白简单数量关系如何转化为复杂的数量关系，从而进一步提升他们思考与解决问题的能力。

四、 理性看待数量关系式，避免不良作用

《义务教育数学课程标准（2011年版）》背景下的数量关系教学，显然要区别于《九年制义务教育大纲》时代的数量关系教学，对原来的数量关系教学继承优点，抛弃缺点。在新课标时代背景下，我们必须注意以下几点：

一是防止无论解决什么实际问题都唯数量关系论。教师只管抛给学生数量关系式或者让学生抽象出数量关系，并进行记忆，让学生像背公式、法则似的背诵数量关系式。这不仅增加学生的学习负担，也不利于培养学生具体情况具体分析的能力。除了记忆一些特殊的数量关系式（如行程问题、购物问题等）外，多数问题可以根据具体情境来具体分析，不少问题的解决还可以通过画图、列表等策略加以解决。

二是避免抽象出的数量关系过多过细。虽然新课标教材不再将问题分类，而是将问题解决贯穿于教材各部分内容之间。但是有教师见题就抽象、提取数量关系式，使学生面对的数量关系式过多，只见树木，不见森林。我们必须紧紧依靠四则运算的意义，建立最基本的数量关系模型，找出各种数量关系与最基本的数量关系间的联系，让学生感悟到不同的数量关系本质上是一致的，复杂的数量关系都是由基本的数量关系组合而成的。

例如，许卫兵老师执教“常见的数量关系”时，借助行程问题实例启发学生悟出并建立“速度×时间=路程”的模型。在抽象出数量关系模型后，进一步学会变式运用，得出：“路程÷时间=速度”“路程÷速度=时间”。在此基础上再提升，使学生悟出“速度×时间=路程”实则为“每份数×份数=总数”，再进一步变式：“总数÷份数=每份”“总数÷每份=份数”。同时，引导学生回忆二年级的学习内容，将一系列“一乘两除”的问题归之于乘法，对众多具体的模型进行适度的生成、拓展与重塑，高度概括为一个模型：“每份数×份数=总数量”。做到了数量关系越教越简单，一通百通。

三是避免大量套模型的机械训练。由于有些问题数量关系复杂，教师为了让学生形成熟练的解题技巧和技能，进行大量题型式训练，祈盼学生能熟练地解决问题，忽视了数量关系分析过程对于促进学生思维发展的重要价值。我们应该让学生在解决问题时了解条件与问题的关系，了解复杂数量关系是如何生成的，实现数学的教育功能。

在问题解决教学中，引领学生在书本知识与现实生活联系的过程中，在从具象到抽象的过程中，让学生根据四则运算的意义、问题结构，分析数量关系。用等式、符号、语言、图形、模拟等形式表示数量关系，其关键在于让学生经历建立数量关系模型的抽象过程，经历提炼、运用的过程，在经历建模、应用过程中提高学生数学思维水平，帮助学生积累直接思考的数学经验，把丰富的体验和认识转化为自身数学抽象能力的发展和思维品质的提升，进而有效地促进学生的发展。

参考文献

[1] 中华人民共和国教育部.《义务教育数学课程标准2011版》[M].北京：北京师范大学出版社，2011.

[2] 巢洪政.数量关系的本质、作用及教学[J].江苏教育，2010（1）.

[3] 吴亚萍.复合数量关系运用的结构教学[J].小学数学教师，2008（1-2）.

[4] 吴亚萍.特殊数量关系运用的结构教学[J].小学数学教师，2009（5）.

【责任编辑：陈国庆】