水机动力无杆抽油机故障特征提取方法研究*
吕俊燕,朱春梅
(1.北京信息科技大学现代测控技术教育部重点实验室,北京 100192;2.北京信息科技大学机电工程学院,北京 100192)
0 引言
随着生产发展和技术进步,机械设备正朝着大型化、连续化、高速化、精密化、系统化和自动化方向发展。抽油机是进行油田采油作业的主要机械,结构相对复杂,所处的工作环境复杂多样,工作过程中磨损较大,存在多种因素对抽油机的正常稳定的工作造成不利的影响。一旦抽油机发生故障,则会影响抽油量,损害机身,甚至会对人的生命造成威胁。为了保持抽油机良好的技术状态和维修方面的便捷,需要对其重要参数进行全面的监测与研究。故障诊断技术应运而生,它一般分为三个部分:状态监测,分析诊断和趋势分析。对抽油机从不同的角度提取最直观、最敏感、最有用的特征信息是进行抽油机故障分析诊断的重要内容和基础。
传统小波分析能够提取抽油机的故障特征,但是它的发展基础是傅里叶变换,因此小波分析的过程中受到傅里叶变换的某些限制,并且传统小波分析对信号分解后的信号不能准确实现原始信号的重构。而提升小波变换不仅能获得与传统小波分析同样的结果,还可以实现信号在不同频带上的分离,得到不同频带的能量,该方法在时域上解决问题,算法结构简单,并且运用提升算法能改善和构造期望的小波函数和尺度,实现特定的功能。
1 提升小波与流行学习原理
1.1 提升算法与提升小波变换
传统小波分析的发展基础是傅里叶变换,因此小波分析的过程中受到傅里叶变换的某些限制,并且传统小波分析对信号分解后的信号不能准确实现原始信号的重构。而提升小波变换不仅能获得与传统小波分析同样的结果,还可以实现信号在不同频带上的分离,得到不同频带的能量,该方法在时域上解决问题,算法结构简单,并且运用提升算法能改善和构造期望的小波函数和尺度,实现特定的功能。它计算速度更快、方法更简单,而且适合于自适应、非线性、非奇异采样和整数到整数的变换[1]。
设信号序列 x(k)(0,1,2,…,k-1),(k∈R)为离散序列,提升过程按如下步骤进行:
(1)按LZ分割法将信号x(k)分为奇数序列x(2n+1)和偶序列x(2n)。

(2)用偶序列x(2n)预测奇数序列x(2n+1),预测值记为p(x(2n))。细节信息d(n)如式(2)所示。

(3)更新细节信息,记为U(d(n)),构建新的子集数据c(n)。

对序列c(n)重复式(1)~(3)的迭代运算,得到原始信号x(n)的一个多级分解。
1.2 流形学习及经典算法
1.2.1 流形及流形学习
流形(Manifold)是现代数学中拓扑学的概念,以数学中的微分流形为基础,是几何对象的总称,包括各种曲线和曲面[2]。
流形学习方法实现的是从样本数据{xi}中利用重构映射f得到{yi}。由定义可知,流形学习本质是对高维观测数据提取低维几何结构,获得内部规律。
1.2.2 拉普拉斯特征映射算法
Laplacian特征映射算法(LE)[3]作为流形学习方法中的经典已得到广泛研究,体现出诸多特殊优越性。LE算法的特点[4]是 Laplacian-Beltrami算子被运用到了LE算法中,该算子可由相邻图的加权拉普拉斯来近似,是一个被定义在切空间梯度向量上的散列函数。其算法描述如下:
首先,构造近邻图E,计算样本点间的欧氏距离,如果两个样本点xi和xj的欧式距离小于阈值ε,那么这两点间在Dij=∑jWij中可用一条边连接。
其次,选择权值。第一种方法是,若两个样本点xi和xj可以用一条边相连,则权值Wij=1,若不可以用一条边相连则为Wij=0。第二种方法是热核权赋值,若两个样本点xi和xj可以用一条边相连,则权值Wij=0。
最后,计算低维嵌入流形。转化为计算式的特征值和特征向量。

其中:Dij表示对角矩阵:

L=D-W表示拉普拉斯矩阵。得到低维流形:

2 基于提升小波和流形学习的抽油机系统故障特征提取
由于抽油机运行状态信号属于非平稳、非线性信号,表现为微弱、复合等特征。因此对抽油机系统运行状态的故障诊断也变得非常的复杂,很难对故障特征进行直接描述,寻找一种信号处理技术以及敏感特征提取方法就变得非常重要。
根据提升小波变换在降噪中的优势及LE算法的特点,提出基于提升小波和流形学习的抽油机系统故障特征提取方法,其计算流程如图1所示。

图1 抽油机系统故障识别流程
为更好的对抽油机系统的运行状态进行评估,提取了抽油机运行状态信号的时频域指标以及频域功率谱能量等指标来反应主轴系统运行状态。时域中选择了均方根值、绝对均值、最大峰值等13个指标,频域指标选择了平均频率和谱峰稳定指数,功率谱等指标,计算公式可参见文献[5]。
3 实验验证
由于抽油机系统成本高,不能人为设定故障进行故障数据采集,故需要在抽油机实验台上对常见故障进行模拟。本文采用水基动力无杆抽油机故障模拟实验台,该系统包括液压泵、动力油缸、传感器、冷却器、单向阀、溢流阀、节流阀、压力继电器、过滤器、动力液箱、油液箱等,如图2所示。在此试验台,通过调节特定行程中相应阀口的开口大小来模拟抽油机动力液管漏失、出油管阻塞、游动凡尔的漏失和堵塞、固定凡尔的漏失和堵塞、动力缸卡堵等故障状态。

图2 抽油机故障模拟实验台
使用抽油机实验台采集动力液管漏失、出油管阻塞、游动凡尔的漏失和堵塞、固定凡尔的漏失和堵塞、动力缸卡堵等故障的样本数据,采样点数为1024。
本文以各种故障的振动信号为研究对象,对采集到的振动信号进行归一化处理,获得规范化数据,然后使用提升小波变换对归一化的信号进行降噪。降噪效果如图4~8所示。
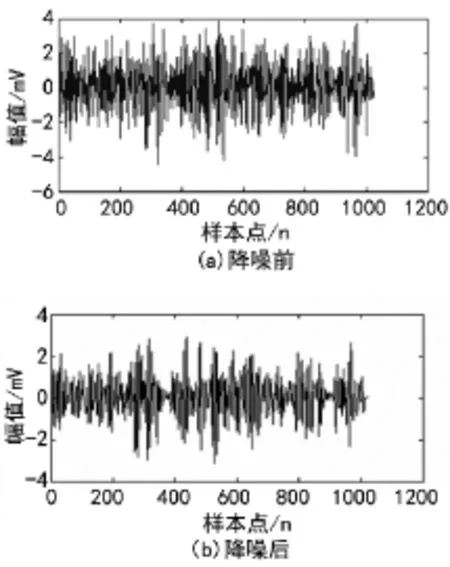
图3 抽油机正常信号降噪前后对比

图4 出油口堵塞信号降噪前后对比

图5 动力液漏失信号降噪前后对比
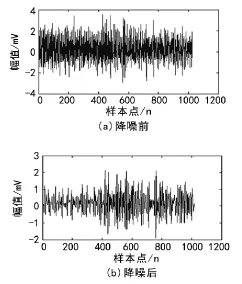
图6 固定凡尔的堵塞信号降噪前后对比

图7 游动凡尔堵塞信号降噪前后对比
运用时频域指标构造高维数据空间,选择LE算法提取高维空间中的低维流形,对比提取的低维流形,进行转子故障分类。
设定LE算法的目标维数为2,邻域点数10。定义二维流形第一主分量为x维,第二主分量为y维,运用LE算法提取,结果如图9所示。


图8 抽油机各运行状态低维流形
由二维流形图可以判断,由LE算法提取的低维流形非常集中,并且各故障状态与正常状态有明显的差异,通过观察各流形图的端点坐标、开口方向可以判断出油口堵塞、动力液漏失与凡尔堵塞问题。但固定凡尔与游动凡尔的堵塞故障所得低维流形差异不明显,是因为油液太稠或者油液内含砂等杂质都会造成游动凡尔和固定凡尔的堵塞,游动凡尔和固定凡尔的阻塞都会影响产液流量、产液压力等特征参数的变化。实验证明,LE算法能狗有效的实现故障类型的分类与识别。
4 结论
针对非平稳、非线性的振动信号,研究了基于提升小波与流形学习的故障特征提取和故障识别方法。对信号进行归一化处理,得到规范化数据,然后使用提升小波变换对归一化的信号进行降噪,运用时频域统计指标构造高维特征空间,接着运用流形学习方法提取高维空间中的低维流形,通过分析低维流形对故障进行分类和识别。上述方法能准确提取抽油机故障特征,为后续的故障分析奠定了基础。
[1] 吕善进.激光加工数控系统及状态监测技术研究[D].哈尔滨:哈尔滨工业大学,2007.
[2] 薛 坚.提升小波变换的应用与硬件实现[D].南京:南京航空航天大学,2008.
[3] Belkin M,Niyogi P.Laplacian Eigen Maps for Dimensionality Reduction and Data Representation[J].Neural Computation,2003(15):1373-139.
[4] 陈维恒.微分流形初步[M].北京:高等教育出版社,2002.
[5] 陈克兴,李川奇.设备状态监测与故障诊断技术[M].北京:科学技术出版社,1991.

