盲量子计算研究进展

王帮海,徐海茹

(广东工业大学 计算机学院，广东 广州 510006)

盲量子计算研究进展

王帮海,徐海茹

(广东工业大学 计算机学院，广东 广州 510006)

盲量子计算结合了量子密码学和量子计算的概念，使得量子能力有限甚至没有量子能力的用户可通过借助不可信的量子服务器实现量子计算，并保证其算法和数据的私密性.介绍了盲量子计算的原理及其无条件安全性，比较分析了几种通用盲量子计算协议的效率，叙述了采用基于测量技术的盲量子计算的物理实现，并对未来盲量子计算的发展和应用进行了展望.

盲量子计算； 无条件安全； 计算协议； “云”模式

量子计算(Quantum Computation)是依照量子力学理论进行的新型计算模型. 它的基础和原理以及重要量子算法为在计算速度上超越经典图灵机模型提供了可能. 量子计算的概念由IBM科学家Landauer R及Bennett C于20世纪70年代提出，当时源于对可逆计算的研究. 1985年，英国牛津大学教授Deutsch D引进量子计算线路模型和量子通用逻辑门组，提出量子图灵机的概念，使量子计算开始具备数学的基本型式[1]. 1994年，贝尔实验室Shor P W 提出了分解大数质因子的量子算法[2]，使量子计算机研究获得了实际的应用背景和新的研究动力，开启了量子计算的新阶段. 在实验上，已经在光子的偏振[3]、空腔量子电动力学等物理系统中实现了基本量子逻辑门操作，使用核磁共振[4]、离子阱[5]和线性光学等系统演示了少数量子位的简单量子计算，提出了利用强磁场作用下的2维电子液实现拓扑量子计算方案. 目前，最新的实验已经完成了3位数的因数分解[4]，我国科学家在这方面已经走在了世界的前沿[6-7].

盲量子计算(Blind Quantum Computation)是指客户端在没有足够的量子能力或量子计算能力的情况下，将量子计算任务提交给远端的量子服务商执行，但不会泄露自己的输入、输出和算法的一种量子计算模型[8-16]. 盲量子计算事实上是量子密码概念与量子数据处理的一种结合体. 众所周知，经典密码学往往是建立在某个数学难题基础上，只能达到可计算安全. 理论研究表明，盲计算的用户这种数据安全可以达到无条件安全[9]. 由于将来的量子计算资源很有可能像今天的超级计算机一样，只有少数公司、科研院所以及政府才拥有，因此，盲量子计算协议很可能会成为第一代量子计算模型[10-12].

1 盲量子计算的原理及无条件安全性

由于量子资源有限，将来在相当长一段时间内，可能只有少数机构才拥有量子计算机，普通用户的量子能力非常有限，如何让普通用户也能安全地实现量子计算将可能是一个较长时间面临的问题. 盲量子计算的目的就是为了解决这一问题. 没有量子能力或者量子能力有限的用户可借助远程的量子计算机实现量子计算，同时能保证其输入、输出数据和算法安全. 盲量子计算主要有基于线路模式和量子测量模式. 基于测量的量子计算也称为单向量子计算，两种模式具有相同的计算能力. 盲量子计算的实现模式与云计算类似，因此通常将普通用户称之为客户端，量子计算机称之为服务器[9-10].

1.1 线路模式的盲量子计算

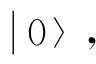
1.2 测量模式的盲量子计算

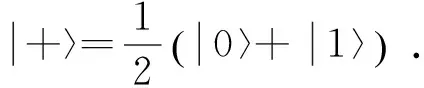
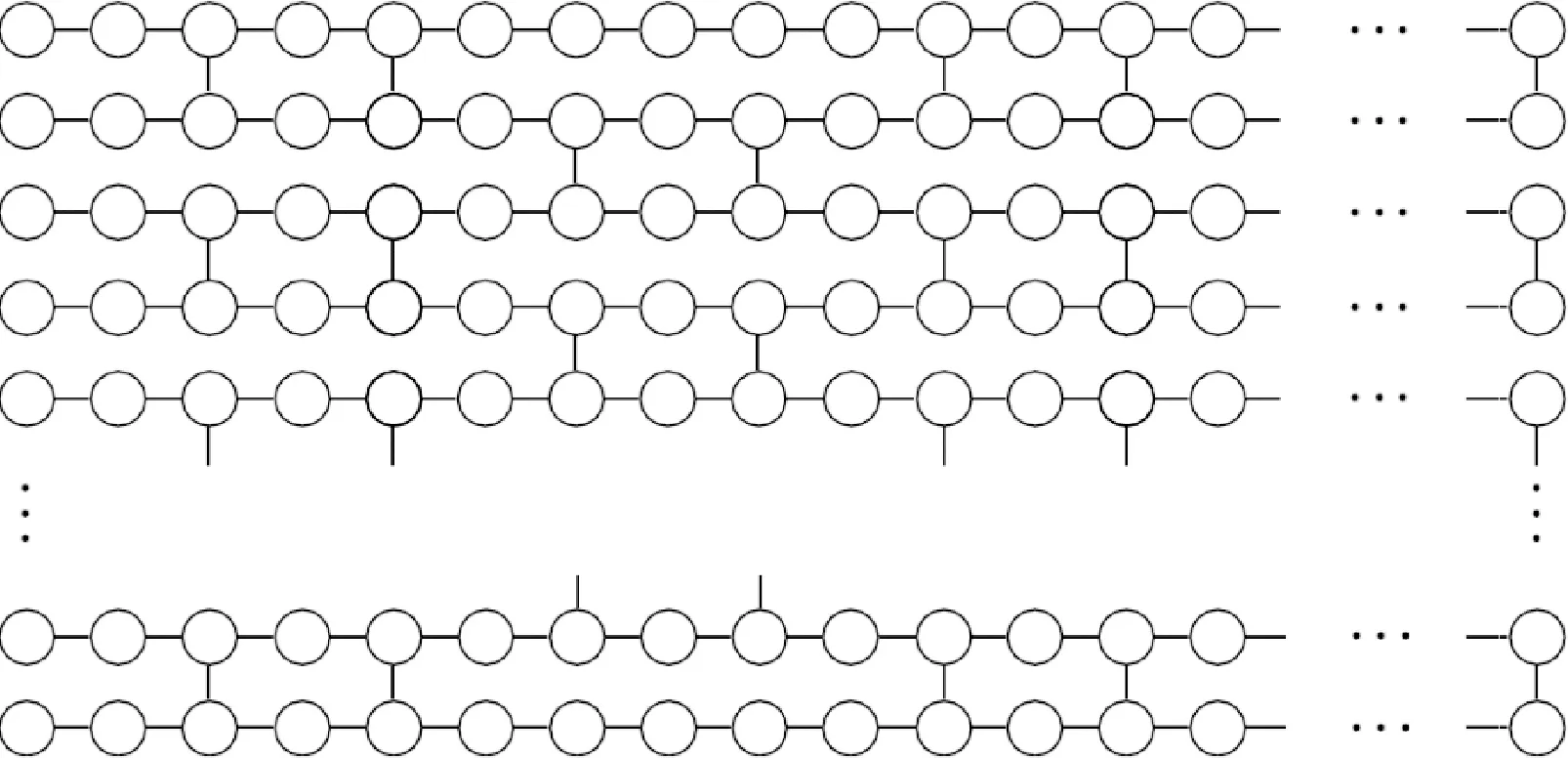
图1 Brickwork态

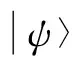
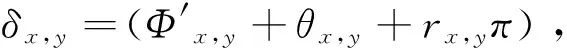
2 盲量子计算的研究现状

第一个通用盲量子计算协议[9]的提出，特别是其在物理上的实现[20]，激发了更多新的盲量子计算协议产生. 如双服务器的盲量子协议[9-10]、三服务器的盲量子协议[12]、单服务器经典客户端盲量子协议[21]，以及其他更为健壮的盲量子计算协议[23-26].

2.1 双服务器和三服务器经典客户端的通用盲量子计算协议

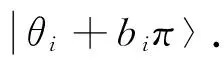
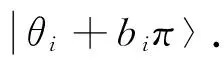
2.2 单服务器经典客户端的通用盲量子计算协议

为解决三服务器中服务器过多的问题，最近参考文献[21]提出了单服务器经典客户端的盲量子计算协议，采用了纠缠交换技术使服务器享有Bell态，客户端只需具备访问量子信道的能力. 在准备阶段，可信中心制备2n个Bell态并将Bell态的第一个量子比特发送给服务器，第二个量子比特发送给客户端，客户端随机地丢弃这些量子比特或转发给服务器. 服务器根据客户端的要求对所持有的部分量子比特进行测量，从而获得新的Bell态，但服务器并不知道每一个Bell态是由哪两个量子比特所构成. 后续的步骤同三服务器的盲量子计算协议[12]类似，原本三个服务器执行的操作在此计算协议中由一个服务器执行即可. 此外还对单服务器经典客户端的盲量子计算协议进行了进一步改进，使得客户端可以完全经典。可信中心将所有Bell态的第一个量子比特发送给服务器后，在所有Bell态的第二个量子比特中选择一部分丢弃，其余的量子比特发送给服务器，并告知客户端丢弃了哪些量子比特以及给服务器发送了哪些量子比特。客户端则可以和服务器执行单服务器经典客户端的盲量子计算协议后续的步骤来实现盲量子计算。

2.3 通用盲量子计算协议的比较及盲量子计算的模式

上述通用盲量子计算协议均采用基于测量的量子计算技术，协议具有无条件安全性，客户端不需要具备量子存储功能并且可以检测服务器是否诚实. 单服务器量子客户端协议中，客户端只需要具有制备单量子比特的能力. 双服务器盲量子计算协议中客户端完全经典，不需要具备任何量子能力，但是两个服务器之间不能进行通信，在实际的运行操作中两个量子服务器之间不能通信不太现实. 三服务器盲量子计算协议解决了服务器之间不能通信的问题，客户端只需要具备访问量子信道的能力即可. 然而为了完成量子计算，客户端需要与三个量子服务器进行通信，在实际的操作中较为困难. 单服务器经典客户端的盲量子计算协议中，客户端只需具备访问量子信道的能力，甚至如果可信中心具有一定的量子能力，客户端可以完全经典.

最近研究表明，没有第三方参与的完全经典客户端单服务器的盲量子计算不可能实现[22]，如果客户端是完全经典的，即只能操作经典数据和访问经典信道，无法实现安全的盲量子计算. 这意味着只能尽量使客户端经典，使用尽量少的量子服务器，单服务器经典客户端协议是目前最为简易可行的盲量子计算协议.

一般认为，盲量子计算以“云”模式运行，而无论是双服务器、三服务器、单服务器盲量子计算协议都需要可信中心. 可信中心在协议中的作用与今天的授权中心CA在电子商务中的作用类似，一个量子服务器可以为多个经典客户端提供量子计算服务. 因此，将来盲量子计算可能以“云+电子商务”的模式实现[21].

2.4 其他盲量子计算的研究

与通用盲量子计算采用的brickwork态不同，采用Affleck-Kennedy-Lieb-Tasaki(AKLT)作为资源态和基于测量的量子计算技术也可实现盲量子计算[23].AKLT具有资源态的冷却制备，量子计算的能量间隙保护，在双光子线性光学中资源态可以简单而有效的制备等优势. 在AKLT态上可实现单服务器和双服务器的盲量子计算[23]，而这种单服务器协议中要求客户端能够制备单量子比特，双服务器中客户端可以是完全经典的.

另外，采用Raussendor-Harrington-Goyal方法的拓扑保护方式可以实现一种容错盲量子计算[24]. 在这种方法中错误阈值为4.3×10-3相当于错误阈值为7.5×10-3的非盲拓扑量子计算. 因为在实验中实现一系列门中每个门的错误为10-3，容错的盲量子计算意味着安全云量子计算的可实现性.

在盲量子计算协议中，存在一个开放性的问题是客户端能否验证服务器的计算服务，比如计算结果是否正确等等. 基于无信号原理(no-signalingprinciple)和拓扑量子纠错码的概念，Tomoyuki还提出了针对验证盲量子计算测量结果的协议[25].

如何能判断一个盲量子计算协议是否最优的?Atul等给出了答案[26]，他们解决了要实现安全的酉操作需要多少量子通信的问题，提出了完成盲量子计算所需量子通信的上下界的技术，提出随着客户端的量子能力增强，所需的量子通信会呈指数倍的减少. 他们还计算了常见的盲量子协议所需的量子通信，如客户端可制备单量子态，可制备k-qubits的可分纠缠态，可执行常用门，有量子存储能力等不同情况所需的量子通信.

3 盲量子计算的物理实现

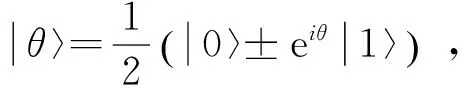
下面简略介绍一下各种量子门的物理实现.

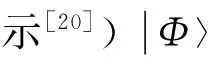
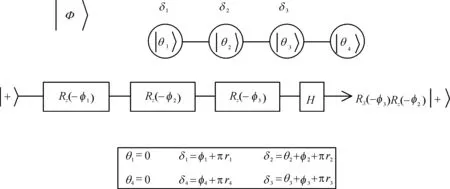
图2 X旋转门

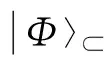
4 发展探讨与展望

盲量子计算是近10年发展起来的，从最初的辅助量子计算，实现特定函数的量子计算到通用的盲量子计算，从理论研究到实验的实现，再到实际中采用多种方法实现盲量子计算，人们围绕盲量子计算进行了多方面的研究. 目前，从客户角度，通用的单服务器经典客户端的盲量子计算协议[21]是最简易可行的方案. 该协议中只需要一个量子服务器，一个可信中心，客户端只需要具备访问量子信道的能力即可. 有学者证明没有第三方的完全经典客户端单服务器的盲量子计算不可能实现[22]，但是还有些研究人员对盲量子计算研究有信心，期待将来的研究能够消除客户端和服务器之间的量子信道，使得客户端完全经典，并且在不需要可信中心的情况下也可完成盲量子计算任务.

[1]DeutschD.Quantumtheory,theChurch-Turingprincipleandtheuniversalquantumcomputer[J].RoyalSociety, 1985, 400(1818):97-117.

[2]ShorPW.Algorithmsforquantumcomputation[C]∥Proceedingsofthe35thAnnualSymposiumonFoundationsofComputerScience.SantaFe:IEEEComputerSocietyPress, 1994:124-134.

[3]TokunagaY,KuwashiroS,YamamotoT,etal.Generationofhigh-fidelityfour-photonclusterstateandquantum-domaindemonstrationofone-wayquantumcomputing[J].PhysicalReviewLetters, 2008, 100(21):2539-2541.

[4]XuN,ZhuJ,LuD,etal.Quantumfactorizationof143onadipolar-couplingnuclearmagneticresonancesystem[J].PhysicalReviewLetters, 2012, 108(13):4089-4091.

[5]KimK，ChangMS,KorenblitS,etal.QuantumsimulationoffrustratedIsingspinswithtrappedions[J].Nature,2010, 465(7298):590-594.

[6]XuXF,BaoXH,PanJW.Demonstrationofactivefeedforwardone-wayquantumcomputingwithphoton-matterhyperentanglement[J].PhysicalReviewA, 2012, 86(5):3655-3660.

[7]CaiXD,WeedbrookC,SuZE,etal.Experimentalquantumcomputingtosolvesystemsoflinearequations.[J].PhysicalReviewLetters, 2013, 110(23):1983-1988..

[8]MorimaeT,FujiiK.BlindquantumcomputationprotocolinwhichAliceonlymakesmeasurements[J].PhysicalReviewA, 2012, 87(5),DOI:050301.

[9]BroadbentA,FitzsimonsJ,KashefiE.Universalblindquantumcomputation[C]∥Proceedingsofthe50thAnnualSymposiumonFoundationsofComputerScience.AtlantaGeorgia:IEEEComputerSocietyPress, 2009:517-526.

[10]MorimaeT,FujiiK.Secureentanglementdistillationfordouble-serverblindquantumcomputation[J].PhysicalReviewLetters, 2013, 111(2):47-89.

[11]ShengYB,ZhouL.Deterministicentanglementdistillationforsecuredouble-serverblindquantumcomputation[J].ScientificReports, 2015, 5,DOI:10.1038/srep07815.

[12] Li Q, Chan W H, Wu C, et al. Triple-server blind quantum computation using entanglement swapping[J]. Physical Review A, 2014, 89(4):2748-2753.

[13] Fitzsimons J, Kashefi E. Unconditionally verifiable blind computation[EB/OL].(2013-08-15)[2015-04-02]. http:∥arxiv.org/pdf/1203.5217.pdf.

[14] Morimae T. Continuous-variable blind quantum computation[J]. Physical Review Letters, 2012, 109(23),DOI:230502.

[15] Dunjko V, Kashefi E, Leverrier A. Blind quantum computing with weak coherent pulses[J]. Physical Review Letters, 2011, 108(20):1614-1621.

[16] Sueki T, Koshiba T, Morimae T. Ancilla-driven universal blind quantum computation[J]. Physical Review A, 2013, 87(6):4077-4082.

[17] Childs A M. Secure assisted quantum computation[J]. Quantum Information & Computation, 2005,5(6):456-466.

[18] Boykin P O, Roychowdhury V. Optimal encryption of quantum bits[J]. Physical Review A, 2000, 67(4):645-648.

[19] Polkinghorne R E S, Ralph T C. Continuous variable entanglement swapping[J]. Physical Review Letters, 1999, 83(11):2095-2099.

[20] Barz S, Kashefi E, Broadbent A, Fitzsimons J F, Zeilinger A, Walther P. Demonstration of blind quantum computing[J]. Science, 2012, 335(6066):303-308.

[21] Xu H R, Wang B H. Universal Single-Server Blind Quantum Computation for Classical Client[EB/OL]. (2014-11-12)[2015-04-02]. http:∥arxiv.org/pdf/1410.7054.pdf.

[22] Morimae T, Koshiba T. Impossibility of secure cloud quantum computing for classical client[EB/OL]. (2014-07-07)[2015-04-02]. http:∥arxiv.org/pdf/1407.1636.pdf.

[23] Morimae T, Dunjko V, Kashefi E. Ground state blind quantum computation on AKLT state[EB/OL]. (2011-06-17)[2015-04-02]. http:∥arxiv.org/pdf/1009.3486.pdf.

[24] Morimae T, Fujii K. Blind topological measurement-based quantum computation[J]. Nature Communications, 2012, 3(3):251-280.

[25] Morimae T. Verification for measurement-only blind quantum computing[J]. Physical Review A, 2014, 89(6):4085-4088.

[26] Mantri A, Perez-Delgado C A, Fitzsimons J F. Optimal blind quantum computation[J]. Physical Review Letters, 2013, 111(23):843-851.

Progress in Blind Quantum Computation

Wang Bang-hai， Xu Hai-ru

(School of Computers, Guangdong University of Technology, Guangzhou 510006, China)

Blind quantum computation that combines notions of quantum cryptography and quantum computation can fulfill quantum computation by a client with limited or even no quantum computational power with the help of an unreliable quantum server and keep the privacy of the client′s algorithm and the data. In this article, the principles and unconditional security of blind quantum computation are reviewed. And the researchers also explore several universal protocols of blind quantum computation, analyze their efficiency and introduce the physical implementation of blind quantum computation which is based on the technology of measurement-based computation. Finally, future prospect of blind quantum computation is discussed.

blind quantum computation; unconditionally secure; computation protocol; “cloud” style

2015- 04- 03

国家自然科学基金资助项目(61272013)

王帮海(1974-)，男，副教授，博士，主要研究方向为量子计算与量子信息.

10.3969/j.issn.1007- 7162.2015.03.010

O413.1

A

1007-7162(2015)03- 0051- 06