基于最小熵的流形学习排列方法

陈 静，刘 洋

(广东工业大学 1.物理与光电工程学院；2.信息工程学院，广东 广州 510006)

基于最小熵的流形学习排列方法

陈 静1，刘 洋2

(广东工业大学 1.物理与光电工程学院；2.信息工程学院，广东 广州 510006)

提出一种渐进式的排列方法：每次只是排列当前阶段交集最大的二个分片的局部坐标.该方法具有以下特点：方法简单，避免了全局排列方法中大型稀疏矩阵的特征值问题；每次排列都保证是误差最小的排列；减轻误差的积累和传播.

流形学习； 降维； 排列

流形学习作为1种非线性数据降维的方法，受到人们的广泛关注.经过多年的研究，流形学习已经形成一些有代表性的经典算法，如Isomap[1]、LLE[2-3]及其改进算法[4-6]、LE[7]、HE[8]、LTSA[9]、MVU[10]和Diffusion Map[11]等.流形学习的研究，大都围绕着这些经典算法而展开.

数学上，1个d维流形就是与d维欧氏空间局部同胚的拓扑空间，即对于流形中的每一点，都存在这个点的1个邻域，使得该邻域与d维欧氏空间的1个连通开集同胚.该邻域称为流形的1个分片，而与该分片同胚的连通开集称为分片的局部坐标，或者直接称为流形的局部坐标.流形中所有点的邻域的集合构成这个流形的1个开覆盖.如果流形是紧的，则存在流形中有限个点的邻域构成流形的有限开覆盖.根据流形的数学定义，结合数据降维的要求，对于1组从d维流形上采集的N个数据，流形学习的步骤如下：(1) 有限开覆盖：利用d维流形上采集的N个数据构造流形的有限开覆盖.(2) 局部同胚：为流形有限开覆盖中的每个分片寻找它的局部坐标，即d维欧氏空间中与分片同胚的连通开集.(3) 排列：在d维欧氏空间中排列流形的局部坐标，从而得到流形的全局坐标.

本文提出1种新的渐进式的排列方法.在渐进的过程中，这种方法每次只是把在当前阶段交集最大的2个分片的局部坐标融合为1个新的局部坐标，代替原来的2个局部坐标.整个排列的过程与霍夫曼最小熵编码的过程相似,即每次只是把在当前阶段概率最小的2个随机事件合并为1个随机事件.因此，本文把这种方法称为最小熵的排列方法(MinimumEntropyAlignment，MEA).

1 流形学习

1.1 流形学习的数学定义

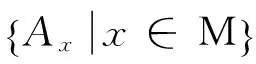
(1) 构造流形M的有限开覆盖A1,…,AM，也即构造流形M的分片；

(2) 为流形M上的每个分片Ai，在Rd中寻找一个开集Bi，使得Ai与Bi同胚，也即在 Rd中寻找Ai的局部坐标Bi，这里i=1,…,M；

(3) 在Rd中按照分片之间位置的相互关系排列它们的局部坐标，构成流形M的全局坐标.

局部同胚是各种流形共享的唯一数学特征，是高维欧氏空间中的低维流形与低维欧氏空间联系的纽带，是流形数据降维的依据.因此，本文认为，所谓流形学习可以严格定义为一种具有局部同胚保持性质的流形数据的降维方法.

1.2 流形学习算法的框架

(1) 有限开覆盖.

总而言之，流形学习算法在流形学习的这个阶段完成流形的有限开覆盖的构造为

(1)

这里Xn表示流形的1个分片，Kn表示这个分片所包含的数据点的数目，1≤nk≤N，k=1,…,Kn，M≤N表示分片的数目.

(2) 局部同胚.

为流形的每1个分片Xn构造局部同胚映射φn，于是，分片Xn的局部坐标为

(2)

目前，最常用的局部同胚映射的求解方法是PCA方法.

(3) 局部坐标排列.

LTSA建立的局部坐标Θn与全局坐标Yn的关系为

(3)

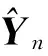
(4)

‖YWn‖2,

(5)

式(5)只是考虑1个分片的情况，如果考虑所有分片的情况，则有

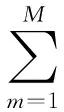
(6)

2 流形学习中的最小熵排列方法

本文提出一种新的渐进式排列方法.在渐进的过程中，这种方法每次只是把在当前阶段交集最大的2个分片的局部坐标融合为1个新的局部坐标，代替原来的2个局部坐标.整个排列的过程与霍夫曼最小熵编码的过程相似，即每次只是把在当前阶段概率最小的二个随机事件合并为1个随机事件.因此，称为最小熵的排列方法.

2.1 两个局部坐标的排列

提出的最小熵的排列方法是1种渐进式的排列方法，每次只是排列2个分片的局部坐标.文献[13]的图2清楚表达了2个分片的局部坐标排列的几何意义，但是，文献[13]的数学推导非常繁琐.本文给出1种实现排列的简单明快的数学推导.

(1) 确定变换矩阵A.

(7)

(8)

(2) 平移.

(9)

(3) 旋转和缩放变换.

(10)

(11)

(4) 排列.

(12)

2.2 最小熵排列

最小熵排列(MinimumEntropyAlignment，MEA)的步骤如下.

算法1.MEA1: 初始化.Π=Xm()m=1,…,M{},Ω=Θm()m=1,…,M{}T=m1,m2()1≤m1,m2≤M,Xm1()∩Xm2()≠φ{}2: whileM>1do3:在T中找m1,m2()使得Xm1()∩Xm2()=max 从Ω中取出Θm1()和Θm2()4: 排列Θm1()和Θm2()得到Θm() 合Xm1()和Xm2()成Xm()=Xm1()∪Xm2()5: 更新Ω:Ω=Ω-Θm1(),Θm2(){},Ω=Ω∪Θm(){}6:更新Π:Π=Π-Xm1(),Xm2(){},Π=Π∪Xm(){}7:更新T:T=T-m1,m2(){},对所有m'1,m'2()∈T,Ifm'1=m1,thenT=T-m'1,m'2(){},T=T∪m,m'2(){}Ifm'2=m2,thenT=T-m'1,m'2(){},T=T∪m'1,m(){}8: M=M-19: endwhile10: 输出Ω

最小熵排列方法具有如下特点：

(1) 最小熵排列的方法，与文献[13]和[14]的方法一样，是1种渐进式的排列方法.因此，最小熵排列的方法也具备渐进式排列方法相对于全局式排列方法的全部优点，如方法简单，避免了局部极小值的陷阱，不必求解大型稀疏矩阵的特征值问题等等.

(2) 2个分片的交集是它们局部坐标排列的依据.交集越大，排列的误差越小.最小熵排列方法每次都是选取在当前阶段交集最大的2个分片的局部坐标进行排列，因此，与文献[13]和[14]提出的方法相比，最小熵排列方法最大限度地减少了排列的误差.

(3) 减轻误差的积累和转播.正如前面所说，本文提出的排列方法与霍夫曼最小熵编码相似，而霍夫曼编码过程是1个横向优先的过程，呈现相对扁平化的结构，有助于减轻误差的积累和转播，而文献[13]和[14]提出的排列方法是1个纵向优先的方法，呈现1种树形的结构.树的每1个节点代表1个局部坐标，从树的一个节点走向另1个节点代表2个相应的局部坐标的排列，排列的误差沿着树干向下积累和传播.

3 实验结果

本文分别在人工流形数据和实际图像数据上，将提出的最小熵排列方法与6种流形学习算法(Isomap[1]、LLE[2]、LE[5]、LTSA[7]、LLI[11]和IAM[12])作比较.其中Isomap、LLE、LE、LTSA是4种经典的流形学习算法，LLI和IAM是两种基于渐进式排列的算法.需要说明的是，在本文实验中，将LLI原算法中的欧氏距离测度改为了测地距离以得到更好的结果.因为这里主要是为了比较排列的效果，所以本文的算法是用最小熵排列方法对LLI中得到的分片和局部坐标进行排列.

3.1 人工流形上的实验

本文用3个人工流形数据集来可视化地说明提出的排列方法的有效性.在以下每个实验中，对各算法的参数都作了精心选择以保证最佳的实验结果.

第1个数据集如图1(a)所示，是从嵌入在3维欧氏空间中的“Swissrollwithahole”流形上采样得到的800个数据点.Isomap的降维结果有许多空洞，还出现全局上的变形.这是因为Isomap在1个不准确的测地距离阵上进行MDS算法，导致降维结果不能很好地保持原流形的局部特性.另外，全局上的变形说明了Isomap处理非凸数据集方面的局限性.LLE的降维结果在全局上有较大的扭曲.LLE算法不能保证在原空间相距较远的两个点，降到低维空间后仍然相距很远.LE算法的结果成了曲线，显然无意义.LTSA结果看似较好，在原3维空间中的数据降到2维空间后，数据点位置的顺序关系没有发生变化.但是，流形的真实形状已经被改变了.LTSA在对数据集降维的过程中，都在某个方向上，把数据点压缩了，数据点间的真实关系没有得到保持.因为该算法只关注流形的局部几何结构，忽视了流形全局结构的保持.强加1个单位协方差矩阵约束，使得数据点之间的测地距离关系无法得到保持.LLI算法结果在中间出现断裂，这是因为渐进式的排列方法再排列的过程中会导致的排列误差的积累和传播.基于同样原因，IAM算法的结果也出现变形.本文方法的结果要优于其他6种算法，这是因为这个流形是等曲率的，这种情况下，渐进式的排列方法往往能取得较满意的效果.而且本文方法在每次排列的时候都考虑选择最小熵的2个分片进行，所以有最好的结果.

图1 Swissroll with a Hole实验

第2个数据集如图2(a)所示，采样自流形S-Curve 的1 240个数据点被分成7类.LLI和IAM的结果都有明显的断裂，本文的算法能得到较满意的结果.多类数据集几乎对所有流形学习算法来说都是个挑战[15]，本文的后续工作会在这方面继续.

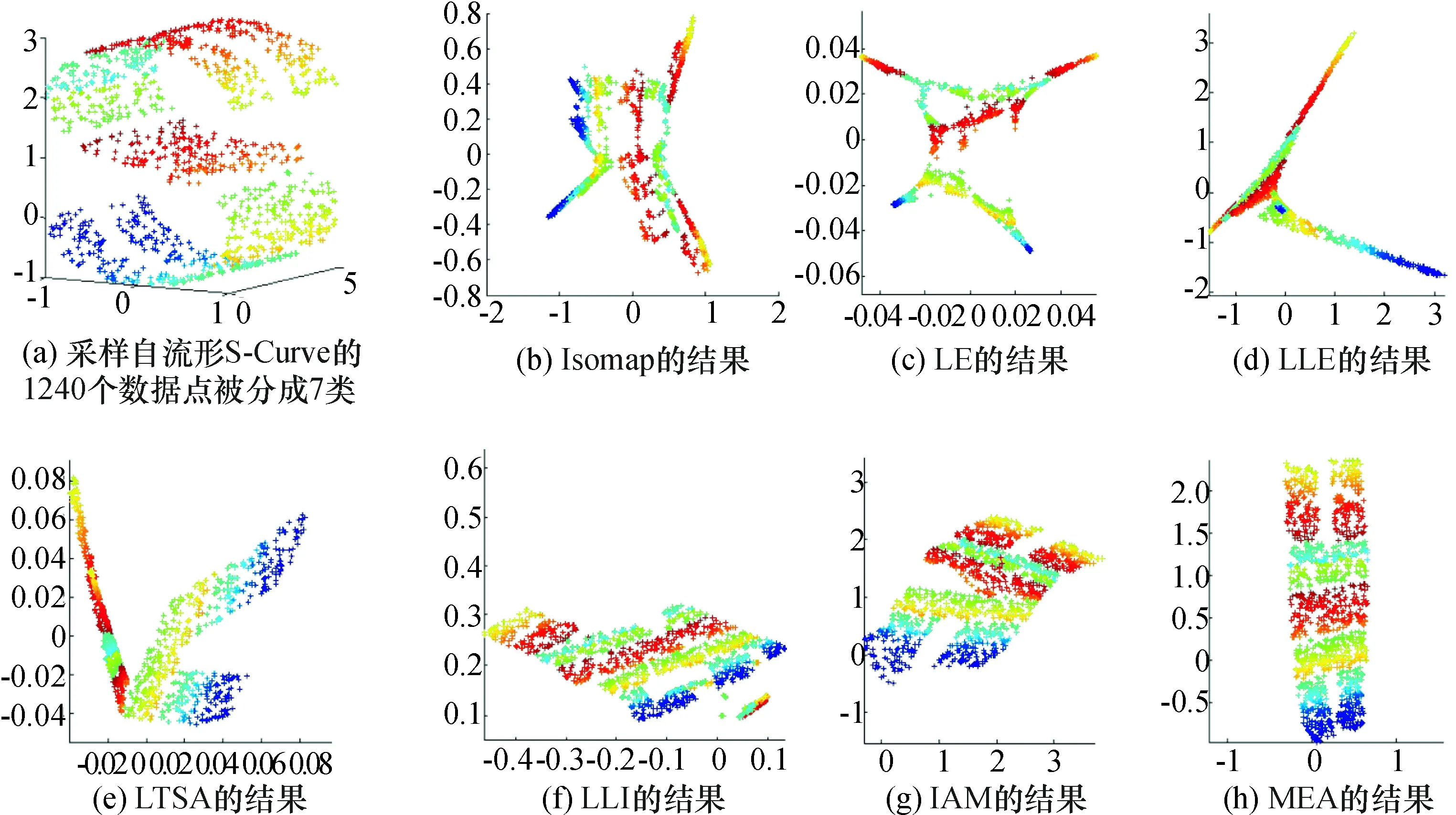
图2 多类别实验

图3是几种基于排列的流形学习方法对用不同采样密度采样自“S-curve”流形的数据点的降维结果.采样点数N分别为150、300、400、500、800.从图3可见，随着采样密度的变化，最小熵的排列方法具有最好的鲁棒性.

图3 不同采样密度采样自S-curve流形的数据点集，用4种基于排列的流形学习方法分别对其进行降维的结果

3.2 图像数据集上的实验

为了验证提出的排列方法在实际图像数据集上的效果，将该方法和现有的几种流形学习算法对USPS手写数字数据集进行降维，然后用K-均值聚类得到聚类结果，从而比较各个算法的性能.

USPS数据集包含“0”到“9”这10个手写数字，每个数字有1 100张的灰度图.每张图的大小是16×16的，看成是在D=256维空间中的1个数据点.聚类算法就是要为每个这样的数据点生成1个类标.聚类的性能可以由上述产生的类标与真实的类标的重合程度来评估.

分别取不同的聚类数K，即K=2,3,4.对每个K，随机地选择数字类别(例如K=2时，随机地从10个数字类中选择其中的2类)，并重复10次，最后的结果是取10次的平均.先用各种流形学习算法得到数据集的3维嵌入结果，然后用K-均值聚类算法进行聚类.因为聚类中心是随机选取的，所以这里运行10次K-均值算法，然后取最好的结果记录.这里需要说明的是，为了使分片之间有足够的交叠，本文让每个数据点属于4个分片，而不是原LLI中的2个分片.本文的算法也直接用上述得到的分片.表1列出了将USPS数据集用各种流形学习算法降到2维后的聚类准确率.可见3种基于渐进式排列的算法并没有比其他4种经典的流形学习方法得到更好的结果.这是因为图像数据流形不是等曲率的，渐进式排列的误差必然不会小.比较3种渐进式排列方法，本文基于最小熵的排列得到最高的聚类准确率.

表1 USPS数据集经过各算法降到2维的聚类准确率

4 结论

排列就是根据分片在高维欧氏空间中位置的相互关系，在低维欧氏空间中排列分片的局部坐标.全局和渐进式的排列方法各有千秋.渐进式的排列方法把全局排列方法中庞大的特征值问题转化为一系列简单的线性方法组求解的问题.另外，渐进式排列方法具有较强的几何特征，人们可以在渐进式排列的过程中观察流形全局坐标逐步形成的过程.但是，任何方法都有局限性.渐进式排列方法的局限性在于它主要适合像Swissroll这样曲率变化为零或曲率变化不大的流形.

现有的渐进式排列方法都是先确定1个基础局部坐标，然后逐步扩张这个基础局部坐标.这是1个纵向优先的过程，呈现树形的结构.本文提出的渐进式排列方法没有基础局部坐标的概念，每次只是排列当前阶段交集最大的2个分片的局部坐标.这是1个横向优先的过程，呈现扁平化的结构.本文提出的渐进式排列方法可以做为现有的渐进式排列方法的改进或补充.

[1] Tenenbaum J B, Silva Vin De ，Langford J C. A global geometric framework for nonlinear dimension reduction [J]. Science, 2000, 290(5500): 2319-2323.

[2] Roweis S T，Saul L K. Nonlinear dimensionality reduction by locally linear embedding [J]. Science, 2000, 290 (5500): 2323-2326.

[3] Saul L K，Rowels S T. Think globally, fit locally: Unsupervised learning of low dimensional manifolds [J]. Journal of Machine Learning Research, 2004, 4(2): 119-155.

[4] Chen J，Liu Y. Locally linear embedding: a survey[J]. Artificial Intelligence: Review, 2011, 36(1): 29-48.

[5] Sun M, Liu C, Yang J, et al. A two-step framework for highly nonlinear data unfolding [J]. Neurocomputing, 2010, 73(10-12): 1801-1807.

[6] Chen J, Liu Y. Locally Linear Embedding Based on Local Correlation [C]∥ICMV2011. Bellingham, USA: SPIE， 2011: 228-232.

[7] Belkin M，Niyogi P. Laplacian eigenmaps for dimensionality reduction and Laplacian eigenmaps for dimensionality reduction and data representation [J]. Neural Computation, 2003, 15(6): 1373-1396.

[8] Donoho D，Grimes C. Hessian Eigenmaps: new tools for nonlinear dimensionality reduction [C]∥Proceedings of National Academy of Science.Washington D C, USA: National Academy of Science，2003: 5591-5596.

[9] Zhang Z，Zha H. Principal manifolds and nonlinear dimensionality reduction via tangent space alignment [J]. SIAM Journal of Scientific Computing, 2005, 26(1): 313-338.

[10] Weinberger K Q，Saul L K. Unsupervised learning of image manifolds by semidefinite programming [J]. International Journal of Computer Vision, 2006, 70(1): 77-90.

[11] Lafon S, Keller Y，Coifman R. Data fusion and multicue data matching by diffusion maps [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(11): 1784-1797.

[12] Hou C, Zhang C, Wu Y，et al. Stable local dimensionality reduction approaches [J]. Pattern Recognition, 2009, 42(9): 2054-2066.

[13] Hou Y, Zhang P, Xu X，et al. Nonlinear dimensionality reduction by locally linear inlaying [J]. IEEE Transactions on Neural Networks, 2009, 20(2): 300-315.

[14] Zhi H, Deyu M, Zongben X，et al Incremental alignment manifold learning [J]. Journal of Computer Science and Technology, 2011, 26(1): 153-165.

[15] Meng D Y, Leung Y, Xu Z B. Passage method for nonlinear dimensionality reduction of data on multicluster manifolds [J]. Pattern Recognition, 2013, 46(8): 2175-2186.

The Minimum Entropy Alignment in Manifold Learning

Chen Jing1, Liu Yang2

(1. School of Physics and Optoelectronic Engineering; 2. School of Information Engineering, Guangdong University of Technology, Guangzhou 510006, China)

A new progressive alignment method is proposed, while only the local coordinates of the two patches with the largest intersection at the current stage of progressive alignment will be aligned into a larger local coordinate. The method has the following features: without needing to solve a large-scale eigenvalues problem and suffering from the problem of local minima; less accumulation and propagation of alignment errors.

manifold learning; dimensionality reduction; alignment

2014- 05- 13

国家自然科学基金资助项目(61305069)；广东省自然科学基金资助项目(S2013040016371)

陈 静(1980-)，女，副教授，博士，主要研究方向为机器学习.

10.3969/j.issn.1007- 7162.2015.03.008

TP 391.4

A

1007-7162(2015)03- 0039- 07