基于双私钥椭圆曲线加密的RFID身份认证协议

谢国波,郭 龙

(广东工业大学 计算机学院, 广东 广州 510006)

基于双私钥椭圆曲线加密的RFID身份认证协议

谢国波,郭 龙

(广东工业大学 计算机学院, 广东 广州 510006)

为了确保RFID系统标签数据的完整性和安全性，将双私钥椭圆曲线加密算法应用在RFID系统的身份认证协议中.选取两个椭圆双曲线基点，每个点对应一个私钥，第一个基点用来隐藏RFID系统的标签ID，防止追踪攻击；第二个基点隐藏随机数，防止重放攻击.用椭圆曲线加密算法对标签数据的加密过程代替传统协议中的哈希函数对标签数据的摘要过程，保证标签数据的完整性.结果表明，协议可以有效保护标签数据的完整性和安全性，防止伪装阅读器攻击和伪装后台服务器攻击.

RFID系统; 双私钥; 椭圆曲线加密算法

近几年，随着计算机的快速发展，计算机对数据的处理能力空前提高，为物联网技术的大规模普及奠定了坚实的基础.物联网(the Internet of Things,IOT) ：通过RFID(Radio Frequency Identification)射频识别传感器，无线通信等技术将传感器设备与计算机互联网结合，以构成一种物体与物体之间的网络[1-3].射频识别技术作为物联网的重要技术之一[4]，已成为该领域学者广泛研究的课题.

RFID系统设计的初衷是对应用完全开放.因此，攻击者可以利用其通过无线信道传输数据的特点，在身份认证和数据读取阶段对RFID系统进行攻击.大部分RFID系统因受标签限制，防伪造和抗非法读取能力非常弱，攻击者可以很容易读取或篡改标签信息，伪造标签，甚至可通过标签对所有者进行追踪.在现代大数据的环境下，标签和阅读器的计算能力和存储空间都已经不能满足设计需求，人们往往通过网络，将采集到的数据信息实时传输给计算能力较强的设备处理.比如，利用云技术处理有源标签发送云空间的数据.RFID系统所受到的安全威胁主要包括以下两方面：(1) 在阅读器和标签之间通信的过程中，身份认证和数据信息交互阶段的安全；(2) 在信息采集系统和后台处理系统通信过程中，数据传输网络的安全.

针对RFID的安全性问题,现阶段的解决方案主要集中在协议认证和信息加密两方面.文献[5]证明椭圆曲线加密算法(ECC)适合于RFID系统，文中分析了RFID系统的特点，设计出适合RFID标签的椭圆曲线密码处理器.文献[6]基于哈希函数提出一种改进的RFID双向认证协议.但是，协议没有考虑到数据完整性问题，也无法保证数据在互联网传输的安全.文献[7]提出基于椭圆曲线密码(ECC)的RFID双向认证协议，论证了椭圆加密算法在RFID上实现的可行性与安全性.但此协议不能应用到RFID标签数据信息加密过程中，攻击者很容易对标签进行跟踪攻击.文献[8]主要针对数据丢失的情况，设计了一种从云存储系统中恢复RFID标签数据的协议.不足之处是将云系统作为后台，而没有考虑传输过程中数据的安全性问题.文献[9]将椭圆曲线私钥交换协议与基于嵌入明文的加密方案相结合，将椭圆曲线加密应用在认证协议和数据信息加密两部分，保证了阅读器和标签之间数据交换的完整性，却忽略了服务器和阅读器之间的通信安全性.

本文通过分析已有认证方案，针对RFID系统的特点，提出一种基于双私钥椭圆曲线加密的RFID系统身份认证协议.考虑到标签和阅读器之间、阅读器和后台服务器之间的通信特点，提出双私钥双基点的解决方案，在数据从标签到阅读器的过程中隐藏标签ID；在数据从阅读器到后台服务器的过程中，将标签数据加密传输，解决哈希函数对信息摘要不准确的问题，保证了标签数据的完整性和安全性.本协议可以预防RFID系统中阅读器和后台服务器的伪装攻击.

1 预备知识

1.1 RFID系统

RFID系统主要由3部分组成：(1) RFID标签，包含标签ID、产品ID、产品信息以及完整性校验码；(2) RFID读取器，用于读取和写入标签数据；(3) 后台服务器，包含后台处理器和数据库两部分，分别用于处理标签数据和存放标签数据.

在RFID系统中，由于标签的存储空间和计算能力有限，标签成为整个系统中最易攻破的环节.在一些低成本的应用场合，RFID系统安全性与标签协议的成本相互制约，对标签的成本比较敏感，如何在资源有限的条件下，设计出高效算法来保护RFID系统的安全，成为设计整个系统的关键部分[10-12].

本文以表1为例进行阐述.表1为某一类产品的RFID标签包含的所有信息，标签ID是标签身份识别的唯一标识.产品号是指某一类产品的编号，但是在某些情况下几个不同标签的产品号有可能相同.文中标签产品数据DATA由D1，D2和D3组成，完整性校验码(Integrity Check Code，ICC)是由校验码生成器根据RFID标签的ID和产品的数据字段生成的校验码[8].

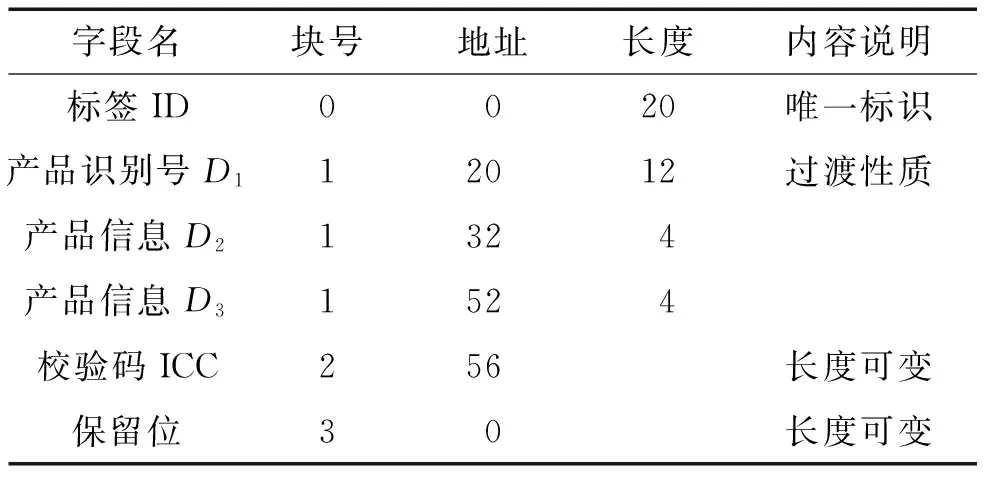
表1 RFID标签存储内容信息

1.2 ECDLP问题

椭圆曲线是有Weierstrass齐次方程确定的平面曲线[13]，表示为

y2+a1xy+a3y=x3+a2x2+a4x+a6(modp)

椭圆曲线加密算法是一种公开密钥算法，它的加密原理是基于有限区域(通常称作F域)上椭圆曲线离散对数问题的难解性，椭圆曲线在加密之前必须被离散化.椭圆曲线离散对数问题ECDLP(E11ipticCurveDiscreteLogarithms)：已知椭圆曲线E和素数p，则对于R=KG,可以通过随机数K和基点获得R，但是，反过来很难获取K和基点值.所以，在椭圆曲线身份认证协议里，往往把R作为公钥传输.图1是椭圆曲线加原理图.

图1 椭圆曲线加密算法原理图

1.3 符号标识

本文中认证协议的详细标号如表2所示.

表2 符号描述

2 双私钥安全协议

本文将双私钥的椭圆曲线身份认证应用到标签和阅读器的通信过程中，隐藏标签ID，预防了跟踪攻击；将椭圆曲线加密算法应用到阅读器和后台服务的通信过程中，预防伪装阅读器攻击和和伪装后台攻击，维护数据的完整性.文中认证协议的过程如图2所示.

图2 改进的协议

步骤1 阅读器向标签发送Query请求.

步骤2 标签收到请求后，发送基点G1和随机校验位I1到阅读器，G1点是由标签ID哈希映射产生，公式为H(G)=Hash(ID)，由于后台和标签的ID对外不可见，本步骤可以预防重放攻击和跟踪攻击.

步骤3 阅读器接收到G1和I1后，判断G1是否在椭圆曲线上，如果收到的G1在椭圆曲线上，则标签有效，发送G1和I1给后台.如果G1不在椭圆曲线上或者阅读器多次重复得到G1，则RFID系统受到了标签伪装攻击和重放攻击，结束本次认证.由于使用哈希映射，攻击者在不知道映射规则的前提下，无法反向推导出标签ID.

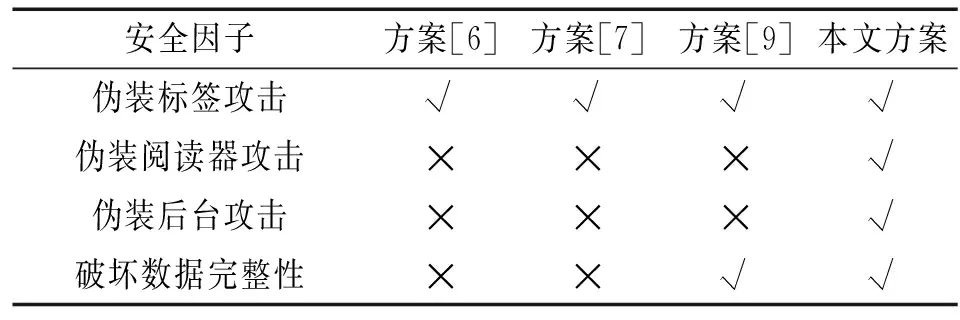
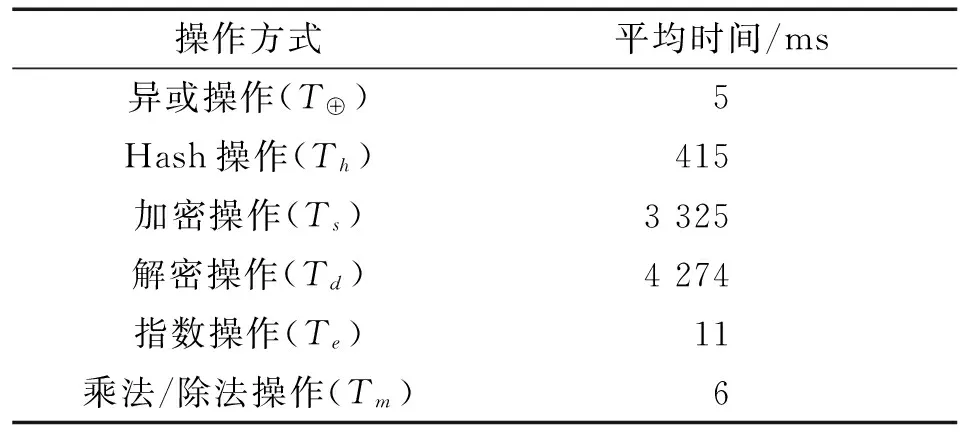
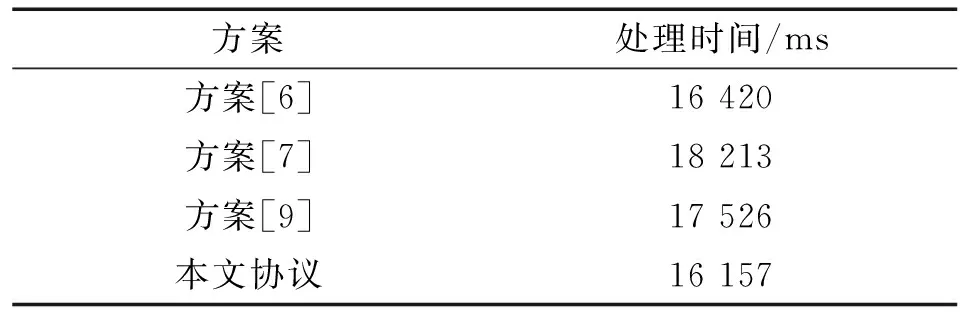
步骤4 服务器收到G1和I1后，解析G1对应的标签ID，将I1存入后台数据库相应标签ID的信息中.随机数生成器RNG随机生成k(1

步骤5 标签获得R和I1后，验证I1是否和ICC中的对应位一致，如果一致则计算得x=xR(modp)，x是公钥R的x轴坐标；生成两个签名,公式为s1=KH+xr1(modp)和s2=KH+xr2(modp)；对标签中的数据(DATA)信息D1、D2和D3，进行计算M=EKPU(ID||DATA||I),N=M⊕R，使用M主要是为了给数据加密，增强在网络传输中的安全性，防止攻击者截获数据，使用N是为了防止相同ID的标签发生数据碰撞.将五元组(x,s1,s2,M,N)发送到阅读器.

步骤6 阅读器收到后，更新一次I1记做I2，记录I2并将I2和五元组(x,s1,s2,M,N)一起发送到服务器.

步骤7 服务器先记下I2，然后判断是否认证成功，当v=x，说明R有效.证明过程如下：

(1) 计算Q(xQ,yQ)=H-1(s1×G1+s2×G2-xQ)；

(2)v≡xQ(modp);

Q=H-1(s1×G1+s2×G2-xQ)=H-1(KHG1+xr1G1+KHG2+xr2G2-xr1G1-xr2G2)=H-1(KHG1+KHG2)=KG1+KG2=R,验证成功后，对M解密DKpr(M)，判断后台数据库中相应ID存储的数据是否和ID，DATA以及I1严格一致.如果一致则判断N=M⊕R；如果相等则认证成功，向阅读器发送相应ID的标签数据以及I2.验证I2是否有效，如果有效，则发送数据给阅读器并将I2替换I1，认证过程结束；如果不同则认证失败，注销接收到的数据.

3 安全性与效率分析

3.1 安全性分析

为了保证整个RFID系统的安全性，传统协议主要预防针对RFID标签的攻击，但是攻击者同样可以攻击阅读器和劫持后台服务器.本文提出的协议针对几种常见的攻击方式有以下特点：

(1) 伪造攻击.攻击方可以假冒RFID系统的三方中的任一方进行攻击.如果RFID标签被假冒,假标签必须实现与RFID系统的阅读器进行通信，伪造出检验位I1，I2和标签ID.本协议中，当阅读器第一次请求验证时，所传输的参数是G1，此时的G1是ID的哈希映射，攻击者无法获得真实标签ID，标签中也有一个映射结果.在选定椭圆曲线情况下，二者相同的可能性很小，即使二者相同，攻击者仍需在认证阶段模拟发送五元组(x,s1,s2,M,N).在加密信息M中包含真正的标签ID，如果标签ID不能通过后台服务器的严格认证，将取消本次认证.s1，s2，R，G2都是由随机数的参与生成，不同认证过程的值都不相同.若攻击者强行编造数据，不可能通过阅读器和后台服务器的认证；如果阅读器被假冒，假阅读器无法知道标签ID就无法产生G1，无法与后台服务器通信，服务器端也不能产生G2和公钥R，标签返回的随机校验位I1失效，攻击失败；如果劫持后台服务器,假服务器产生的随机数k无效，生成的G2无效，产生错误的公钥R，错误的校验位I1，不能通过阅读器的验证.文中双私钥双基点点的设计用意就是为了防止阅读器和后台服务器被假冒攻击.

(2) 跟踪攻击.攻击者在通信过程中针对某一个标签ID进行跟踪.本协议涉及标签ID的通信过程有：① 阅读器发送Query和G1给标签，而G1是标签ID的哈希映射得来，攻击者无法通过G1获得标签ID；② 阅读器向后台服务器发送签名五元组(x,s1,s2,M,N)时，标签ID和DATA同样经过椭圆曲线加密，确保了标签ID的安全性，攻击者无法获取标签ID.综上，在本文RFID系统中，攻击者不能获得标签ID.跟踪攻击失败.

(3) 重放攻击.攻击者截获某标签和阅读器之间的通信数据，不断向标签和阅读器发送其截获的数据，企图从标签和阅读器反馈的数据中找到规律.在本协议步骤3中，初次验证成功时I1是一个随机非零值，每一个验证过程都可能不相同，在步骤4中的k，G2和R，都是直接或者间接通过随机数获得，攻击者在不能完全知道k，G2和R的情况下，将在步骤7中无法通过认证，重放攻击失败.

(4) 数据完整性攻击.传统RFID系统的椭圆曲线认证协议采用对数据进行摘要的方法.然而，这种方法不够严谨，很容易被攻破，导致数据库被攻击者修改，破坏原有数据的完整性.如果本文的协议收到数据完整性攻击，步骤7中服务器用私钥对M解密DKpr(M)，产生的ID，DATA以及I1，将在数据库中无法严格对应，后台服务器会丢掉这部分数据，保护数据的完整性.

将本文协议与传统协议比较，如表3所示.

表3 协议安全性比较

表3中√表示有效防御，×表示无效防御.由表3可知大部分协议都能抵御伪装标签攻击，本文提出的协议考虑了其他协议未考虑的情况，能抵御伪装阅读器攻击和伪装服务器攻击，保证了数据的完整性，在需要计算机网络传输数据的情况下，也能保护数据安全,大大增加了系统的安全性.

3.2 效率分析

文献[13]和文献[14]分别对身份认证方案的指数操作、双线性对操作、乘除法操作计算时间进行了测试.文献[15]基于Microsoft Visual C++ 6.0平台，在计算机硬件参数为处理器Intel(R) Penti-um(R) 4 CPU，主频2GHz，内存1G环境下，针对哈希运算、异或运算、加密解密运算的计算时间进行测试,最终得出的各类计算的平均运算时间如表4所示，表5为各方案处理时间的对比.

表4 各操作计算平均时间

表5 各方案处理时间

分析可知，在一次完整认证过程中，本文协议总的处理时间为：2Th+15T⊕+9Tm+2Tb+2Ts.其中标签计算量为：1Th+6T⊕+4Tm+1Tb.阅读器：3T⊕+1Ts.后台计算量为：1Th+6T⊕+5Tm+1Tb+1Ts. 表5将本文协议与几个典型的身份认证方案在总的处理时间上做对比，结果表明：文中所提出的双私钥椭圆曲线认证协议与大部分方案相比，在计算量上差别不大，但是本文协议具有更高的安全性.

4 结语

文中所提出的协议将传统的椭圆曲线加密应用在RFID系统认证协议中，考虑到伪装阅读器攻击和伪装服务器攻击，提出了双私钥椭圆曲线加密匿名认证协议，在没有增加计算量的情况下，大大增加了RFID系统的安全性.

[1] International Telecommunication Union.ITU Internet Reports 2005: The Internet of Things[R].2005,73(2):133-137.

[2] Gustavo R G, Mario M O, Carlos D K. Early infrastructure of an Internet of Things in Spaces for Learning [C]∥Eighth IEEE Internat-ional Conference on Advanced Learning Technol-ogies.Santander,Cantabria:IEEE,2008,27(4):381-383.

[3] Amardeo C,Sarma,J G.Identities in the future internet of things[J].Wireless Pers Commun,2009.49:353-363.

[4] 王宝云.物联网技术研究综述[J].电子测量与仪器学报,2009,23(12):34-38.

Wang B Y.Review on internat of things[J].Journal of Electronic Measurement and Instrument,2009,23(12):34-38.

[5] Yong Ki Lee,Sakiyama K,Batina L,et al.Elliptic curve based security processor for RFID[J].IEEE Transactions on Computers,2008,57(11):1514-1527.

[6] 张兵,马新新,秦志光.基于Hash运算的RFID认证协议分析和改进[J].计算机应用与研究,2011,28(11):4311-4314.

Zhang B,Ma X X, Qin Z G.Analysis and improvement of Hash-based RFID authentication protocol [J].Application Research of Computers,2011,28(11):4311-4314.

[7] 康鸿雁.一种基于ECC的RFID双向认证协议设计[J].计算机应用与软件,2012,29(9):79- 84.

Kang H Y. An ECC-based design of mutual authentication protocol for RFID[J].Computer Applications and Software,2012,29(9):79- 84.

[8] 李志科，刘竹松.基于云存储技术的RFID标签数据校验与恢复[J].广东工业大学学报,2014,31(3):137-142.

Li Z K,Liu Z S. A method of RFID tag data validation and recovery based on cloud storage technology[J].Journal of Guangdong University of Technology,2014,31(3):137-142.

[9] 吴学慧,牛志华,王潮.基于椭圆曲线密码的RFID安全协议[J].计算机工程与设计，2010,31(24):24- 29.

Wu X H,Niu Z H,Wang C.Security protocol of RFID based on elliptic curve cryptography[J]. Computer Engineering and Design,2010,31(24):24- 29.

[10] 未有彬.一种改进的RFID物联网系统加密技术[J].软件导刊,2011,10(8):24- 27.

Wei Y B.An improved encryption technology of RFID network system[J].Software Guide,2011,10(8):24- 27.

[11] 杨庚,王江涛,程宏兵,等.基于身份加密的无线传感器网络密钥分配方法[J].电子学报, 2007, 35(1): 180-185.

Yang G,Wang J T,Cheng H B,et al. A key establish scheme for WSN based on IBE and diffie-Hellman algorithms[J].Chinese Journal of Electronic, 2007, 35(1): 180-185.

[12] Tuyls P，Batina L.RFID tags for anticounterfeiting[C]∥Proceedings the Cryptographers Trackat the RSA Conference.Berlin:Springerer,2006:115-131.

[13] 刘振鹏，吴凤龙，尚开雨，等.基于TPM的云计算平台双向认证方案[J].通信学报，2012，33(22)：20- 24.

Liu Z P,Wu F L,Shang K Y,et al.Mutual authenticat-ion scheme based on the TPM cloud computing platform[J].Journal on Communications， 2012，33(22)：20- 24.

[14] Cao X, Kou W,Du X. A pairing-free identity-based authenticated key agreement protocol with minimal message exchanges [J]. Information Sciences，2010，180(15)：2895- 2903.

[15] 赵广强, 凌捷.基于双线性对和随机数的云计算环境匿名认证协议[J].广东工业大学学报,2014,31(3):67-71.

Zhao G Q，Ling J.Anonymous authentic-ation protocol based on bilinear pairing and nonce in cloud computing[J].Journal of Guangdong University of Technology,2014,31(3):67-71.

Security Protocol of RFID Based on Double Private Key Elliptic Curve Cryptography

Xie Guo-bo, Guo Long

(School of Computers, Guangdong University of Technology, Guangzhou 510006, China)

In order to ensure the safety of the RFID tag data integrity and RFID system, it is proposed that in the elliptic curve encryption double private key and double G-spot authentication protocol of RFID system, the protocol will hide tag ID in the first G point to prevent track attack. The process of Elliptic curve encryption algorithm to tag data encryption will replace the abstract process of tag data with hash function, at the same time calculate second G point. The results show that, the protocol can not only protect the integrity and security of tag data, but also prevent attacks of spoofing reader and the server.

radio frequency identification(RFID) systems; double private key; elliptic curve encryption algorithm

2015- 01- 21

广东省重大科技专项(2012A080103010);广东省重点实验室建设专项(2011A091000046);粤港关键领域重点突破项目(2012A080107007)

谢国波(1977-)，男，教授, 博士，主要研究方向为嵌入式系统、混沌保密通讯.

10.3969/j.issn.1007- 7162.2015.03.007

TP309

A

1007-7162(2015)03- 0034- 05