基于层次分析法的图书馆外包商评价指标权重确定

刘淑华

(赤峰市图书馆，内蒙古 赤峰 024000)

随着业务外包在图书馆的广泛应用，图书馆业务外包市场迅速发展，外包商数量也越来越多，对外包商的评价和选择过程也变得越来越复杂，尤其在新的经济和技术环境下，图书馆与外包商之间的合作是一种新型的、长期的、互利双赢的战略伙伴关系。因此，必须运用全面的、系统科学的评估方法或手段，对各个外包商进行对比分析，才能有效规避外包商选择失误带来的风险。本文运用层次分析法，给出了外包商评价指标权重的计算方法，以期为图书馆外包商评价与选择提供参考。

1 图书馆外包商评价指标建立

针对外包商的评价和选择，需要成立评价小组，由相关业务的馆内人员和专家组成，评价和选择过程主要由评价小组成员完成。首先，要制定出外包商评价指标体系；其次，是计算和确定评价指标权重；最后，对候选外包商进行评价和选择。在进行评价指标的选取时，要遵循全面性、科学性、简明、灵活、定性与定量相结合的原则[1]，尽量避免主观臆断。在能够全面反映外包商实际情况的前提下，评价指标应尽量精简，层级越少越好，以便于实际应用和操作。在此基础上，通过计算确定指标权重以及后续的一系列评价，才有可能选定合适的外包商。

2 层次分析法

层次分析法（Analytic Hierarchy Process，简称AHP）是美国运筹学家、匹兹堡大学教授Thomas Satty提出的一种定性与定量分析相结合的多准则、层次权重决策分析方法，被认为是简单有效的多目标决策方法，广泛应用于政治、经济、军事、科技、教育等各个领域。AHP的本质是一种决策方式，它通过对复杂问题的解析并按支配关系形成分阶层次结构，通过互相比较的方式确定各因素的重要性，然后通过人的判断确定各因素的顺序[2]。

3 运用层次分析法计算评价指标权重

用AHP解决问题，可以按如下几个步骤进行：首先，确定需要解决的问题，弄清决策所涉及的范围，所要采取的措施方案和政策，实现目标的准则、策略和各种约束条件等，建立一个多层次的递阶结构；其次，构造两两比较判断矩阵；再次，由判断矩阵计算比较元素的相对权重；最后，计算各层元素对总目标的组合权重，进行层次总排序，以确定递阶结构图中最底层各个元素在总目标中的重要程度。

下面我们通过实例对评价指标权重的计算分步骤进行说明。假设某图书馆在进行某项业务外包时已经制定了二级层次的外包商评价指标，各指标的权重计算步骤如下：第一步，建立层次递阶结构。根据已制定的外包商二级评价指标，建立如下的层次递阶结构（如表1），其中目标层即为外包商评价，一级准则层对应评价指标中的一级指标，二级准则层对应评价指标中的二级指标；第二步，构建两两比较判断矩阵。根据以上层次结构，利用Satty制定的 1-9比率标度法（表2）建立各个层次的判断矩阵。首先，请专家人员对评价体系中同一层各指标两两间的重要性等级按1-9比率标度法打分；然后，将专家的评分汇总后再发送至各位专家，收集汇总专家的修改意见后再次发送至各位专家，如此重复直至专家不再有修改意见为止。将专家最后一轮的评分情况汇总，构建两两比较判断矩阵；第三步，由判断矩阵计算比较元素的相对权重，即层次单排序。形成关系矩阵后，可根据计算矩阵的最大特征根及其对应的特征向量，确定某一类元素相对于上层某一元素的相对权重关系。常用的计算方法有和法和根法，在这里我们通过根法测算，具体步骤如下：（1）计算判断矩阵每一行元素的乘积，i=1，2，…，n(其中 n为该矩阵阶数)；（2）计算Mi的 n次方根。（3）计算矩阵的特征向量的元素值，则向量W=[W1，W2，…Wn］T即为所求的特征向量；（4）计算矩阵的最大特征值量AW的第i个元素。（5）一致性检验。

其中(AW)i为向

表1 外包商评价层次结构

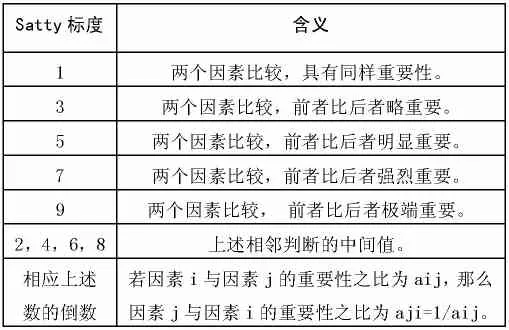
表2 Satty制定的1-9比率标度[3]

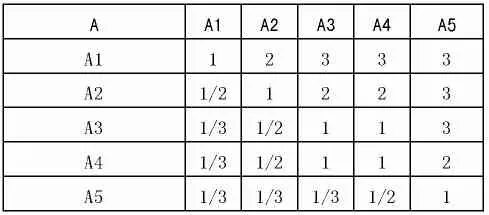
一级准则层对于目标层，两两比较判断矩阵如下（以下各表指标分值仅供参考）：

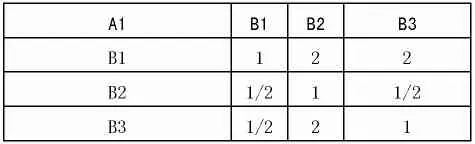
二级准则层下，对于A1，两两比较判断矩阵如下：

对于A2，两两比较判断矩阵如下：

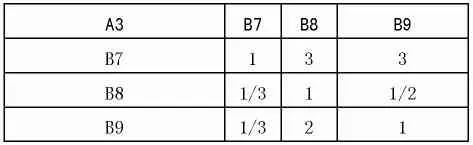
对于A3，两两比较判断矩阵如下：

对于A4，两两比较判断矩阵如下：

对于A5，两两比较判断矩阵如下：

?

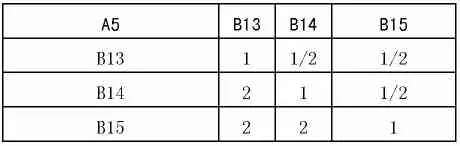
由于客观事物的复杂性和决策者认识的主观性，为确保思维的前后一致性，需要对由专家填写的判断矩阵利用一致性指标、平均随机一致性指标和一致性比率做一致性检验。若检验通过，特征向量归一化后即为权向量；若不通过，需重新构造两两比较判断矩阵。一致性检验的步骤：首先计算一致性指标。，为了度量不同阶数判断矩阵是否具有满意的一致性，需引入判断矩阵的平均随机一致性指标RI值（表3为1到15阶重复计算1 000次的平均随机一致性指标），再计算随机一致性比率。当CR〈0.10时，认为层次分析排序结果有满意的一致性，即权重系数的分配是合理的；否则，就要调整判断矩阵的元素取值，重新分配权重系数的值，直到一致性检验通过为止。

表3 1-15阶判断矩阵的平均随机性指标RI值[4]

为减少计算工作量，笔者将外包商评价一级准则层和二级准则层两两比较判断矩阵在EXCEL表格中列出，并运用EXCEL的函数功能进行相关计算如图1。

图1 利用EXCEL函数功能对判断矩阵进行计算

如图1所示，将判断矩阵在EXCEL表格中列出，可以充分利用EXCEL的函数功能，简化计算，尤其是当遇到未能达到满意一致性结果的情况，调整矩阵中各元素的取值时，CR的值也会随之自动计算得出，从而减少计算工作量。以一级准则层对于目标层A的判断矩阵为例，G4编辑为 “=PRODUCT(B4:F4)”，再通过鼠标下拉G4得到G5至G8的结果；H4编辑为“=POWER(G4,1/5)”，再通过鼠标下拉H4得到 H5 至 H8 的结果，H4 至 H8 求和得到 H9，即 H9“=SUM(H4:H8)”；I4 编辑为“=H4/H$9”，通过鼠标下拉I4得到I5至I8的结果；编辑J4“=B4*I$4+C4*I$5+D4*I$6+E4*I$7+F4*I$8”，通过鼠标下拉J4得到J5至J8的结果；编辑K4“=J4/I4”，通过鼠标下拉K4得到K5至K8的结果，K4至K8求和得到K9，即λmax的值；L8编辑为“=(K9-5)/(5-1)”，这里 n=5，求得 CI值。查表得 RI=1.12，编辑 M8为“=L8/1.12”求得 CR 值为0.0277，小于0.1，得到满意的一致性。用同样的方法进行二级准则相对于A1、A2、A3、A4、A5的判断矩阵及单排序和一致性检验[5]。求得各层次权值W如下：

一级准则层：

?

求得λmax=5.124203，CR=0.027723；二级准则层，对于A1有：

?

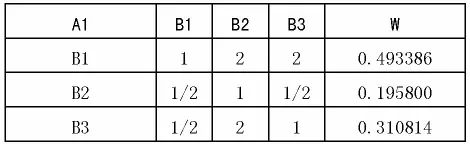
求得 λmax=9.160865，CR=0.051559；对于 A2 有：

?

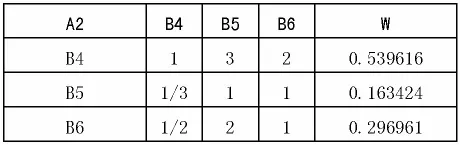
求得 λmax=9.027608，CR=0.008849；对于 A3 有：

?

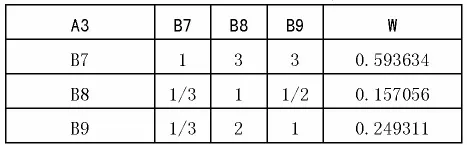
求得 λmax=9.160865，CR=0.051559；对于 A4 有：

?

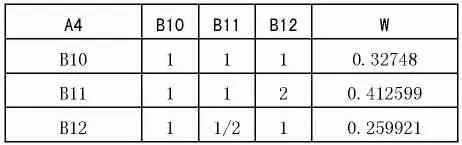
求得 λmax=9.160865，CR=0.051559；对于 A5 有：

?

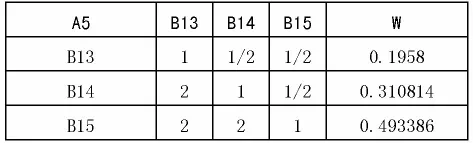
求得λmax=9.160865，CR=0.051559。根据以上计算结果，CR均小于0.1，以上矩阵具备满意的一致性。第四步，进行层次总排序。利用上层层次单排序的结果，以上层元素的组合权重为权数，计算对应本层各元素的加权和，所得结果即为该层元素的组合权重，进行层次总排序。经计算得出外包商评价A各指标的组合权重如表4：4结语

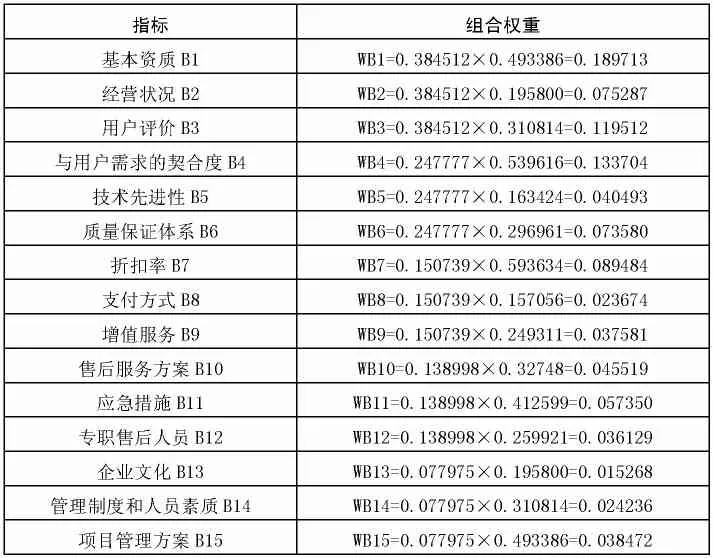
表4外包商评价A各指标的组合权重

层次分析法是建立在专家决策基础上的多维决策方法，对于判定评价指标重要程度具有逻辑关系清晰，精确度和科学性高等优点。通过构造关系矩阵,先对各指标单独进行计算,然后再进行指标间关系排序,确定各指标对于总目标的相对关系，对于构建多层次指标评价体系具有重要作用。该方法输入数据量少，并可利用办公软件进行数据处理，具有较强的可操作性。在图书馆外包商的评价和选择中，通过层次分析法除可计算得出指标权重外，也可以在专家评分的基础上计算出若干候选外包商相对于某几项指标的层次总排序而得出外包商的优先次序，从而确定最适合的外包商。

[1]李立华.基于层次分析法的高校图书馆采编外包书商评价[DB/OL].[2015-06-10].http://www.chinalibs.net/ArticleInfo.aspx?id=349640.

[2]许树柏.实用决策方法:层次分析法原理[M].天津:天津大学出版社,1988:2.

[3]董明望,周志龙.基于层次分析法的供应商选择评价系统[J].武汉理工大学学报·信息与管理工程版,2011(5):828-831.

[4]洪志国,李焱,范植华,等.层次分析法中高阶平均随机一致性指标(RI)的计算[J].计算机工程与应用,2002(12):45-47.

[5]曹茂林.层次分析法确定评价指标权重及Excel计算[J].江苏科技信息,2012(2):39-40.