开洞集装箱房屋结构纵向刚度分析

左 洋，查晓雄

(哈尔滨工业大学深圳研究生院，深圳 518055)

开洞集装箱房屋结构纵向刚度分析

左 洋，查晓雄

(哈尔滨工业大学深圳研究生院，深圳 518055)

针对目前广泛使用的集装箱房屋，研究了开洞集装箱在外荷载作用下的纵向刚度. 首先，利用蒙皮理论对其进行了力学分析，初步得出了开洞箱体刚度的计算方法，并通过算例阐述了具体的计算过程. 然后，利用非线性有限元软件 ABAQUS对其建立了有限元模型，并进行了基于开洞面积和洞口高长比的参数分析，得出了各参数对开洞箱体刚度的影响规律，并给出了相应的设计建议. 最后，进行了 5种开洞箱体刚度的试验研究，并将理论分析和有限元模拟的结果与试验数据进行了对比验证，吻合良好. 本研究不仅可为目前广泛使用的集装箱房屋提供设计和施工参考，更可为相应的规范编制提供借鉴.

集装箱房屋；轻型钢结构；纵向刚度；蒙皮理论；ABAQUS

集装箱房屋作为一种轻型钢结构被越来越多地用于房屋建筑中，集装箱用于建筑工程有许多优点并且用途广泛．首先，箱体材料可以回收利用，从而降低能源消耗，提高国家钢材战略储备．其次，箱体工厂化生产并且整体运输，在施工现场快速模块化组装，拼组成多种空间外形．另外，集装箱房屋不仅可以用于一般民用住宅，还可以大量用于抗震救灾、野外作业施工、部队军事用途等[1].

国外许多专家和学者很早便进行了集装箱房屋方面研究. Kotnik[1]介绍了世界各地的顶尖集装箱房屋项目，包括许多近期的案例，其中很多还获得国内外奖项，并通过丰富的实景图、平面图、立面图等展现了每个项目的情况．Slawik等[2]介绍了集装箱房屋的发展背景和演变过程，列举了诸多实例，从而说明了集装箱房屋在当今城市和农村中的重要作用，并给出了集装箱房屋的多种组合方式、标准以及费用．Sawyers[3]论述了集装箱房屋的加工制作过程，介绍了地基基础、箱体连接、门窗制作、室内装修等的具体施工过程，并给出了许多工程实例. Smith[4]介绍了英国住房问题和集装箱房屋的背景信息，并给出了集装箱保温模型，进行了相应的分析，得出了许多有益的结论. Gordon等[5]以大量的工程实例和图片，介绍了集装箱房屋的施工过程以及构造和内部装饰. Cao等[6]利用有限元分析了多层集装箱结构在风荷载作用下的稳定性、位移、变形以及应力，对于有加强带固定的集装箱结构提出了肯定的结论. Vinicius等[7-9]利用有限元法分析了在多种集装箱堆叠形式下，集装箱结构的振动力学性能，并用振动试验台进行了全尺寸的试验验证，为多层集装箱房屋抗震设计提供了很多有益的参考. Børvik等[10-11]首先利用铝材料设计了集装箱的围护结构，并利用有限元模拟了该保护结构在爆炸冲击荷载下的力学性能，最后利用 20,ft集装箱并配以该保护结构进行了试验研究，验证了之前有限元的分析，为集装箱房屋保护结构的制作提供了参考. Harrison[12]论述了抗爆便携结构(BRPBs)的抗爆性能以及在不同安置位置时的应用情况. Sinha等[13]提出了一个集装箱空间框架模型，按照 ISO的规范要求模拟，得到了应力和位移情况，并与试验结果进行了比较. Giriunas等[14-15]介绍了集装箱的相关标准以及集装箱房屋的基础、连接等构造情况，详细描述了集装箱有限元模型的建模过程，分析了集装箱在多种荷载形式下的刚度.

国内许多专家和学者也进行了相关方面的研究，例如，柏庭卫等[16]从建筑学的角度研究了香港集装箱建筑的基本原理、组合变化、形式类型、改造建造，并引用了大量实例说明．查晓雄[17]利用理论分析和有限元模拟的方法，研究了集装箱房屋的静动力性能、构件以及整体的优化、抗火抗震等，并用试验对其进行了验证.

然而，目前关于集装箱房屋的研究大多数是基于建筑设计的角度，仅有几篇文献是关于集装箱力学方面的性能[6-15]，但是缺乏试验验证或是局限于海运方面的研究. ISO集装箱规范制定机构 ISO/TC 104 Freight containers规范虽然提出了集装箱分类、测试等方面的标准[18-20]，但更多的是基于集装箱作为运输载体而言. 可以看出，以上研究很少涉及集装箱作为房屋结构时系统的力学性能分析，从而严重制约了集装箱房屋的应用和发展.

基于以上分析，本文首先利用蒙皮理论讨论完整及开洞波纹板的柔度计算，然后研究开洞集装箱纵向刚度的计算方法，并用算例进行解释说明．利用有限元方法研究多种开洞形式下，集装箱纵向刚度的变化规律，并提出了相应的设计施工建议．最后，进行了试验验证．

1 理论分析

集装箱房屋照片如图 1所示，主要包括 20,ft和40,ft两种型号.

图1 集装箱房屋照片Fig.1 Pictures of container buildings

20,ft集装箱及其构件组成如图 2所示，同时规定长度 L方向为纵向，宽度 W方向为横向，40,ft集装箱与其类似，集装箱的外形尺寸如表1所示. 更多集装箱信息可参见文献[18-19].

图2 20,ft集装箱及其构件组成Fig.2 20,ft container and its member composition

表1 集装箱外形尺寸Tab.1 Appearance size of container

1.1 完整波纹板柔度计算

文献[21-22]指出，完整波纹板平行于波纹方向的柔度c′的计算，可根据波纹板一个波段的变形采用能量法计算，如式(1)所示.

式中：c1′为剪切变形引起的柔度，c1′ =2 (bL+ 2bS+ bT)/(tbG)；c2′为扭转变形引起的柔度，c′ = ab2.5/(Et2.5b2)；E、G分别为钢材弹性、剪切模

2 H量；a、b分别为完整波纹板高度、长度；t为波纹板钢材厚度；K为与波纹板截面尺寸和边界连接形式有关的参数，可参考文献[17]并按式(2)计算；其余截面尺寸如图3所示.

式中xE为与波纹板波纹方向垂直的等效弹性模量，可按正交各向异性板方法取值.

对于垂直于波纹方向的柔度c的计算，可采用图4所示的柔度转换方法，令两种情况下的剪切应变θ相等．

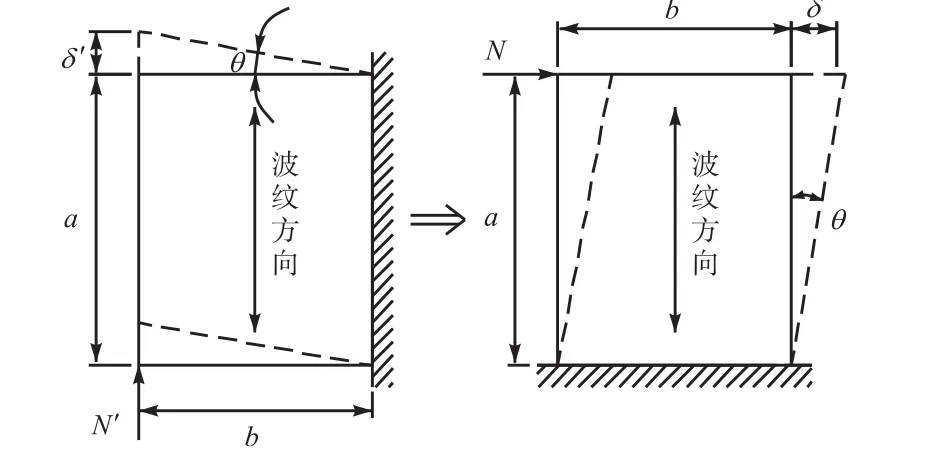
图4 柔度转换示意Fig.4 Schematic diagram of flexibility conversion

图 4中，δ′为平行于波纹方向的作用力N′所产生的剪切变形；δ为垂直于波纹方向的作用力N所产生的剪切变形；θ为波纹板所产生的剪切应变．从而有

因为

所以，由式(3)、式(4)可以求得式(5).

从而可以求得垂直于波纹方向的柔度

式中ξ为柔度转换系数，ξ = (a / b)2.

1.2 开洞波纹板柔度计算

基于之前完整波纹板柔度计算，本文将采用波纹板开洞力学模型(见图 5)，分析开洞波纹板柔度计算方法.

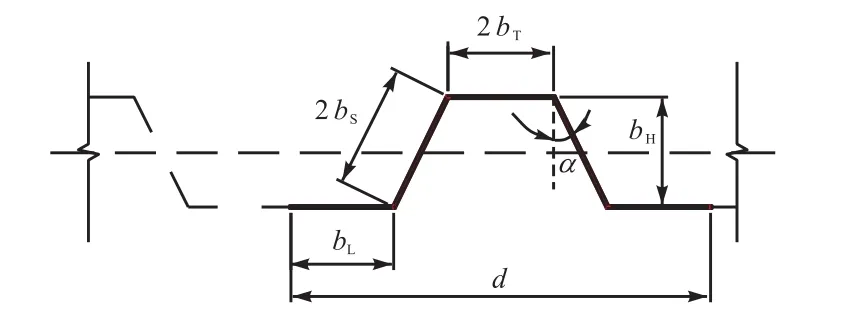
图3 波纹板截面尺寸Fig.3 Sectional dimensions of corrugated sheeting

图5 波纹板开洞力学模型Fig.5 Mechanical model of corrugated sheeting with hole

图 5中，柔性板带是指经开洞处理的波纹板部分，以洞口左右两侧为边界的竖向板带，其余竖向板带为刚性板带.lR、lG1和 lG2分别为柔性板带、刚性板带 1、2的长度；h为开洞波纹板的高度；hR1、hR2分别为洞口上、下边缘距波纹板上、下边缘的距离；NR1、NR2分别为洞口上、下部波纹板所受内力；cK′为开洞波纹板平行于波纹方向的柔度；γR、γG分别为柔性板带、刚性板带在单位荷载1作用下的剪切应变.

文献[21]指出，波纹板柔性板带所抵抗的剪力与其剩余部分波纹板高度的平方成正比，开洞后波纹板柔性板带的内力分配关系为

开洞后波纹板柔性板带与刚性板带平行于波纹方向的柔度关系可表示为式中：Rc′为柔性板带平行于波纹方向的柔度；G1c′和

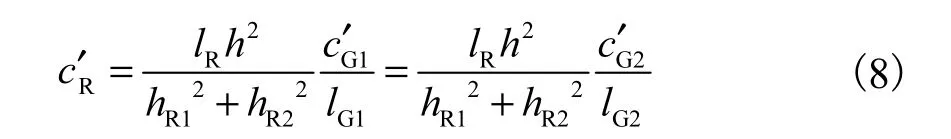
c′分别为刚性板带 1、2平行于波纹方向的柔度，可参照完整波纹板柔度，按式(1)计算. 从而可以求得开洞波纹板平行于波纹方向的柔度为

G2

利用柔度转化系数ξ，进而可以求得开洞波纹板垂直于波纹方向的柔度1.3 开洞集装箱纵向刚度计算

集装箱侧壁波纹板是箱体纵向抗侧力的主要构件，在箱体侧壁开洞的情况下，其力学性能与整箱相比将发生很大变化，在侧壁波纹板完全拆除的情况下箱体纵向刚度很小[14-15].

集装箱纵向刚度K采用箱体所受纵向外荷载作用之和2F与其作用下所产生的加载端位移Δ之比的方法来确定(见图6)，并按式(11)计算.

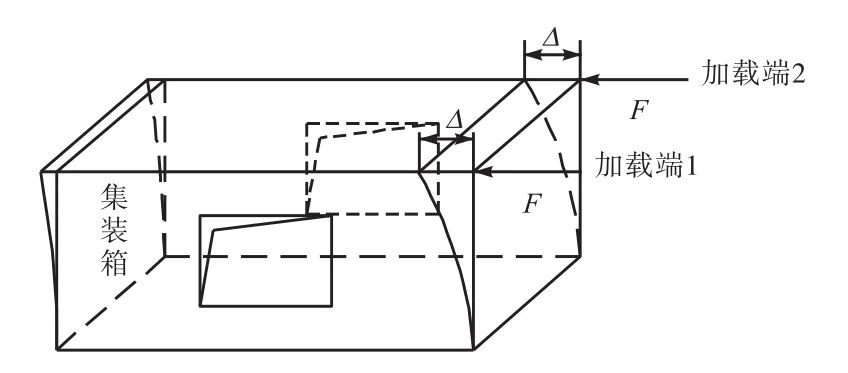
图6 集装箱刚度确定方法Fig.6 Calculation method of container stiffness

基于以上分析，在不考虑箱体框架结构作用及箱体纵向两侧非对称开洞的情况下，本文给出了开洞集装箱纵向刚度的计算方法，即

式中KC为开洞集装箱一侧的纵向柔度，其表达式为

式中：m、n分别为刚性板带、柔性板带的个数；cG′i、cR′j分别为第i、j个刚性板带、柔性板带平行于波纹方向的柔度.

1.4 试件设计

采用1个20,ft集装箱和1个40,ft集装箱，各试验项目的开洞样式如图7和图8所示，开洞尺寸如表2和表3所示，其中20,K1代表20,ft集装箱开1个洞，M代表门洞，C1代表窗1洞，其余试验编号表示类似的意义.

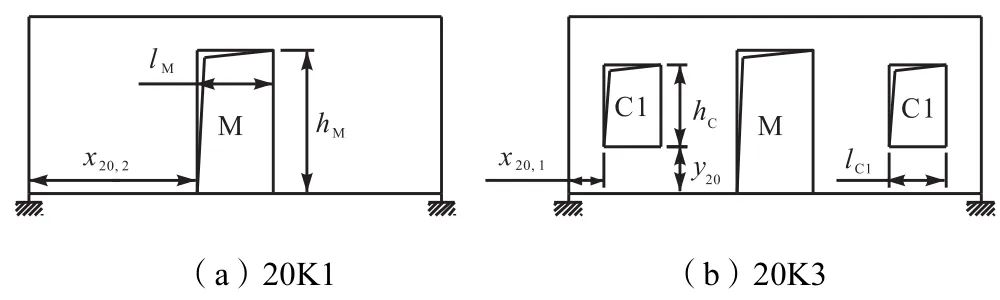
图7 20,ft集装箱开洞样式Fig.7 Style of 20,ft container with holes

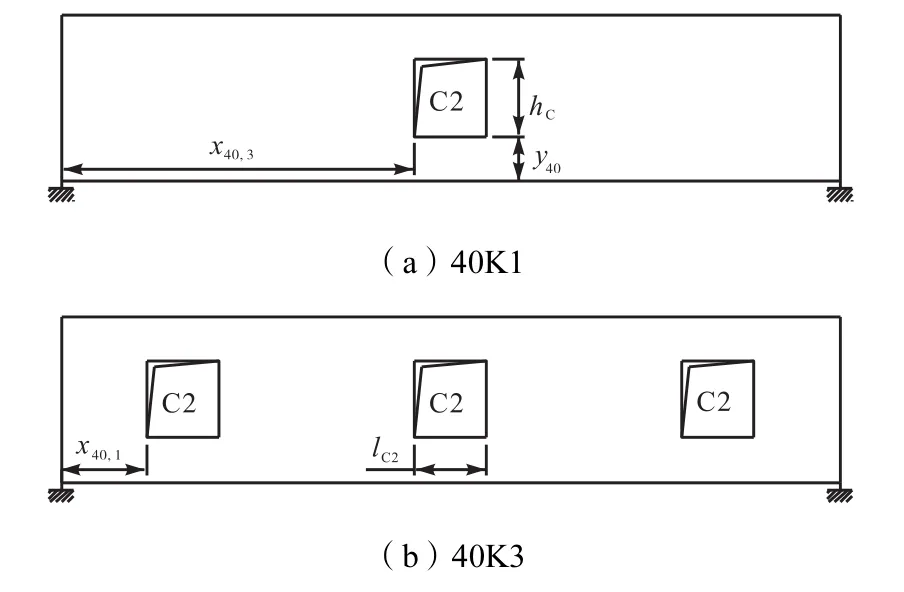
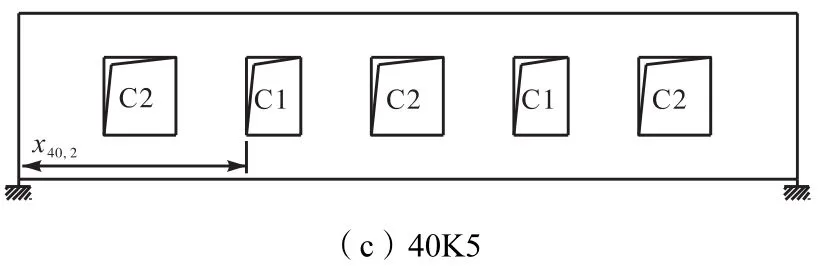
图8 40,ft集装箱开洞样式Fig.8 Style of 40,ft container with holes

表2 20,ft集装箱试验项目开洞尺寸Tab.2 Hole dimensions of experimental items of 20,ft container

表3 40,ft集装箱试验项目开洞尺寸Tab.3 Hole dimensions of experimental items of 40,ft container

1.5 开洞集装箱算例

对20K3集装箱试验项目进行刚度计算，箱体侧壁波纹板外形尺寸见表 1，开洞尺寸见表 2，箱体侧壁波纹板尺寸见图9.

图9 集装箱侧壁波纹板尺寸(单位：mm)Fig.9 Corrugated sheeting size of container side board(unit：mm)

集装箱材料参数取值：E＝200,000,MPa，G＝79,000,MPa，μ＝0.3，K＝139.82,N，ξ＝0.17.

由式(1)通过计算可以求得：图 7(b)左侧 C1的左侧刚性板带 cG′C1Z＝2.106,5×10-5,mm/N，左侧 C1的右侧刚性板带 cG′C1Y＝1.640,5×10-6,mm/N.

由式(8)和以上计算结果通过计算可以求得：左侧 C1柔性板带 cR′C1Z＝5.372,5×10-4,mm/N，M 柔性板带 cR′M＝3.678,4×10-5,mm/N.

由式(9)并由20,K3对称可以得

代入以上数据可以求得Kc′＝1.156,7×10-3,mm/N.

由式(12)并利用柔度转化系数ξ可以求得 20K3的理论刚度值为9.96,kN/mm.

2 有限元分析

为反映开洞因素对集装箱刚度的影响规律，本文将采用 ABAQUS[23]非线性有限元软件对 20,ft和40,ft两种常用型号集装箱进行相应的力学分析，研究开洞对箱体刚度的影响规律．

2.1 模型建立

对模型尺寸的选用，参考了文献[19]中的标准20,ft和40,ft集装箱.

因为集装箱各组成构件绝大部分为钢板加工而成，所以在建模时采用 3DShell单元，而对于角件采用了 3DSolid单元．对集装箱的各个部件之间采用Tie连接方式. 由于集装箱门与整体结构之间并无刚性连接，且对纵向刚度不起作用，加之尺寸和建模复杂，所以在有限元建模时没有考虑集装箱门.

对集装箱角件采用 Hex的网格单元形状，网格单元划分技术为Structured，网格单元类型为C3D8R.对集装箱顶板采用 Tri的网格单元形状，网格单元划分技术为 Free，网格单元类型为 S3. 对集装箱其他构件，由于均为钢板加工而成，所以均采用 Quad网格单元形状，网格单元划分技术为Structured，网格单元类型为S4R.

开洞集装箱有限元模型及其网格划分如图 10所示.

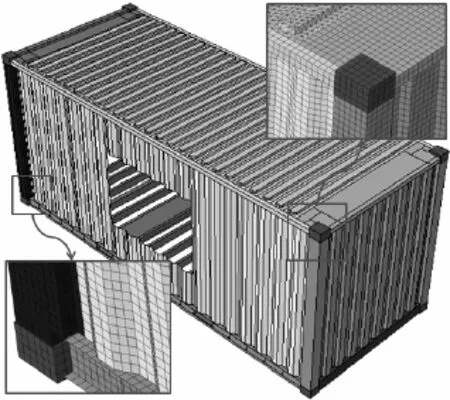
图10 集装箱有限元模型Fig.10 Finite element model of container

对有限元模型材料参数的取值是根据各构件的材性试验所得出的，如表 4所示，其中钢材密度为7.85×10-9,t/mm3. 集装箱有限元模型采用线弹性的材料本构关系，如图11所示.

集装箱有限元模型所采用的荷载为沿纵向对称集中荷载，作用在前端顶角件处；约束为 4个底角件完全固定，如图12所示.

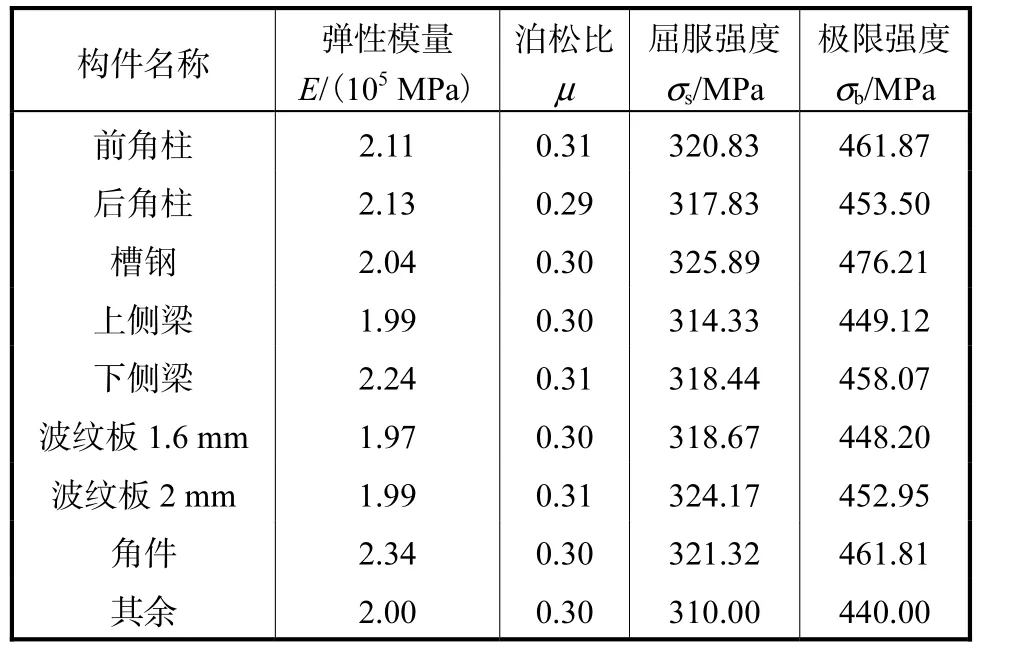
表4 集装箱有限元模型材料参数Tab.4 Material parameters of container finite element model

图11 集装箱有限元模型材料本构关系Fig.11 Material constitutive relation of container finite element model

图12 荷载和约束条件Fig.12 Condition of load and constraint

选用General通用分析步中的Static General，选用 Abaqus/Standard通用分析模块，并将 Nlgeom设为打开状态，进行静力分析.

2.2 参数分析

对20,ft和40,ft两种集装箱进行开洞参数分析，选定居中位置的矩形洞口形式，选定开洞比例η为2.5%、5%、7.5%、10%、15%、20%、30%和 50%(η=HH/h l HL)，对每种开洞比例选定洞口高长比λ( =λHH/h l)作为相应的变化参数，如图13所示.

图13 开洞比例示意Fig.13 Schematic diagram of hole proportion

通过大量的有限元模拟可以发现，各种开洞比例的箱体在洞口高长比变化时，刚度变化趋势大致相同，呈现台阶状变化，其中 5%及以上比例因洞口较大，所以较大的高长比不存在，如图14和图15所示.

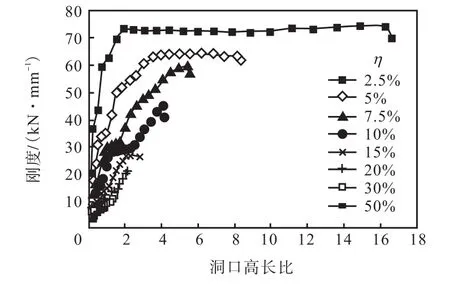
图14 20,ft集装箱开洞参数分析Fig.14 Parametric analysis of 20,ft container with holes

图15 40,ft集装箱开洞参数分析Fig.15 Parametric analysis of 40,ft container with holes

对于 20,ft集装箱(见图 14)，当开洞比例介于7.5%～20%时，箱体刚度基本呈线性变化趋势. 在同一开洞比例的情况下，随着洞口高长比的增大，箱体刚度逐渐增大. 在同一洞口高长比的情况下，随着洞口面积的增大，箱体刚度逐渐减少. 因此，设计中当开洞比例选为7.5%～20%时，应更多地选用高长比较大的洞口，以获得更大的箱体刚度.

当开洞比例小于等于 5%时，箱体刚度呈折线变化趋势. 在同一开洞比例情况下，随着洞口高长比的增大，箱体刚度逐渐增大；当洞口高长比达到一定数值后，箱体刚度基本保持不变. 在同一洞口高宽比的情况下，随着洞口面积的增大，箱体刚度逐渐减少.因此，设计中当开洞比例选为小于等于 5%时，应更多地选用洞口高长比大于3的洞口，以采用稳定的最大箱体刚度.

当开洞比例大于等于 30%时，箱体刚度很小，且变化介于 5～10,kN/mm．因此，设计中当开洞比例选为大于等于 30%时，应进行相应的洞口加固措施，以保证基本的箱体刚度.

对于40,ft集装箱(见图15)，为与20,ft集装箱进行对比，采用了相同的比例绘制，具有与20,ft集装箱开洞类似的性质，故不再赘述.

3 试验验证

为验证之前理论和有限元分析的正确性，特进行了5个开洞集装箱试验项目.

考虑到集装箱钢材为特种耐候钢Cor-Ten钢，其性能与普通建筑结构用钢有所区别，为了充分了解其性能，特进行了集装箱构件的材性试验，试验方法严格按照文献[24]执行. 拉伸试件尺寸如图16所示，材料参数见表4.

图16 拉伸试件尺寸(单位：mm)Fig.16 Tensile size of specimen(unit：mm)

3.1 试验设备和加载方案

本试验在中国国际海运集装箱(集团)股份有限公司(中集集团)试验台进行，所采用的试验设备主要包括反力架、加载装置、约束装置、力传感器、百分表、静态应变测试系统等，相关试验设备布置如图17所示．

图17 集装箱试验设备布置Fig.17 Equipment arrangement of container experiment

反力架、加载装置和约束装置分别如图 18和图19所示.

本试验主要研究开洞集装箱结构弹性阶段的纵向刚度，结构的加载方案参考了相关集装箱文献[14-15，20]．采用所加荷载使得结构最大Mises应力处最先达到材料屈服应力时的荷载值作为极限荷载，每级加载值可取极限荷载的 1/20．根据有限元计算，集装箱结构试验加载方案如表5所示.

图18 反力架Fig.18 Reaction frame

图19 加载装置和约束装置Fig.19 Loading device and constraint device

表5 集装箱试验加载方案Tab.5 Loading program of container experiment

3.2 试验结果分析

开洞集装箱试验现场照片如图20所示．

各试验项目的双侧荷载-位移曲线如图21所示，可以看出，各荷载-位移曲线较平直，说明箱体均处于弹性阶段；各荷载-位移曲线较同步，说明箱体没有较大扭转．

图20 开洞集装箱试验照片Fig.20 Pictures of experiment of container with holes

对各试验项目双侧荷载-位移曲线进行叠加处理，从而得出各试验项目的荷载-位移曲线，如图 22所示．

从图22可以看出以下3点：

(1) 各试验项目荷载-位移曲线较平直，说明其始终处于弹性阶段，从而可得出各试验项目弹性阶段的刚度值，如表6所示；

(2) 在同一型号集装箱的情况下，随着箱体开洞面积的增大，箱体刚度值逐渐减小；

(3) 对于40,ft箱体采取均匀变化开洞的形式可以看出，随着开洞面积的增大，箱体刚度值减小的速度很快，说明箱体侧壁波纹板的削弱对箱体刚度影响非常显著，如图23所示．其中，40Z为40,ft完整集装箱刚度值．

各试验项目由于只测试弹性阶段刚度，所以试验现象不明显．各试验项目刚度的理论值、有限元值和试验值对比如表7所示．

图21 双侧荷载-位移曲线Fig.21 Bilateral load-displacement curve

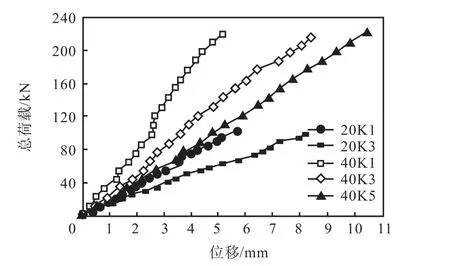
图22 各试验项目荷载-位移曲线对比Fig.22 Load-displacement curve comparison of each experimental item

表6 各试验项目刚度值Tab.6 Stiffness value of each experimental item

通过对比可以发现，理论值、有限元值均与试验值吻合较好，充分证明理论和有限元分析的正确性.

理论值较试验值小的主要原因是，没有考虑箱体端板、侧壁框架等的影响，从文献[14-15]可知这些构件对箱体纵向刚度贡献很小．20K1和 20K3与试验值相差较大，主要是因为箱体较短，箱体底部下侧梁对其约束作用较大，与蒙皮理论有一定差别，使得只有加载端处的板带参与工作，所以体现的刚度较小，就整体而言已很不明显．随着开洞数量的增多，约束越小，可以看出吻合越接近．

图23 40,ft集装箱试验项目刚度值Fig.23 Stiffness value of 40,ft container experimental items

表7 各试验项目刚度的理论值、有限元值和试验值对比Tab.7 Comparison of each experimental item stiffnessvalues of theory，finite element and experiment

有限元值较试验值大的主要原因是：①箱体约束条件为完全固定4个底角件时，试验中箱体底角件与地面支座之间实际为“锁住”，两者之间存在微小间隙，如图24所示，从而导致试验刚度值较小；②为方便测量箱体位移，在箱体顶部焊接了钢板小条，使得百分表测量钢板小条的移动，但是随着荷载的增加，前角柱随之发生弯曲变形，从而带动箱顶钢板小条向前下方移动，从而使得测量的位移值Δ变大为Δ′，刚度值随之变小，如图 25所示；③箱体或多或少存在缺陷，导致刚度减小.

图24 支座之间间隙导致误差Fig.24 Error caused by fixture device gap

图25 测量箱体位移导致误差Fig.25 Error caused by displacement measurement

4 结 论

(1) 基于蒙皮理论并利用柔度转换方法，初步得到了开洞集装箱结构纵向刚度计算式(12)并给出了计算示意.

(2) 建立了非线性集装箱有限元模型，通过开洞参数分析给出了相应的设计建议．当开洞比例选为7.5%～20%时，应更多地选用高长比较大的洞口，以获得更大的箱体刚度；当开洞比例选为小于等于 5%时，应更多地选用洞口高长比大于 3的洞口，以采用稳定的最大箱体刚度；当开洞比例选为大于等于30%时，应进行相应的洞口加固措施，以保证基本的箱体刚度.

(3) 进行了5个开洞集装箱试验项目，得到了相应的刚度值和 40,ft箱体刚度随洞口面积变化的规律，说明箱体侧壁波纹板的削弱对箱体刚度影响很大．

应该说明，本文所做的集装箱开洞方面的研究尚需完善，例如，还应考虑箱体框架的作用、洞口的形状位置、多洞口的影响因素、箱体两侧不对称开洞的问题、洞口加劲后的情况等，以上方面的研究将在后续开展.

［1］ Kotnik J. Container Architecture[M]. Barcelona：Leading International Key Services Barcelona，2013.

［2］ Slawik H，Bergmann J，Buchmeier M. Container Atlas: A Practical Guide to Container Architecture[M]. Berlin：Die Gestalten Verlag，2010.

［3］ Sawyers P. Expanded Discussion of the Method for Converting Shipping Containers into a Habitable Steel Building[M]. North Charleston：Create Space Independent Publishing Platform，2011.

［4］ Smith J D. Shipping Containers as Building Component[D]. Brighton：Department of the Built Environment，University of Brighton，2005.

［5］ Gordon A，Bergdoll B，Mclean W F，et al. Quik Build：Adam Kalkin's ABC of Container Architecture[M]. London：Bibliotheque McLean，2008.

［6］ Cao Yuan，Wang Puyong，Jin Xianlong. Dynamic analysis of flexible container under wind actions by ALE finite-element method[J]. Journal of Wind Engineering and Industrial Aerodynamics，2010，98(12)：881-887.

［7］ Vinicius A D S. Study on the Dynamic Response of Container Stacks Using Non-Linear Finite Element Analysis[D]. Tokyo：Graduate School of Frontier Sciences, The University of Tokyo, 2011.

［8］ Vinicius A D S，Kirkayak L，Suzuki K，et al. Experimental and numerical analysis of container stack dynamics using a scaled model test[J]. Ocean Engineering，2012，39：24-42.

［9］ Kirkayak L，Vinicius A D S，Suzuki K，et al. On the vibrational characteristics of a two-tier scaled container stack[J]. Journal of Marine Science and Technology, 2011，16(3)：354-365.

［10］ Børvik T，Hanssen A G，Dey S，et al. On the ballistic and blast load response of a 20 ft ISO container protected with aluminium panels filled with a local mass—PhaseⅠ：Design of protective system[J]. Engineering Structures，2008，30(6)：1605-1620.

［11］ Børvik T，Burbach A，Langberg H，et al. On the ballistic and blast load response of a 20,ft ISO container protected with aluminium panels filled with a local mass—Phase Ⅱ：Validation of protective system[J]. Engineer-ing Structures，2008，30(6)：1621-1631.

［12］ Harrison B F. Blast resistant modular buildings for the petroleum and chemical processing industries[J]. Journal of Hazardous Materials，2003，104(1)：31-38.

［13］ Sinha S C，Prakash V，Ravikumar P B，et al. Modeling and simulation of cargo containers[J]. Computers & Structures，1989，33(4)：1065-1072.

［14］ Giriunas K, Sezen H, Dupaix R B. Evaluation, modeling, and analysis of shipping container building structures[J]. Engineering Structures，2012，43：48-57.

［15］ Giriunas K A. Evaluation，Modeling，and Analysis of Shipping Container Building Structures[D]. Ohio：Department of Civil，Environmental and Geodetic Engineering，The Ohio State University，2012.

［16］ 柏庭卫，顾大庆，胡佩玲. 香港集装箱建筑[M]. 北京：中国建筑工业出版社，2004. Bai Tingwei，Gu Daqing, Hu Peiling. Hong Kong Container Architecture[M]. Beijing：China Architecture & Building Press，2004(in Chinese).

［17］ 查晓雄. 轻钢活动房计算理论——静动力、优化、性能化防火、集装箱改造房[M]. 北京：科学出版社，2011. Zha Xiaoxiong. Calculating Theory of Light Steel Prefabricated House—Static and Dynamic，Optimization，Performance-Dased Fire，Container Building[M]. Beijing：Science Press，2011(in Chinese).

［18］ ISO/TC,104. ISO 830：1999 Freight Containers-Vocabulary[S]. Geneva: International Organization for Standardization，1999.

［19］ ISO/TC 104. ISO 668：2013 Series 1 Freight Containers Classification，Dimensions and Ratings[S]. Geneva：International Organization for Standardization，2013.

［20］ ISO/TC 104. ISO 1496-1: 2013 Series 1 Freight Containers-Specification and Testing—Part 1：General Cargo Containers for General Purposes[S]. Geneva: International Organization for Standardization，2013.

［21］ Davies J M，Bryan E R. Manual of Stressed Skin Diaphragm Design[M]. New Jersey：John Wiley & Sons，Incorporated，1982.

［22］ ECCS/TC 7. N88：1995 European Recommendations for the Application of Metal Sheeting Acting as a Diaphragm—Stressed Skin Design[S]. London: European Convention for Constructional Steelwork，1995.

［23］ 庄 茁，由小川，廖剑晖，等. 基于 ABAQUS 的有限元分析和应用[M]. 北京：清华大学出版社，2009. Zhuang Zhuo，You Xiaochuan，Liao Jianhui，et al. Finite Element Analysis and Application Based on ABAQUS [M]. Beijing：Tsinghua University Press，2009(in Chinese).

［24］ ISO/TC 164. ISO 6892-1：2009 Metallic Materials-Tensile Testing—Part 1：Method of Test at Room Temperature[S]. Geneva: International Organization for Standardization，2009.

(责任编辑：樊素英)

Analysis of Longitudinal Stiffness of Container Building Structure with Holes

Zuo Yang，Zha Xiaoxiong
(Shenzhen Graduate School，Harbin Institute of Technology，Shenzhen 518055，China)

Since container buildings are widely used nowadays，this paper attempts to make a study on the longitudinal stiffness of container with holes under external load. Firstly，by applying diaphragm theory，a mechanical analysis and stiffness calculation method of container with holes were given，followed by examples to illustrate the calculation process. Then，through nonlinear finite element software of ABAQUS，a finite element model of container was established. Based on the area and aspect ratio of the hole，a parametric analysis was given to obtain the influence law of parameters on the stiffness of container with holes and some suggestions about the design were followed. Finally，five experimental studies of container with holes were conducted，and both the theoretical and finite element simulation results were compared with experimental data，which were in good agreement. The research result can offer some references not only in the design and construction of container buildings，but also in the description of relevant norms.

container building；lightweight steel structure；longitudinal stiffness；diaphragm theory；ABAQUS

TU392.5

A

0493-2137(2015)02-0167-10

10.11784/tdxbz201403070

2014-03-21；

2014-06-13.

左 洋（1983— ），男，博士研究生，wojiaozuoyang@163.com.

查晓雄，zhaxx@hit.edu.cn.