基于峰时负荷交易的有序用电机制研究
杨定立,昌健,王莉芳,董稳改,李强
(1.国网陕西省电力公司营销部,陕西西安 710048;2.西北工业大学管理学院,陕西西安 710100)
有序用电是指通过法律、行政、经济、技术等手段,采取错峰、避峰、拉路等措施,规范用电秩序,缓解季节性、时段性的电力供求矛盾的一种电力资源优化配置的管理方法。有序用电的具体方案有很多,大体分为可中断负荷[1-8]和高可靠性负荷2类。已有的研究成果都是从价格方面入手,然后建模分析,最终得到其定价方法。且现有的文献都是基于已经解除管制的国外市场,例如美国的PJM市场,其电价是自由浮动的,但我国目前尚未实现实时定价。而且国外的电力市场中,用户的高可靠性供电和断电补偿均是由电力公司提供,由于我国目前尚不具备此类政策支持,因此对电力公司的指导意义比较有限。基于以上现状,本文建立了日固定电价下的峰时负荷交易机制,通过用电企业自身对峰时负荷的交易满足用电企业对高可靠性供电和断电补偿的需求。
1 峰时负荷合同
本文考虑一个区域性的电力市场和对该市场的有序用电管理方案。将本区域内的电网企业和电厂企业视为一个电力供应商。将所有希望购买高可靠性负荷的一类厂商视为一个厂商,记为厂商1;将所有希望获得有序用电补偿的一类厂商视为一个厂商,记为厂商2。本区域的有序用电管理办法分为两类:错峰和避峰。错峰指厂商调整自身的生产时间避开用电高峰期,厂商的总用电量不变;避峰指独立电力供应商在电力系统超负荷运转的时候对厂商断电,厂商的总用电量变少。现有的电价分为峰、平、谷三类,在错峰避峰的目标下,平、谷电价可以视为同一类型,不妨统称为谷电价。因此设此时市场中仅有两类电价——峰电价和谷电价,其中峰电价大于谷电价,且峰谷电价在一天内恒定。区分峰谷电价的依据是当前电力系统安全运行能承受的负荷阈值。若电力系统的当前运行负荷值小于负荷阈值,采取谷电价;若电力系统的当前运行负荷值大于负荷阈值,采取峰电价。厂商1、2错峰避峰时有不同的成本。设峰电价为ps,谷电价为pv,且ps>pv,负荷阈值为Lc,未错峰避峰的厂商1、2均在峰电价时段生产,所需负荷分别为q1,q2,其中q1+q2>Lc。厂商1,2在用电高峰时的边际利润分别为a1,a2,在用电低谷时的边际利润分别为b1,b2,且ai>ps,bi>pv(i=1,2)。设厂商1,2在峰时的计划负荷分别为x1,x2,其中0≤x1≤q1,0≤x2≤q2。设两厂商在用电低谷时可以同时满负荷运营。当x1+x2>Lc时厂商1、2被避峰,即两者均不能在用电高峰时段生产。厂商1、2交易峰时负荷时采取先报价后交易的模式。设厂商1、2对单位峰时负荷的报价分别为f1,f2,其中厂商1希望以f1的价格买入峰时负荷y1,其中厂商2希望以f2的价格卖出峰时负荷y2,当f1=f2,y1=y2时交易发生。因为厂商1比厂商2更希望在峰时多用电,因此a1>a2。交易后厂商1、2在峰时的实际负荷分别为x1+y1,x2-y2,其中0≤y1=y2≤min(q1-x1,x2)。设厂商i每天的用电总时间为t,在高峰时期的用电时间为ti,则在低谷时期的用电时间为t-ti,厂商i的收益:(峰时边际利润-峰时电价)×峰时实际负荷×ti+(谷时边际利润-谷时电价)×谷时实际负荷×(t-ti)+峰时负荷交易净值,是ti的线性函数,该收益只在端点达到极值。因此设厂商的用电时间或者全部位于用电高峰期,或者全部位于用电低谷期。
记错峰为状态1,避峰为状态2。在报价阶段,厂商1在状态1下的收益预期为

厂商2在状态1下的收益预期为

如果用电时因为某个厂商违约而超负荷运转,厂商2将不能得到这笔交易数额,它将被原路返回到厂商1的账户。因此厂商1、2在状态2下的收益预期分别为

式中:Rij(fi,xi,yi)为策略(fi,xi,yi)厂商i在状态j下的收益。则厂商1、2在t时刻的收益矩阵见表1。
厂商i在交易前的策略为(fi,yi),即通过修改报价和待交易的负荷量来与其它厂商进行交易,此阶段其计划用电负荷xi时确定的;厂商i在交易后的策略为xi,即通过调整计划负荷改善自身的收益,此时报价fi和交易负荷yi已经确定。若R11(f1,x1,y1)>R12(f1,x1,y1),R21(f2,x2,y2)>R22(f2,x2,y2),此时厂商1,2的博弈存在一个占优均衡:(状态1,状态1),即两厂商均可以留在错峰状态下生产。以下将分析该博弈均衡可以达到的条件,厂商1、2的相应策略和电力供应商的管理方案。

表1 厂商1、2的收益矩阵Tab.1 Payoff matrix of farm 1,2
2 模型分析
厂商1、2报价时,厂商1会倾向于压低f1,厂商2会倾向于抬高f2。这两种倾向都会阻碍峰时负荷的交易,不利于电力系统的错峰。因此电力供应商在构建峰时负荷交易平台时,应当对厂商1的报价设一个下限fd,对厂商2的报价设一个上限fu。我们的目标是使各厂商能自主要想激励各厂商参与峰时负荷交易,应当确保各厂商在参与交易时的收益大于其不参与交易时的收益。设不参与交易的厂商在高峰时段会被优先限电。则各厂商参与峰时负荷交易的条件为
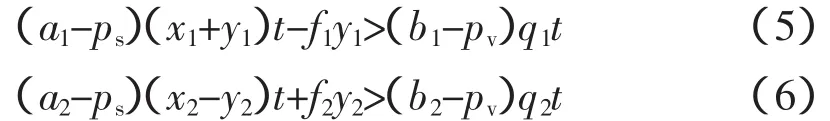
结合fi>0解出fi的范围:0
各厂商在状态1下的收益对各自交易负荷的导数如下

图1中的实线分别代表两条坐标轴和两条边界:f1=[(a1-ps)(x1+y1)-(b1-pv)q1]t/y1,即f1的上边界和f2=[(b2-pv)q2-(a2-ps)(x2-y2)]t/y2,即f2的下边界。虚线分别代表两条分类线f1=(a1-ps)t和f2=(a2-ps)t和交易条件f1=f2。其中两条分类线将平面分为了4个区域,每个区域都标注了此区域内交易负荷(y1,y2)的走向,只有当y1和y2的走向相同且f1=f2时交易才能达成,如图1中倾斜的实线段所示。此时的成交价f满足(a2-ps)t 图1 厂商1、2的报价平面f1-O-f2Fig.1 Price plane f1-O-f2of firm 1,2 若x1+x2>q1,(x1,x2)的可行域为 若x1+x2≤q1,(x1,x2)的可行域为 通过计算(10),(11)中各直线与直线x1+x2=q1,x1+x2=Lc的交点,并分析它们之间的关系,可以得到(x1,x2)的可行域如图2—图4所示。 其中,记(10)的三条直线分别为l5,l1,l2,(11)的三条直线分别为l6,l3,l4,直线x1+x2=Lc记为lc。Aij(i,j=1,…,6,c)是直线li和lj的交点。 图2 q1≤Lc时(x1,x2)的可行域之一Fig.2 Feasible region case one of(x1,x2)when q1≤Lc 图3 q1≤Lc时(x1,x2)的可行域之二Fig.3 Feasible region case two of(x1,x2)when q1≤Lc 图4 q1≤Lc时(x1,x2)的可行域之三Fig.4 Feasible region case three of(x1,x2)when q1≤Lc 厂商1、2在高峰期用电时,因为坠Ri1/坠xi>0,i=1,2,所以各厂商均倾向于增加计划负荷。如果不从外部进行调控,该博弈的均衡必会因为厂商的私自增加计划负荷而被破坏。所以需要给各厂商的负荷设定一个范围。因为Ri1是xi的单增线性函数,考虑约束条件x1+x2≤Lc,则Ri1的极值在边界x1+x2=Lc上取得。在峰时负荷交易的前提下,有 式中:f*为交易价格;y*为交易负荷,按y*的取值分为两种情形。 若Lc>q1,此时在边界x1+x2=Lc上满足x1+x2>q1,此时y*=q1-x1。消去x1得到 结合(12)可以求出此时的可行域是一条线段,其端点如下 各厂商在状态1下的总利润Rt1=R11+R21是常数依据厂商i对总利润的贡献比例坠Ri1/坠Rt1对厂商i分配利润。于是取可行域线段的中点分配厂商1、2的利润,于是相应分配给厂商1、2的负荷分别为 类似地,若Lc≤q1,此时在边界x1+x2=Lc上满足x1+x2≤q1,此时y*=x2。仿上求得可行域线段的两端点如下 则分配给厂商1、2的负荷分别为 本文建立的峰时负荷交易机制是有效的,企业收益最大化的解存在;且在用电高峰时对用电企业进行负荷定额供给不仅可以使电网安全得以保障,也可以使企业的整体收益最大化。这种交易机制的建立可以减少行政力量在电力市场的介入程度,增加市场因素在电力市场中的作用,对电力公司的计划与决策有一定的指导意义。 [1]谭忠富,谢品杰,王绵斌,等.提高电能使用效率的可中断电价与峰谷分时电价的联合优化设计[J].电工技术学报,2009,24(5):161-168.TAN Zhongfu,XIE Pinjie,WANG Mianbin,et al.The opimal desing of interating interruptible price with peakvalley time-of-use power price based on improving electricity efficiency[J].Transanctions of China Electrotechnical Society,2009,24(5):161-168(in Chinese). [2]刘兰菊.基于等微增率准则的可中断电价设计模型[J].技术经济与管理研究,2013(9):20-23.LIU Lanju.Design model of interruptible price based on equal incremental principle[J].Technoeconomics&Management Research,2013(9):20-23(in Chinese). [3]邱文锋,高志华,张勇军.基于合作分配模型的可中断电价研究[J].电气应用,2008,27(3):74-77.QIU Wenfen,GAO Zhihua,ZHANG Yongjun.Research on the outage price based on cooperative distribution model[J].Electrotechnical Application,2008,27(3):74-77(in Chinese). [4]YU C W,ZHANG S H,WANG L,et al.Analysis of Interruptible electric power in deregulated power systems[J].Electric Power Systems Research, 2007(77):637-645. [5]AALAMI H A,MOGHADDAM M P,YOUSEFI G R.Demand response modeling considering interruptible/curtailable loads and capacity market programs[J].Applied Energy,2010(87)243-250. [6]HATAMI A R,SEIFI H,SHEIKH-EL-ESLAMI M K.Hedging Risks with Interruptible Load Programs for a Load Serving Entity[J].Decision Support Systems,2009(48):150-157. [7]杨海霞,谢开贵,曹侃,等.计及指标权重的电力市场可靠性电价模型[J].电力系统保护与控制,2011,39(16):67-73.YANG Haixia,XIE Kaigui,CAO Kan,et al. Reliability electricity price model for power marker considering indicator weight[J]. Power Systerm Protection and Control,2011,39(16):67-73(in Chinese). [8]王秀丽,黄敏,陈天恩,等.计及可靠性的电力市场分时定价方法[J].电力系统自动化,2009,33(10):29-33.WANG Xiuli,HUANG Min,CHEN Tianen.Power market pricing method and reliability[J].Automation of Electric Power Systems,2009,33(10):29-33(in Chinese).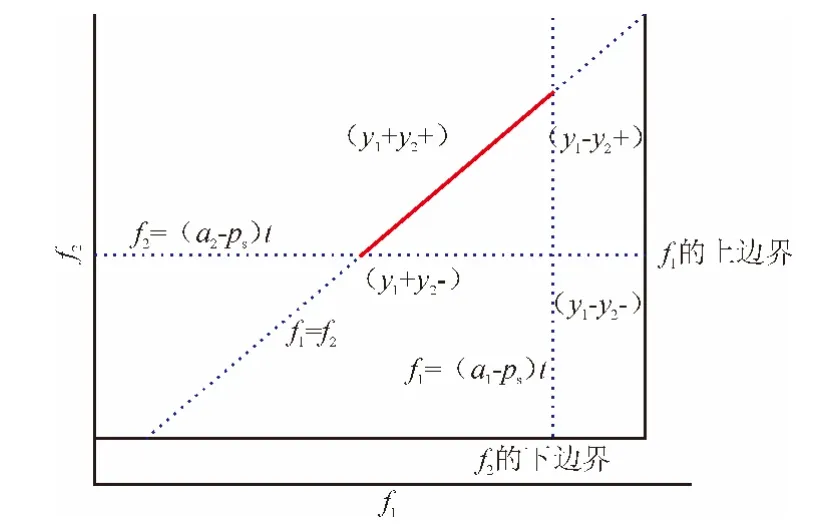

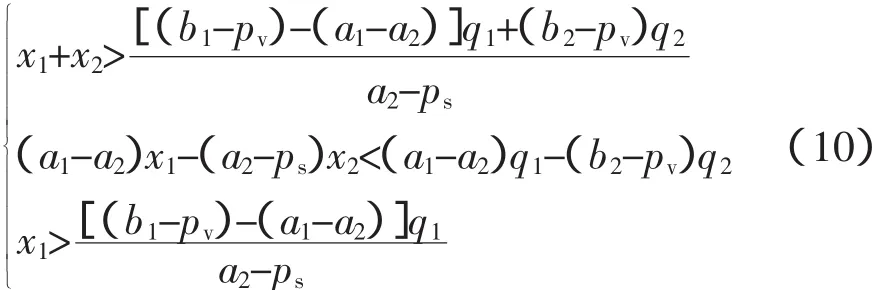
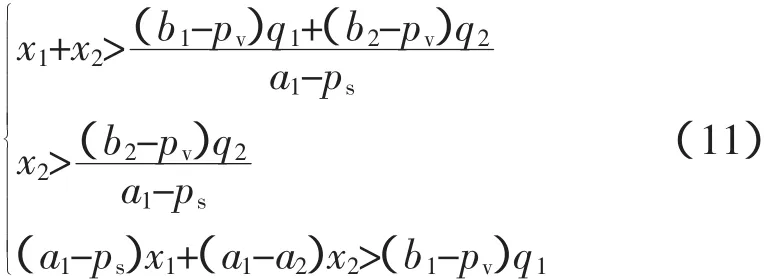




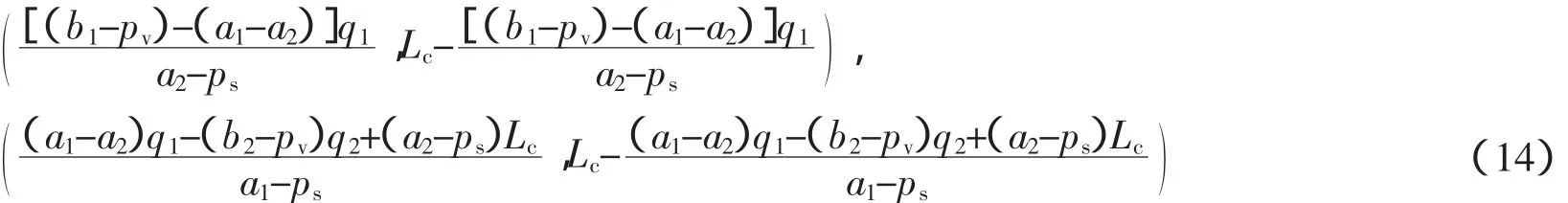



3 结语

