基于变岩电参数饱和度解释模型研究

李跃刚, 路中奇, 石林辉, 刘利锋

(1.中国石油长庆油田苏里格气田研究中心, 陕西 西安 710018;2.低渗透油气田勘探开发国家工程实验室, 陕西 西安 710018)

0 引 言

饱和度是油气藏储量计算的关键参数之一,阿尔奇公式一直是最基本、应用最普遍的饱和度计算公式,但阿尔奇公式是在中高孔隙度的纯砂岩储层假设基础上提出的,对于低孔隙度低渗透率致密储层饱和度评价存在一定的适用性问题。苏里格气田盒8段和山1段砂岩储层岩屑含量差异明显,低渗透率、低丰度的储层特征更是加大了饱和度解释的难度[1]。鉴于这种情况,本文以岩电实验数据为基础,采用岩心刻度测井技术,在不同储层测井响应特征分析基础上,提出一种应用变岩电参数计算含气饱和度的新方法,为饱和度计算精度的提高奠定了基础。

1 岩电实验分析

阿尔奇公式[2]在岩石电学研究以及电测井资料在油气储集层评价中的应用方面具有重要实际意义。该公式中存在1组重要的解释参数,包括a(岩性系数)、b(系数)、n(饱和指数)和m(胶结指数),这些参数的选取直接影响饱和度计算结果准确性,是应用阿尔奇公式评价地层含油(气)性效果好坏的关键。通常根据岩电实验可以获得a、b、m和n,对于某一特定油气藏,一般可以获得1组具有地区代表意义的特征岩电参数值[1]。

图1 苏里格气田盒8段和山1段岩样孔隙度与地层因素关系图

图1为苏里格气田盒8段和山1段岩样孔隙度与地层因素关系图。依据实验数据在双对数坐标系中,得出地层因素关系式F=4.3498/φ1.2694,由此可得a=4.349 8,m=1.269 4。与岩电参数的经典理论值(a=1,m=2)对比可知,目的层岩样表现出高a值、低m值的岩电参数特征,这是由于岩电参数经典理论值是针对中高孔隙度渗透率砂岩储层,并且忽略了泥质、导电矿物等影响因素的前提下提出的。低孔隙度低渗透率致密砂岩储层的导电特性异常复杂,简单地将实验得到的岩电参数应用于阿尔奇公式则极有可能造成解释精度的降低[3-4]。

对于苏里格气田盒8段和山1段储层,通过实验得到的固定岩电参数只是岩石样本特征的平均响应值,难以反映不同储层特征的差异性,为饱和度的精细解释造成较大的困扰。

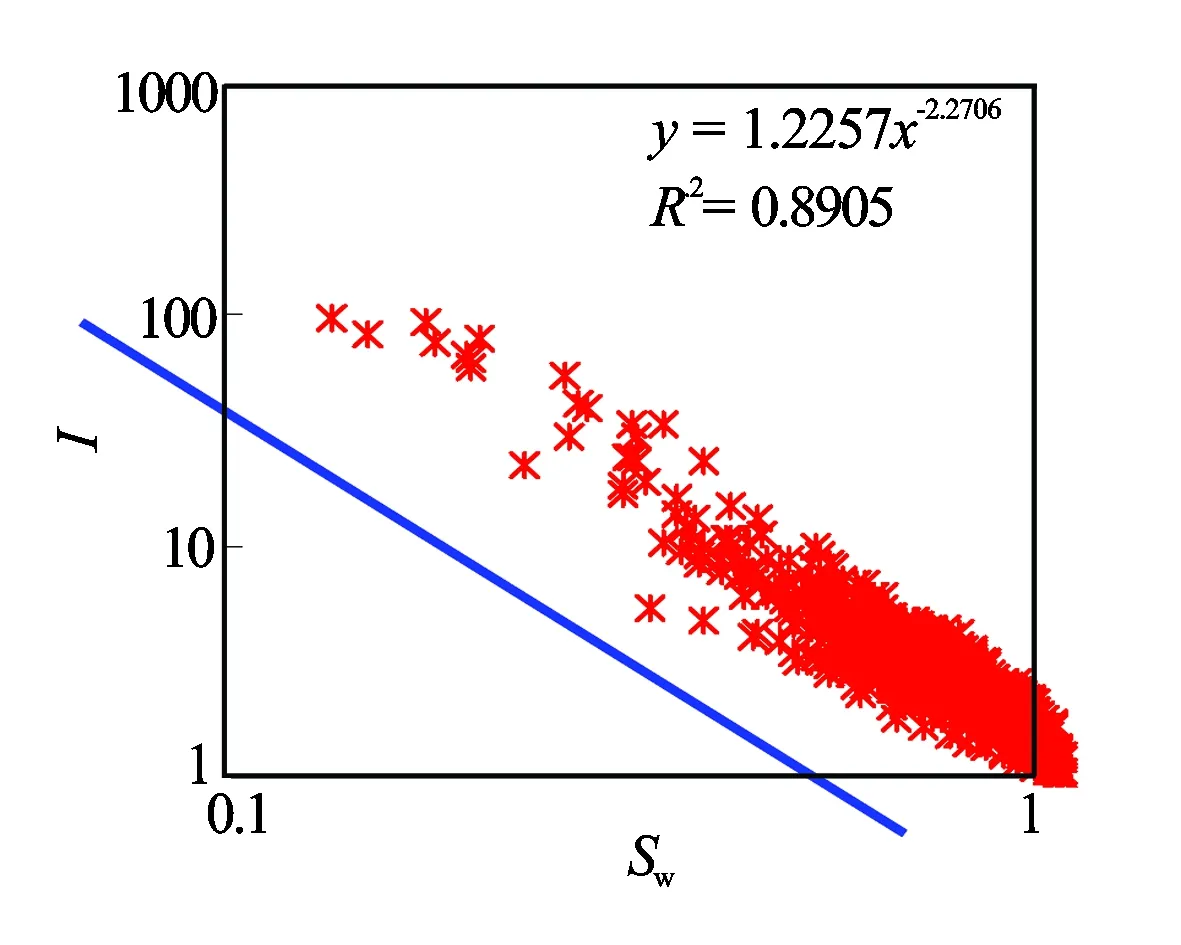
图2 苏里格气田盒8段和山1段岩样电阻率增大率与含水饱和度关系图

2 岩电参数优化

岩电参数是岩性、物性、润湿性、饱和度和孔隙结构等影响因素的综合响应[5-8],固定的岩电参数值在复杂储层差异性表征方面存在一定的局限性。在计算饱和度时,难免会存在一定缺陷。基于此,提出一种岩电参数优化方案,旨在进一步提高饱和度的计算精度。

2.1 岩电参数a、m优化方法

地层因素F定义为100%含水岩石电阻率与地层水电阻率的比值。假设当孔隙度为1时,可以推出地层因素F等于1。将该组参数与实际岩电资料数据进行交会图分析(见图3),得到地层因素计算模型对比图1和图3分析可知,这种处理方式的优点不仅在于相关系数的提高,更重要的是,可以通过孔隙度直接得到连续的地层因素值,避免了确定岩电参数a、m后再结合孔隙度计算地层因素的繁琐步骤,达到了减少变量降低计算误差的目的。

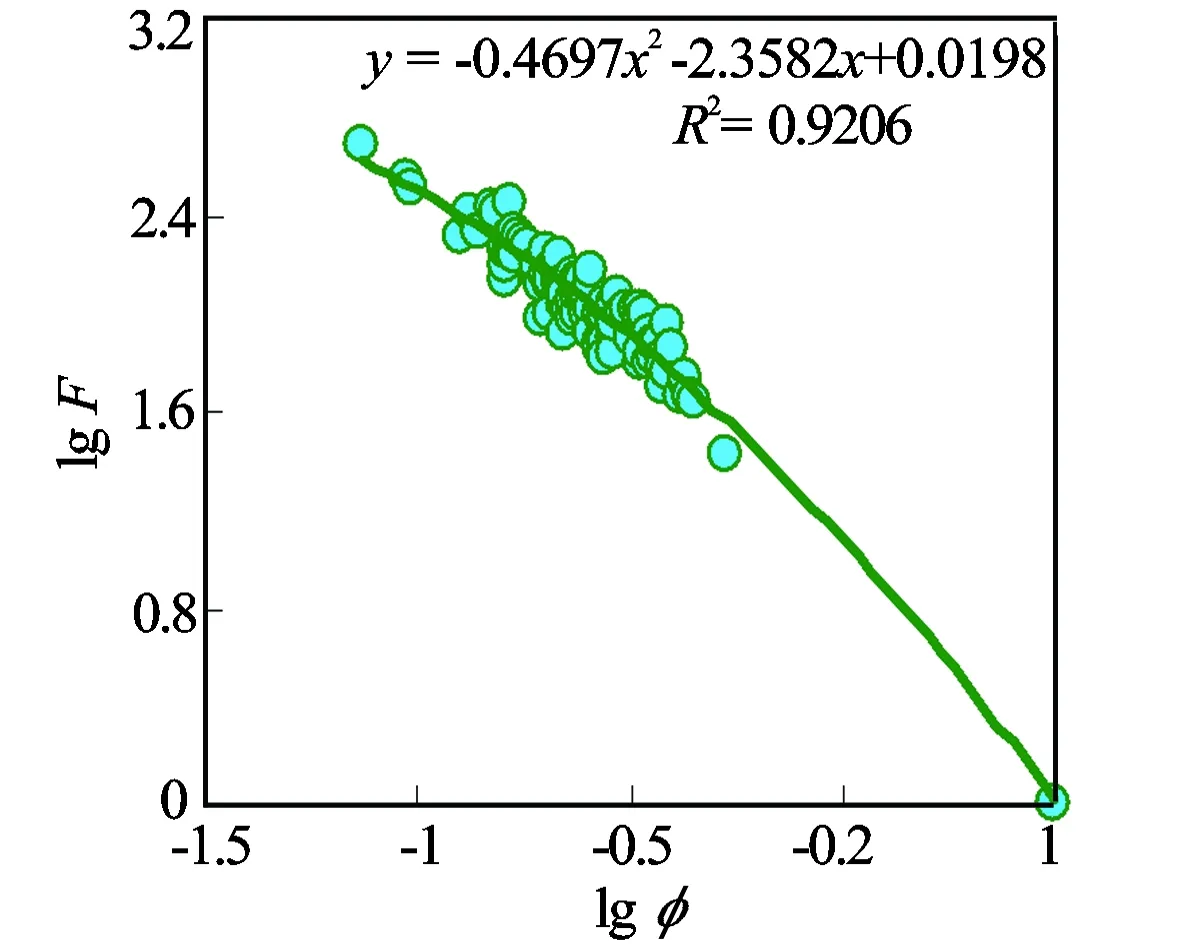
图3 苏里格气田盒8段和山1段岩样地层因素对数与孔隙度对数关系图

R2=0.9206

(1)

2.2 岩电参数b优化方法

相关文献表明,系数b是一个与岩性有关的参数[9]。基于此,采用主成分方法从能够反映岩性变化的测井参数(自然伽马、光电吸收截面指数、中子—密度孔隙度差异[10])中提取综合主成分Z。可以看出,系数b并不像经典理论值那样总等于1,而是随着岩性综合主成分的增大呈现出先减小后增大的变化规律。b值变化规律的非单调性表明岩性变化造成了导电特性的复杂性(见图4)。

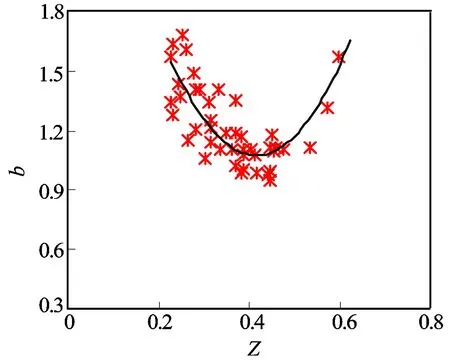
图4 岩电参数b与岩性综合主成分Z关系图

2.3 岩电参数n优化方法

图5为电阻率增大指数随含水饱和度的3种变化规律图。对所有样本采用幂函数回归得到的岩电参数n是根据总样本的平均响应值。对此次岩电实验资料数据,实际存在3种电阻率增大指数随含水饱和度的变化规律。根据3组样本可得

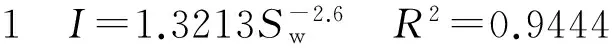
(2)

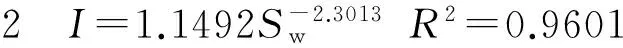
(3)

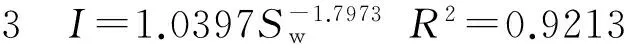
(4)

根据式(2)至式(4)可知,模型1至模型3相应样本的平均岩性系数b值依次减小,分别为1.321 3、1.149 2和1.039 7;同样,平均饱和度指数n也表现为相同的递减趋势,分别为2.6、2.301 3和1.797 3。显然,采用单一的岩电参数b值和n值计算饱和度,其结果难免存在较大的误差。

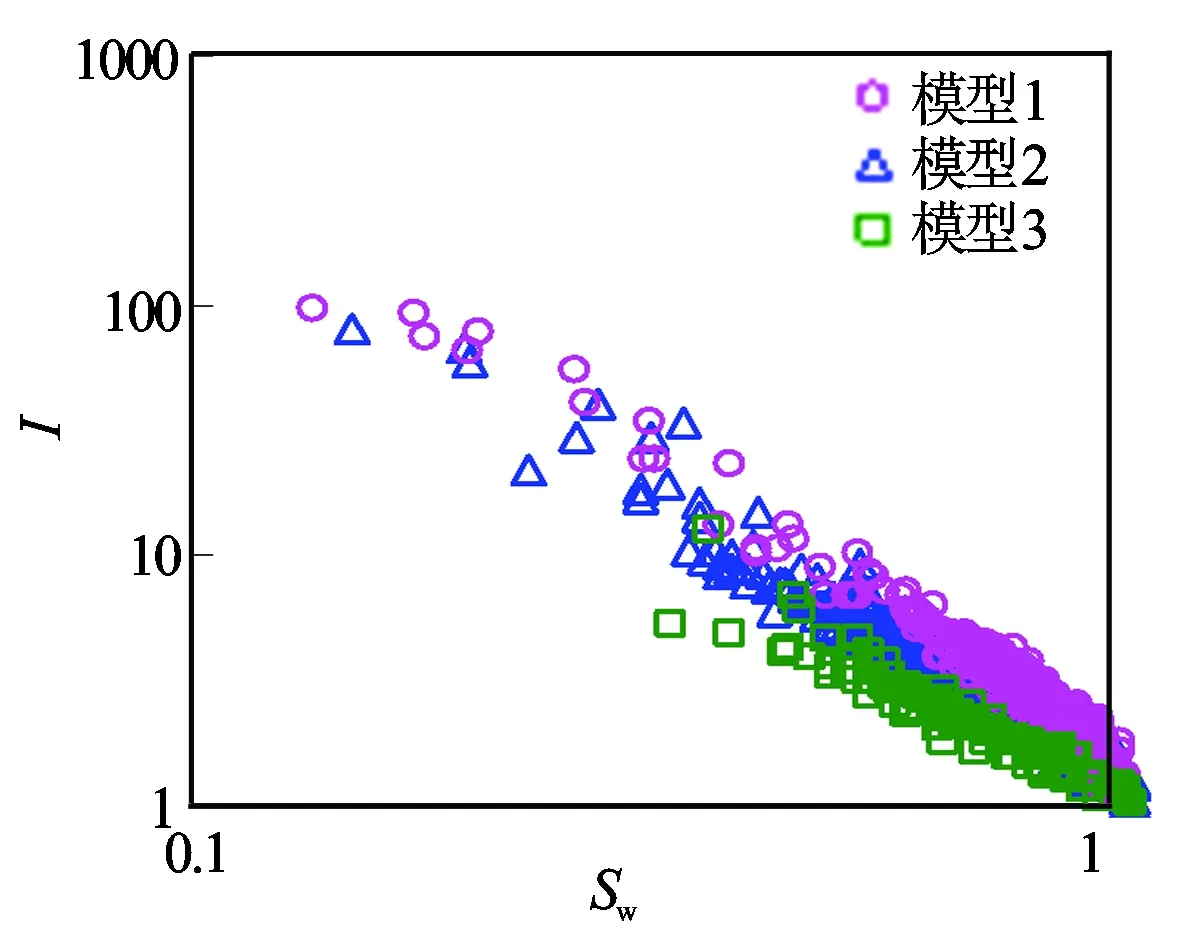
图5 电阻率增大指数随含水饱和度的3种变化规律

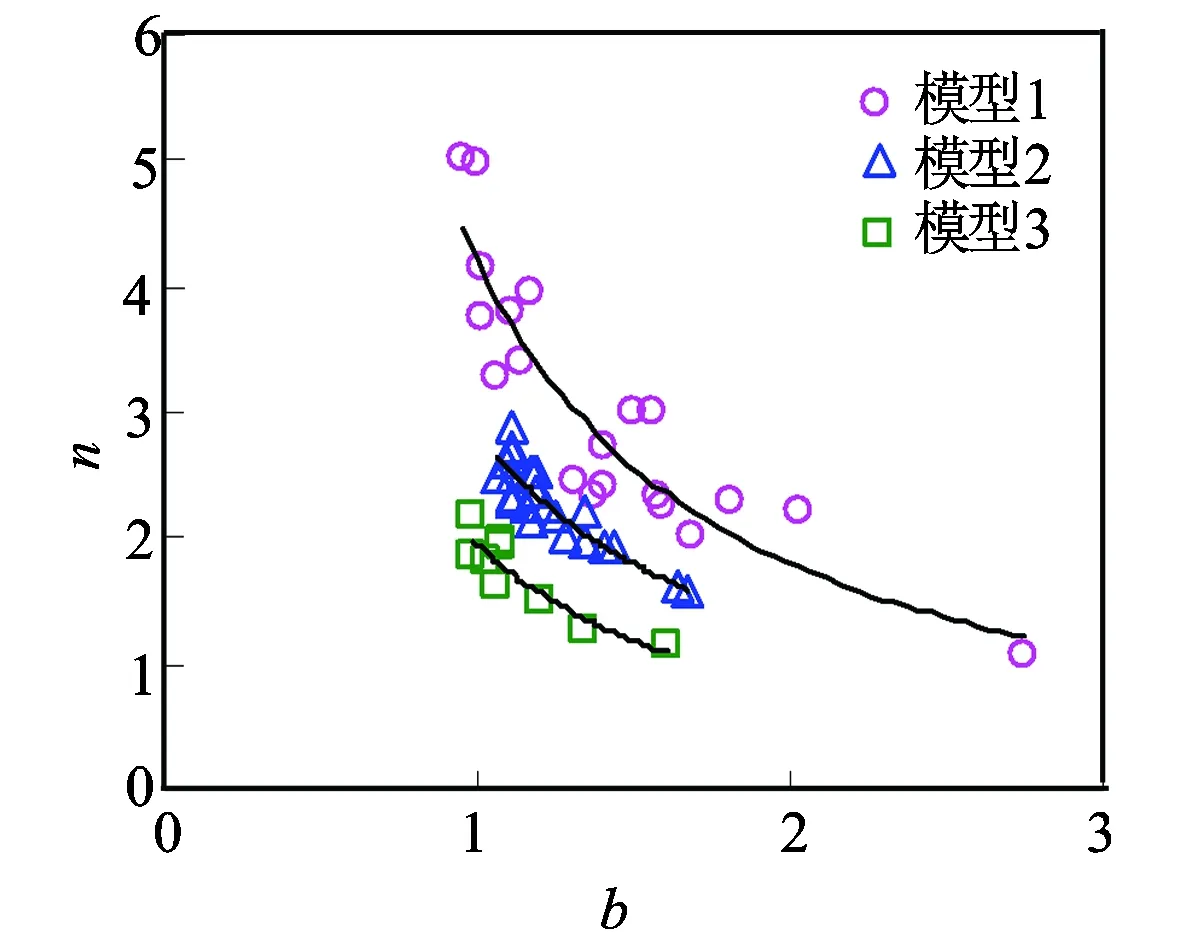
图6 3种电阻率增大指数随饱和度变化规律样本的b值与n值关系图

图6为3种电阻率增大指数随饱和度变化规律样本的b值与n值关系图。对比图5、图6可知,所有样本系数b值和饱和度指数n值之间并没有明显的相关性,但对于每种变化规律所包括的样本而言(见图6),其系数b值与饱和度指数n值之间均存在较好的幂函数关系。3种变化规律可表示为

模型1n=4.1951b-1.2229R2=0.8524

(5)

模型2n=2.8353b-1.1238R2=0.8265

(6)

模型3n=1.955b-1.2407R2=0.8564

(7)

因此,只要区分出3类变化规律所对应储层的测井响应特征,就可以在计算出系数b值的基础上,通过式(5)至式(7)得到连续变化的饱和度指数n值。

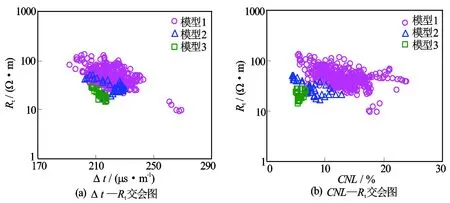
图7 饱和度指数n值模型分类图版

饱和度指数n值模型选择步骤:①通过式(1)得到b值并分别带入式(5)至式(7),将计算的3组n值分别代入阿尔奇公式,根据饱和度计算值与密闭取心井的岩心分析值的误差分析,确定处理层段所采用的n值模型;②提取不同n值模型对应的地层测井响应值,通过交会图分析,确定n值模型分类图版。基于上述思路,应用4口密闭取心井的576个岩样测井数据,通过不同n值模型对应地层的测井响应特征的对比分析,建立了饱和度n值模型分类图版(见图7)。 分析可知,在相同的孔隙度测井响应条件下,从模型1到模型3样本的电阻率响应整体上表现为逐渐减小的趋势,显示了3类储层气水分布状态的差异。对于非均质储层而言,含水饱和度指数n值主要与导电部分的孔隙结构分布有关,即与岩石的电曲折度有关。电曲折度越大,导电部分孔隙结构越复杂,相应的含水饱和度指数n值就越低,这与图5揭示的3类模型平均饱和度指数逐渐减小的结论相符合。

根据饱和度指数n值模型的分类图版,结合式(5)至式(7)即可得到连续变化的饱和度指数。

3 应用效果

应用本文方法对实际井资料进行处理,采用固定岩电参数和变岩电参数计算的饱和度与岩心分析饱和度效果对比(见图8)。根据水分析化验资料可知,地层水电阻率约为0.06 Ω·m[11]。图8为苏××井(密闭取心井)饱和度优化处理效果对比图。根据饱和度指数n值分类图版,图8中解释层段从上到下饱和度n值计算模型分别选择模型1、模型2和模型3,表明随气水分布状态的变化,n值表现出较大的差异性。采用固定统一岩电参数计算饱和度时,下部储层计算值明显小于岩心分析值,应用本文的变岩电参数方法得到饱和度计算值更能反映地层含气饱和度真实情况,计算精度有了较明显的提高。

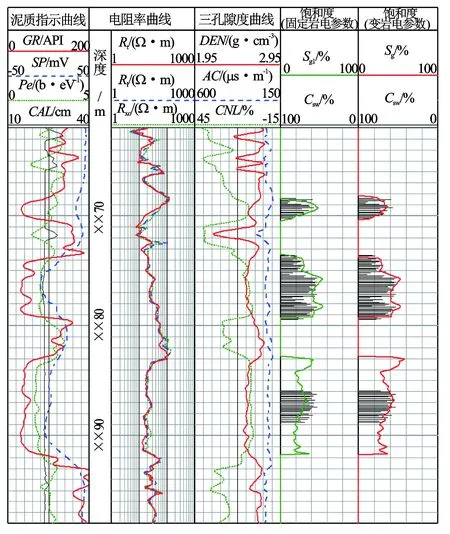
图8 苏××井饱和度处理效果对比图

含水饱和度平均含水饱和度/%平均绝对误差/%平均相对误差/%岩心分析65.02——Sw(变岩电参数)63.351.672.57Sw1(固定岩电参数)53.9511.0717.03

表1为苏里格气田密闭取心井饱和度计算误差对比表。根据4口密闭取心井576个样本实际处理结果,采用固定岩电参数计算的饱和度与岩心分析结果相差较大,平均绝对误差和平均相对误差依次为11.07%和17.03%;应用变岩电参数得到的饱和度计算值与密闭取心井岩心分析饱和度吻合较好,计算值平均绝对误差和平均相对误差依次为1.67%和2.57%,计算精度比优化前有较明显的提高,平均绝对误差和平均相对误差分别提高9.4%和14.46%。

4 结 论

(1) 对于低孔隙度低渗透率储层其岩石导电特性异常复杂,根据岩电实验得到的岩电参数与经典理论值相差较大,固定的岩电参数只是岩石样本特征的平均响应值,难以反映不同储层类型的导电特性,为饱和度的精细解释造成较大的困扰。

(2) 利用本文提出的岩电参数优化方法能够连续计算地层变化的岩电参数。通过苏里格气田低孔隙度低渗透率气层的实际资料处理,证实该方法较采用固定岩电参数得到的饱和度计算值精度更高,计算结果与岩心分析结果之间吻合更好,能真实反映低孔隙度低渗透率气层的饱和度。

参考文献:

[1] 孙小平, 石玉江, 姜英昆. 复杂孔隙结构储层含气饱和度评价方法 [J]. 天然气工业, 2000, 20(3): 41-44.

[2] Archie G E. The Electrical Resistivity Log as Aid in Determining Some Reservoir Characteristics [J]. Trans AIME, 1942, 146: 54-62.

[3] 曾文冲. 油气藏储集层测井评价技术 [M]. 北京: 石油工业出版社, 1991: 92-134.

[4] 王黎, 孙宝佃, 沈爱新, 等. 某油田低孔隙度低渗透率泥质砂岩储层岩电实验及应用 [J]. 测井技术, 2005, 29(2): 91-94.

[5] Edmondson H N. Archie’s Law: Electrical Conduction in Clear, Water-bearing Rock [J]. The Technical Review, 1988, 36(3): 4-13.

[6] Edmondson H N. Archie’s Law: Electrical Conduction in Hydrocarbon-bearing Rock [J]. The Technical Review, 1988, 36(4): 12-21.

[7] Jin G, Terres-Verdin C, Devarajan S, et al. Pore-scale Analysis of the Waxman-Smits Shaly Sand Conductivity Model [J]. Petrophysics, 2007, 48(1): 104-120.

[8] David K. The Porosity-Resisitivity-Saturation Relationship——An Alternative to Archie’s Model [J]. Petrophysics, 2007, 48(5): 335-361

[9] 孙建国. 阿尔奇(Archie)公式: 提出背景与早期争论 [J]. 地球物理学进展, 2007, 22(2): 472-486.

[10] Gaymard G, Poupon A. Response of Neutron and Formation Density Logs in Hydrocarbon Bearing Formations [J]. The Log Analyst, 1968, 9(5): 3-12.

[11] 张海涛. 苏里格地区有效储层测井识别方法研究 [D]. 西安: 西北大学, 2010.