测录井结合神经网络流体识别技术在高邮凹陷阜宁组的应用

任培罡, 尹军强, 杨加太, 曹书坡, 雷磊

(1.中国石化江苏石油工程有限公司地质测井处, 江苏 扬州 225007;2.江苏油田博士后工作站, 江苏 扬州 225007)

0 引 言

江苏油田高邮凹陷阜宁组低孔隙度低渗透率油气层测井响应受岩性、物性和地层水影响较大,测井识别油气的信噪比降低,不同流体储层的电阻率差异变小,流体识别困难。虽然录井资料获得的是地下油气的直接信息,具有直观准确的特点,受油气藏储层岩性、地层水性质、物性影响相对较小,但其缺点是采样间隔大、分层精度低、储层厚度解释不够精确。基于以上认识,提出了综合测井与录井,发挥测井和录井资料的各自优势,对低孔隙度低渗透率储层开展油气识别,并将人工智能中较为成熟的BP神经网络技术应用到油气解释中,提出了一种基于BP人工神经网络的综合测、录井资料对低孔隙度低渗透率储层进行油气识别的新方法,在江苏油田高邮凹陷阜宁组低孔隙度低渗透率储层流体解释中应用,取得了较好的效果。

1 BP神经网络算法的改进

在实际应用中最基本的BP神经网络算法存在许多不足,普遍公认的问题是收敛速度慢和容易陷入局部极小。另外,隐层神经元个数的确定存在盲目性[1]。本文方法改进了BP神经网络算法的不足。

(1) 加入动量项,提高收敛速度和避免陷入局部极小。BP算法中学习步长η的选取很重要,η值大,网络收敛快,但过大会引起振荡不稳定;η值过小,收敛速度变慢。要解决这一矛盾最简单的方法是加入动量项,即令

Δωij(n+1)=αΔωij(n)+ηδj(n)οj

(1)

式中,α为动量项,通常为整数;n+1表示第n+1次迭代;第2项表示ωij第n+1次修正量应该在一定程度上保持第n次修正量的惯性,使变化律的惯量在某种程度上守恒。在BP算法中加入动量项不仅可以微调连接权值的修正量,加快收敛速度,也可以使学习避免陷入局部极小[2-4]。

(2) 自适应调整学习参数η。BP算法学习过程的长短与每次迭代的步长(学习率)η有很大的关系。最优学习步长的选取与局部误差的曲面形状有关,由此根据2次迭代结果的误差变化和误差的变化趋势建立η调整规则,确定一个对当前状态较好的学习步长。

每个迭代步骤考察所有样本的误差平方和较上次迭代是否有所下降,再对学习率加以调整。每个迭代步骤考察样本输出和实际输出的误差平方。

(2)

在迭代开始时,采用较小的学习率,每迭代一次考察总误差是否下降,学习率的选取

η(t+1)=βη(t)

(3)

如果E(t)1;反之则0<β<1。

这种方法使网络在学习时能够自适应地根据误差曲面的要求调整连接权值,使网络避免在学习过程中陷入局部极小和发生振荡现象,大大加速网络的收敛速度。

(3) 优化网络结构,确定隐层神经元个数。BP算法的学习其层节点个数的选取成为决定网络性能的关键。实际应用中一般根据经验和实验结果选取适当的隐节点数。雷鸣等提出了自构神经网络算法,其思想是先用较多的隐层神经元确定初始神经网络模型,然后根据隐层神经元之间的相关性使其在学习中将冗余的隐层神经元合并或删除,从而构造出合适的网络拓扑结构,这种网络称为自构形快速BP网络。隐层神经元之间的相关性用相关系数和样本分散度评价[5]。

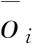
(4)

它们之间的相关系数为

(5)

隐层神经元的相关系数说明同一隐层神经元间的输出线性相关。当Rij较大时,说明其中有冗余单元,需要压缩。

样本分散度定义为

(6)

样本分散度说明隐层神经元i输出与平均输出之间的差异情况。样本分散度过小,说明该神经元没有起作用,需要删除[6-10]。隐层冗余神经元合并和删除原则:

(1) 神经元合并原则。同一隐层中相关系数过高的2个神经元在满足下述条件时给与合并[11-14],即

|Rij|≥σ1,且Qi、Qj≥σ2

(7)

式中,σ1、σ2为规定的门限值。其中σ1为相关系数的上限值,一般取为0.6～0.9;σ2为分散度的下限值,一般取为0.001～0.01。2个神经元i、j合并为一个神经元i,其与后一层任一神经元k的连接权值和阈值修正

wk i←wk i+awk j

(8)

θk←θk+bwk j

(9)

其中

(10)

(2) 无效神经元删除原则。当样本的分散度Qi<σ2时,该隐层神经元可以删除。删除后其后一层任一神经元k的阈值调整

θk←θk+oi·wk i

(11)

2 测录井资料结合建立神经网络

2.1 学习样本参数的选取

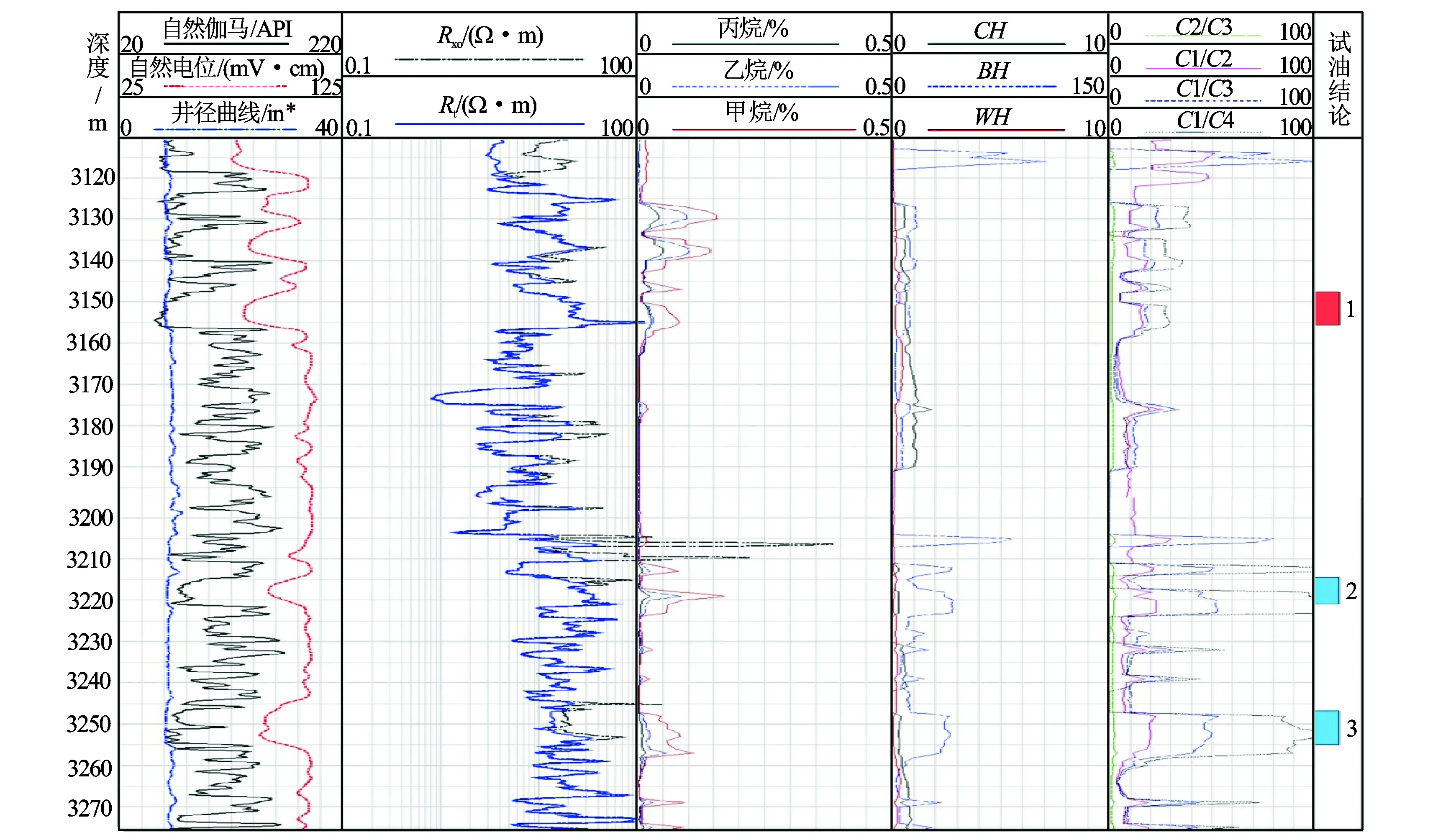
图1 曲线敏感性分析图

(1) 参数敏感性分析。通过对常规曲线和气测曲线值的综合响应分析(见图1),地层真电阻率Rt、孔隙度指示曲线AC以及泥质指示曲线GR对储层响应强烈。气测录井资料中绝对含量3组参数、相对含量4组比值以及气测录井油气性质识别的派生参数3组对油气层识别较为敏感。

(2) 输入参数的选取。选取对流体性质识别贡献较大的测井和气测录井资料作为神经网络输入。

测井资料选取的参数:选取声波曲线(AC)和深电阻率曲线(Rt)以及自然伽马曲线(GR)等3个参数作为测井输入;从14个气测录井资料中挑选出气测录井资料的绝对含量,分别为甲烷(C1)、乙烷(C2)、丙烷(C3)以及相对含量C1/C2、C1/C3、C1/C4、C2/C3和气测录井油气性质识别的派生参数烃湿度比(WH)、烃平衡比(BH)、烃特征比(CH)等10个参数作为录井资料输入信息。上述派生参数来源于气测录井识别油水方法涉及的3个参数,其计算公式如下。

*非法定计量单位,1 ft=12 in=0.304 8 m,下同

烃湿度比

WH=(C2+C3+C4+C5)/(C1+C2+

C3+C4)

(12)

烃平衡比

BH=(C1+C2)/(C3+C4+C5)

(13)

烃特征比

CH=(C4+C5)/C3

(14)

共选取以上13个参数作为网络的输入,即网络输入层神经元个数为13。

(3) 输出参数的确定与编码。根据试油资料的储层类型和常规方法的解释结论,并结合输入参数对各种储层流体性质的敏感程度。最终确定输出层的储层分类类型为油层、水层、干层3个类型,分别对应输出层的3个神经元。为了实现神经网络的计算机数字化处理,分别对3种储层分类类型编码:油层(0.9,0.1,0.1)、水层(0.1,0.9,0.1)、干层(0.1,0.1,0.9)。

神经元的激励函数采用Sigmoid形函数,其渐进值为1和0(见图2)。其取值很难达到0和1,为了避免学习算法不收敛,提高学习速度,对输出参数的编码为0.1和0.9,而不取1和0。

图2 Sigmoid函数图

2.2 学习样本的选取与预处理

首先用统计方法对各种参数进行深度对齐和环境校正,以避免井眼环境、钻井条件、仪器误差和人为操作对测井和录井资料准确性造成的影响。在深度对齐处理中以测井深度为准。为了能达到2类参数应用不存在深度误差,一般将气测地质录井资料按测井资料的采样间隔进行采样并加入wis文件进行处理。

以试油资料的储层流体类型为准,对校正后的资料在储层厚度内读取各学习参数平均值,获得和已建立的BP神经网络模型中3种储层流体类型相对应的学习样本。由于测井资料和气测录井资料组成的学习样本数值在数量级上有很大的不同,如测井参数AC的数值范围在130～30 μs/ft之间,而气测录井参数QT等参数的数值范围却仅仅在1～10之间。如果这些数据直接加入网络模型中进行学习预测,致使网络学习的计算量增大、学习速度变慢并且预测精度也会大大下降,因此,必须对样本数据进行归一化处理。采用的归一化方法

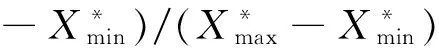
(15)

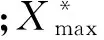
各输入参数经过归一化处理后其数值均被统一在(0,1)之间,这样形成的样本集进行BP网络学习可以减小学习的计算量,放大了不同储层类型所对应的样本参数间的差距,提高了流体类型预测精度。

将地层的层响应特征值作为油气水识别网络的输入信息,能更好地进行层段油水识别。以试油资料的储层流体类型为准,对校正后的资料在储层厚度内读取各学习参数平均值,获得和已建立的BP神经网络模型中3种储层类型相对应的学习样本,对样本进行逐一筛选,从中剔除矛盾样本,适当减少相同特征点数,补充特征明显的典型样点,以保证样本具有真实性、代表性和广泛性。应用以上方法,在苏北盆地经过几次挑选及验证,最终共获得3种储层类型的26个样本组成学习样本集(见表1)。

2.3 网络结构的确定

在输入和输出确定的同时,分别进行了1层隐含层和2层隐含层的学习预测,并对比分析油水识别效果发现,1层隐含层即3层网络结构预测结果较2层隐含层预测效果更好、更稳定,由此最终确定用3层网络结构。隐含层神经元的个数应用网络结构优化的自构形算法在学习过程中自动确定,最终确定为11个。

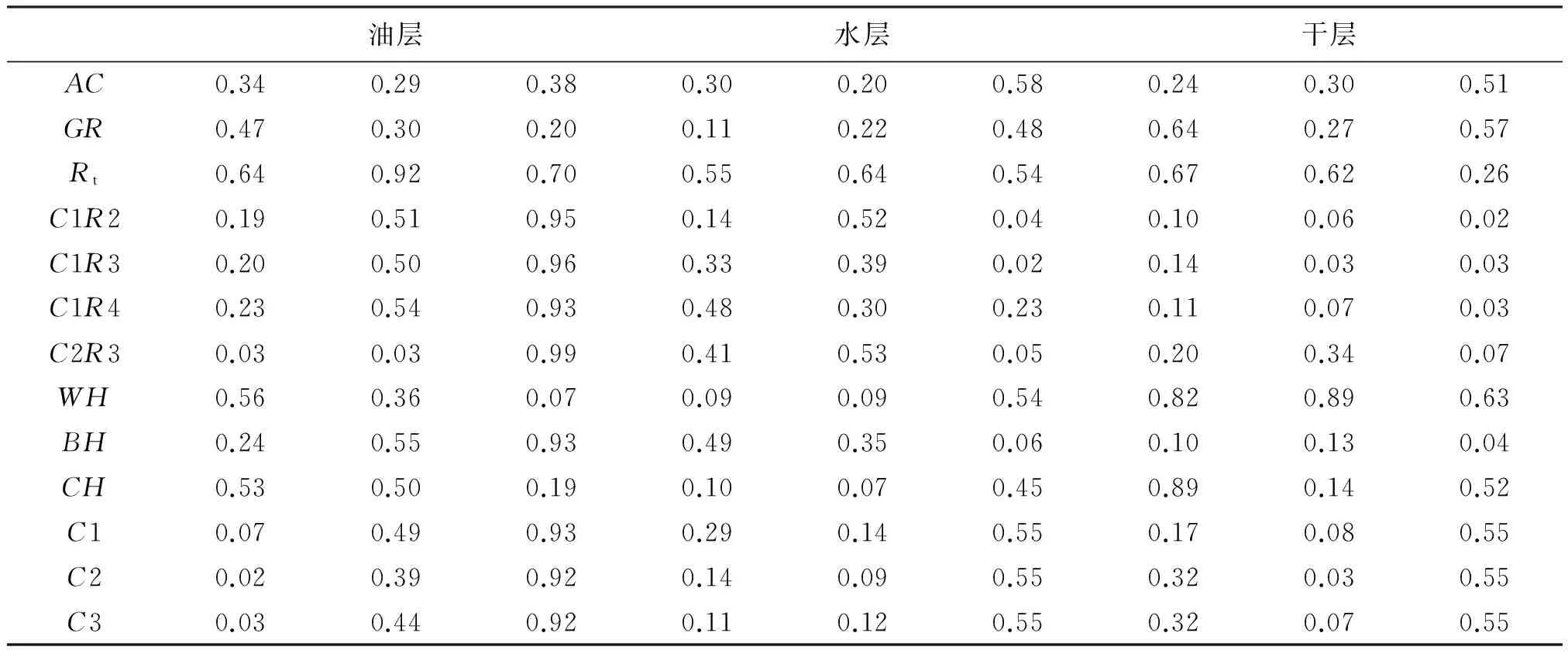
表1 苏北盆地归一化学习样本表

学习样本的数量不是一次就确定合适,而是一个由最基本样本数开始经过学习和预测再添加样本,再学习和预测多次循环往复的过程,每次循环均比上次效果有所提高,呈螺旋上升过程。研究首先选取了26个样本与3种储层类型组成学习样本集,通过学习预测,预测效果不满足要求,再经过挑选并添加,确定了最终学习样本集。

最终建立测录井综合资料储层解释神经网络结构为输入层神经元13个,隐含层为1层,11个神经元,输出层神经元3个,并保存了连接权值及阈值以实现储层外推预测。

3 实例分析

应用改进后的神经网络对江苏油田×1井储层进行了实际应用,油气层预测结论与试油结论基本一致。图3为江苏油田×1井神经网络预测结果图与原解释成果图的对比。井段2 976～2 980 m试油结论为油层,原测井解释结论为油层。应用修改后的BP神经网络法进行解释,第4道和第5道分别是油层和水层的预测成果曲线,计算油层线约为0.9,水层线小于0.3,解释储层为油层,与试油结果一致。井段3 437～3 448 m试油结论为水层,而原测井解释结论为油层,与试油结论不符。应用修改后的BP神经网络法进行解释,在第4道中计算的油层线在0.2左右,第5道中计算水层线约为0.9,解释为水层,与试油结论吻合。

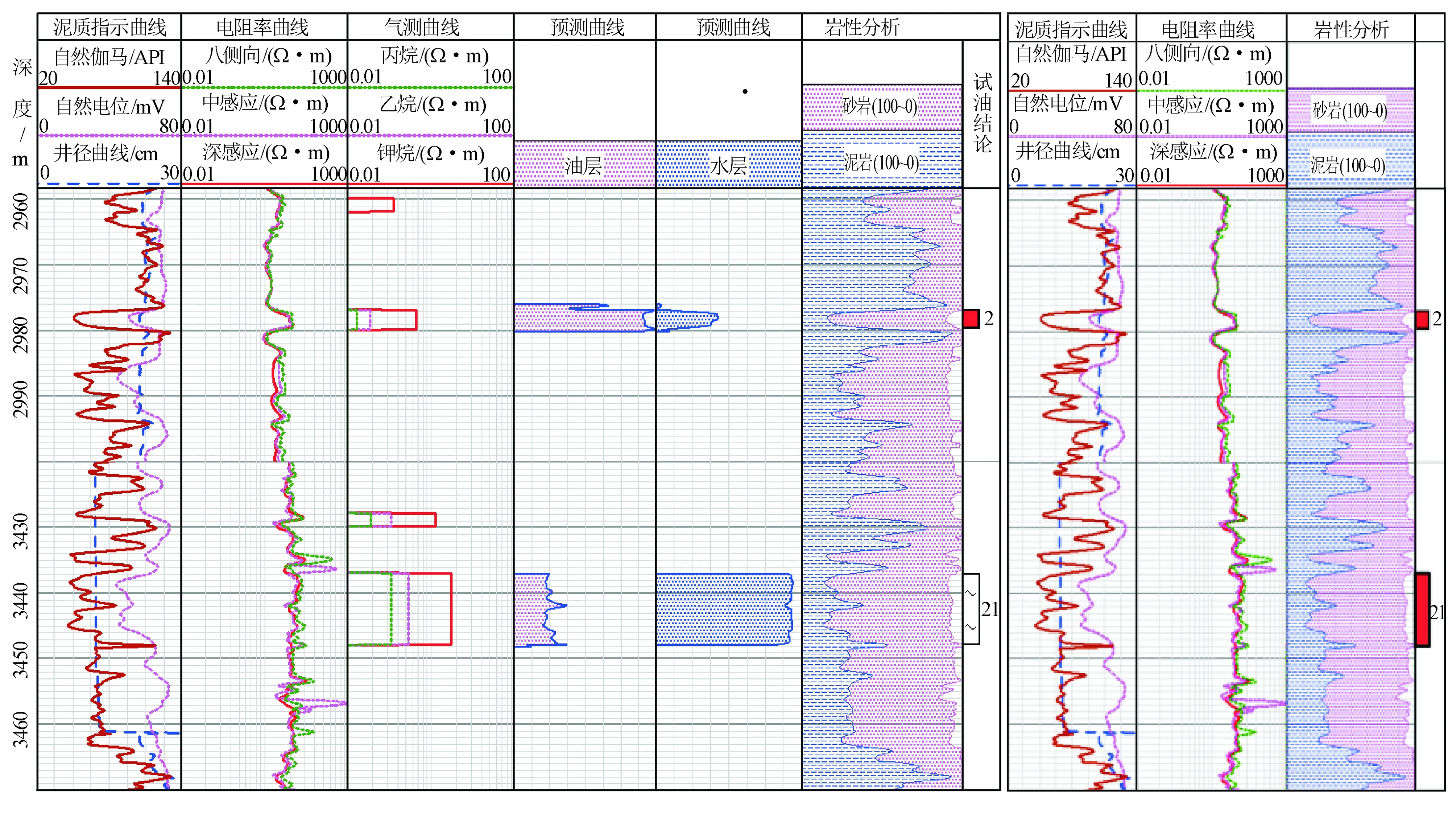
图3 ×1井神经网络预测结果图与原解释成果图

应用修改后的BP算法将测录井资料综合应用之后,解释处理新井60多口,单层解释符合率达到85%以上,对低孔隙度低渗透率流体性质的识别能力大大提高,提高了解释符合率。

4 结 论

(1) 改进后的BP算法通过加入动量项提高收敛速度且避免陷入局部极小,自适应调整学习参数,优化网络结构,确定隐层神经元个数;同时将测井资料、录井资料相结合,有效提高了高邮凹陷低孔隙度低渗透率储层流体识别的准确性。

(2) 该方法在测井资料与录井资料具有较好相关性的地区应用效果较好,但是在构造复杂、储层变化快、测井质量差的地区应用效果较差,应结合不同地区实际情况,进行更为深入研究。

参考文献:

[1] 刘瑞林. 神经网络在油气评价和预测方面的应用研究 [J]. 地球物理学进展, 1995, 10(2): 20-241.

[2] 杨小明. 神经网络模型识别碳酸盐岩储层方法研究 [D].荆州: 长江大学, 2005.[3] 罗利,姚声贤.神经网络及模式识别技术在测井解释中的应用[J].测井技术,2002,26(5):364-368.

[4] 侯俊胜, 尉中良. 自组织神经网络在测井资料解释中的应用 [J]. 测井技术, 1996, 20(3): 197-200.

[5] 雷鸣, 楚威, 李阳. 基于BP神经网络的系统综合效能评估方法 [J]. 指挥系统与技术, 2012, 3(1): 8-19.

[6] 王向公. 应用地球物理常用数学方法 [M]. 武汉: 武汉工业大学出版社, 1995.

[7] 薛林福, 潘保芝. 自组织神经网络自动识别岩相 [J]. 长春科技大学学报, 1999, 29(2): 144-147.

[8] 张治国, 杨毅恒, 夏立显. 自组织特征映射神经网络在测井岩性识别中的应用 [J]. 地球物理学进展, 2005, 20(2): 332-336.

[9] 许少华, 刘扬, 何新贵. 基于过程神经网络的水淹层自动识别系统 [J]. 石油学报, 2004, 25(4): 54-57.

[10] 阎铁, 刘春天, 毕雪亮, 等. 人工神经网络在大庆深井钻头优选中的应用 [J]. 石油学报, 2002, 23(4): 102-106.

[11] Burns B A. Fluvial Responesin Asequence Stratigraphic Framework: Example from the Montserrat Fan Delta, Spain [J]. Joural of Sedimentary Research, 1997, 67(2): 311-321.

[12] 李道伦, 卢德唐, 孔祥言. 基于径向基函数的隐式曲线 [J]. 计算机研究与发展, 2005, 42(4): 599-603.

[13] Li Daolun, Lu Detang, Kong Xiangyan. Implicit Curves and Surfaces Based on BP Neural Network [J]. Journal of Information & Computational Science, 2005, 2(2): 259-271.

[14] Rolon L F, Mohagegh S D, Ameri S, et al. Developing Synthetic Well Logs for the Upper Devonian Units in Southern Pennsylvania [C]∥SPE98013, 2005: 1-10.