薄层电阻率的测井响应校正方法研究
王欣,潘雨舟
(中国石化华东分公司石油勘探开发研究院,江苏南京210011)
薄层电阻率的测井响应校正方法研究
王欣,潘雨舟
(中国石化华东分公司石油勘探开发研究院,江苏南京210011)
厚度小于2 m的储层,由于受仪器纵向分辨率的限制,其电阻率的测井响应受围岩影响较大,往往很难直接反映目标地层的真实电阻率值。通过有限元数值模拟的方法,模拟了不同厚度下(0.1~10 m)的电测井响应值,取地层真实电阻率与其比值来确定储层电阻率的校正系数,在此基础上,编制了不同厚度下电测井响应的校正图版。苏北G区块的实例证明,应用校正图版校正后的薄层电阻率值更接近真实地层电阻率。
薄层;电测井响应;有限元
电测井仪器结构复杂,即便对最简单的地层模型,其响应也没有解析解,只能采用数值的方法来模拟实际的仪器响应。在电测井尤其是侧向测井领域,有限元法是使用最早最成熟的数值模拟手段。1971年,Coggon首次将有限元方法引入电测井[1]。张庚骥(1986年)引入波前法后又大大提高了有限元法在电阻率测井响应数值模拟中的计算效率[2]。随后的刘振华(2002年)、范宜仁(2009年)、王欣(2012年)、仵杰(2013年)等利用数值模拟的方法在研究厚度变化对电测井响应影响方面做了大量工作[3-6]。
本文基于前人研究,结合苏北地区油田储层实际,利用有限元法对不同厚度储层的电测井响应进行数值模拟,编制了适合苏北地区不同厚度电测井响应的校正图版。利用该图版可以为测井解释人员正确认识储层电阻率,尤其是正确认识薄层电阻率提供参考,为油水层的准确识别提供基础。
1 电测井响应有限元模型
首先是建立有限元模拟电测井响应的数学模型。为简化分析,以具有轴对称情形的直井侧向测井为例。直井模型下侧向测井响应的定解问题可以归结为:求出一个连续而且适当光滑的函数U,它满足以下各条件:在求解域Ω内满足方程:
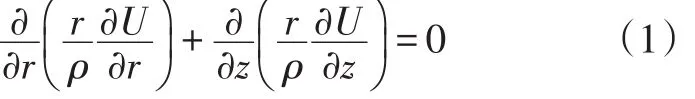
这里采用柱坐标形式,式中U是电位,ρ是介质的电阻率。在各个电极的表面满足方程:
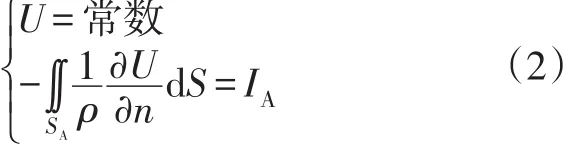
式中:n是边界面的法线向量,SA是电极A的表面积,IA是电极发射或接收的电流强度。在绝缘边界满足第二类边界条件:

在无穷远边界满足第一类边界条件:

以上是直井模型下定解问题中函数U所应满足的全部条件。直井模型的泛函极值形式可以表述为:在求解域Ω中求解这样一个函数U,它使得泛函F(U)取极值(最小值)。其中:
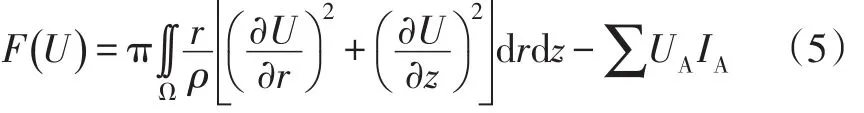
式中:UA和IA为电极的电位和电流。结合侧向测井需要满足的约束条件,可以根据式(6)计算出目标地层的电测井响应视电阻率值Ra。

式中:K为仪器常数,UM为监督电极的电位,I0为主电极的电流。
2 泥浆侵入的数值模拟
鉴于ECLIPS-5700系列双侧向测井仪在苏北地区应用较为广泛,本文用有限元方法模拟该仪器深电阻率响应。表1给出了不同储层厚度下(28个采样点)的电测井响应值。苏北油田储层电阻率主要分布范围为0.2~20 Ω·m,围岩电阻率在1 Ω·m左右,本文进行数值模拟时围岩电阻率取1 Ω·m,储层电阻率取3 Ω·m,不考虑井径和泥浆侵入等因素影响。校正系数定义为储层电阻率与测井响应值的比值。
图1给出了不同层厚下地层电阻率值的校正图版,可以看出,2 m以上的储层校正系数接近于1,基本可以不用校正。2 m以下的储层随着厚度的减小校正系数急剧增大,测井响应值已经远远小于地层的真实电阻率值,如果不加以校正,解释人员很容易对储层产生错误的判别。
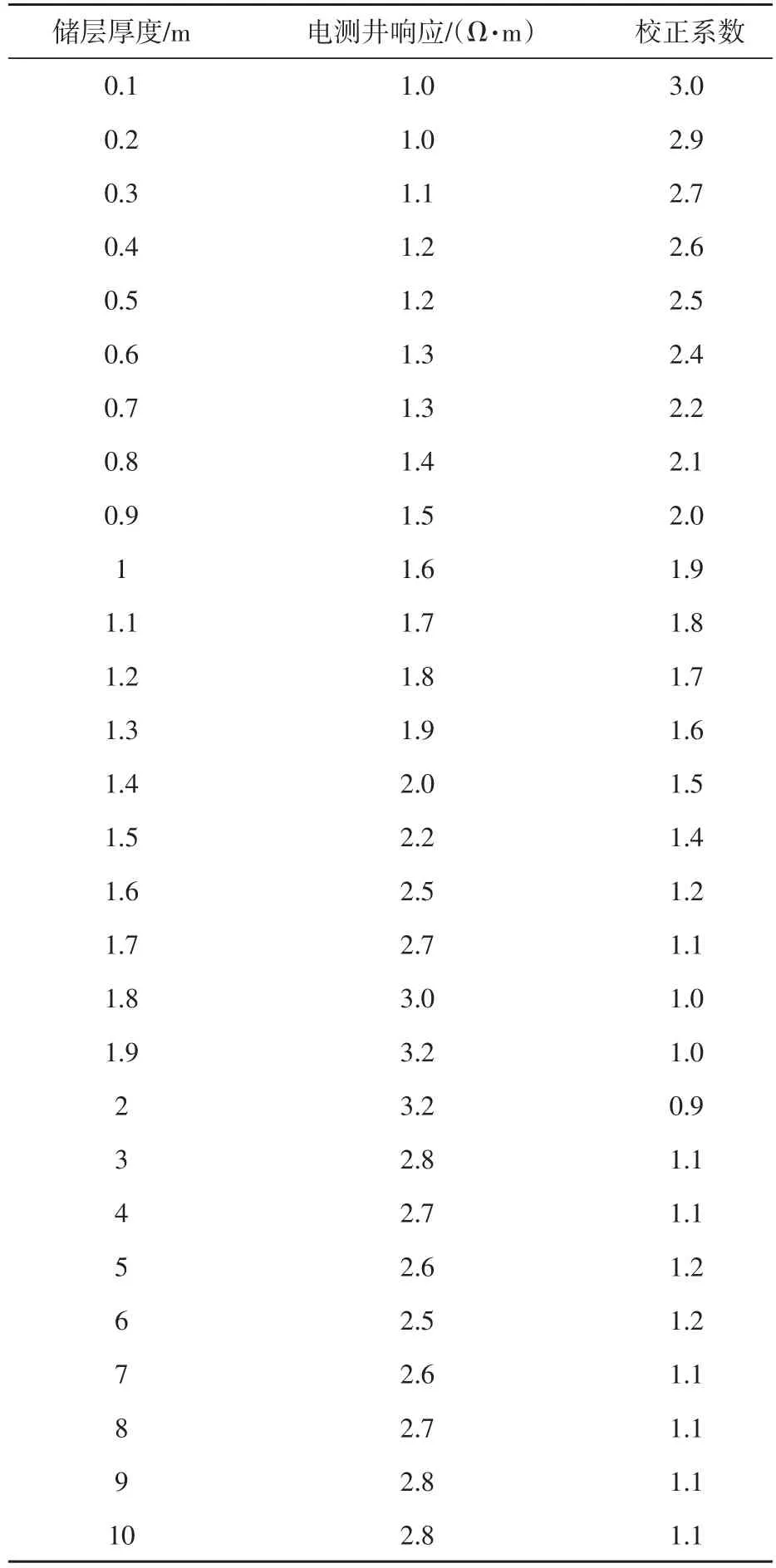
表1 不同储层厚度下校正系数Table 1 CF of different reservoir thickness
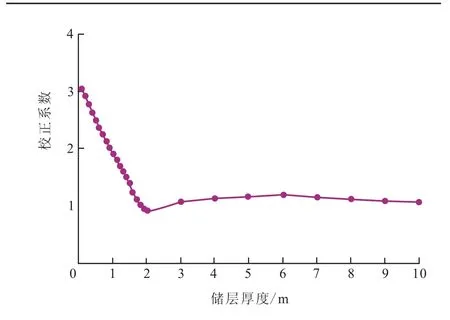
图1 不同层厚下地层电阻率值校正图版Fig.1 Formation resistivity correction chart of different reservoir thickness

表2 储层电阻率值校正前后对比Table 2 Comparison of reservoir resistivity before and after correction
为了验证校正图版的适用性,本文给出了苏北G区块的应用实例。图2是G-1井的测井响应曲线图。
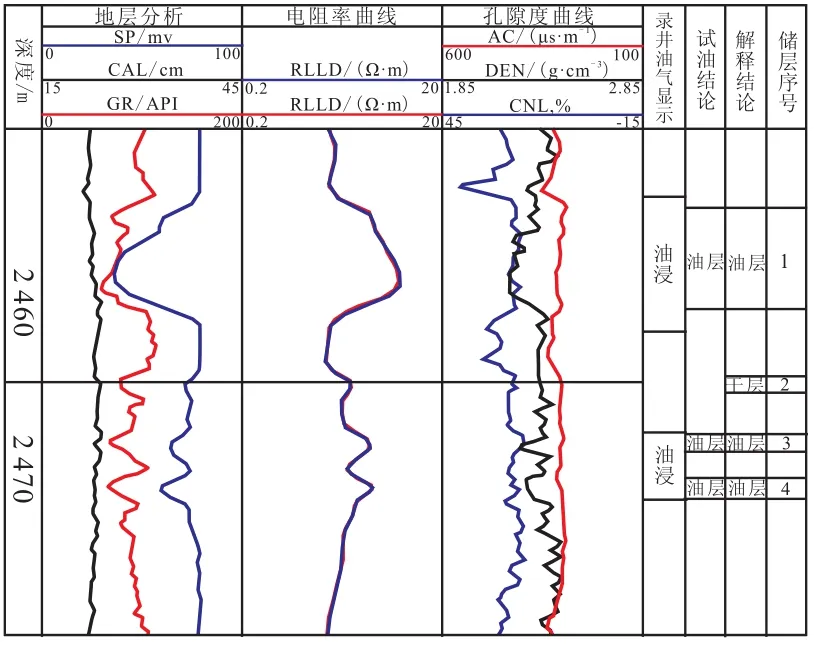
图2 苏北G区块G-1井测井响应曲线Fig.2 Log response curves of well G-1 in block G, North Jiangsu oilfield
G区块油层的电阻率下限值为4.5 Ω·m,孔隙度下限值为18%。如果不进行电阻率的校正,3、4号储层易被划分为水层或含油水层。这与试油结论不相符合,G-1井1、3、4层录井显示为油浸,三层合试日产油11.51 t,日产水0.33 t,试油结论为油层。
表2给出了G-1井1、3、4号储层电阻率的测井响应值和校正后值的对比情况。可以看出,经过校正图版校正后的3、4号储层电阻率值与1号储层比较接近,在油层下限值之上。说明校正后的电阻率值更能反映地层的真实电阻率。
3 结论
1)厚度小于2 m的储层电阻率测井响应值一般要小于地层真实电阻率值,随着储层厚度的减小,测井响应值与地层真实电阻率值间的差距急剧增加。
2)经过图版校正后的薄层电阻率值更能反映地层的真实电阻率,能为测井解释中储层的划分提供更为准确的依据。
[1]Coggon J H.Electromagnetic and electrical modeling by the fi⁃nite element method[J].Geophysics,1971,36(1):132-155.
[2]张庚骥.电法测井(下)[M].北京:石油工业出版社,1986.
[3]刘振华,胡启.阵列侧向测井响应的计算及其特征[J].西安石油学院学报(自然科学版),2002,17(1):53-57.
[4]范宜仁,蒋建亮,邓少贵,等.高分辨率阵列侧向测井响应数值模拟[J].测井技术,2009,33(4):333-336.
[5]王欣,陈浩,王秀明,等.双侧向测井响应的有限元法模拟[J].中国传媒大学学报(自然科学版),2012,19(3):16-24.
[6]仵杰,谢尉尉,解茜草,等.水平磁偶极子在薄交互地层中的电流流动特性分析[J].国外测井技术,2013,33(1):11-13.
(编辑:杨友胜)
Research on log response correction method of sheet resistivity
Wang Xin and Pan Yuzhou
(Research Institute of Petroleum Exploration and Development,East China Company,SINOPEC,Nanjing,Jiangsu 210011,China)
Limited to longitudinal resolution of apparatus,surrounding rock has great effects on log response of resistivity when res⁃ervoir thickness is less than 2 m.It is difficult to direct react real resistivity of target strata.Through finite element(FEA)numerical simulation method,electric logging response value of different reservoir thickness(0.1~10 m)was simulated.Take real strata resis⁃tivity and its ratio to determine correction coefficient(CF)of reservoir resistivity.On this basis,correction chart of electric logging response under different reservoir thickness was compiled.After using correction chart,examples of block G in North Jiangsu oil⁃field show that sheet resistivity is closer to the true formation resistivity.
thin bed,electric logging response,finite element(FEA)
P631.821
A
2015-04-29。
王欣(1985—),男,博士,工程师,地球物理测井。
国家自然科学基金重点项目(编号:11134011)资助。

