多跨转子系统耦合故障定量诊断方法

许 琦， 吴 昊， 赵立超， 姚红良， 闻邦椿

(1.东北大学机械工程与自动化学院， 辽宁 沈阳 110819；2.沈阳鼓风机集团安装检修配件有限公司技术工程部， 辽宁 沈阳 110869)

多跨转子系统耦合故障定量诊断方法

许 琦1， 吴 昊1， 赵立超2， 姚红良1， 闻邦椿1

(1.东北大学机械工程与自动化学院， 辽宁 沈阳 110819；2.沈阳鼓风机集团安装检修配件有限公司技术工程部， 辽宁 沈阳 110869)

以有限元理论和谐波平衡理论为基础分析多跨转子系统的动态特性并提出多跨转子系统耦合故障定量诊断方法。利用故障前后转子系统的振动响应,各次谐波分量与系统剩余量方程的频率响应矩阵之间的关系推导诊断理论并获得诊断方程，以转-定子碰摩和联轴器不对中耦合故障为例建立多跨转子系统和实验台转子系统的有限元模型，通过数值仿真和转子实验台实验准确地诊断出故障位置，验证方法的有效性和稳健性。通过同一转速下故障前后转子系统至少n+1个测点的振动响应数据可以在线确定具有n个耦合故障转子系统的故障位置。对于转子系统的主要振动故障，如碰摩、不对中、裂纹等，诊断方法具有良好的适用性。

故障诊断； 多跨转子系统； 耦合故障； 谐波分量； 剩余量方程

引 言

转子系统作为旋转机械的核心部件，常常出现各种单一或耦合的振动故障，如质量不平衡、联轴器不对中、转-定子碰摩、裂纹、轴承和支承故障等，不仅影响其正常工作，严重时会发生机毁人亡的事故，造成重大的损失[1-2]。及时发现并掌握故障信息，对于处理这些故障有着重要的意义。

目前，学者对于转子系统的故障诊断做了大量的研究，主要分为两类方法：一类是非模型的故障诊断方法，另一类是数学模型的诊断方法。

非模型的诊断方法如振动信号分析方法、模态和信息处理方法，人工智能、专家系统的诊断方法，神经网络的诊断方法等。将测量的振动信号进行滤波和去噪，经过各种信号处理技术，如快速傅里叶变换(FFT)、小波变换(WT)、经验模态分解(EEMD)和Hilbert-Huang变换等，进行转子系统的各种故障诊断[3]。如Hongkai Jiang等[4]提出多小波包改进的经验模态分解(EEMD)法的旋转机械多重故障诊断方法，提高了分解结果的精度和准确性；Jimeng Li等[5]利用随机共振(SR)法增强非线性系统中的微弱信号，诊断淹没在噪声中的微弱信号，提出了Morlet小波变换利用噪声控制的二阶增强随机共振法进行故障诊断；Long Zhang等[6]采用多尺度熵(MSE)和自适应的神经模糊推理系统(ANFIS)诊断轴承故障，此方法不仅能可靠地分离不同故障类别，而且能够识别故障严重程度；Yaguo Lei等[7-8]提出统计分析、改进的距离评估技术和自适应的神经模糊推理系统(ANFIS)的智能故障诊断方法，并应用在滚动轴承的故障诊断。

目前多数故障诊断方法是非模型的诊断方法，能够诊断出故障的存在、类型及估算出故障所在位置，在精度要求不高的前提下信号分析方法直接、有效，但需要精确诊断的时候，难以达到故障位置的定量诊断。

数学模型的诊断方法即利用转子系统动力学特性及振动信号相结合进行故障诊断的方法，能够诊断出故障的具体位置，以及时准确地处理严重故障[9]。如Arun Kr Jalan等[10]提出一种基于模型的转子系统不对中和质量不平衡故障诊断方法，采用剩余量生成法结合振动信号，得到故障状态特性和故障位置；Mohit Lal等[11]提出受迫响应信息的频域最小二乘法拟合技术诊断算法估计汽轮发电机系统模型的多重故障参数，并具有一定的抗噪声影响能力；A S Sekhar[12]提出一种基于有限元模型的在线诊断转子裂纹故障的方法，采用等效力和剩余振动量的数学模型，结合信号分析方法快速傅里叶变换(FFT)得出裂纹的位置和特性；G N D S Sudhakar等[13]采用等效力最小化方法和振动最小化方法相结合诊断转子系统不平衡故障位置和严重程度，解决了多故障参数下较少振动测量值的问题；姚红良等[14]根据碰摩故障转子系统中任意两节点之间高次谐波分量之比等于无故障转子系统频率响应矩阵的相关元素之比的关系，利用广义等效力、剩余振动量和谐波平衡理论提出了诊断转子系统单碰摩故障的方法。

数学模型的诊断方法精度高，能够将转子系统的故障诊断具体到“点”上，同时可以得到一些故障的严重程度，但根据作者的了解，目前或仅对转子系统单故障进行诊断，或加速度、速度和位移响应均需测量，或仅利用工频响应而忽视二倍频、三倍频等高频响应等，有一定的缺陷和不足。

本文的目的是建立基于模型的多跨转子系统耦合故障定量诊断方法。首先，利用位移振动信号的振幅、频率和相位信息以提高诊断精度；其次，结合有限元理论和谐波平衡理论，利用故障转子系统的振动响应各次谐波分量与系统剩余量方程的频率响应矩阵之间的关系，推导并建立诊断方程；第三，利用有限元模型中一些节点的位移响应诊断出故障位置节点；最后，通过数值仿真和实验验证诊断方法的有效性和稳健性。

1 转子系统动力学模型

典型的转子系统由一些离散的叶轮、具有分布质量及弹性的轴段和轴承座等部件组成，将系统离散成由刚性圆盘、轴段等单元连接成的模型，各个单元间在节点处联接，忽略转子系统的轴向变形。弹性轴段单元的广义坐标分别为两端节点的位移的转角，如图1所示，其复数表示为

(1)

图1 轴段单元的有限元模型Fig.1 Finite element model of shaft unit

将多跨转子系统离散成具有N个节点、N-1个单元组成的有限元动力学模型，其整体动力学方程为

(2)

式中M为整体质量矩阵;C=D+ωG，D为整体阻尼矩阵，G为陀螺力矩矩阵，ω为转子转速;K为整体刚度矩阵，矩阵为2N×2N阶对角方阵，具体形式参见文献[15];u为振动响应矢量;F为质量不平衡引起的外激励矢量。

(3)

2 定量诊断方法

式(3)-(2)，得

(4)

当系统稳定运行，故障激励，也就是各广义故障力包含谐波分量时，系统的响应也包含各次谐波分量，故可以将Δu展开成各阶谐波分量和的形式，即

(5)

式中 Δuiejiωt为Δu的第i阶谐波分量。

将广义故障力也展开成各阶谐波分量和的形式，即

(6)

式中Aiejiωt，Biejiωt，…，Niejiωt分别为广义故障力的第i阶谐波分量。

根据谐波平衡理论[16]，有

(7)

(8)

由式(8)就可以定量计算多跨故障转子系统的故障位置。设多跨转子系统任意两个节点k1和k2，有

E(2k1-1,2L2-1)(jlω)Bl+…+E(2k1-1,2Ln-1)(jlω)Nl]/

[E(2k2-1,2L1-1)(jlω)Al+E(2k2-1,2L2-1)(jlω)Bl+

…+E(2k2-1,2Ln-1)(jlω)Nl]

(9)

式中 相关参数Al，Bl，…，Nl由下式求解。

(10)

对于具有n个故障的转子系统，相关参数也有n个，即需要n个节点的响应。

将转子系统所有节点号Li分别代入式(9)中计算δL1L2…Ln，当δL1L2…Ln的绝对值最小时，此时的L1，L2，…，Ln的取值即为转子系统的故障节点位置。即定量诊断n个故障节点位置至少需要n+1个节点的振动响应。

3 诊断计算步骤

本方法的具体计算步骤如下：

当多跨转子系统有n个耦合故障时

(1)分别测量转子系统故障发生前n+1个点的振动响应；

(2)分别测量转子系统故障发生后同一n+1个点的振动响应；

(3)计算响应剩余量并展开成谐波分量和的形式；

(4)计算频率响应函数矩阵；

(6)求解相关参数Al，Bl，…，Nl；

(7)将转子系统所有节点号Li分别代入计算δL1L2…Ln；

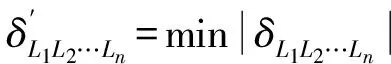
4 数值仿真

4.1 简单多跨转子模型

建立多跨转子系统的有限元模型，如图2所示。

具体参数如下：将整体转子系统划分为52个单元，即有53个节点，弹性模量E=210 GPa；其中轴段直径d=10 mm，长度l=20 mm；圆盘直径d1=80 mm，长度l1=10 mm；将联轴器简化为当量轴段，直径d2=20 mm，长度l2=10 mm；将支承视为等刚度弹性支承，支承刚度为k=1×106N/m；质量偏心位于节点9和30处，不平衡质量me=5×10-6kg，偏心距e=2 mm，不平衡相位为0。

假设此转子系统的故障为定-转子碰摩和联轴器不对中耦合故障。碰摩故障模型如图3所示，位于节点26处，故障力的表达式见文献[17]，碰摩刚度krub=2×105N/m，碰摩间隙erub=2.5 μm，碰摩类型为局部碰摩，碰摩角度为0°≤θ≤45°。

图2 多跨转子系统的有限元模型Fig.2 Finite element model of multi-span rotor system

图3 碰摩力模型Fig.3 Model of rub force

联轴器不对中故障模型如图4所示，位于节点17处，故障力的表达式见文献[10]，初始不对中量为Δx0=5 mm，α0=2°。

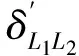
和节点17

图4 不对中力模型Fig.4 Model of misalignment force

图5 诊断结果Fig.5 Diagnosis result

4.2 支承刚度和振动响应影响分析

假定实际支承刚度为k=1×106N/m，而诊断时采用的支承刚度为k=1×1010N/m，数值模拟实验得到的结果如图6所示，碰摩位置和不对中位置仍分别在节点26和节点17处，即支承刚度的变化对本诊断方法几乎没有影响。

假定实际情况测得的振动响应不准确，其数值服从方差为0.05的正态分布，分别取2，3，4和5阶谐波分量进行总计400次仿真计算，得出的结果如图7所示。其中碰摩故障位置所在的节点26的准确率在56%；不对中故障位置所在节点17的准确率在72%，均远高于其他节点所占的百分比，可见此时仍可以诊断出耦合故障的大致位置，表明此方法具有很好的稳健性。

图6 支承刚度不准确时的诊断结果Fig.6 Diagnosis result when support stiffness is not accurate

图7 振动响应数据不准确时的诊断结果Fig.7 Diagnosis result when vibration response data is not accurate

4.3 工程多跨转子实例

建立某大型空分设备压缩机-汽轮机转子系统的有限元模型，如图8所示。

图8 压缩机-汽轮机转子系统模型Fig.8 Finite element model of compressor-turbine rotor system

具体参数如下：将整体转子系统划分为136个单元，即有137个节点；转子总长14 880 mm；偏心me=16 kg·m位于节点28和98处；工作转速为4 000 r/min；滑动轴承支承，分别在节点4，65，72和120处，其动力学方程见文献[15]。

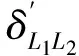
图9 诊断结果Fig.9 Diagnosis result

5 实 验

本方法的实验验证在Bently转子实验台上完成，利用B&K3560B信号采集器采集并处理信号。实验设备及其有限元模型如图10所示，转子模型由2个圆盘、38个轴段单元、2个支承及1个联轴器组成，尺寸参数如表1所示。

4个位移传感器分别放置在节点9，15，21和31处，碰摩和不对中故障分别加在节点16和联轴器(节点37～43)上，在转速为2 400 r/min时采集振动数据并处理，其中节点15的故障响应曲线如图11所示，信号中有明显了高倍频出现。

图10 实验设备及其有限元模型Fig.10 Experimental equipment and finite element model of Bently rotor test rig

参数名称数值单元数42节点数43弹性模量/GPa210单元的直径和长度/mmds=10，ls=15圆盘的直径和厚度mmdd=75，ld=25节点1与2之间的长度/mmls1=20节点11与12，14与15，22与23，25与26之间的长度/mmls2=17．5联轴器长度/mmlc=61

图11 节点15的故障响应曲线Fig.11 Response curve on node 15

诊断结果如图12所示，图中显示最小值的坐标为(16,37)，因此，碰摩和不对中故障分别在节点16和37处。诊断方法成功地诊断出了故障位置。

图12 诊断结果Fig.12 Diagnosis result

6 结 论

(1)本文提出多跨转子系统耦合故障定量诊断方法，并以碰摩和不对中耦合故障多跨转子为例进行故障诊断，通过数值仿真和实验成功地将故障定位在“点”上，验证了方法的有效性和稳健性；

(2)对于具有n个耦合故障的多跨转子系统，仅需同一转速下故障发生前后的n+1个点的振动响应数据即可诊断，方法简单；

(3) 诊断方法适用于各种具有局部故障的转子系统中，即在微分方程中体现为某点存在周期性的广义故障力，诊断方法对转子系统的主要故障如转子不平衡、碰摩、不对中、裂纹、轴承及支承等均具有良好的适用性。

[1] 闻邦椿，顾家柳，夏松波，等. 高等转子动力学[M]. 北京:机械工业出版社, 2000.

[2] 韩清凯，于涛，王德友，等. 故障转子系统的非线性振动分析与诊断方法[M]. 北京:科学出版社, 2010.

[3] Feng Z P, Liang M, Chu F L. Recent advances in time-frequency analysis methods for machinery fault diagnosis: A review with application examples[J]. Mechanical Systems and Signal Processing, 2013, 38(1):162—205.

[4] Jiang H K, Li C L, Li H X. An improved EEMD with multiwavelet packet for rotating machinery multi-fault diagnosis[J]. Mechanical Systems and Signal Processing, 2013, 36(2):225—239.

[5] Li J M, Chen X F, Du Z H, et al. A new noise-controlled second-order enhanced stochastic resonance method with its application in wind turbine drivetrain fault diagnosis[J]. Renewable Energy, 2013, 60:7—19.

[6] Zhang L, Xiong G L, Liu H S, et al. Bearing fault diagnosis using multi-scale entropy and adaptive neuro-fuzzy inference[J]. Expert Systems with Applications, 2010, 37(8):6 077—6 085.

[7] Lei Y G, He Z J, Zi Y Y. A new approach to intelligent fault diagnosis of rotating machinery[J]. Expert Systems with Applications, 2008, 35(4):1 593—1 600.

[8] Lei Y G, He Z J, Zi Y Y, et al. Fault diagnosis of rotating machinery based on multiple ANFIS combination with GAs[J]. Mechanical Systems and Signal Processing, 2007, 21(5):2 280—2 294.

[9] Lees A W, Sinha J K, Friswell M I. Model-based identi?cation of rotating machines[J]. Mechanical Systems and Signal Processing, 2009, 23(6):1 884—1 893.

[10]Jalan A K, Mohanty A R. Model based fault diagnosis of a rotor-bearing system for misalignment and unbalance under steady-state condition[J]. Journal of Sound and Vibration, 2009, 327(3-5):604—622.

[11]Lal M, Tiwari R. Multi-fault identification in simple rotor-bearing-coupling systems based on forced response measurements[J]. Mechanism and Machine Theory, 2012, 51:87—109.

[12]Sekhar A S. Crack identification in a rotor system: a model-based approach[J]. Journal of Sound and Vibration, 2004, 270(4-5):887—902.

[13]Sudhakar G N D S, Sekhar A S. Identification of unbalance in a rotor bearing system[J]. Journal of Sound and Vibration, 2011, 330(10):2 299—2 313.

[14]姚红良，韩清凯，李凌轩，等. 基于谐波分量的转子系统碰摩故障定量诊断方法[J]. 机械工程学报，2012, 48(5):43—48.

Yao Hongliang, Han Qingkai, Li Lingxuan, et al. Method for detecting rubbing fault in rotor system based on harmonic components[J]. Chinese Journal of Mechanical Engineering, 2012, 48(5):43—48.

[15]钟一谔，何衍宗，王正,等. 转子动力学[M]. 北京：清华大学出版社, 1987.

[16]Grollg V, Ewins D J. The harmonic balance method with arc-length continuation in rotor/stator contact problems[J]. Journal of Sound and Vibration, 2001, 241(2):223—233.

[17]Zhang W M, Meng G, Chen D, et al. Nonlinear dynamics of a rub-impact micro-rotor system with scale-dependent friction model[J]. Journal of Sound and Vibration, 2008, 309(3/5):756—777.

Quantitative coupling fault diagnosis method of multi-span rotor based on harmonic components

XUQi1,WUHao1,ZHAOLi-chao2,YAOHong-liang1,WENBang-chun1

(1.School of Mechanical Engineering and Automation, Northeastern University, Shenyang 110819, China; 2.The Engineering Department, Shenyang Blower Works Group Corporation Installation Accessories Co., LTD., Shenyang 110869, China)

A model based method for online quantitative multi-fault diagnosis of multi-span rotor system is presented. Based on finite element method and harmonic balance theory, the dynamic characteristics of the rotor system are analyzed, and the relationship between the harmonic components of vibration responses and the frequency response matrix of residual equation in the fault rotor system is used to derive diagnosis theory and equation. The finite element model of a multi-span rotor system with rub-impacts and coupling misalignment faults is established. The effectiveness and robustness of the proposed method is verified by numerical simulation and then by test rig experiment. The advantage of the proposed method is that n fault locations can be detected on line by using at least vibration response data onn+1 nodes of rotor system before and after faults occur at the same rotating speed, and also the method has a good applicability for detecting the main vibration faults in rotor system such as rub-impact, misalignment and cracks.

fault diagnosis; multi-span rotor system; coupling fault; harmonic component; residual equation

2013-11-12；

2015-01-04

国家重点基础研究发展计划项目(2011CB706504);国家自然科学基金资助项目(51005042);中央高校基本科研业务费专项资金资助项目(N100403005)

TH165+．3； TK267；

A

1004-4523(2015)03-0495-08

10.16385/j.cnki.issn.1004-4523.2015.03.021

许琦(1985—)，男，博士研究生。电话:13804063247；E-mail:xuqi-010904@126.com