含凸轮-滚轮机构的准零刚度系统隔振特性实验研究
周加喜, 王心龙, 徐道临,2, 张 敬
(1.湖南大学机械与运载工程学院,湖南 长沙 410082; 2.汽车车身先进设计制造国家重点实验室,湖南 长沙 410082)
含凸轮-滚轮机构的准零刚度系统隔振特性实验研究
周加喜1, 王心龙1, 徐道临1,2, 张 敬1
(1.湖南大学机械与运载工程学院,湖南 长沙 410082; 2.汽车车身先进设计制造国家重点实验室,湖南 长沙 410082)
提出了一类含凸轮-滚轮机构的准零刚度隔振器,进行了静力学分析,给出了具有分段非线性的回复力;建立了隔振系统的运动方程,并利用谐波平衡法得到了主共振响应的一次近似解析解,给出了凸轮-滚轮保持接触的参数条件,并分析了保持接触情况下的力传递率;最后,对准零刚度隔振系统进行了激振实验分析,测定了不同工况下的力传递率,并与相应的线性系统进行了对比。结果表明:通过引入凸轮-滚轮负刚度机构,有效降低了起始隔振频率,抑制了共振,提高了隔振效果,因此,该准零刚度隔振器具有良好的低频隔振性能;在凸轮-滚轮保持接触的前提下,激励幅值越大,负刚度机构越易发挥作用,隔振效果更显著。
准零刚度; 低频隔振; 负刚度机构; 力传递率; 激振实验
引 言
准零刚度隔振技术是一种非常有代表性的低频隔振技术。它利用正负刚度并联组合,获得高静刚度低动刚度,既可承受较大静载,又能实现很低的自振频率,非常有利于低频隔振。关于准零刚度隔振技术的研究最早要追溯到上世纪80年代,Alabuzhev等[1]将正刚度弹性元件与负刚度弹性元件并联研发了若干隔振装置,并提出了准零刚度的概念。Carrella等[2,3]将螺旋弹簧进行几何组合,得到了准零刚度隔振器,并对其理论进行了系统而深入的研究。Platus[4]将在轴向载荷作用下表现负刚度特性的纵向弯曲梁与螺旋弹簧并联,设计出一种准零刚度结构。Le和Ahn[5]将此项技术应用于汽车座椅的隔振,针对低频和随机路面激励,取得了很好的效果。此外,Robertson等[6]基于高静刚度低动刚度理念,利用磁力弹簧实现了低频隔振。刘兴天等[7]将具有负刚度特性的欧拉屈曲梁结构与螺旋弹簧并联,设计准零刚度隔振器,并讨论了激励幅值对其隔振特性的影响。上述研究均表明:由于准零刚度隔振系统具有渐硬非线性特性,为确保系统的隔振性能,要求激励不能太大,且激励越小,隔振效果越好。然而,之前的实验研究[8,9]发现,当激励较小时,系统振动幅值较小,此时负刚度机构并没有参与其中,隔振性能与相应的线性系统相当,其优越性并没有体现出来。为了使负刚度机构对小位移更加敏感,本文将文献[5]中准零刚度隔振器的连杆用滚轮-凸轮机构代替,提出一种新型准零刚度隔振器,并对其静力学、动力学特性进行分析,为评估实际隔振性能,进行一系列的实验分析。
1 设计模型与力学特性分析
带滚轮-凸轮装置的准零刚度隔振器的设计图如图1所示。静载作用下系统处于静平衡位置,滚轮圆心与凸轮圆心在同一水平线上,水平弹簧和竖直弹簧的压缩量分别是δ和Δx=Mg/kv。当系统在平衡位置附近振动时,凸轮离开平衡位置,带有滚轮的水平弹簧与凸轮组成的机构在竖直方向产生负刚度,从而抵消竖直弹簧的正刚度。当负刚度与正刚度相等时,系统在平衡位置处的刚度将为零,即零刚度条件。

图1 准零刚度隔振器机构示意图Fig.1 Schematic diagram of the quasi-zero stiffness vibration isolator
本设计的一大优势在于其良好的可调性。通过水平调节轴可调节水平弹簧预压缩量,使之满足零刚度条件。当被隔振质量过大或过小时,通过调节卧式轴支撑在导杆中的位置,可使滚轮圆心与凸轮圆心连线始终处于水平。
1.1 静力学分析
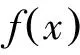
(1)

图2 准零刚度系统受力分析图(a)与滚轮的三种典型的相对位置(b)(c)(d)Fig.2 Schematic diagram of static analysis (a) and three typically relative positions between the cam and the roller (b) (c) (d)
式中kv为竖直弹簧刚度,kh为水平弹簧刚度。r1为滚轮半径,r2为凸轮半径。

(2)

(3)

(4)

图3 当β=0.266时系统的无量纲刚度曲线Fig.3 Non-dimensional stiffness of the system when β=0.266
因此,当刚度比确定后,通过调节四个水平弹簧的预压缩量,可以使得准零刚度隔振器在平衡位置产生零刚度。
将零刚度条件(4)分别代入到式(2)和(3),可得准零刚度隔振系统的无量纲回复力和刚度
(5)
(6)
考虑脱开的情况,准零刚度隔振器的无量纲回复力可完整地写为
(7)
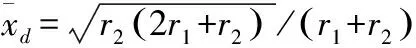
(8)

1.2 动力学分析

(9)

(10)
传递到基础的力可以表示成
(11)
力传递率为
(12)
由于方程(10)存在多解,在跳跃区间内传递率存在三个解。根据文献[3]的研究,上跳频率与下跳频率可以近似地写成
(13)
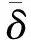
2 数值仿真分析
2.1 凸轮-滚轮保持接触的参数条件
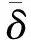

图4 振幅最大值Amax关于参数ζ和0的曲面图Fig.4 3D figure of Amax with respect to system parameters ζ and 0

图5 滚轮与凸轮接触和脱开的参数区间Fig.5 Parameter regions that the roller keeps contact with the cam or disengages with the cam
2.2 力传递率
图6还描述了激励幅值对准零刚度系统的隔振性能的影响。可以看出,随着激励幅值的增加,下跳频率增加,与式(14)描述一致。虽然,随激励幅值增加,低频隔振性能有所恶化,但当激励幅值在图5所示的灰色区域时,准零刚度系统的隔振性能始终优于线性系统。

图6 准零刚度隔振系统力传递率及与线性系统的对比Fig.6 Force transmissibility of QZS vibration isolation system compared with the linear system
3 实验研究
3.1 实验装置与测试设备
准零刚度隔振器实验装置及测试设备如图7所示。它主要由准零刚度隔振器、激振器、力传感器(2个)、功率放大器、数据采集与分析仪组成。其中一个力传感器安装于配重与激振器之间,用于测激励力;另一个力传感器安装在支撑基座上,用于测量振动过程中传递到基础上的力。数据采集与分析仪用于采集力传感器的输入输出信号。配重固定于承重台上,在激励力的作用下沿导杆在竖直方向上运动。导杆上端固定于承重台,下端套于底座上的线性轴承中,起导向作用,保证配重沿竖向运动。线性轴承可以减少运动件之间的摩擦,从而减少阻尼因素对系统隔振效果的影响。

图7 实验装置与测试设备图Fig.7 Photograph of prototype of QZS vibration isolator and experimental apparatus
数据采集仪内置信号发生器输入正弦信号,经功率放大器放大,驱动激振器提供竖向激振力,可通过功放调节激励幅值、频率等参数。力传感器拾取输入输出信号,并传递给数据采集分析仪,从而得到激振力与传递至基础的传递力的时程响应,进而可计算力传递率,并评价系统的隔振性能。
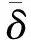

表1 实验装置的物理参数
激振器输入正弦激励,激励频率带宽从1到50 Hz。需要说明的是,在整个实验过程中难以保持恒定的激励幅值。在低频区域,振幅较大,易损坏激振器,因此输入较小的激励幅值。在实验过程中,系统在低频区域的激励力是渐变的,一旦系统的振动处于安全的范围内,激励的幅值便可设定为一定值。
为测试准零刚度系统在不同激励下的隔振性能,采用两组不同的激励幅值进行激振,测试所用的激励频率及相应的幅值如表2所示。从第一组激励幅值可以看出,在激励频率1~5 Hz区间激励力持续增加至45 N,然后保持不变;第二组1~7 Hz区间内激励幅持续增加至82 N,然后保持不变。
测试相应线性系统的力传递率时,只需将准零刚度隔振装置的滚轮-水平弹簧装置移除即可。
表2 正弦激励的频率及其有效值
Tab.2 The frequency and RMS value of the sinusoidal excitation signal used in experiment

激励频率/Hz第一组激励/N第二组激励/N19.3868.7921.58.2548.45727.42310.4072.59.50111.315316.88813.9973.520.67825.712428.52435.6684.531.47640.17954542.2755.54545.31164542.9027~504582
力传递率一般定义为传递至基础的脉动力的幅值与激励幅值的比值,但因准零刚度隔振系统为强非线性系统,其响应可能出现诸如混沌等复杂动力学响应。因此,用响应与激励的均方根(有效值)的比值来定义实验测定的力传递率[10-11]
(14)
3.2 实验结果
图8(a)为施加第一组激励时隔振系统的力传递率曲线。准零刚度隔振系统的实验结果用实线表示,线性系统的实验结果用虚线表示。结果表明:准零刚度系统起始隔振频率约为3.5 Hz,而相应线性系统约为6 Hz;在线性系统共振频率4 Hz附近,准零刚度系统的力传递率比线性系统小很多,约为线性系统的14%,且准零刚度系统力传递率峰值明显低于线性系统;高频区域(大于线性系统的起始隔振频率)除个别频率外,力传递率均小于线性系统,这一实验现象在之前的连杆式或斜弹簧式准零刚度隔振实验[8-9]中均未出现过。因此,通过引入凸轮-滚轮机构,并设计参数使之满足零刚度条件,不仅可降低起始隔振频率,改善线性系统的隔振性能,实现低频隔振,且其隔振效果(尤其是高频)优于已有的准零刚度隔振器。
准零刚度隔振装置是一个比较复杂的机构,且含有柔性较大的支撑基座,尽管在实验中,将支座尽量布置在基座中间,且在滑轨间放置条形砝码,尽量增加底座的刚度,但不可避免系统高阶模态被激发出来,因此,图8准零刚度隔振系统传递率曲线在约17 Hz附近出现峰值,但仍小于1,具有隔振效果。
图8(b)展示了分别作用第一和第二组激励时的力传递率曲线,可以看出,随着激励幅值的增加,准零刚度系统的隔振效率提高,尤其是在高频区域。
为进一步分析激励幅值对准零刚度系统传递率的影响,将激励频率调至10 Hz,调节功放使激励幅值逐渐增大,测量力传递率,给出力传递率随激励幅值变化的曲线,如图9所示。可以看出,随激励幅值增加,力传递率降低,隔振性能提高,这与之前的实验观察一致[8-9]。当激励较小时,系统振动幅值较小,此时负刚度机构未起作用,其优越性并未体现出来。而当激励较大时,负刚度机构充分发挥作用,有效提高了系统的隔振性能。


图8 第一组激励力下准零刚度系统的实测力传递率
Fig.8 Force transmissibility by experimental tests of the QZS vibration isolation system under the first group excitations

图9 激励力幅值对传递率的影响Fig.9 Effects of exciting amplitude on the force transmissibility
4 结 论
针对低频隔振,设计了一种含凸轮-滚轮负刚度机构的准零刚度隔振器,通过静力分析给出了零刚度参数条件;利用谐波平衡法得到了系统响应的一次谐波解,并近似地给出了凸轮与滚轮保持接触的参数区间;最后通过实验分析评估了系统的隔振性能。得出如下结论:(1)激励幅值小于一定值时,凸轮-滚轮始终保持接触,准零刚度隔振系统的起始隔振频率低于相应的线性系统,且隔振效率优于线性系统;(2)凸轮-滚轮保持接触的情况下,激励幅值越大,隔振效果越好。
[1] Alabuzhev P, Gritchin A, Kim L, et al. Vibration Protecting and Measuring System with Quasi-zero Stiffness[M]. New York:Taylor & Francis,1989.
[2] Carrella A, Brennan M J, Waters T P. Static analysis of a passive vibration isolator with quasi-zero-stiffness characteristic[J]. Journal of Sound and Vibration, 2007, 301(3-5): 678—689.
[3] Carrella A, Brennan M J, Kovacic I, et al. On the force transmissibility of a vibration isolator with quasi-zero-stiffness[J]. Journal of Sound and Vibration, 2009, 322(4-5): 707—717.
[4] Platus D L. Negative-stiffness-mechanism vibration isolation systems[A]. Proceedings of SPIE- the International Society for Optical Engineering[C]. Denver, Cdorado, USA, 1999, 3 786: 98—105.
[5] Le T D, Ahn K K. A vibration isolation system in low frequency excitation region using negative stiffness structure for vehicle seat[J]. Journal of Sound and Vibration, 2011, 330(26): 6 311—6 335.
[6] Robertson W S, Kidner M R F, Cazzolato B S, et al. Theoretical design parameters for a quasi-zero stiffness magnetic spring for vibration isolation[J]. Journal of Sound and Vibration, 2009, 326(1-2): 88—103.
[7] 刘兴天, 黄修长, 张志谊, 等. 激励幅值及载荷对准零刚度隔振器特性的影响[J].机械工程学报, 2013, 49(6): 89—94.
Liu X T, Huang X C, Zhang Z Y, et al. Influence of excitation amplitude and load on the characteristics of quasi-zero stiffness isolator[J]. Journal of Mechanical Engineering, 2013, 49(6): 89—94.
[8] Xu D L, Yu Q P, Zhou J X, et al. Theoretical and experimental analysis of a nonlinear magnetic vibration isolator with quasi-zero-stiffness characteristic[J]. Journal of Sound and Vibration, 2013, 332(14): 3 377—3 389.
[9] Xu D L, Zhang Y Y, Zhou J X, et al. On the analytical and experimental assessment of performance of a quasi-zero-stiffness isolator[J], Journal of Vibration and Control, 2014, 20(15): 2 314—2 325.
[10]Ravindra B, Mallik A K. Performance of non-linear vibration isolators under harmonic excitation[J]. Journal of Sound and Vibration, 1994, 170(3): 325—337.
[11]Lou J J, Zhu S J, He L, et al. Experimental chaos in nonlinear vibration isolation system[J]. Chaos, Solitons & Fractals, 2009, 40(3):1 367—1 375.
Experimental study on vibration isolation characteristics of the quasi-zero stiffness isolator with cam-roller mechanism
ZHOUJia-xi1,WANGXin-long1,XUDao-lin1,2,ZHANGJing1
(1.College of Mechanical and Vehicle Engineering, Hunan University, Changsha 410082, China; 2.State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Changsha 410082, China)
quasi-zero stiffness isolator with cam-roller mechanism was proposed, and the corresponding piecewise nonlinear restoring force was obtained by static analysis. The equation of motion of the vibration isolation system was established, and the first approximation of primary resonance was achieved by Harmonic Balance method. Moreover, the parametrical regions, where the cam always keeps in touch with the roller, and the force transmissibility were given based on approximate solutions. Finally, experiments were carried out to evaluate force transmissibility under excitations of various frequencies, which were compared with those of the corresponding linear vibration isolation system. The results show that the cam-roller mechanism with negative stiffness lowers the starting isolation frequency and enhances the isolation efficiency, and suppresses the resonant response, leading to an excellent low-frequency vibration isolation performance. Also shown is that, under the condition of keeping in touch between the cam and the roller, the larger the excitation amplitude is, the more likely to reduce the system's stiffness the negative-stiffness mechanism is, and the better the vibration isolation effect is.
quasi-zero stiffness; low-frequency vibration isolation; negative-stiffness mechanism; force transmissibility; exciting experiment
2014-03-28;
2014-07-28
国家自然科学基金资助项目(11102062);高等学校博士学科点专项科研基金(20110161120040);中央高校基本科研业务费资助项目
O328
A
1004-4523(2015)03-0449-07
10.16385/j.cnki.issn.1004-4523.2015.03.015
周加喜(1983—),男,博士,副教授,硕士生导师。电话:13975835883;E-mail: jxizhou@hnu.edu.cn

