基于局部平稳法的黏滞阻尼被动控制结构抗震可靠度分析

孙香红， 孔 凡， 李书进

(1.长安大学建筑工程学院， 陕西 西安 710061； 2.武汉理工大学土木工程与建筑学院， 湖北 武汉 430070)

基于局部平稳法的黏滞阻尼被动控制结构抗震可靠度分析

孙香红1， 孔 凡2， 李书进2

(1.长安大学建筑工程学院， 陕西 西安 710061； 2.武汉理工大学土木工程与建筑学院， 湖北 武汉 430070)

针对基于确定性激励的被动控制装置参数设计不具有普遍性的问题，提出了黏滞阻尼被动控制结构在一般非平稳随机地震动作用下抗震可靠度分析的局部平稳法。首先基于非平稳随机过程的局部平稳小波模型，提出了适用于临界阻尼比较大的黏滞阻尼被动控制结构的非平稳地震动输入-多自由度(受控)结构位移响应输出的功率谱关系。其次，根据超越过程的Markov过程假定及各阶响应谱矩，得到了受控结构层间位移的动力可靠度。数值分析结果表明：黏滞阻尼器在不同层间的配置，对受控结构的层间动力可靠度有显著影响。最后，以一个6层剪切型多自由度结构为例，对比了Monte Carlo模拟估计与本文所提方法计算的结构动力可靠度，验证了该方法的可靠性与高效性。

随机过程； 局部平稳法； 黏滞阻尼器； 被动控制； 抗震可靠度

引 言

自上世纪70年代初姚治平(J P T Yao)[1]提出关于结构振动控制的概念以来，结构控制已成为减小外荷载特别是灾害性环境作用下土木工程结构动力响应的有效手段之一。结构振动控制主要可分为主动、被动及半主动控制3种[2]。其中，被动控制技术以其构造简单、造价低廉、易于维护以及不需要外界能源等特点在实际工程中得到了广泛应用[3]。结构被动控制技术主要分为基础隔震、耗能减震以及调谐质量/液体阻尼(TMD/TLD)3大类。2013年4月发生的芦山地震，首次检验了国内隔震结构(芦山人民医院)的抗震可靠性。基础隔震技术最为成熟，但其存在隔震垫老化等问题且主要适合中低层结构；而TMD/TLD主要应用于高层或超高层结构的抗风设计，应用于抗震时有时甚至会出现负效应[3]。

耗能减震装置可分为黏滞液体阻尼器、黏弹性固体阻尼器、软钢耗能装置以及摩擦阻尼器等[4-5]。其中，黏滞液体阻尼器在上世纪90年代冷战结束经军事工业方面解密后，被迅速扩展应用于民用结构工程领域[6]。黏滞液体阻尼器以其较少提供平面内恢复力(几乎不改变结构动力特征)、建模简单(对于线性黏滞阻尼而言)以及在较大范围内为速度相关型(不依赖于加载频率及温度)等特点，引起了广泛的关注。在耗能减震结构设计中，减震效果的关键在于达到预期减震目标的阻尼器参数及位置分布设计。以往的研究和试验往往采取若干代表性实际地震动激励下的模型结构响应，以验证黏滞阻尼提供的减震效果[7]。然而，地震动等环境作用带来的荷载效应本质上是随机过程，故基于确定性激励的被动控制装置参数设计并不具有普遍性。因此，从概率意义上定量描述被动受控结构随机动力响应，研究达到概率意义上预期减震效果的阻尼器参数设置及位置分布，具有非常重要的理论和实用价值。

Pradlwarter和Schueller等人[8]利用Monte Carlo模拟得到了一致调制过滤白噪声作用下，摩擦阻尼控制线性结构的层间位移响应方差及动力可靠度；Guo和Xu等人[9]结合统计线性化方法计算了黏弹性阻尼装置下Bouc-Wen滞回结构在过滤白噪声作用下的随机响应，并建立了基于结构层间位移的动力可靠度计算方法；Guneyisi和Altay[10]针对随机地震动作用下加装黏滞阻尼的非线性高层钢筋混凝土结构，利用Monte Carlo模拟得到了4种破坏状态下的易损性曲线。为了考虑非线性黏滞性阻尼对结构的影响，Di Paola和Mendola等人基于统计线性化的思想得到了平稳随机过程激励下受控结构的等效线性阻尼[11-12]。孙广俊和李爱群[13]利用状态空间复模态分析的方法，在时域内推导了平稳过滤白噪声作用下，装有线性黏滞阻尼受控多自由度结构的层间位移响应二阶矩；更进一步，他们[14]利用相同的方法得到了安装线性黏滞阻尼的多自由度非线性结构层间位移首次超越概率；孙广俊和李爱群等[15]分析了双过滤白噪声平稳随机过程激励下，隔震装置和层间恢复力均为Bouc-Wen滞回模型时，基于层间位移的隔震结构体系可靠度指标；徐赵东[16]通过对装有黏弹性耗能系统结构运动方程的扩阶，得到了在平稳过程白噪声作用下线性多自由度结构的层间位移功率谱密度；李创第和夏立志等人[17]将黏滞阻尼器考虑为Maxwell模型，利用随机平均法计算了在一类具有Kanai-Tajimi谱的宽带过滤平稳白噪声作用下受控结构的响应概率密度解；孙香红等人[18]结合概率密度演化方法[19]计算了黏滞阻尼耗能减震结构的体系可靠度，并结合遗传算法得到了阻尼器在结构中的最优布置。

以上对耗能减震结构的随机动力分析，虽然从概率意义上得到了结构响应的一些概率特征，如响应统计值、概率密度或首超概率等，但大都采用了非平稳一致调制、甚至将平稳过滤白噪声作为结构激励。实际上，地震动过程不仅存在时域非平稳，而且存在频域非平稳，即其“瞬时”中心频率亦随着时间变化。因此，考虑同时具有时间-频率非平稳随机激励下多自由度结构的随机动力响应，为本文关键所在。

由Spanos和Kougioumtzoglou[20]最先提出的用于考虑激励频域非平稳性基于谐和小波分析的单自由度结构随机响应功率谱密度的计算方法(以下称局部平稳法)，能更好地应用于较大临界阻尼比的结构。随后，孔凡[21]及孔凡、Spanos与李杰等人将其扩展到了多自由度非线性滞回结构[22]。一般情况下，为了达到较好的减震效果，装备有黏滞阻尼器的结构，其等效临界阻尼比往往较大。因此，局部平稳法在黏滞阻尼耗能结构中的应用，可为计算受控结构随机动力响应开辟一条新的途径。

1 理论基础

1．1 广义谐和小波

广义谐和小波[23]是一种在时域上衰减较慢(依t-1)但在频域上紧支且具有时-频联合分析特征的谐和小波。在时域上它可以写为

(1)

式中T0为待分析信号的持时；(mj,nj)为广义谐和小波中用于表示第j阶小波的双指标因子；i为虚数符号；为了计算方便，认为每阶小波频宽ΔΩj=(nj-mj)Δω=(n-m)Δω相等；k=0,1,…,Nt-1为时间平移因子且Nt=n-m。将式(1)进行Fourier变换后，可得到广义谐和小波的“盒状”频域表达

(2)

1.2 非平稳随机过程的局部平稳广义谐和小波模型

最初由Nason等人发展的、基于非抽样小波函数的非平稳向量随机过程f(t)=[f1(t),f2(t),…,fnd(t)]T模型，即局部平稳小波(Local Stationary Wavelet,LSW)模型可以写为[24]

(3)

可以证明，当LSW模型中小波函数为广义谐和小波且各尺度小波频宽ΔΩj较窄时，式(3)进一步可表示为

(4)

(5)

式中f(mj,nj),k(t)为待分析信号在时间-频率子域[kT0/(n-m),(k+1)T0/(n-m))和[mjΔω,njΔω)上的子向量信号；A(mj,nj),k与B(mj,nj),k为nd×1维相互独立的0均值随机向量，且有下式成立

(6)

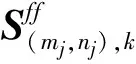
(7)

2 耗能减震结构的激励-响应功率谱关系

考虑在完全非平稳随机地震动作用下并可简化为剪切型集中质量模型的n维多自由度系统

(8)

式中M,C,K分别为nd×nd维质量、阻尼与刚度矩阵；M0=[m1,m2,…,mnd]T为nd×1维质量向量；当X(t)为nd×1维相对位移向量时，各系数矩阵为

(9)

一般地，结构阻尼矩阵可用Rayleigh矩阵表示，即

(10)

式中αc,βc为Rayleigh阻尼系数，可由前二阶振型阻尼比得到。

黏滞液体阻尼器性能试验表明，虽然精确的阻尼器数学模型可由Maxwell模型[7]描述，但对于大多数在地震或强风作用下振动频率较低的工程结构而言，液体黏滞阻尼器提供的附加刚度几乎可以忽略。因此，黏滞阻尼能在工程结构感兴趣的频率范围内提供仅依赖于层间速度的阻尼力，即

(11)

因此，设置有线性黏滞阻尼器的被动控制结构，在随机地震动作用下简化多自由度的集中质量模型为

(12)

式中Cd为黏滞阻尼器附加的阻尼矩阵，当阻尼器满布于各层间时，其形式与结构自身刚度矩阵一致，即

(13)

如将耗能减震系统随机动力位移响应和激励表示为下式的形式

(14)

同时注意到

(15)

式中C(mj,nj),k,D(mj,nj),k为0均值随机变量，且

(16)

(17)

可得

(18)

式中C=Cs+Cd为耗能减震结构总体阻尼矩阵，由原结构Rayleigh阻尼矩阵Cs和阻尼器附加阻尼矩阵Cd组成。将式(18)两式分别乘以它们的共轭转置并求期望，同时引入式(6)及式(16)可得

(19)

将式(19)化为简洁形式可得

(20)

式中

(21)

为局部时间-频率子域上的传递函数。

式(20)建立了在局部时-频子域上非平稳地震动功率谱与响应功率谱之间的关系。可见，式(20)与经典线性平稳随机振动分析激励与响应功率谱关系的相似程度。这一点不足为奇：由于对非平稳随机过程在时-频区间上的划分，同时假定在子时间区间上的局部平稳性，直接导致了如式(20)所示的功率谱关系式。基于如下判断，可认为局部平稳假定是合理的：对于大多数在随机地震动激励下的工程结构而言，由于激励相对于时间尺度T0/(n-m)的慢变性，从而使结构响应相对于此时间尺度也可认为是慢变的；更重要的是，尤其对于附加有一定阻尼装置的被动控制结构而言，阻尼器提供的等效临界阻尼比往往比原工程结构更大，从而使大阻尼比受控结构的瞬态响应可较快地耗散。

3 数值算例

为了验证局部平稳法在多自由度结构耗能减震中的应用效果，以一个算例进行分析。某6层框架结构，简化后可采用集中质量多自由度模型，其中各层集中质量、层间刚度系数以及相应模态频率如表1所示，黏滞阻尼器的线性黏滞阻尼系数取为2×105N·s/m。结构系统阻尼采用Rayleigh阻尼且前两阶模态阻尼比分别取为ζ1=0.05,ζ2=0.1。在其中两层对称设置4个阻尼器：不失一般性，可考虑阻尼器水平放置且忽略支撑刚度影响。为了考察不同阻尼器数目及分布情况对受控结构的随机动力响应概率特征的影响，考虑以下4种阻尼器位置分布情况：

(a) [1,1,1,1,1,1]； (b) [1,1,0,0,0,0]；

(c) [0,0,0,0,1,1]； (d) [0,0,0,0,0,0]

其中，以“1”表示该层间设置有黏滞阻尼装置，以“0”表示该层间无阻尼装置。

为了研究多自由度受控结构在完全时间-频率非平稳地震动作用下的随机动力行为， 假设地震动有形如

表1 各层质量与刚度参数

(22)

图1 完全非平稳地震动功率谱密度Fig.1 PSD of full non-stationary earthquake excitation

图2 非平稳地震动时程样本Fig.2 Sample excitation of non-stationary earthquake excitation

的非平稳功率谱密度[20-22]。根据《建筑抗震设计规范》(GB50011-2010)，调整谱强因子S0使相应的样本地震动时程峰值的均值为7度多遇情况时的0.35 m/s2。式(22)的功率谱密度如图1所示，所对应的非平稳地震动时程样本如图2所示，它由非平稳随机过程的谱表现方法生成[27]。由图1可见，此非平稳随机过程功率谱密度不仅沿时间轴表现出幅值非平稳性，而且沿频率轴也表现出频谱的非平稳性；由图2可见，随着时间的推移，样本时程除了幅值具有非平稳外，越零率也逐渐减小。

为了节约篇幅，本文只给出了阻尼器布置如a,b,c及d情况时的首层层间位移功率谱密度，如图3(a)～(d)所示；采用Monte Carlo模拟并进行非平稳随机过程功率谱估计[28]的结果如图4(a)～(d)所示。为了进一步显示二者的吻合度，图5(a)～(d)所示为局部平稳法与Monte Carlo模拟估计功率谱在典型时刻的“瞬时”功率谱对比。为了进一步显示局部平稳法在耗能减震结构中的适用程序，图6(a)～(d)所示为依据

(23)

计算得到的响应时变方差/标准差。

由图5(a)～(d)可知，局部平稳法能较好地给出受控结构的“瞬时”功率谱密度，但未能较好地把握未安装阻尼器时结构的“瞬时”功率谱密度，详见图5(d)。这种差别亦可由图6(a)～(d)可得，其中，除完全未安装阻尼器的结构外，局部平稳法均可较好地把握受控结构的时变响应标准差。造成局部平稳法在未安装阻尼器的小阻尼结构中的应用局限性的根本原因在于，随机激励和响应的局部平稳假定导致了能量只能在局部时间-频率子域上传递，却不能在局部时间-频率子域之间传递，文献[21]详细地阐述了这一点。正如引言中及第2节评论式(20)时所述，局部平稳法适用于具有较大阻尼系统的特性，可应用于被动耗能结构较大阻尼系数的情况，详可见图5(a)～(c)与图6(a)～(c)。

实际上，不同的阻尼器布置会给受控结构动力可靠度带来较大的影响[18]。为了证明这一点，本文采用超越过程Markov过程假定的动力可靠度计算方法[29-30]，并以层间位移首次超越某一预定限值为失效准则。按照《建筑抗震设计规范》(GB50011-2010)，钢筋混凝土结构的弹性层间位移角限值为1/550，且各层层高取为hi=3 m,i=1,2,…,6。图7表明了4种不同阻尼器布置的情况下由局部平稳法计算得出的各层间位移动力可靠度，并同时给出了直接Monte Carlo模拟样本2×104次的动力可靠度；详细结果以及二者之间相对误差的对比如表2所示。为了进一步验证二者之间的吻合程度，图8给出了各种阻尼器布置情况下结构首层层间时变动力可靠度。

图3 各阻尼器布置情况下局部平稳法计算所得底层层间位移功率谱密度Fig.3 Drift PSD of the 1st storey calculated by Local Stationary Method under different damper distributions

从表2可见，对于同一种阻尼器布置而言，随着楼层的增加，二种方法计算结果相对误差逐渐减小。不仅如此，对于不同阻尼器布置而言，可靠度越高的情况，二者之间的相对误差越小。由阻尼器布置情况a到阻尼器布置情况c，二者之间的最大相对误差均发生在第一层，分别为-0.313 1%，4.411 6%以及9.086 9%。因此，对于可靠度要求较高的工程结构而言，采用本文建议的方法计算得到的动力可靠度指标具有较高的精度。更重要的是，由于本文所建议方法仅涉及矩阵运算，并不要求多次求解动力微分方程，因此具有较高的计算效率。图8进一步证明了以上关于局部平稳法计算得到的动力可靠度精度随着可靠度的增加而提高的结论。不仅如此，图8显示了当结构未安装阻尼器时，局部平稳法给出的层间位移动力可靠度较Monte Carlo模拟偏大，这是与其得到的响应功率谱密度较Monte Carlo模拟偏小是密切相关的，具体原因可见文献[21]。

要使体系动力可靠度最高，可采取最小层间可靠度为评价指标进行阻尼器布置。由于被动阻尼总会消耗由地震动输入的能量，因此满布设置(情况a)得到的最小可靠度最高。当对称设置4个阻尼器在2个楼层时(阻尼器布置情况b与c)，在第1,2层设置阻尼器时的结构最小层间可靠度较设置阻尼器在第5和第6层时高。而较无阻尼器设置的情况而言(情况d)，前者能较均匀地提高各层间可靠度；后者仅对于设置有阻尼器的第5,6层能在很大程度上提高层间可靠度，这一点由第4,5层的层间可靠度突变即可看出。因此，在设置阻尼器数目一定的情况下，阻尼器布置与动力可靠度有紧密关系。当试图获取使结构最小层间可靠度最大的阻尼器布置时，对于简单的质量串联体系多自由度系统而言，即使采用枚举法亦不会造成较大的计算成本；而对于较为复杂的结构动力计算模型，尚需采用优化算法以得到动力可靠度意义上的最优布置设置。

4 结论与展望

针对目前耗能减震结构的阻尼器参数设置以及优化布置的研究中所存在的问题：采用确定性激励不具有一般代表性，采用平稳或一致调制随机过程作为激励不符合地震动的典型特征；同时结合局部平稳法在计算较大阻尼结构响应功率谱时的适用性，本文发展了一种确定黏滞阻尼受控结构在一般非平稳随机地震动作用下动力可靠度的方法——局部平稳法。首先，与Monte Carlo模拟估计的功率谱对比，本文所建议方法有较高的计算精度及计算效率；其次，与直接Monte Carlo模拟得到的结构层间动力可靠度对比表明：局部平稳法的计算精度随着可靠度的升高而提高；算例分析表明：不同阻尼器布置形式，对于结构层间动力可靠度有较大影响。总体而言，与其他经典方法如Markovian过程方法(FPK方程)以及Monte Carlo模拟方法对比，本文所建议方法在多自由度结构、非平稳激励以及计算效率方面更具优势。该方法亦可方便地扩展应用于考虑支撑刚度或阻尼刚度的Maxwell模型中。

图6 不同阻尼器布置情况下两种方法的首层位移标准差对比Fig.6 Standard deviation comparisons of the 1st floor drift between two methods under different damper distributions

图7 不同阻尼器布置情况下受控结构层间位移动力可靠度Fig.7 Dynamic reliabilities of storey drift of passive controlled structure under different damper distributions

图8 不同阻尼器布置情况下结构首层层间时变动力可靠度Fig.8 Time-varying dynamic reliability of the 1st floor drift under different damper distributions

致谢：感谢国家留学基金委(CSC)对本文第一作者在美国Houston大学以访问学者身份进行访问期间给予的资助；感谢国家留学基金委(CSC)对本文第二作者在美国Rice 大学以联合培养博士研究生身份进行访问期间给予的资助。

[1] Yao J T P. Concept of structural control[J]. Journal of Structural Division, 1972,98(7):1 567—1 574.

[2] Housner G, Bergman L, Caughey T, et al. Structural control: past, present, and future[J]. Journal of Engineering Mechanics, 1997,123(9):897—971.

[3] 阎维明,周福霖,谭平.土木工程结构振动控制的研究进展[J].世界地震工程,1997,13(2):8—20.

Yan Weiming, Zhou Fulin, Tan Ping. Development of vibration control for civil engineering structures[J]. World Information on Earthquake Engineering, 1997,13(2):8—20.

[4] Symans M, Charney F, Whittaker A, et al. Energy dissipation systems for seismic applications: current practice and recent developments[J]. Journal of Structural Engineering, 2008,134(1):3—21.

[5] Soong T T, Dargush G F. Passive Energy Dissipation Systems in Structural Engineering[M]. Chichester and New York: Wiley, 1997.

[6] Lee D, Taylor D P. Viscous damper development and future trends[J]. The Structural Design of Tall Buildings, 2001,10(5):311—320.

[7] Constantinou M C, Symans M D. Experimental study of seismic response of buildings with supplemental fluid dampers[J]. The Structural Design of Tall Buildings, 1993,2(2):93—192.

[8] Pradlwarter H J, Schu⊇ller G I, Dorka U. Reliability of MDOF-systems with hysteretic devices[J]. Engineering Structures, 1998,20(8):685—691.

[9] Guo A X, Xu Y L, Wu B. Seismic reliability analysis of hysteretic structure with viscoelastic dampers[J]. Engineering Structures, 2002,24(3):373—383.

[10]Güneyisi E M, Altay G. Seismic fragility assessment of effectiveness of viscous dampers in R/C buildings under scenario earthquakes[J]. Structural Safety, 2008,30(5):461—480.

[11]Paola M, Mendola L, Navarra G. Stochastic seismic analysis of structures with nonlinear viscous dampers[J]. Journal of Structural Engineering, 2007,133(10):1 475—1 478.

[12]Di Paola M, Navarra G. Stochastic seismic analysis of MDOF structures with nonlinear viscous dampers[J]. Structural Control and Health Monitoring, 2009,16(3):303—318.

[13]孙广俊,李爱群.安装黏滞阻尼消能支撑结构随机地震反应分析[J].振动与冲击,2009,28(10):117—121.

Sun Guangjun, Li Aiqun. Random earthquake response analysis for an energy dissipation structure adding viscous dampers[J]. Journal of Vibration and Shock, 2009,28(10):117—121.

[14]孙广俊,李爱群.黏滞阻尼减震结构抗震可靠度简化分析[J].防灾减灾工程学报,2010,30(z1):50—57.

Sun Guangjun, Li Aiqun. Simplified analysis of seismic reliability for an energy dissipation structure adding viscous dampers[J]. Journal of Disaster Prevention and Mitigation Engineering, 2010,30(z1):50—57.

[15]孙广俊,李爱群,李鸿晶.基础隔震结构抗震可靠度简化分析方法[J].防灾减灾工程学报,2011,31(5):542—547.

Sun Guangjun, Li Aiqun, Li Hongjing. A simplified analysis method for evaluating seismic reliability of base isolated structures[J]. Journal of Disaster Prevention and Mitigation Engineering, 2011,31(5):542—547.

[16]徐赵东.黏弹性减震控制结构随机状态反应分析[J].振动与冲击,2008,27(1):37—39.

Xu Zhaodong. Random state response analysis for a viscoelastic earthquake-mitigating structure[J]. Journal of Vibration and Shock, 2008,27(1):37—39.

[17]李创第,夏立志,葛新广，等.Maxwell黏滞阻尼器耗能结构的随机地震响应[J].桂林理工大学学报,2011,31(1):61—67.

Li Chuangdi, Xia Lizhi, Ge Xinguang, et al. Structures response in random earthquake for Maxwell viscous dampers[J]. Journal of Guilin University of Technology, 2011,31(1):61—67.

[18]孙香红,王社良,樊燕军.基于体系可靠度的黏滞阻尼布置优化分析[J].武汉理工大学学报,2010,32(9):80—84.

Sun Xianghong, Wang Sheliang, Fan Yanjun. System reliability based topological optimal analysis for viscous dampers[J]. Journal of Wuhan University of Technology, 2010,32(9):80—84.

[19]Li Jie, Chen Jianbing. Stochastic Dynamics of Structures[M]. Singapore: John Wiley & Sons, 2009.

[20]Spanos P D, Kougioumtzoglou I A. Harmonic wavelets based statistical linearization for response evolutionary power spectrum determination[J]. Probabilistic Engineering Mechanics, 2012,27(1):57—68.

[21]孔凡.结构随机动力响应分析及可靠度研究-小波分析与矩演化方法[D].上海:同济大学,2013.

Kong Fan. Research on the stochastic response and reliability analysis of structures via wavelets and moment evolution method[D]. Shanghai, Tongji University, 2013.

[22]Kong Fan, Spanos P D, Li Jie, et al. Response evolutionary power spectrum determination of chain-like MDOF nonlinear structural Systems via harmonic wavelets[J]. International Journal of Non-Linear Mechanics, http://dx.doi.org/10.1016/j.ijnonlinmec.2014.06.002.

[23]Newland D E. Harmonic wavelet analysis[A]. Proceedings of the Royal Society of London. Series A: Mathematical and Physical Sciences， 1993:203—225.

[24]Nason G P, von Sachs R, Kroisandt G. Wavelet processes and adaptive estimation of the evolutionary wavelet spectrum[J]. Journal of the Royal Statistical Society Series B-Statistical Methodology, 2000,62(2):271—295.

[25]丁建华,欧进萍.油缸孔隙式黏滞阻尼器理论与性能试验[J].世界地震工程,2001,17(1):30—35.

Ding Jianhua, Ou Jinping. Theoretical study and performance experiment for cylinder-with-holes viscous damper[J]. World Information on Earthquake Engineering, 2001,17(1):30—35.

[26]周云.黏滞阻尼减震结构设计[M].武汉:武汉理工大学出版社,2006.

Zhou Yun. Design of Energy Dissipation Structure Adding Viscous Dampers[M]. Wuhan: Press of Wuhan University of Technology, 2006.

[27]Liang J W, Chaudhuri S R, Shinozuka M. Simulation of nonostationary stochastic process by spectral representation[J]. Journal of Engineering Mechanics, 2007,133(6):616—627.

[28]孔凡,李杰.非平稳随机过程功率谱密度估计的小波方法[J].振动工程学报,2013,26(3):418—428.

Kong Fan, Li Jie. Power spectrum estimation of non-stationary processes via wavelet[J]. Journal of Vibration Engineering, 2013,26(3):418—428.

[29]Vanmarcke E H. On the distribution of the first-passage time for normal stationary random processes[A]. American Society of Mechanical Engineers, Applied Mechanics Western Conference[C]. University of Hawaii, Honolulu, Hawaii. 1975:1975.

[30]Corotis R B, Vanmarcke E H, Cornell A C. First passage of nonstationary random processes[J]. Journal of the Engineering Mechanics Division, 1972,98(2):401—414.

Seismic reliability of passive controlled MDOF structures equipped with viscous fluid dampers based on Local Stationary Method

SUNXiang-hong1,KONGFan2,LIShu-jin2

(1. School of Civil Engineering, Chang′an University, Xi′an 710061, China;2. School of Civil Engineering & Architecture, Wuhan University of Technology, Wuhan 430070, China)

A novel seismic reliability analysis approach of passive controlled MDOF structural systems subject to full non-stationary earthquake excitations presented via the harmonic wavelet. The structure is equipped with viscous fluid dampers which are widely used in the structural passive controlled structure. Specifically, a Power Spectral Density (PSD) relationship between the excitation and displacement response of controlled structure is firstly obtained, employing the Local Stationary Wavelet representation of non-stationary stochastic process. Next, storey drift reliabilities of distinct storeys are calculated by the response of PSDs and their moments based on the Markovian assumption of the crossing process. Finally, numerical simulations show that different distributions of viscous dampers may lead to distinct storey reliabilities. Pertinent Monte Carlo simulations show the reliability and accuracy of the proposed technique.

stochastic processes; Local Stationary Method; viscous fluid damper; passive control; seismic reliability

2014-01-09；

2014-07-09

中央高校基本科研业务费专项资金资助项目(CHD2011JC115);陕西省自然科学基金资助项目(2006E213)

O324; TB535

A

1004-4523(2015)03-0394-10

10.16385/j.cnki.issn.1004-4523.2015.03.008

孙香红(1974—),女, 副教授。电话：(029)82337250;E-mail:sunxh@chd.edu.cn