基于区间分析的不确定性结构动力学模型修正方法

姜 东， 费庆国， 吴邵庆

(1.南京林业大学机械电子工程学院，江苏 南京 210037；2.江苏省工程力学分析重点实验室, 江苏 南京 210096; 3.东南大学工程力学系, 江苏 南京 210096)

基于区间分析的不确定性结构动力学模型修正方法

姜 东1,2,3， 费庆国2,3， 吴邵庆2,3

(1.南京林业大学机械电子工程学院，江苏 南京 210037；2.江苏省工程力学分析重点实验室, 江苏 南京 210096; 3.东南大学工程力学系, 江苏 南京 210096)

提出了一种基于区间分析的不确定性有限元模型修正方法。在区间参数结构特征值分析理论和确定性有限元模型修正方法基础上，假设不确定性与初始有限元模型误差均较小，采用灵敏度方法推导了待修正参数区间中点值和不确定区间的迭代格式。以三自由度弹簧-质量系统和复合材料板为例，采用拉丁超立方抽样构造仿真试验模态参数样本，开展仿真研究。结果表明，当仿真试验样本能准确反映结构模态参数的区间特性时，方法的收敛精度和效率均较高；修正后计算模态参数能准确反映试验数据的区间特性。所提出方法适用于解决试验样本较少，仅能得到试验模态参数区间的有限元模型修正问题。

模型修正;不确定性； 区间分析； 有限元

引 言

近几十年来，确定性的有限元模型修正技术作为建立精确动力学模型的有效方法已取得长足发展[1]。然而，由于工程问题普遍存在不确定性，迫切需要开展考虑不确定性的结构动力学有限元模型修正方法研究。

工程中的不确定性主要分为以下两类：(1)结构参数的不确定性，例如新型复合材料的物理参数存在较明显不确定性，螺栓、铆钉等连接方式，边界条件难以准确参数化等；(2)试验数据的不确定性，例如高温环境下的模态试验目前在试验方法、测试手段上并不成熟，试验结果离散性较大；模态识别过程中不可避免的存在误差。不确定性在很大程度上影响结构动力学分析结果的可信度。描述参数的不确定主要可分为概率与非概率的方法[2]，概率方法需要丰富的试验数据以得到较准确的统计信息，当试验数据样本较少而不足以准确描述结构的统计特性时，将产生较大的误差[3]。非概率的方法不依赖于数据量的大小。区间分析方法为非概率方法的一种，仅需要参数的上下界即可开展研究，是处理试验数据量较少或某些特殊不确定性问题的有力工具。得益于区间数学理论的提出与发展[4]，以及陈塑寰和邱志平[5-6]、Ben-Haim和Elishakoff[7]等学者的先驱性工作，区间分析方法已成功应用于结构分析的静力学、动力学问题。

在不确定性的有限元模型修正方法研究方面，最初Collins等[8]提出采用统计方法处理了仅考虑噪声引起的试验结果随机性的问题；Mares等[9]采用多元回归模型计算不确定参数的灵敏度矩阵，采用梯度方法计算得到参数的均值和协方差。Hua[10]和Khodaparast[11]分别采用摄动法修正结构参数的均值和标准差，前者需要计算待修正参数的二阶灵敏度矩阵，而后者在不考虑试验数据的不确定性对待修正参数影响的情况下仅计算一阶灵敏度也能得到较准确的结果。Govers和Link[12]将修正问题考虑成试验与计算结果残差最小的优化问题，目标函数包含试验与计算均值的残差以及方差的残差两部分。上述方法均采用概率方法来描述参数或试验数据的不确定性，然后在此基础上进行模型修正，这类方法需要大量的试验数据，增大了工程应用的难度。采用区间分析的不确定性有限元模型修正对试验数据没有严格要求，根据数据的上下限进行修正能够得到相对准确的有限元模型。王登刚和秦仙蓉[13]提出了结构计算模型修正的区间反演方法，将修正问题归结为全局优化问题，并采用遗传算法进行求解。Khodaparast和Mottershead等[14]用克里金模型[15](Kriging Model)来替代有限元模型，在修正过程中采用优化方法来处理区间反问题。然而，替代模型仅能在参数一定取值范围内代替有限元模型,且仅能保证样本处的精度。

考虑试验模态数据以及结构参数的区间不确定性，在区间参数结构特征值分析理论基础上，提出了区间不确定性结构动力学有限元模型修正方法。推导了待修正参数中点值和不确定区间的迭代格式。

1 区间参数结构特征值分析

结构振动特征值问题可表示为

(1)

刚度矩阵K和质量矩阵M均为结构参数的函数，可表示为

(2)

(3)

(4)

对于具有区间参数的结构，结构振动特征值问题的表达式中的刚度矩阵K、质量矩阵M、特征值λ和特征向量u都具有区间性质；特征值的区间可表示为

(5)

(6)

将λ(p)在区间参数中点值附近进行Taylor展开

(7)

其中

(8)

采用区间数学中的区间自然扩张理论[4]，由式(7)可得

(9)

通过区间运算，可得到特征值区间的上界

(10)

和下界

(11)

其中，特征值对参数的一阶导数

(12)

2 不确定性模型修正方法

在确定性方法的基础上推导区间不确定性结构有限元模型修正方法的迭代格式。确定性的有限元模型修正可归结为优化问题

(13)

目标函数J(p)定义为在结构待修正参数p∈RN的合理取值范围p1≤p≤p2内，试验与计算模态参数的加权残差取极小值。ε为模态参数的残差，zm,za(p)∈Rn分别为试验与计算的模态参数；p∈RN为结构待修正参数的N维向量；加权矩阵W为反映各模态参数残差相对权重的对角阵。设定待修正参数的初值，采用灵敏度分析的方法迭代求解优化问题，确定性的有限元模型修正第j个迭代步的问题描述为

(14)

为了表述方便，先不考虑各阶模态参数残差的相对权重，修正问题转化为

(15)

其中Sj=∂zj/∂pj表示模态参数对待修正参数的灵敏度矩阵，可根据式(12)计算得到。

为了考虑试验数据、结构参数的区间不确定性，将式(15)中的变量采用区间分析的方法表示为

(16)

(17)

(18)

将式(16)代入式(15)，可得

(19)

采用摄动法，将式(19)中的关于Δ的零阶项和一阶项分离，并忽略二阶项可得

(20)

(21)

分别求解式(20)与(21)，得到待修正参数中点值与不确定性区间的迭代格式

(22)

(23)

其中

(24)

若考虑加权，且计算模态参数对待修正参数的加权灵敏度矩阵病态，应采用求解不适定问题的正则化方法[16]，则

(25)

式中W1为反映各模态参数残差相对权重的对角加权矩阵；W2=αI，其中α为正则化参数，通过作L-curve图可求得α的值。

基于区间分析的不确定性结构动力学有限元模型修正方法实现步骤如下：

(7)满足精度，参数收敛，则迭代终止。

3 仿真算例研究

以三自由度弹簧-质量系统和复合材料板为例，采用拉丁超立方体抽样(LatinHypercubeSampling,LHS)[17]，按照参数的真实值构造样本，代入有限元模型中计算得到仿真试验样本，开展仿真研究来验证方法的可行性。

3.1 算例一 三自由度系统

如图1所示为三自由度弹簧-质量系统[14]。在此模型中，确定性的参数为：

m1=m2=m3=1.0 kg,k3=k4=1.0 N/m,k6=3.0 N/m。

假设其他不确定的弹簧弹性系数取值区间为：

k1=[0.8 1.2] N/m,k2=[0.8 1.2] N/m,k5=[0.8 1.2] N/m。

图1 三自由度弹簧-质量系统Fig.1 Three degrees of freedom spring-mass system

图2 待修正参数区间的迭代收敛曲线 (10 samples)Fig.2 Convergence of the interval of updating parameters

以均匀分布的拉丁超立方体抽样分别构造10个和1 000个试验样本，针对三自由度弹簧-质量模型开展基于区间分析的不确定性模型修正方法仿真研究。由于试验的模态参数通过仿真得到，试验数据不受其他因素影响，取加权矩阵W1=I；迭代过程中修正问题的线性方程组性态良好，未出现病态，取正则化参数α=0。

假设不确定的待修正参数初始值为：

k1=[1.5 2.5] N/m,k2=[1.5 2.5] N/m,k5=[1.5 2.5] N/m。

如图2所示为待修正参数区间的迭代收敛曲线(10 samples)，对于三自由度弹簧-质量系统，区间参数的中点值与区间参数宽度均经过8次迭代，收敛到真实值附近；试验样本数量为1 000时，收敛曲线同样能快速收敛。对不同数量试验样本情况下的修正精度进行了比较分析，图3和4所示为修正前后参数区间的比较，表1和2所示为修正前后的参数区间误差。10个样本情况的修正误差大于样本数为1 000的情况，表明样本数量越多，试验样本的区间越准确，则修正结果更精确。

图3 修正前后参数区间的比较 (10 samples)Fig.3 Comparison between the initial and updated interval of parameters (10 samples)

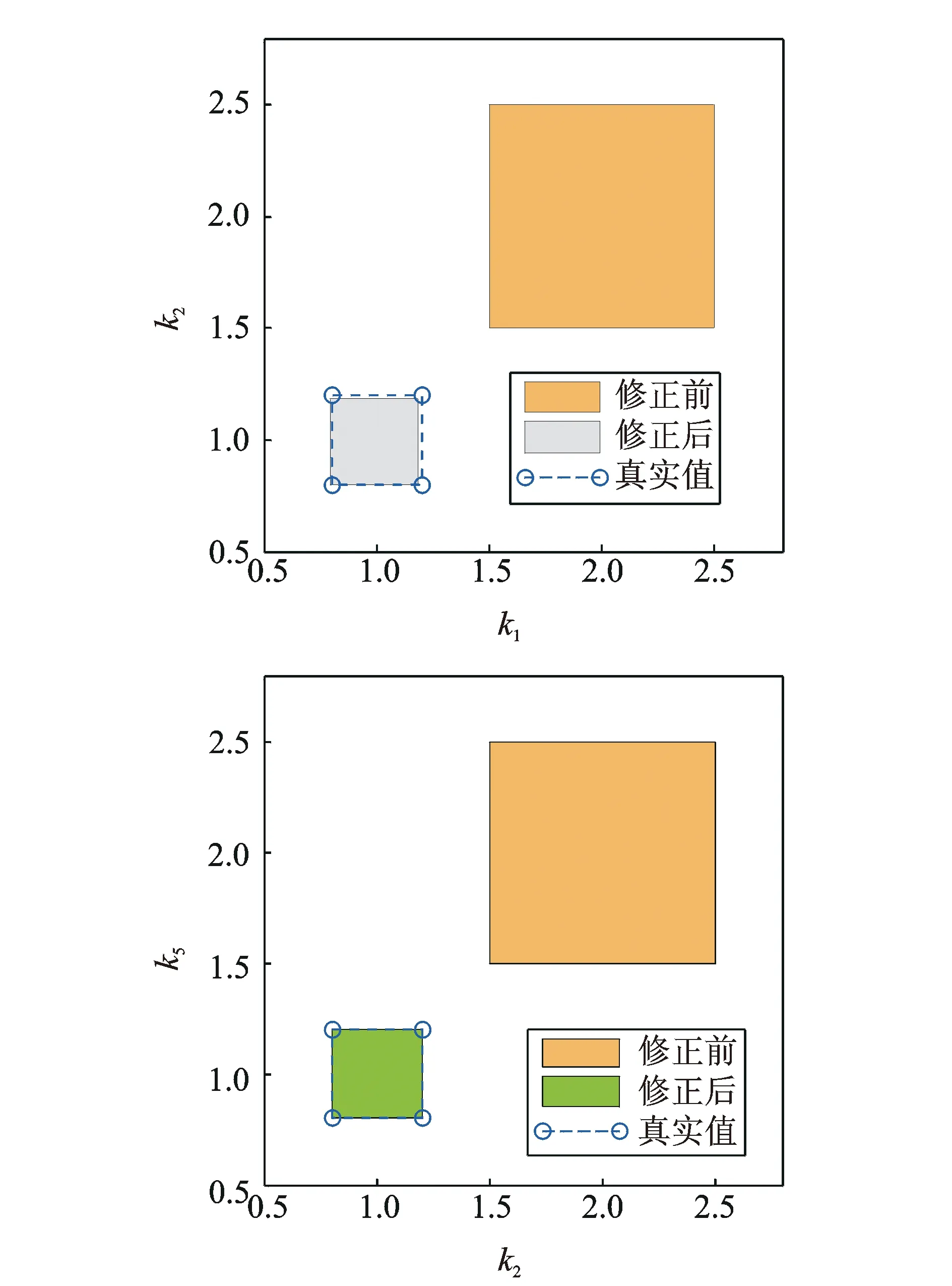
图4 修正前后参数区间的比较(1 000 samples)Fig.4 Comparison between the initial and updated interval of parameters (1 000 samples)

图5 修正前后计算模态参数与试验数据比较的散点图(1 000次计算)Fig.5 Scatter plot of the comparison between the numerical and experimental modal data (1 000 samples)

根据修正前后待修正参数的区间，采用均匀分布的拉丁超立方体抽样构造参数的随机样本，代入确定性的有限元模型中计算修正前后的模态参数，如图5为修正前后计算模态参数与试验数据比较的散点图(计算1 000次)，从图中可以看出，修正之后模型的计算模态数据与10个试验样本吻合良好，能够准确反映试验结果。

表1 修正前后的参数区间误差比较(10 samples)

Tab.1 Comparison of errors between initial and updated parameters (10 samples)

系统参数/(N·m-1)真实值修正后中点值区间半径中点值误差/%区间半径误差/%k11．00．21．0282．80．1981-0．95k21．00．20．9891．10．197-1．5k51．00．20．9920．80．195-2．5

表2 修正前后的参数区间误差比较(1 000 samples)

Tab.2 Comparison of errors between initial and updated parameters (1 000 samples)

系统参数/(N·m-1)真实值修正后中点值区间半径中点值误差/%区间半径误差/%k11．00．20．999-0．10．1985-0．75k21．00．21．002-0．20．198-1．0k51．00．21．0010．10．1985-0．75

3.2 算例二复合材料板

以几何尺寸为300 mm×300 mm×3 mm，弹性参数如表3所示的复合材料板为例，进一步开展考虑区间不确定性的有限元模型修正方法仿真研究。通过灵敏度分析选取对复合材料板动态特性影响最大的3个参数E11，E22和G12为待修正参数。

假设复合材料弹性参数中E11，E22和G12的真实区间分别为：

E11=114.16+[-11.416 11.416] GPa

E22=124.0+[-12.4 12.4] GPa

G12=36.24+[-3.624 3.624] GPa

表3 复合材料弹性参数

根据参数的真实区间，采用拉丁超立方体采样获得复合材料板的试验模态参数区间。假设待修正参数的初始值：

E11=91.328+[-17.124 17.124] GPa

E22=99.208+[-18.6 18.6] GPa

G12=43.488+[-5.436 5.436] GPa

即材料的弹性模量E11，E22区间中点值被低估了20%，剪切模量G12区间中点值被高估了20%；3个参数的区间半径初始误差均为+50%。

采用均匀分布的拉丁超立方体抽样根据不确定弹性参数的真实区间构造1 000个随机样本，代入有限元模型中计算得到仿真的试验模态参数样本，由此得到试验模态参数的区间，作为不确定性参数修正研究中的模态参数目标值。

图6 待修正区间参数误差迭代收敛曲线(1 000 samples)Fig.6 Convergence of the errors of interval updating parameters

如图6所示为区间参数中点值与区间半径误差迭代收敛曲线(1 000 samples)，从图中可以看出，弹性参数的区间中点值、区间半径在迭代到第六个迭代步时收敛，收敛后误差均较小。表4所示为修正后弹性参数区间误差，修正后弹性参数区间中点值的误差绝对值由20%下降到1%以下，区间半径误差不超过5%。为了更加直观地比较修正后计算频率与试验频率，图7中给出修正前后计算频率区间与试验模态参数样本比较，可以看出修正后结果与计算结果吻合良好。

表4 修正后弹性参数区间误差(1 000 samples)

Tab.4 Errors of the updated elastic parameters with interval uncertainty (1 000 samples)

系统参数/(N·m-1)真实值修正后中点值区间半径中点值误差/%区间半径误差/%E11114．1611．416113．28-0．7710．904-4．49E22124．012．40123．35-0．5211．80-4．84G1236．243．62436．260．053．447-4．87

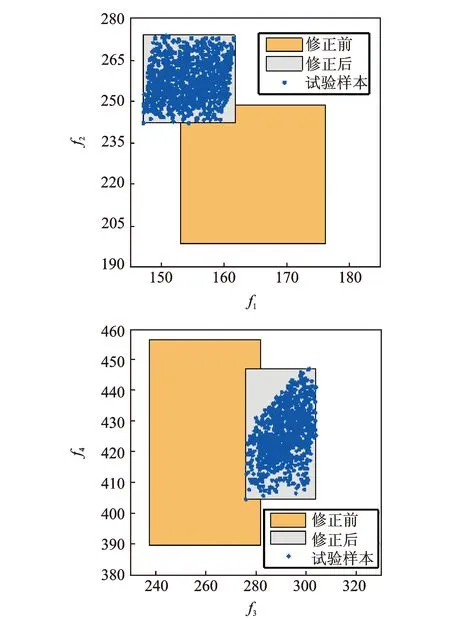
图7 修正前后计算模态参数区间与试验模态参数样本的比较 (1 000 samples)Fig.7 Interval comparison between the numerical and experimental modal data after updating

4 结 论

根据区间扩张理论计算模型修正过程中模态参数和灵敏度矩阵的不确定性区间，推导了待修正参数区间中点值和不确定区间的迭代格式，提出一种试验模态数据以及结构参数存在区间不确定性的模型修正方法。由于理论推导过程中采用了区间扩张理论与灵敏度方法，本文方法仅用于不确定性和初始有限元模型误差均较小的情况，收敛效率较高。通过三自由度弹簧-质量系统及复合材料板的仿真研究表明，样本区间的准确性是影响修正结果的重要因素；对于所采用的算例，区间参数的中点值与区间半径均能快速的收敛到真实值。根据修正后参数的区间构造随机样本，带入确定性的有限元模型中进行计算，修正之后模型的计算模态数据与试验样本吻合良好，能够准确反映试验数据的区间特性。

[1] Mottershead J E, Link M, Friswell M I. The sensitivity method in finite element model updating: A tutorial[J]. Mechanical Systems and Signal Processing,2011, 25:2 275—2 296.

[2] Moens D, Vandepitte D. A survey of non-probabilistic uncertainty treatment in finite element analysis[J]. Computer Methods in Applied Mechanics and Engineering, 2005, 194(12):1 527—1 555.

[3] Ferson S, Ginzburg L R. Different methods are needed to propagate ignorance and variability[J]. Reliability Engineering and System Safety,1996, 54(2): 133—144.

[4] Moore R E, Kearfott R B, Cloud M J. Introduction to Interval Analysis[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2009.

[5] Chen S H, Qiu Z P, Song D T. A new method for computing the upper and lower bounds on frequencies of structures with interval parameters[J]. Mechanics Research Communications, 1994, 21(6): 583—592.

[6] Qiu Z P, Chen S H, Elishakoff I. Natural frequencies of structures with uncertain but nonrandom parameters[J]. Journal of Optimization Theory and Applications, 1995, 86(3): 669—683.

[7] Ben-Haim Y, Elishakoff I. Convex Models of Uncertainty in Applied Mechanics [M]. Amsterdam:Elsevier, 1990.

[8] Collins J D, Hart G C, Hasselman T K, et al. Statistical identification of structures [J]. AIAA Journal, 1974, 12 (2): 185—190.

[9] Mares C, Mottershead J E, Friswell M I. Stochastic model updating: part 1—Theory and simulated example [J]. Mechanical Systems and Signal Processing, 2006, 20(7):1 674—1 695.

[10]Khodaparast H H, Mottershead J E, Friswell M I. Perturbation methods for the estimation of parameter variability in stochastic model updating[J]. Mechanical Systems and Signal Processing, 2008,22(8): 1 751—1 773.

[11]Hua X G, Ni Y Q, Chen Z Q, et al. An improved perturbation method for stochastic finite element model updating [J]. International Journal for Numerical Methods in Engineering, 2008, 73(13):1 845—1 864.

[12]Govers Y, Link M. Stochastic model updating: covariance matrix adjustment from uncertain experimental modal data [J]. Mechanical Systems and Signal Processing, 2010,24 (3): 696—706.

[13]王登刚, 秦仙蓉. 结构计算模型修正的区间反演方法[J]. 振动工程学报, 2004,17 (2): 205—209.

WANG Deng-gang, Qin Xianrong. Interval method for computational model updating of dynamic structures [J]. Journal of Vibration Engineering, 2004, 17 (2): 205—209.

[14]Khodaparast H H, Mottershead J E, Badcock K J. Interval model updating with irreducible uncertainty using the Kriging predictor[J]. Mechanical Systems and Signal Processing, 2011,25(4):1 204—1 226.

[15]Simpson T W, Mauery T W, Korte J J, et al. Kriging models for global approximation in simulation-based multidisciplinary design optimization[J]. AIAA Journal, 2001, 39(12): 2 233—2 241.

[16]Ahmadian H, Mottershead J E, Friswell M I. Regularization methods for finite element model updating[J]. Mechanical Systems and Signal Processing, 1998, 12(1): 47—64.

[17]Helton J C, Davis F J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems[J]. Reliability Engineering and System Safety, 2003,81(1): 23—69.

Updating of structural dynamics model with uncertainty based on interval analysis

JIANGDong1, 2,3,FEIQing-guo2,3,WUShao-qing2,3

(1.College of Mechanical and Electronic Engineering, Nanjing Forestry University,Nanjing 210037, China;2. Jiangsu Key Laboratory of Engineering Mechanics, Nanjing 210096, China;3. Department of Engineering Mechanics, Southeast University, Nanjing 210096, China)

A finite element model updating method in structural dynamics considering the effects of uncertainty is proposed using interval analysis. Based on the theory of eigen-frequency analysis of structures with interval parameters and the deterministic finite element model updating technologies, an interval model updating formulation are developed by applying the sensitivity method, under the assumption that the variability in measurements and structural parameters as well as the error in the initial finite element model are small. In the iterative formulation, each variable is presented in an interval form which consists of an interval mid-point and an interval radius. Simulation study is conducted by employing a three degrees of freedom mass-spring system and a composite panel, the simulated experimental samples are generated by adopting Latin Hypercube sampling methods. Results show that when the testing samples can accurately reflect the interval characteristics of the experimental modal data, the high convergence accuracy and high efficiency can both be achieved. The presented method provides a solution to the problem that the measured sample is small in finite element model updating of structures with uncertainties.

model updating; uncertainty; interval analysis; finite element method

2013-11-19；

2014-04-18

国家自然科学基金资助项目(10902024)；教育部新世纪优秀人才支持计划(NCEF-11-0086)；江苏省自然科学基金资助项目(BK2010397)；江苏高校优势学科建设工程资助项目(1105007001)

O325； TB123

A

1004-4523(2015)03-0352-07

10.16385/j.cnki.issn.1004-4523.2015.03.003

姜东(1985—), 男, 博士,讲师。 E-mail: jiangdonal@gmail.com