RLC并联谐振电路的实验研究
刘小艳,金 平,杨 毅
(清华大学 电子工程系,北京 100084)
RLC并联谐振电路的实验研究
刘小艳,金 平,杨 毅
(清华大学 电子工程系,北京 100084)
RLC并联谐振电路在实际应用中非常普遍,而目前高校电子电路实验中关于RLC并联谐振电路的实验研究却很少。文中提出利用晶体管共射极放大电路构造一个压控电流源作为RLC并联谐振电路的电流源激励的方法,对RLC并联谐振电路的阻抗特性及其应用等进行研究。实验结果表明,该方法完全可行,适用于高校电子电路实验教学。
RLC并联谐振电路;晶体管共射极放大电路;电流源;阻抗特性
RLC并联谐振电路在电流源激励下,其输出电压具有带通选频特性,而晶体管放大器工作在有源区时的电路模型就是受控电流源。这使得RLC并联谐振电路在实际应用中比RLC串联谐振电路更为广泛[1]。
目前,高校电子电路实验教学中大多开展了RLC串联谐振电路的实验,而关于RLC并联谐振电路的实验研究却很少,或者只是采用EDA工具进行仿真实验[2-7]。原因可能在于大多数实验室没有合适的RLC并联谐振电路激励源。本文提出利用晶体管共射极放大电路构造一个压控电流源作为RLC并联谐振电路的电流源激励的方法,对RLC并联谐振电路的阻抗特性及其应用等进行研究,并将其应用在电子电路与系统基础实验教学中,取得了很好的教学效果。
1 原理与实验电路
研究RLC并联谐振的实验电路如图1所示。图1中虚线方框内的部分为晶体管T和阻容元件组成的典型共射极放大电路,RLC并联谐振电路是其集电极负载。设置合适的静态工作点使晶体管T工作在放大状态,射极电阻RE2是电流取样电阻,引入了较深的电流串联负反馈,使得从集电极进去的输出电阻很高,所以晶体管的集电极输出电流ic便可看成是受输入电压vi控制的交流电流源。图1的交流等效电路如图2 所示(图中iS=-ic)。晶体管集电极电流ic即为RLC并联谐振电路的激励电流iS。图2中的Rp为并联谐振电路的等效电阻,它包括外加电阻R和电抗元件的固有损耗电阻。

图1 RLC并联谐振实验电路

图2 RLC并联谐振实验电路的交流等效电路
由图2得到,RLC并联电路的阻抗Zp(jw)为[8-9]:

(1)

(2)
由式(1)可以得到,RLC并联电路阻抗的模和相角随频率变化的关系分别为:

(3)

(4)

式(1)中,当w与w0相差很小时,即假设w=w0+Δw,则有:

(5)
一般fH和fL均与f0相差很小,假设fH=f0+Δf1,当频率为上限截止频率fH时,式(1)中分母的虚部为1;假设fL=f0+Δf2,当频率为上限截止频率fL时,式(1)中分母的虚部为-1。则根据式(5)有:
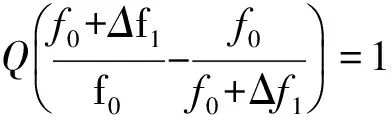

再根据
BW=fH-fL=(f0+Δf1)-(f0+Δf2)=Δf1-Δf2
得到:

(6)
下面分析通过图1的实验电路如何测得RLC并联电路的阻抗特性。当RLC并联电路谐振时,输出电压vo与激励电流iS的相位相同,与晶体管集电极电流iC相位相反。假设满足(β+1)RE2≫rbe,rbe为晶体管基极与发射极之间的动态电阻,则晶体管射极信号电压ve近似等于输入电压vi,即vi≈ve=ieRE2≈icRE2。这说明,调节vi即可改变ic(压控电流源),同时,电路的激励电流ic可通过测量射极电压ve间接获得,即:

(7)
当RLC并联电路谐振时,输出电压vo与射极电压ve两者相位刚好相反。实验中RLC并联谐振电路的阻抗可以利用以下公式计算得到:

(8)
由式(8)得到,阻抗的模和相角分别为:
(9)
φ(w)=φ0-φe+π
(10)
由此可见,RLC并联谐振电路的阻抗可以通过测量输出电压vo与射极电压ve间接得到。
2 实验结果与分析
2.1 实验结果
实验电路如图1所示,其中直流电源电压VCC为+12 V。
要使晶体管共射极放大电路构造的受控电流源接近理想电流源,就要使受控电流源的内阻接近无穷大,除了增加射极负反馈电阻RE2来增加受控电流源内阻外,还要尽量增大晶体管的rce。为了使rce足够大,晶体管的静态工作点ICQ就不能太大。
这里需要说明的是,利用仪器仪表测得的实验数据和计算得到的数据均取3位有效数字。
用UT39A型数字万用表测得RE1为1.000 kΩ,RE2为0.506 kΩ,R为9.980 kΩ。调节电位器RW,同时用UT39A型数字万用表测量RE1两端的电压,当显示电压值约为1.000 V时,停止调节电位器RW,即此时晶体管T的ICQ≈1.000 mA。
输入信号vi为EE1642C1型函数信号发生器产生的正弦交流信号。调整该函数信号发生器改变输入信号频率,同时用DSO-X 2012A型数字示波器观察输出电压vo与射极电压ve的波形,改变输入信号频率的同时保证射极电压ve的峰值保持在30.0 mV。输入信号频率点选择的一般原则为:在谐振频率的两侧对称取点;离谐振频率点近处取点较多,离谐振频率点远处取点较少。用DSO-X 2012A型数字示波器测得不同频率的输出信号峰峰值(vopp)和ve与vo的相位差(φe-φ0),如表1所示。

表1 实验数据

续表1
2.2 分析RLC并联谐振电路的阻抗特性(频率特性)及主要特性参数
由表1的实验数据可知,该RLC并联谐振电路的谐振频率fo=425 kHz,谐振时输出电压峰峰值为210 mV,根据式(9)计算得到此时并联谐振电路的阻抗大小为3.54 kΩ,即谐振电阻大小为3.54 kΩ。同时,由表1可以得到该RLC并联谐振电路的上限截止频率fH=441 kHz,下限截止频率fL=409 kHz,计算得到带宽BW=fH-fL=32.0 kHz,品质因数Q≈fo/BW≈13.3。

同样,由表1的频率和φe-φo数据,根据式(10)计算得到阻抗的相角φ(实验数据)如表2的第四列,画出阻抗的相角φ随频率f变化的实验曲线如图4中的空心圆圈标注的曲线所示。根据阻抗的相角的理论公式(4),式中的Rp=3.54 kΩ、L=92.2 μH、C=1.55 nF,计算得到阻抗的相角φ(理论计算数据)如表2的第五列,画出相应的理论曲线如图4中的实心圆圈标注的曲线所示。

表2 阻抗的模的实验数据和理论数据

续表2
由图3和图4可以看出,阻抗的模和相角随频率变化的实验曲线和理论计算曲线基本吻合,但也存在一定的偏差。

图3 阻抗的模随频率变化的曲线

图4 阻抗的相角随频率变化的曲线
出现偏差的原因主要有以下几点:
1)晶体管共射极放大电路构造的电流源并非理想电流源,且RLC并联谐振电路的激励电流其实是晶体管共射极放大电路的集电极电流,而计算时认为此激励电流是晶体管共射极放大电路的射极电流。
2)Rp为并联谐振电路的等效电阻,它包含了电抗元件的固有损耗电阻,会随着工作频率变化而变化,而计算时固定Rp为电路工作在谐振频率时的值。
3)电感L与电容C的值会随着工作频率变化而变化,而理论计算时固定电感L与电容C为工作在谐振频率时测得的值。
4)实验测量误差和计算中取3位有限的有效数字带来的误差等。
另外,图3所示阻抗的模随频率变化的曲线并不关于谐振频率两侧对称,谐振频率左侧的曲线较右侧的曲线陡峭,这可从阻抗的模的理论计算公式来加以分析[5]。假定Rp在实验测量的频率变化范围内保持不变(或变化可忽略),在谐振频率f0的两侧取阻抗相同的两点,左侧点对应的频率为f1,右侧点对应的频率为f2,则由式(3)容易得到:

化简后得到:
(11)
令f1= f0-Δf1,f2= f0+Δf2,代入式 (11) 化简后得到:

(12)
由式 (12) 可见,谐振频率两侧阻抗的模相等的两个点中,左侧点离谐振频率比右侧点离谐振频率要近,故谐振频率左侧的曲线较右侧的曲线陡峭。若电路的谐振频率较高,f0>>Δf1,则Δf1≈Δf2,谐振曲线的对称性不明显。
图4所示阻抗的相角随频率变化的曲线也不关于谐振频率点中心对称,谐振频率左侧的曲线较右侧的曲线陡峭,同样可以从阻抗的相角的理论计算公式来加以分析,方法与上述分析阻抗的模随频率变化的方法相同,不再赘述。
以上实验结果和理论分析说明,利用晶体管共射极放大电路构造一个电流源激励RLC并联谐振电路的实验方法完全可行。
另外,由表1所示的实验数据可以看出,RLC并联电路具有很好的带通选频特性,将其作为选频网络可应用在小信号放大器、A类、B类、C类大信号放大器中。
3 结束语
综上所述,利用晶体管共射极放大电路构造一个压控电流源激励RLC并联谐振电路的方法,以此开展RLC并联谐振电路的阻抗特性及其应用等研究,实验现象明显,且符合理论分析。这种方法很好地弥补了实验室没有合适的RLC并联谐振电路激励源的不足,非常适用于高校电子电路实验教学,一方面有利于学生深刻掌握RLC并联谐振电路的基本特性及其应用,另一方面可以引导学生用理论计算与实验验证相结合的方法进行分析。这样既可以扩展知识又可以将RLC并联谐振电路的学习引向深入。
[1]于歆杰,朱桂萍,陆文娟. 电路原理[M]. 北京: 清华大学出版社, 2007:300-303.
[2] 楼珍丽,干于. EDA技术在电路实验课程中的应用[J]. 实验科学与技术, 2008, 6(4):12-13.
[3] 郑桂容,孟桂菊. RLC串联电路谐振特性实验方法的改进[J]. 黄冈师范学院学报, 2009, 29(3):30-32.
[4] 朱华光,朱玮玮. RLC串联谐振电路的实验研究[J]. 现代电子技术, 2010(21):199-202.
[5] 陆申龙,曹正东. RLC串联谐振教学实验的研究[J]. 物理实验, 1995, 16(3):109-111.
[6] 吴凌燕. 基于Mulitisim11的串联谐振电路特性研究[J]. 应用天地, 2011, 30(8):84-86.
[7] 姚缨英. 电路实验教程[M]. 2版.北京: 高等教育出版社, 2011.
[8] 董在望,陈雅琴,雷有华,等. 通信电路原理[M].2版. 北京: 高等教育出版社, 2002:32-35.
[9] 叶爱琴,王玉莲. 几种RLC谐振电路的特性对比[J]. 安徽农业技术师范学院学报,2000,14(2):68-70.
古往今来杰出的科学家、艺术家、文学家无不都是靠自己学习,才能有所发明,有所创造,谁能教莎士比亚成为莎士比亚?谁能教爱因斯坦发现解释宇宙的根本原理?谁能教鲁迅先生刻画出阿Q的形象?自己的学习和创造是前进的一种动力。
——许国璋
Experiment Research of RLC Parallel Resonant Circuit
LIU Xiaoyan, JIN Ping, YANG Yi
(Department of Electronic Engineering, Tsinghua University, Beijing 100084, China)
RLCparallel resonant circuit is very common in actual applications, but the experimental study about it is very little in the university course of electronic circuit experiment at present. This paper proposes a method of using common emitter transistor amplifier circuit to construct a voltage-controlled current source as the current source excitation ofRLCparallel resonant circuit. On this basis the impedance characteristics and application ofRLCparallel resonant circuit are researched. The experimental results show that this method is completely feasible and very ideal for electronic circuits experiment teaching in university.
RLCparallel resonant circuit; common emitter transistor amplifier circuit; current source; impedance characteristics
2014-03-26;修改日期: 2014-04-27
刘小艳(1983-),女,硕士,工程师,主要从事电子电路方面的实验教学和科研工作。
TN710;G642.426
A
10.3969/j.issn.1672-4550.2015.02.006

