自升式平台悬臂梁结构屈服强度分析

冯 琦， 陈 艳， 任康旭， 郭培军

(1. 宏华海洋油气装备(江苏)有限公司，江苏 南通226256； 2. 上海船舶工艺研究所，上海 200032)

自升式平台悬臂梁结构屈服强度分析

冯 琦1， 陈 艳1， 任康旭2， 郭培军1

(1. 宏华海洋油气装备(江苏)有限公司，江苏 南通226256； 2. 上海船舶工艺研究所，上海 200032)

该文提出了一种手工总纵强度校核方法，并依据ABS规范，使用ANSYS软件校核了自升式平台悬臂梁在不同悬伸和不同钻台位置时的结构屈服强度。并采用非线性弹簧模拟具有非线性力学性能的高分子材料，通过多次迭代计算悬臂梁在固定载荷、钻井可变载荷作用下的总纵弯矩和结构应力。结果表明，该文提出的方法可以快速有效的进行悬臂梁结构强度分析，对悬臂梁的设计也有一定的指导作用。

自升式平台；悬臂梁；总纵强度；非线性

0 前言

自升式平台主要工作在水深为10 m～150 m的水域，由于工作时主船体可以升高至水面以上，而且桩腿所承受的水动力比较小，故其具有良好的稳定性，应用十分广泛。近年来, 自升式平台的设计理念已经从传统的纯勘探钻井发展到勘探和开发钻井并举。为此,新建和待建的自升式平台几乎均设计成悬臂梁式钻井平台,因此研究悬臂梁的总体强度具有十分重要的意义。

1 平台简介

图1 悬臂梁悬伸和钻台偏移

此次分析是基于宏华海洋油气装备(江苏)有限公司设计的122 m自升式平台，其主尺度见表1。悬臂梁可通过棘爪爬行装置和滑移系统沿船艏、船尾方向纵向滑移，主船体上的纵向滑移基座是由横向楔子结构、纵向销子结构、垂向支撑结构和艉部滚轮支撑结构组成。悬臂梁上设置有滑道以支撑钻台，并允许钻台在悬臂梁上进行左舷、右舷方向的横向滑移，悬臂梁悬伸和钻台偏移如图1所示。

表1 自升式平台的主要参数

2 分析方法

悬臂梁作业时主要是通过平台尾部的滚轮提供向上的支撑力，如图2所示，通过船中的下拉夹具限制悬臂梁向上的运动，如图3所示。

图2 滚轮 图3 下拉限位夹具

悬臂梁可以简化为端部和中间简支的外伸梁，此模型在受到单位端部集中力和均布力时，其受力模型如图4、图5所示。

图4 外伸梁受集中载荷剪力弯矩图 图5 外伸梁受均布载荷剪力弯矩图

根据图4和图5可知，最大弯矩和最大剪力均出现在滚轮的位置，滚轮对应的悬臂梁结构的总纵弯矩起主导作用。

3 总纵弯矩分析

3.1 自重

悬臂梁的自重主要包括悬臂梁的净重和钻台的净重。臂梁的净重包括结构、舾装、管线、设备及其内部流体等共重1 442 t，净重采取分段均布载荷的形式，载荷形式分别作用于悬臂梁的2道纵壁；钻台的净重包括井架、钻台结构、舾装、管线、设备及其内部流体等的重量，根据重量重心的分布，可以换算到悬臂梁上四个钻台的支撑点处。具体载荷值及所产生的弯矩见表2、表3。

表2 悬伸22.86 m，钻台偏移4.572 m时的自重分布和对应弯矩

表3 悬伸13.716 m，钻台偏移4.572 m时的自重分布和对应弯矩

3.2 可变载荷

钻台的可变载荷由钩载、立根载荷、钻盘载荷和套管张力载荷依据钻台的具体位置确定，具体值见表4。根据载荷的大小及重心位置可求出不同工况下所对应的悬臂梁的总纵弯矩。

运用大数据技术，可确保审计证据的获取、审计报告的编写、审计结论的得出都是基于真实、完整、可靠的海量数据，通过深度挖掘数据反映的经济活动合理性与合法性，让数据“发声”，可以有效的减少审计人员的主观判断，并且通过概率比率分析等数据辅助决策，可以提高审计人员职业判断的准确性，从而提高审计结论的客观性与独立性。此外，大数据时代的全样本审计，能够降低甚至消灭抽样风险，帮助审计人员获得充分、恰当的审计证据，对被审计单位的运营情况进行全面审查与整体评价，进一步增强审计结果的客观性与真实性。

表4 同悬伸和钻井平台位置的可变载荷

上述的固定载荷和可变载荷在距钻井中心9 m滑移壁上的载荷分布如图6所示，其中q1至q6为均布载荷，F1、F2和F3为集中载荷。

图6 单侧9 m舱壁载荷分布情况

3.3 最大许用总纵弯矩

悬臂梁的总纵弯矩是由距钻井中心9 m两道滑移壁来承担，此舱壁沿纵向的剖面形状有所变化，不同位置的剖面形状、属性和所计算的许用弯矩见表5、表6。其中剖面1、剖面2、剖面3和剖面4距钻井中心的纵向距离范围分别是-6 100 mm～6 100 mm、6 100 mm～12 200 mm、12 200 mm～36 600 mm和36 600 mm～46 900 mm。

表5 剖面1和剖面2的属性和剖面形状

表6 剖面3和剖面4的属性和剖面形状

3.4 不同工况的总纵弯矩

综合悬臂梁在不同悬伸和不同钻井位置的固定载荷和可变载荷，可得出其所对应的悬臂梁在不同剖面的总纵弯矩。钻井平台处于不同位置时所对应各种悬伸的总纵弯矩和许用弯矩的比较如图7～图10所示。由图7～图10可知，所有工况下各个剖面的总纵弯矩都小于所对应的许用弯矩。

图7 钻台在中心时各的弯矩比较 图8 钻台向左舷偏移1.2 m时的弯矩比较

图9 向左舷偏移2.7 m时的弯矩比较 图10 向左舷偏移4.6 m时的弯矩比较

4 屈服强度详细分析

在保证悬臂梁的总纵强度情况下，还要考察悬臂梁的整体应力分布、应力集中部位的应力分布，比如滚轮和下拉夹具所在位置，特别是在滚轮位置，在艉封板处应力集中非常严重，为缓解局部的应力集中问题，除了要仔细校核滚轮的数量和面积是否足够，还要计入滚轮的下方高分子材料变形对强度的影响。

图11 有限元模型

4.1 有限元模型的建立

图12 高分子材料载荷变形特性

悬臂梁结构的有限元模型考虑了钻台的布置、滑移装置、主体、关节吊底座局部加强以及钻台支撑处局部加强等。

有限元模型的板和梁系的腹板采用壳体单元shell163建立，梁系的面板和加强筋采用梁单元beam188建立，滑板采用实体单元solid45建立，载荷的传递采用约束单元建立，具体模型如图11所示，边界条件采用弹簧单元combin39建立。

4.2 高分子材料的模拟

正常作业状态下悬臂梁的所有载荷通过四套滑移系统传递到主船体上。因此，对于悬臂梁与船艏接触区域，采用线性弹簧单元对悬臂梁轨道与滑移系统接触区域建立边界条件。对于悬臂梁与船艉接触区域，滚轮下方铺设了一层高分子材料，高分子材料的性能如图12所示，通过高分子材料变形可以有效缓解该区域的应力集中问题，为了精确的模拟高分子材料的作用，采用非线性弹簧模拟具有非线性力学性能的高分子材料来建立边界条件，在ANSYS 中模拟的弹簧特性如图13所示，加载在模型中的弹簧如图14所示。

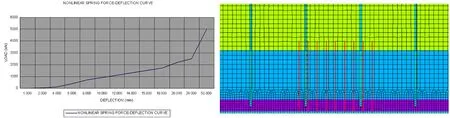
图13 模拟的弹簧变形特性 图14 模型边界条件

4.3 载荷工况确定和求解

假设操作状态时的静态载荷决定着悬臂梁的结构强度。由于悬臂梁外伸出船体长度的不同，施加在悬臂梁上的最大可变载荷也不同。如下所示为两种极端外伸工况需要考虑：外伸75英尺 (22.86 m, 最大外伸长度对应最大弯矩工况)；外伸50英尺(15.24 m, 最大可变载荷对应最大剪力工况)；在ANSYS中主要校核以下四种极限位置组合工况：悬伸22.86 m，钻井平台处于中线位置，最大可变载荷为1 180 t；悬伸22.86 m，钻井平台向右舷偏移4.57 m，最大可变载荷为495 t；悬伸13.716 m，钻井平台处于中线位置，最大可变载荷为1 180 t；悬伸13.716 m，钻井平台向右舷偏移4.57 m，最大可变载荷为1 180 t。

其他载荷和总纵弯矩校核中的载荷相同。求解的结果分别如图15～图21所示，应力值均在许用应力范围之内。

图15 工况1的von mises 应力云图 图16 工况2的von mises 应力云图

图17 工况3的von mises 应力云图 图18 工况4的von mises 应力云图

图19 最大正应力σX 图20 最大正应力σZ 图21 最大剪应力τXZ

5 结论

(1) 通过手工的总纵强度校核和有限元分析，悬臂梁在长度方向的最大正应力均出现在滚轮支撑对应的位置，所以在悬臂梁的设计过程中，悬臂梁作业时滚轮对应的悬伸长度区域内要进行加强。

(2) 非线性高分子材料的应用，可以有效缓解应力集中，约束区域的应力分布趋向合理。

(3) 悬伸长度和可变载荷对悬臂梁的强度起到了决定性作用。

(4) 钻台的横向移动，对纵向舱壁的影响较大。

(5) 最大剪力的位置也出现在滚轮对应区域，和理论分析方法相符。

(6) 该文中提及的计算方法，可以快速准确的进行悬臂梁结构强度分析，对悬臂梁的设计有一定的指导作用。

[1] American Bureau of Shipping. Rules for building and classing mobile offshore drilling units[S].2011.

Overall Structure Yield Analysis of a Jack-up Cantilever

FENG Qi1， CHEN Yan1， REN Kang-xu2， GUO Pei-jun1

(1. Honghua Offshore Oil & Gas Equipment (Jiangsu) Co., Ltd , Jiangsu Nantong 201206， China；2.Shanghai Shipbuilding Technology Research Institute, Shanghai 200032, China)

The overall structural strength analysis of a jackup cantilever structure is presented in this paper for the cases of different cantilever positions and various drill floor offsets according to the ABS rules. The analysis is performed using a commercial finite element software ANSYS and hand calculation. Non-linear springs are used to simulate polymer which has non-linear mechanic property .Iteration method is used to calculate the general moment and von mises stress which are caused by dead loads and variable drilling loads. Two method calculations prove the methods in this paper can make cantilever strength analysis fast and acceptable and give reference for future cantilever basic design.

jack-up; cantilever; overall strength; non-linear

2015-09-15

江苏省自然科学基金项目“自升式多功能服务平台研发”(BK20130399)。

冯 琦(1978-)，男，博士。

1001-4500(2015)05-0061-07

P75

A