自升式风车安装船站立状态总体强度分析

刘仁昌， 赵志坚， 王永刚， 李连亮， 黄金林

(中远船务工程集团有限公司， 辽宁 大连 116600)

自升式风车安装船站立状态总体强度分析

刘仁昌， 赵志坚， 王永刚， 李连亮， 黄金林

(中远船务工程集团有限公司， 辽宁 大连 116600)

该文阐述了自升式结构物在站立状态时船体结构总体强度分析的基本理论和方法，对自升式风车安装船在站立状态下的船体结构总体强度进行了评估。基于风浪流环境条件和插深的设计依据，确定了自存、作业和预压载三种设计工况下需开展的计算工况。在船体结构总体强度分析中考虑了动态放大载荷的影响和非线性放大以及P-delta效应的影响，并对船体梁的中垂变形量进行了分析。结果表明，船体结构在站立状态下的总体强度和刚度满足了DNV规范要求。

总体强度；自升式风车安装船；动态放大；非线性放大；刚度

0 引言

随着海上风电应用技术的不断发展和成熟，海上风电清洁能源在近几年得到了大力的推广和应用。海上风场的建设和维护需要通过风车安装船来完成，风车安装船也成为近几年全球海工发展的重要方向之一。该文研究的风车安装船采用自升式船形结构物设计，包括4条圆筒形桩腿和液压顶升系统、起重能力为900 t的主吊，主吊以环绕桩腿的方式布置在左舷尾部桩腿位置。

风车安装船的设计工况包括自航工况、从漂浮状态到站立状态的安装工况、风车安装作业工况、自存工况以及从站立状态回到漂浮状态的回复工况等[1]。对于自升式结构物，需要同时对船体漂浮状态和站立状态进行整体强度评估。该文针对站立状态(包括自存、作业和预压载三种工况)下船体结构的总体强度进行分析和校核，并对船体梁的中垂变形进行评估[2]。

1 风车安装船主参数

总长：133.1 m；型宽：39.2 m；型深：9.8 m；桩腿长度：81.0 m；桩腿直径：4.7 m；最大载重量：5 100 t。

2 自升式结构物站立状态总体强度有限元分析方法

自升式结构物站立状态包括自存、作业和预压载三种设计工况。参考DNV规范[1]的工作应力法可以确定三种设计工况下需要开展的强度分析工况，见表1、表2。

表1 设计工况与装载工况

注： (1)预压载包括在自升式结构物安装过程中； (2) X表示需要开展计算的装载工况。

表2 装载工况介绍

工作应力法是通过将不同载荷类型进行组合后的各种工况下计算得到的应力跟材料的最大许用应力相比较，达到结构强度校核目标的一种方法。结构材料的屈服强度乘以许用的利用率系数得到对应的最大许用应力值。

参考DNV规范[1]，最大的许用利用率系数ηP可由下式计算得到：

(1)

式中：η0为基本利用率系数，见表3；β是一个依赖于结构类型、失效形式和结构构件柔度来确定的系数，对于屈服失效形式和平板加筋板格的屈曲失效形式的校核β值取1.0。

表3 基本利用率系数

注： 在极端环境条件下无人操作的海工结构物，对于装载工况(b)基本利用率系数η0此时可以取为0.84。

对于自升式结构物站立状态的总体强度分析，主要介绍确定性的线性静态分析方法[3]。其优点是简单且适用于较为细化的大型整船结构有限元模型，并可以通过一些简易的处理措施将忽略掉的动态效应和非线性因素考虑进来，以保证站立状态总体强度分析的精度。这些动态效应和非线性因素包括波浪载荷引起的自升式结构物水平惯性力的动态放大效应，桩腿在垂向受压载荷作用下对桩腿变形和弯矩的非线性放大作用以及P-delta效应。

自升式结构物在站立状态时主要承受自重、风浪流载荷及海底地基的支撑载荷[4]，如图1所示。

对于自升式结构物的自重，在站立状态总体强度分析时需要选用甲板可变载荷最大时的满载状态，且甲板可变载荷布置在使得结构物总体强度最危险的可能存在的位置。

一般围绕自升式结构物360°来浪方向范围选择合适的角度间隔，确定来浪方向个数，且风浪流载荷在同一来浪方向下总是假定保持相同的作用方向。波浪在任意浪向下需要确定相位角间隔，一般取10°，在整个波浪的360°周期范围内分为36个相位位置，通过DNV的Sesam/Wajac软件搜索每个浪向下36个相位位置中的基底剪力和倾覆力矩分别为最大值的时刻进行强度校核。

风浪流载荷除了船级社规范要求外，一般按照所设计结构物的设计基础报告提供的环境条件进行选择。除了选用各个工况下对应的最大波高外，还需要考虑波浪周期范围跟结构物固有周期之间发生的动态放大效应。

参考DNV规范[3]，波浪周期与结构物固有周期之间共振引起的对结构物惯性力的动态放大效应可以通过动态放大系数和基底剪力计算，并将此载荷以水平力的方式施加到结构物重心位置，载荷施加方向与对应浪向下的风浪流作用方向相同，从而将动态放大效应叠加到了线性静态分析中。图2为基于基底剪力和动态放大系数的动态放大载荷求解。

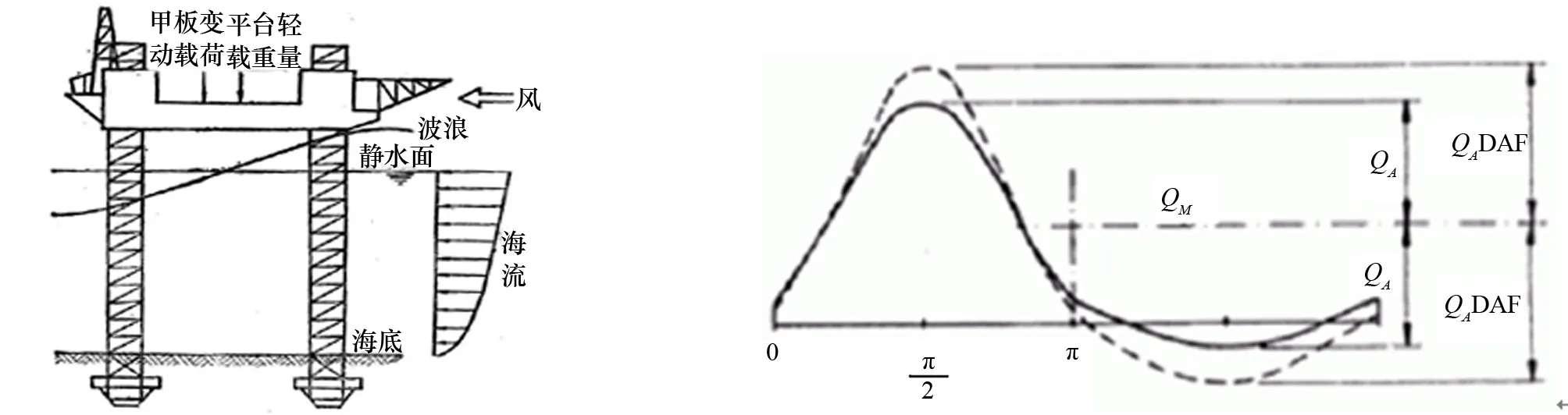
图1 自升式结构物载荷-站立状态 图2 动态放大载荷求解

在图2中：QM为总基底剪力的平均值；QA为总的基底剪力的幅值；DAF为动态放大系数；QA(DAF-1) 为基于基底剪力求得的动态放大载荷，将以水平力的方式施加在结构物重心位置。

动态放大系数的求解公式如下：

(2)

式中：T0为自升式结构物固有周期；T为波浪周期；ξ为自升式结构物处于站立状态时的阻尼比。

参考DNV自升式结构物规范[3]，阻尼比ξ可以取在6%～9%之间，且一般不大于7%；结构物与波浪发生共振时，考虑不规则波浪的影响，可以选用的阻尼比计算公式：

(3)

自升式结构物处于站立状态时，一般前三阶最低固有频率对应于结构物整体的纵向变形位移、横向变形位移和水平面内的扭转变形位移。求解动态放大载荷时一般选取此三阶固有周期进行动态放大系数的求解和最大值的搜索。

P-delta效应也可以通过施加在结构物上的一个水平力H来进行代替，代表P-delta效应的水平力计算公式如下：

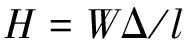
(4)

式中：W为自升式结构物在站立状态时从船底基线向上部分的总重量；Δ为某个风浪流作用方向上船体的水平位移；l为桩腿底端约束点到桩腿和船体连接点的垂向距离。对于上、下导向间存在锁紧系统的情况，桩腿和船体的连接点一般认为处于下导向到锁紧点间距离一半的位置；水平力H施加在距离底部约束点垂向距离为l的平面内，且作用点为总重量W的重心在此平面上的投影。

结构物水平位移Δ由下式求得到：

(5)

式中：α为非线性放大系数；eo为自升式结构物由于建造和安装过程中存在的误差和船体的倾斜导致的站立状态下船体相对于桩腿底部位置的水平相对位移，按照DNV规范要求[3]，eo一般不小于0.005l；e为站立状态下自升式结构物由于风浪流和动态放大作用引起的船体水平侧向的一阶位移。

非线性放大系数α由下式求得：

(6)

式中：P为单根桩腿承受的平均轴向载荷；PE为单根桩腿的Euler屈曲载荷。

海底地基对桩靴底部的支撑作用，在总体强度分析中一般可通过底部加约束的相对保守的简易方式模拟。约束点取桩腿入泥深度的一半或桩靴高度的一半处，取两者的较小值。考虑到海底泥土对桩靴的约束作用，在没有开展桩靴与海底土壤相互作用分析时，一般选用将约束点进行固支和铰支两种约束条件。

3 载荷与分析工况

3.1 环境载荷

环境载荷主要是风浪流载荷，自存、作业和预压载三种设计工况下的环境条件分别见表4、表5、表6。整船结构有限元模型通过Genie软件完成，整船有限元模型和风浪流载荷的施加如图3所示。

表4 自存设计工况环境条件

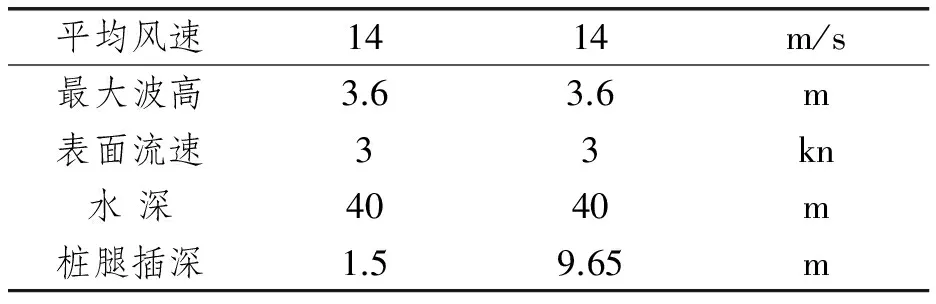
表6 预压载设计工况环境条件

表5 作业设计工况环境条件

图3 风车安装船有限元模型和风浪流载荷施加

3.2 动态放大效应与P-delta效应

在风车安装船的动态放大载荷求解中，阻尼比ξ分别按7%与13%两数值进行了考虑，整船固有周期则通过Genie软件的特征值分析计算得到，波浪周期考虑风车安装船设计给出的波浪对应的周期范围，在此基础上计算并搜索得到动态放大系数的最大值，并保守地应用于所有的计算工况。

对于风车安装船桩腿和船体之间采用插销加液压顶升系统连接方式的情况，该文基于对DNV规范的理解，将桩腿和船体之间的连接点设置于上下导向之间距离一半的位置，同时确定了l的值与代表P-delta效应的水平载荷H的施加位置。

图4 整船重量施加

3.3 其他载荷

除了环境载荷之外，在整船结构有限元模型中还施加了结构重量、甲板可变载荷以及液舱内液体的重量。整船结构重量和总的空船重量分别参考重量报告，对整船有限元模型进行调整，保证整船有限元模型中的质量分布跟重量报告保持一致。

自存和预压载设计工况时风车安装船甲板上承载的风车重量最大值为5 100 t，主吊不作业；作业设计工况时，主吊吊重900 t，吊重处于最大外伸位置，且考虑了主吊不同的旋转位置，转动角度间隔为45°，共8个转动角度工况，甲板上承载的风车重量则减为4 200 t。

在作业设计工况中，主吊吊重900 t，同时考虑了由于吊机旋转作业引起的动态放大作用，参考DNV规范[6]施加1.1倍的动态系数，整船重量施加如图4所示。

3.4 计算工况

参考站立状态的相关参数和总体强度分析的目标，判断和确定最危险分析工况的数据见表7，比较后确定的最危险分析工况见表8[7]。

表7 自存、作业和预压载设计工况中对总体强度产生影响的因素比较

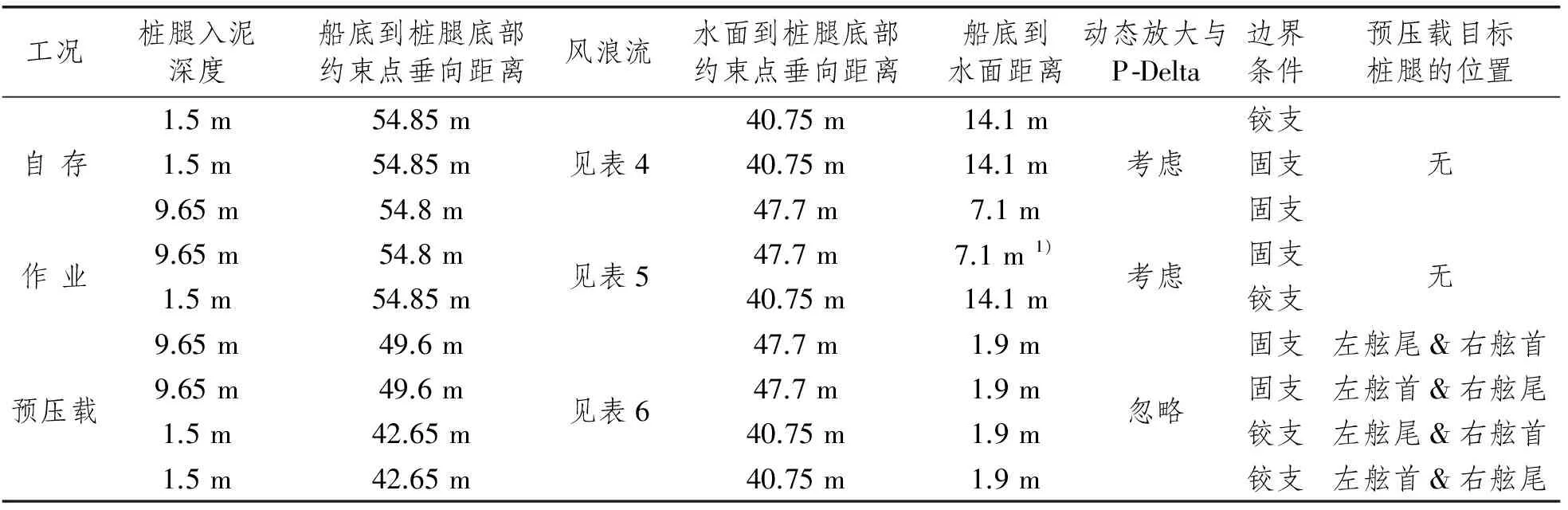
表8 自存、作业和预压载设计工况分别的最危险工况

注： 作业设计工况下，1.5 m插深时船底到水面距离14.1 m更大，因此在9.65 m插深目标分析工况时风速需要基于假定的船底高于水面14.1m的情况进行设置。

对于风车安装船的预压载，采取了对角两桩腿一起预压载的方式，并分别考虑被预压桩腿底部固支和铰支两种边界条件，分4次完成风车安装船预压载状态的总体强度分析。

预压载时,被预压的两条桩腿的目标调节载荷为所有自存和作业设计工况总体强度分析中得出的桩腿底部的最大垂向支反力，在预压载桩腿底部的垂向支反力达到目标调节载荷的同时，还需要考虑预压载设计工况对应的风浪流环境载荷，但预压载时没有考虑动态放大效应和P-delta效应。

考虑到4条桩腿呈长方形分布，风浪流作用方向采用45°间隔，从0°～360°的范围分为8个来浪方向，每个浪向的相位角间隔为10°，在波浪360°周期范围内分为36个相位位置。

在作业设计工况中，除了8个来浪方向外，主吊吊重900 t绕着风车安装船一周360°范围内也选择了8个位置，每两个位置之间的间隔为45°。浪向的定义如图5所示，主吊吊重900 t，在作业工况时的位置定义如图6所示。

图5 浪向定义 图6 主吊吊重900 t位置工况

4 总体强度分析结果

4.1 许用应力

整船船体结构(不包括桩腿和桩靴结构)用到的结构材料和许用应力见表9。

表9 船体结构许用应力

4.2 总体强度分析结果

在总体强度分析模型中桩腿简化为梁单元，船体结构通过壳单元模拟。总体强度有限元分析结果如图7、图8所示，两图皆为所在设计工况下所有计算工况的最大Von mises应力的搜索结果。

图7 装载工况(a) 中Von mises应力结果 图8 装载工况(b)中Von mises应力结果

图9 加筋板受力状态-面内应力与侧面压力

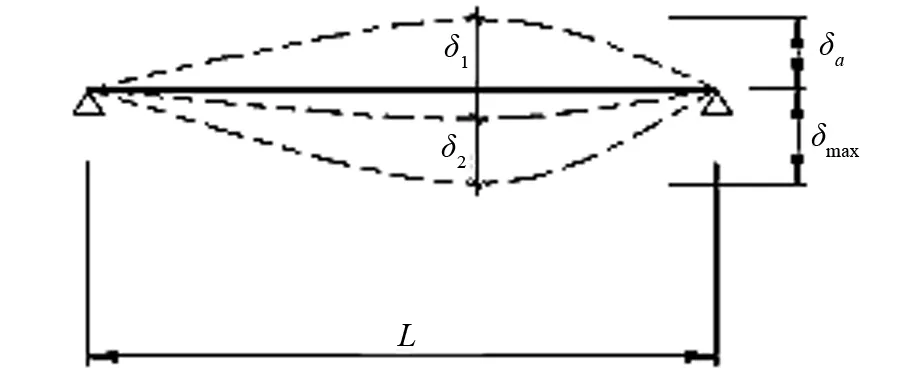
图10 垂向变形量示意图

4.3 船体结构屈曲强度

风车安装船处于站立状态时，船体梁整体主要产生中垂变形，甲板承受较大的面内压应力。此外，由于船体结构脱离了水面，底板和舷侧外板不承受垂直板面的侧向水压力作用，但主甲板承载较大的风机重量的侧向压力作用，主甲板结构受力状态如图9所示。因此，针对站立状态时最为危险的主甲板结构进行了屈曲强度校核。

应用根据挪威船级社规范[8]编制的后处理计算表格，对主甲板承载较大的板架结构的屈曲强度进行校核，包括加筋板格的整体屈曲、非加筋板格、大梁、筋等局部屈曲，校核结果显示主甲板结构满足屈曲强度要求。

4.4 船体结构中垂变形

参照DNV规范[2]，允许的最大变形量为δmax≤L/250，最大变形量δmax和跨距L如图10所示。

(7)

图11 船体结构中垂变形

式中：δmax为总的最大变形量；δ0为结构物设计的预起拱值；δ1为由于永久性载荷引起的变形；δ2为可变载荷引起的变形与永久性载荷引起的时效变形之和。

风车安装船桩腿纵向间距为70m，可求得允许的最大变形量为L/250=0.28m

计算得到的总变形量0.062m，远小于规范要求的许用值0.28m，所以船体梁在站立状态时的中垂变形能够满足DNV对结构变形量的刚度要求，船体中垂变形如图11所示。

5 结论

该文基于DNV和SNAME对自升式结构物在站立状态下的总体强度要求，结合风浪流环境条件、桩腿布置和作业特点，确定了自存、作业和预压载时需要进行校核的相关危险工况，计算得到了各工况下船体结构的整体应力水平，完成了船体结构部分的总体强度评估，结果满足了DNV和SNAME的规范要求，有如下分析和结论：

(1) 基于波浪载荷总的基底剪力和倾覆力矩为搜索目标的总体强度分析，确定工况时需要同时考虑风浪流载荷的大小、载荷作用位置(即力臂)、桩腿跨距和桩腿底部边界条件等多个因素的综合影响，载荷作用位置与桩腿跨距的确定跟桩腿入泥深度、水深、船底离水面的高度等有关。

(2) 对于4条桩腿的自升式结构物来说，桩腿距离更近的横向是产生桩腿和船体之间最大相互作用力的方向，在下导向位置处桩腿横截面上的弯矩主要依靠上下导向对桩腿的水平力作用形成的弯矩、顶升系统与桩腿连接的插销位置处的垂向力形成的弯矩来共同抵抗；在主要依靠上下导向对桩腿的水平力作用形成的弯矩抵抗桩腿横截面弯矩的情况下，上下导向间的垂向距离非常关键，也是设计初期升降室高度尺寸确定的一个重要参考因素。

(3) 相对于采用6条桩腿设计的船形自升式风车安装船，4条桩腿的设计不可避免的会出现较大的桩腿纵向间距，这时船体梁处于站立状态的中垂变形需要在设计初期重点关注，特别是对于大尺度、有较大甲板承载能力要求的风车安装船。

[1] DNV-OS-C201.Structural design of offshore units (WSD method)[S]. 2014.

[2] DNV-OS-C101. Design of offshore steel structure, general (LRFD method)[S]. 2011.

[3] DNV-RP-C104.Self-elevating units[S]. 2012.

[4] 李润培，王志农. 海洋平台强度分析[M]. 上海：上海交通大学出版社，1992.

[5] SNAME. Recommended practice for site specific assessment of mobile jack-up units[S]. 2007.

[6] DNV. Standard for certification N0. 2.22, lifting appliances[S]. 2013.

[7] 李红涛，李晔. 自升式钻井平台结构强度分析研究[J]. 中国海洋平台, 2010, 25(2): 28-33.

[8] DNV-RP-C201.Buckling strength of plated structures[S]. 2010.

Jack-up WTIV Global Strength Analysis in Elevated Conditions

LIU Ren-chang, ZHAO Zhi-jian, WANG Yong-gang,LI Lian-liang, HUANG Jin-lin

(COSCO-Shipyard Group Company Limited, Liaoning Dalian 116600, China)

The theory and methodology of the global strength analysis for Jack ups in elevated conditions are introduced, and the global strength for the jack up WTIV in elevated conditions is verified. Based on the environmental conditions and the penetration prediction of the project, relevant load cases are confirmed for the survival, operation and pre-loading design conditions. In the global strength analysis the dynamic amplification effect, non-linear amplification and P-delta effect are taken into account. The hogging deformation of the hull structure is also assessed based on the analysis result. From the result it can be shown the global strength and the rigidity of the main hull structure in elevated conditions fulfill the requirement of DNV offshore rules.

global strength; jack-up wind turbine installation vessel(WTIV); dynamic amplification; non-linear amplification; rigidity

2015-05-25

工信部高技术船舶科研项目(工信部联装2011536号)。

刘仁昌(1980-)，男，工程师。

1001-4500(2015)04-0093-08

U69

A