基于振动测试的自升式平台模态分析研究

曹文冉， 于麟川， 刘振纹

(1．中国石油集团工程技术研究院，天津 300451；2．中国石油天然气集团海洋工程重点实验室，天津 300451)

基于振动测试的自升式平台模态分析研究

曹文冉1, 2， 于麟川1, 2， 刘振纹1, 2

(1．中国石油集团工程技术研究院，天津 300451；2．中国石油天然气集团海洋工程重点实验室，天津 300451)

以自升式平台为研究对象，开展了结构振动检测实验，结合三维软件模型，引入增强频域分解方法对平台进行了模态识别，并研究了质量对各阶模态频率影响的灵敏度。计算表明，通过关注灵敏度高的测点或阶次的改变可以了解结构性能的变化，从而为海洋工程结构强度评估工作提供了重要的补充手段。

增强频域分解法；自升式平台；模态分析；灵敏度

0 引言

结构振动检测获得的数据结果，很难通过对数据的直接观察获得与结构性能相关的参数，只能大致判断出结构受迫振动的基频，而结构的自振频率又很难根据数据直接观察得到。因此，要对振动检测数据和结构振动各阶次模态进行深入的计算，才能了解与结构强度有关的更多信息，此时就需要利用模态分析手段进行相应计算[1，2]。

频域分解技术可以在均值白噪声激励和结构小阻尼条件下通过振动响应进行模态估计，但是不能得到结构阻尼比。为了克服这一缺点，增强频域分解方法利用逆傅里叶变换将响应的功率谱密度转化到时域来分析，通过计算自相关和互相关函数获得固有频率和阻尼比[3，4]。

该文以自升式平台为研究对象，开展了结构振动检测实验，结合三维软件模型，引入增强频域分解方法对平台进行模态识别，并研究了质量对各阶模态频率影响的灵敏度，旨在为国内类似平台的振动检测与安全评估研究提供借鉴和参考。

1 增强频域分解法(EFDD)

增强频域分解法(Enhanced Frequency Domain Decomposition method，简称EFDD)是由峰值拾取法(Peak Picking method，简称PP)发展而来，是一种白噪声激励在频域识别参数的方法，能够在保留用户采用频域法处理数据的同时，识别PP法所无法识别的密集模态，得到更加可信的系统阻尼比[5，6]。

EFDD法作为FDD法的改进，其原理是将每条谱线的响应互功率谱密度矩阵进行奇异值分解，得到各单自由度(SDOF)模态的自功率谱密度和各阶模态的振型，由功率谱密度在峰值附近的区间便可确定模态的频率和阻尼。其操作也极其简单，和峰值拾取法类似，只要拾取峰值即可。和峰值拾取法不同的是，通过奇异值分解，EFDD方法能直接得到振型，从而识别密集模态。

对于每组测量数据，在各个频率下对响应谱矩阵行奇异值分解：

(1)

式中：[Σ]为奇异值对角阵；[Φ]=[{φ1}{φ2}{φ3}…{φr}]，奇异向量{φ}代表模态振型估计。

时域内的自由衰减函数用来估计第k阶模态的阻尼系数：

(2)

式中：rok为相关函数的初始值；rpk为第p个峰值。

与其他时域模态分析方法相比，EFDD法不会产生虚假模态，因此自提出以来便迅速得到了广泛应用，尤其适用于海洋平台等环境激励模态分析。

2 基于EFDD的自升式平台模态分析实验

2.1 实验模型

以某自升式平台为研究对象，按比例缩建，桩腿总高2 380 mm，均为等边三角形桁架结构，底部焊接直径为200 mm的圆形桩靴；甲板为三棱台型，尺寸为980 mm×1 310 mm。实验时，将模型底部埋于实验池内并分层夯实，埋深约500 mm，防止其移动产生噪声。自升式平台模型就位后的实验照片如图1所示。

2.2 实验过程

(1)传感器布置

在某根桩腿一侧，采用C型夹具将8个加速度传感器分别固定，并将其中1个传感器设为原点导纳点，目的在于多次加载时保持各传感器同步。安装位置应尽量避开振型节点，同时保证最下侧的传感器离开试验池表面至少200 mm以方便安装，传感器与被测结构表面要保持清洁。

(2)荷载施加

通过适配电缆将传感器与控制模块连接，在确保连接正常后，将各设备开启，打开信号采集软件，对各路传感器初始值进行调零，然后用铁锤敲击模型局部，观察各通道波形变化，从而判断线路连接是否有效、传感器工作是否正常。

待确认连接正确无误后，按照图2所示的实验流程施加荷载。利用铁锤在被测桩腿上从上到下选择不同部位进行敲击以施加瞬时冲击荷载，分两种工况分别加载：一是甲板横向位移无限制，二是甲板横向位移被限制(类似于靠船状态)。

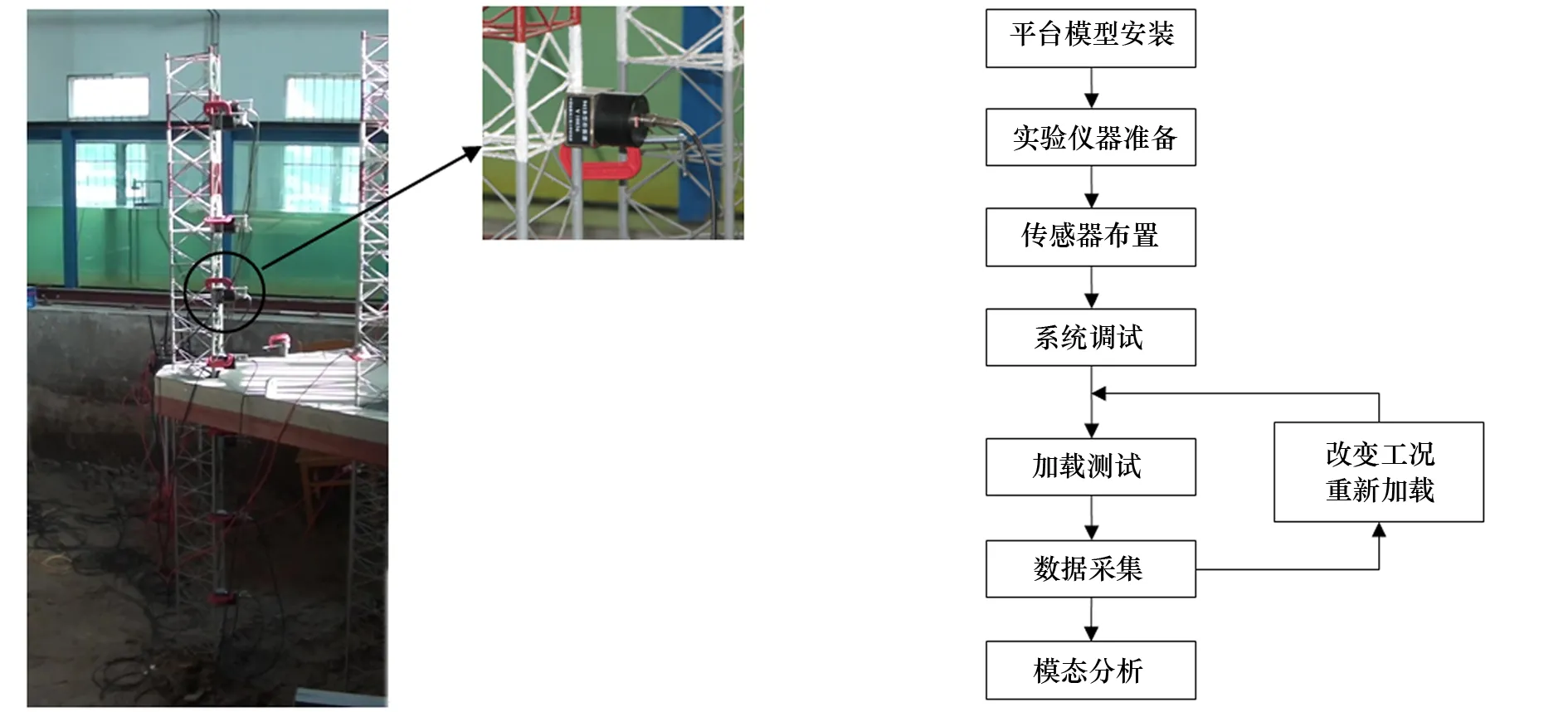
图1 自升式平台实验模型 图2 实验流程

2.3 实验数据

利用信号采集软件的回放功能，将实验数据导出至文本文件中。在瞬时冲击荷载作用下，8路传感器采集到的部分原始信号如图3所示。

图3 在瞬时冲击荷载作用下的8路传感器数据采集

2.4 模态分析

为了获取平台模型的模态振型，利用集成软件建立三维模型，将实验桩腿的7个节点与加速度传感器一一对应，其中原点导纳点传感器可不必与结构节点对应，自升式平台三维模型如图4所示。

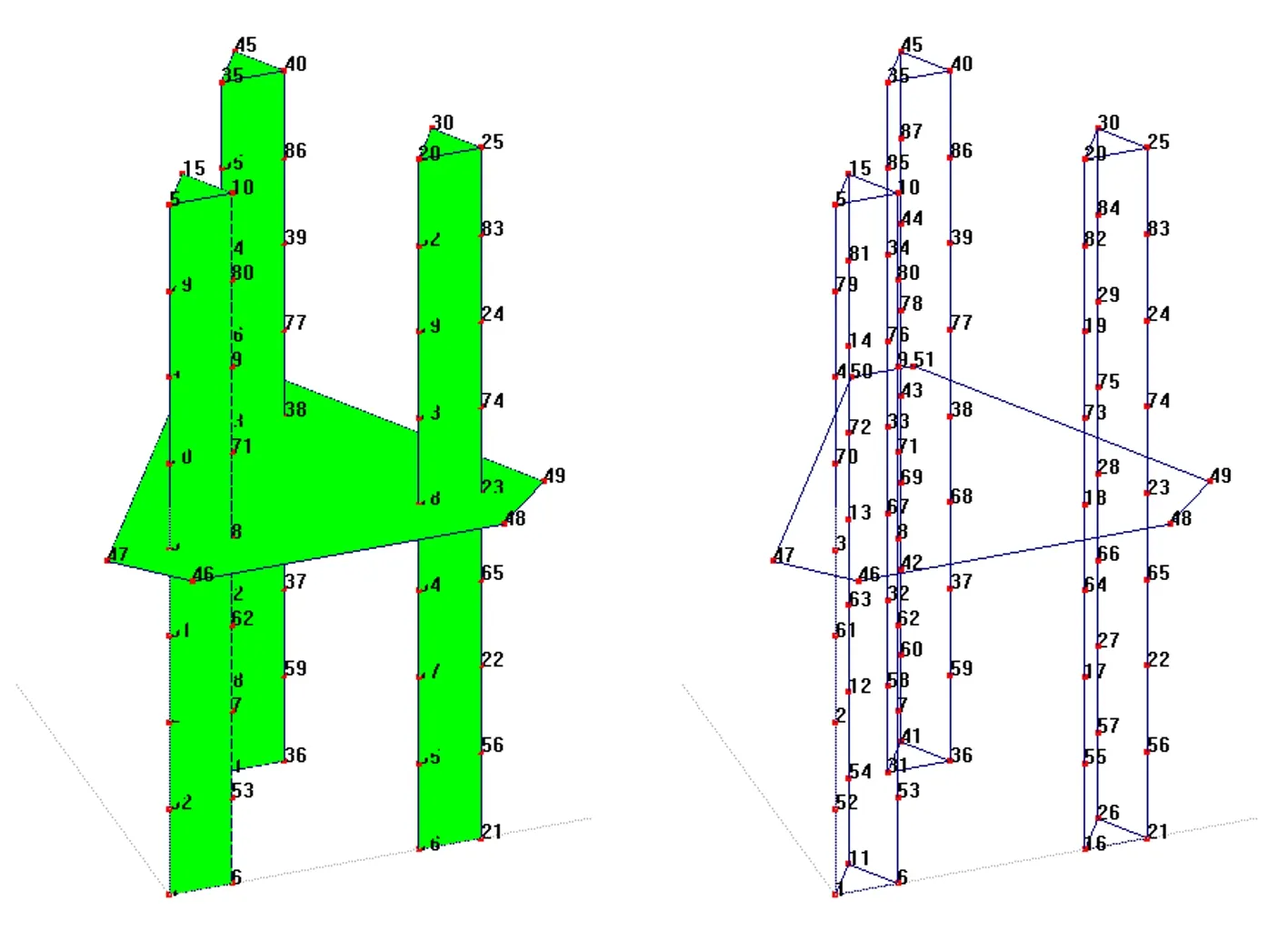
图4 自升式平台三维模型

利用信号处理软件对采集的加速度信号进行分解，分解后的奇异值曲线如图5所示，在峰值点即可拾取模态频率与阻尼比，见表1。

图5 两种工况下的奇异值曲线

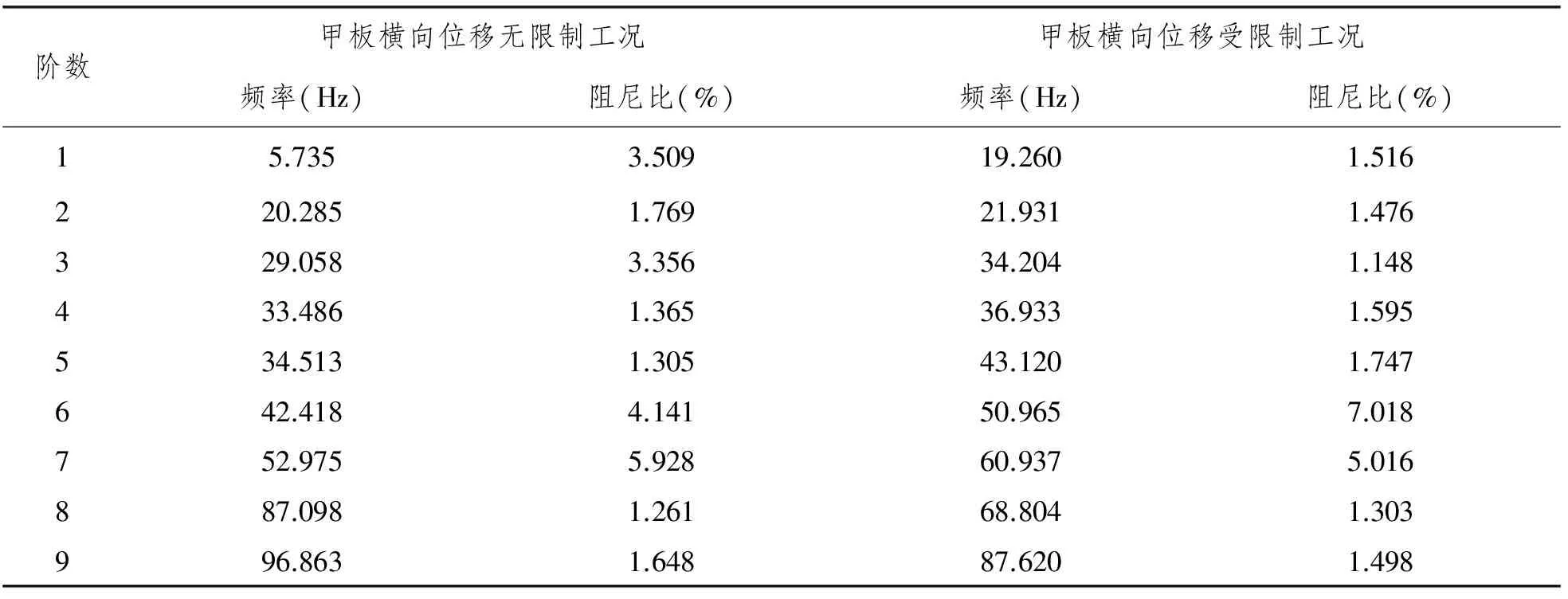
表1 各阶模态频率与阻尼比

以甲板横向位移无限制工况为例，通过分析各传感器测点的质量对各阶模态频率的影响就可以得到各阶模态的灵敏度，见表2。

表2 各阶频率对质量的灵敏度

将每个测点各阶频率的灵敏度绘制成曲线，如图6所示。

图6 各阶频率的灵敏度曲线

由表1可知，工况2的19.260 Hz大于工况1的5.735 Hz，说明甲板横向位移受限制会导致桩腿的一阶模态频率明显增大。

由图6可知，测点3的质量变化对各阶模态频率的影响均较大，而测点5的质量变化对9阶模态频率的影响最大，但是由于阶次较高，可能存在信号噪声与计算误差，因此可信度并不高。

3 结论

(1)以自升式平台模型为研究对象，开展了结构振动检测实验，采集了平台在瞬时冲击荷载作用下的振动响应，并建立了三维模型以便模态分析时各节点与传感器相互对应。

(2)基于增强频域分解方法，开展了自升式平台模态分析，研究了质量对各阶模态频率的影响，计算表明通过关注灵敏度高的测点或阶次的改变可以了解结构性能的变化。

(3)随着海洋平台结构检测技术的迅速发展，基于模态分析的振动检测技术必将成为结构强度评估工作的重要补充手段，因此该文开展的实验研究无疑具有重要的理论意义。

[1] 李洪涛, 史玉峰, 翟建习, 等. 海洋平台振动监测技术试验研究[J]. 中国安全科学学报, 2012, 22(12): 46-50.

[2] 徐士代. 环境激励下工程结构模态参数识别[D]. 南京：东南大学, 2006.

[3] 周凯. 基于环境荷载激励的海洋平台结构模态参数识别技术研究[D]. 青岛：中国海洋大学, 2009.

[4] 陈永会, 姜旭, 李海虹, 等. 基于试验模态的台钻动态特性研究[J]. 制造技术与机床, 2011, 61(12): 101-104.

[5] 陈旭丹. 基于无线传感的土木工程状态监测研究[D]. 上海：同济大学, 2007.

[6] Rune B, Zhang Lingni. Modal identification from ambient responses using frequency domain decomposition [C]. Proceedings of the18th IMAC. USA: Society for Experimental Mechanics, 2000.

Study of Jack-up Modal Analysis Based on Vibration Test

CAO Wen-ran1, 2, YU Lin-chuan1, 2, LIU Zhen-wen1, 2

(1. CNPC Research Institute of Engineering Technology, Tianjin 300451, China 2. CNPC Key Laboratory of Offshore Engineering, Tianjin 300451, China)

A test of structural vibration is proceeded for Jack-up and the modes are identified based on 3-D model and EFDD method. Then the sensitivity is studied between nodal mass and modal frequency, and the results obtained show that the change of structural performance can be inferred though the high level of nodal or modal sensitivity, which is an important mean of the structural assessment for offshore platforms.

EFDD; jack-up; modal analysis; sensitivity

2014-03-25

曹文冉(1984-)，男，工程师。

1001-4500(2015)04-0088-05

P75

A