锚泊系统起锚破土阻力分析

唐文献，吴文乐，张 建，王筱蓉，孙 泽，李金泰

(1.江苏科技大学 机械工程学院，江苏 镇江 212003；2.江苏扬远船舶设备铸造有限公司，江苏 泰州 225500)

锚泊系统起锚破土阻力分析

唐文献1，吴文乐1，张 建1，王筱蓉1，孙 泽2，李金泰1

(1.江苏科技大学 机械工程学院，江苏 镇江 212003；2.江苏扬远船舶设备铸造有限公司，江苏 泰州 225500)

为提高船舶在起锚过程中的效率与安全性，在经典理论公式基础上，通过ABAQUS软件模拟锚泊系统起锚破土过程，建立阻力数值分析方法，得出数值分析结果与土体流动机制。将阻力数值解与理论解进行对比分析。结果表明，数值分析方法比理论公式的结果更加符合预期效果，并且能够模拟土壤流动情况。

锚泊系统；起锚；ABAQUS；数值分析

锚泊系统是水上漂浮结构物必不可少的部分，能够在恶劣水域下抵御狂风、巨浪、暴潮，降低危险事故发生的概率。

正常起锚分5个阶段：①回收余链阶段；②收紧锚链阶段；③锚破土阶段；④收起悬锚阶段；⑤锚链入孔阶段。船锚破土是指将部分或全部侵入海床的锚取出的过程，而锚破土过程中的安全性对整个过程具有重要意义。在实际海上作业中，将锚从底质中拔出来的力越小越好，有利于减少船体和锚链的载荷，降低船只作业风险。若锚不能及时拔出，将会造成电机堵转，电流陡增，损坏电机。2014年7月，中国船级社CCS发布了《钢质海船入级规范修改通报》，对锚操作进行了补充规定，要求提高锚操作时的稳定性[1]。近年来，我国逐步加强对深海油气资源的开采，为保证海上钻井平台工作的稳定性，对锚泊设备提出更高要求，如何提高船舶在锚地起锚过程中的安全性已受到研究人员和相关机构的高度重视。

船舶用锚根据海底土壤不同具有较多种类[2]，本文在理论研究的基础上，以通用的霍尔锚为对象，采用CEL耦合方法，对船舶在起锚过程中土体的弹塑性变形进行研究，建立起锚破土阻力数值分析方法，所得结果对船舶顺利起锚具有重要意义，为船舶在起锚困难时提供破土阻力的计算依据，避免危险事故的发生。

1 起锚破土阻力理论分析

国内外学者对锚破土过程的阻力进行了深入研究，其中具有代表性的有浙江大学于晓杰提出的动摩擦模型理论、Terzaghi理论和ChaoMing Chi理论等，但前两种理论存在一定的局限性。动摩擦模型理论涉及到土-锚微观表面刚毛的接触特性，其参数如锚与土表面刚毛刚度系数等不易得到；Terzaghi理论未考虑锚爪的具体参数，如锚爪长度等[3-5]。因此这两种理论过于保守，难以指导实际工作。

由于入土锚杆的侧摩阻力相对锚爪所受阻力较小，那么在锚卸扣处所受的力就等于在锚爪参考点所受力，ChaoMing Chi综合考虑了锚和非均质土的影响因素，在Terzaghi等人的基础上，以恒定速度起锚，从内部耗能的角度研究了锚在参考点所受力的大小[6]。其内部速度能量场与受力情况见图1。

由图1可见，锚爪被简化成AB杆，锚爪抓土后与水平面夹角为θf；α为能量场的刚性楔角。A点附近的内部耗能发生在可变形区域(3)和滑移表面(1)、(2)和(4)。同样，B点附近的内部耗能发生在可变形区域(7)和滑移表面(5)、(6)和(8)。C点为锚爪重心，也是参考点。

根据弹塑性变形全量理论与Tresca屈服极限推出单位体积内部能耗为

D=Suv0L

(1)

式中：D——内部能耗；Su——不排水抗剪强度；L——滑移表面长度。

那么垂向载荷Fn所产生的能耗就等于总内部能耗：

Fnv0=D1+D2+D3+D4+D5+D6+D7+D8

(2)

因此，垂向载荷为

(3)

由于土体在泥水分界处的不排水抗剪强度不为零，且随着深度变化逐渐变大，满足公式[6]：

(4)

式中：k——土壤的强度梯度；z——锚爪的埋深；Su0——泥水分界处的不排水抗剪强度。

起锚拉力主要由锚链提供，为竖向载荷。所以，根据式(3)和(4)得破土阻力公式：

(5)

该公式充分考虑了土-锚系统的综合特性，能够为锚泊系统起锚破土阻力的预测提供理论基础。但是实际海况复杂多变，使得计算出的阻力值难以与实际情况完全一致。因此，为了更好地计算出破土阻力，本文在沿用理论公式的基础上，采用数值分析方法，模拟起锚破土过程，并将理论解与数值解进行对比分析。

2 土-锚系统的有限元数值模型

ABAQUS软件能够针对土体的变形与渗流进行耦合分析，渗透定律则采用Forchheimer非线性定律或Darcy定律。为了能够有效模拟土-锚系统阻力变化，在考虑流固耦合情况下，进行数值模拟计算[7-9]。

2.1 土-锚系统模型

本文研究对象为典型的霍尔锚，最大高度为7.1 m，锚爪高度H为3 m，锚身厚度B为2.2 m，锚爪展开角度α为45°，锚的最大宽度D为5 m。为避免边界效应，取土体模型宽度L=10D，取深度h=5D，见图2。

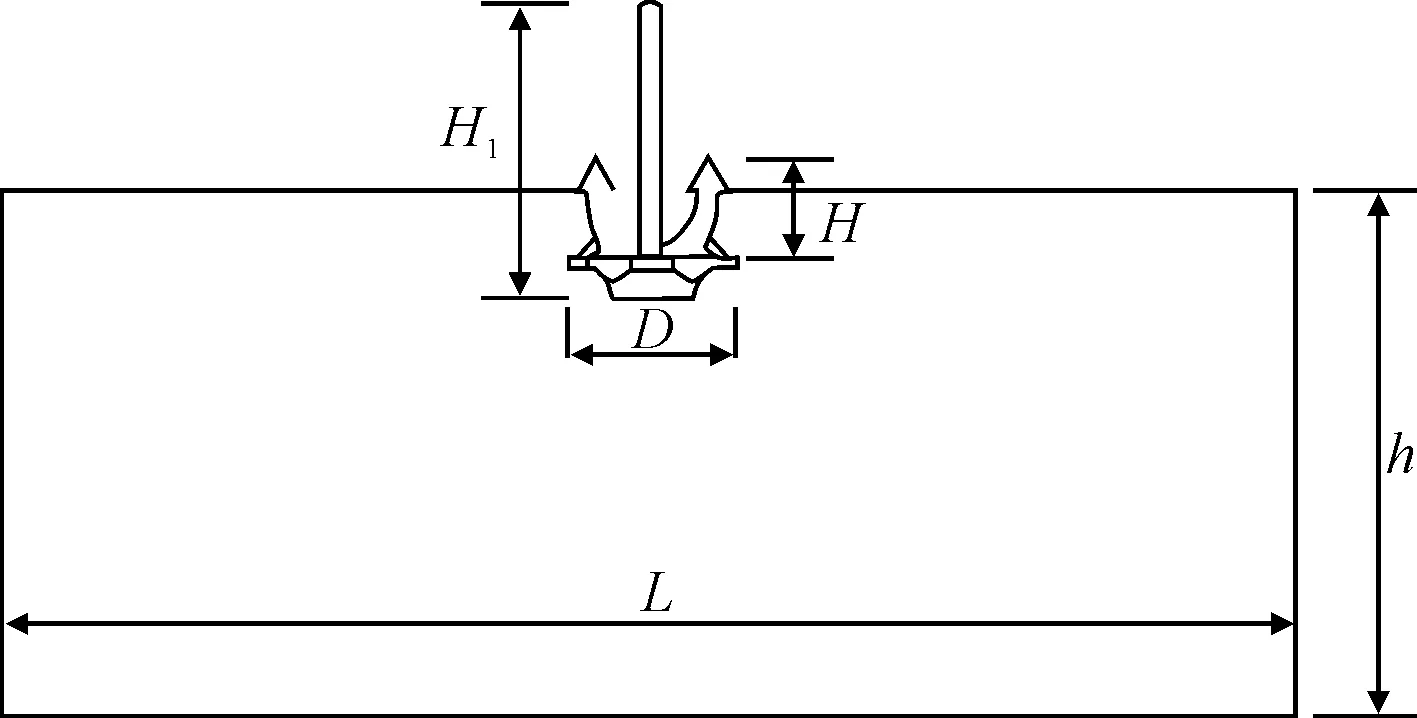
图2 土-锚系统参数图

利用ANSA软件对实体进行网格划分，霍尔锚网格以六面体缩减积分单元C3D8R为主，局部采用四面体网格离散。由于锚的破土过程为大变形问题，土体的变形程度远远比锚的变形程度大得多。因此，在有限元软件模拟起锚过程中，可以将锚的整体结构设置为刚体，采用恒定速度起锚，加载方式为在船锚卸扣处施加速度边界条件。

海洋里土层基本是多层土壤构成的交叉状态，本文将多层土地基简化成单土地基进行计算。土体网格综合拉格朗日与欧拉网格的优点，借鉴CEL方法进行分析,选用Mohr-Coulomb模型，将土体单元类型设置为欧拉六面体缩减积分单元EC3D8R[10]。高度主要分为3层：第一层模拟水域，设置为空穴，即无任何材料属性，空穴深度对计算结果几乎没有影响，网格设置最为密集，用来模拟土体在起锚过程中的土体流动及隆起情况；第二层为软土，破土过程主要发生在该层，为土体的大变形区，对破土阻力影响较大，网格较为密集；第三层与第二层同为软土，由于对起锚阻力影响较小，为了减小计算时间，网格设置较为稀疏。考虑到土体的自重问题，需要对模型平衡地应力，并设置土体的边界条件。ABAQUS有限元模型见图3。

图3 土-锚系统的有限元模型(隐藏空穴后)

2.2 土-锚系统材料参数

锚材采用铁质、弹塑性材料，密度ρ=7 900 kg/m3，弹性模量E=200 GPa，泊松比υ=0.3。

土体材料：土体为软土，弹塑性材料，密度为ρ=1 800 kg/m3，弹性模量E=5.5 MPa，泊松比为v=0.49，内摩擦角φ为10°，初始孔隙比为1，有效容重γ′=7.4 kN/m3，泥水分界处的抗剪强度Su=1.5 kPa，土壤的强度梯度k=1 kPa/m。

2.3 锚的初始埋深

在研究起锚过程时，锚的初始埋深对计算结果存在影响，同时为避免对海底管线和电缆的损坏，需要对船锚的初始埋深进行计算[11]。根据《广东省沿海航道通航标准》，船舶在应急情况下抛锚的入土深度为2～4 m。一般霍尔锚的入土深度满足经验公式：

(6)

式中：T——锚的入土深度；H——锚爪的高度；α——锚爪展开角度；B——锚身厚度。

结合本文中使用的霍尔锚模型，锚爪高度H为3 m，锚爪展开角度α为42°，锚爪厚度B为2.2 m，则锚的入土深度为3.3 m，且在《广东省沿海航道通航标准》范围之内。

3 起锚破土结果分析与讨论

3.1 理论结果分析

由于式(5)中不排水抗剪强度和锚爪抓地夹角为不定值，为了简化计算，有限元计算中将锚爪抓地夹角设为定值。因此，在理论计算过程中，同样将夹角设为定值。而对于不排水抗剪强度的影响，主要与埋深有关，在有限元模拟中是以恒定速度起锚，因此埋深随时间呈线性变化，最终阻力为

(7)

式中：h——锚爪初始深度；v——起锚速度；t——时间变量。

结合数值分析中的数据，经计算得出，破土阻力呈线性变化。

F=142-13.7t

(8)

3.2 数值结果分析

将模型提交计算后，得到一条上下波动但呈下降趋势的阻力曲线。为方便描述，通过ORIGIN软件拟合出一条符合实际解的光滑阻力趋势曲线，见图4。由图4可见，以恒定速度起锚时，初始阶段船锚位于最深处，起锚阻力最大，下降趋势较为缓慢；当起锚作业时间到1.5 s左右，船锚上拔至1.5 m处时，阻力下降幅度明显增大，由于在模型的计算过程中考虑了船锚的自重，因此破土后阻力不会消失。而在实际情况中，当锚完全脱离土壤以后，锚的回收还需克服锚链重量以及海流的阻力，这在模型中未予体现。

图4 起锚破土阻力随深度变化

3.3 理论与数值解对比分析

为了确保结果的准确性，将数值解(拟合出的平滑曲线)与经典理论解进行对比，见图5。经典理论公式呈线性变化，且在初始阶段理论解明显较大，达到142 kN。这是由于在实际海洋底质中，土体的不排水抗剪强度的变化并非是线性关系，以及在泥水分界处不排水抗剪强度的标准不一。如果想要得到真实的抗剪强度，需进行原位测试或室内试验，如十字板剪切试验和三轴剪切试验等。而对于刚性楔角α，也是基于经验所得，对结果同样存在缺陷，因此线性理论解过于保守。而数值解是模拟真实起锚过程，虽然计算原理不同，但是两者的计算结果也非常接近，因此数值解更加符合实际情况，为锚链的强度校核与锚机的动力选择提供依据，保证船舶海上作业的安全性和稳定性。

图5 理论与数值解对比

3.4 起锚土体流动分析

图6为船舶起锚破土过程中土体的流动情况。上方为水域，无任何材料，用来模拟土壤的隆起情况；下方区域为土体。

图6 土体流动示意

由图6可见，在破土的初始阶段，由于土体边界较广，此时船锚的埋深最大，起锚只会影响周边土体，造成剪切破坏，土体开始流动，如图6a)。而土体随船锚上拔至一定深度，土体剪切破坏扩展到泥水分界面处，海底表面将会形成隆起，如图6b)。由于船锚上部存在覆土，因此在上拔的过程中，部分淤泥将会向下流动到船锚底部，造成土体回流，形成一个空腔，同时船锚上部分覆土也会随着上升一起离开海底层，如图6c)。因此，数值分析可以充分体现土壤的流动特性，弥补理论公式的缺陷，为进一步研究破土阻力变化提供基础。

4 结论

1)国内外学者对锚破土的理论研究存在缺陷，ChaoMing Chi理论公式从速度能量场的角度，综合考虑锚与土的条件参数，推出理论公式，其结果与真实解较为接近。但是完全呈线性变化的不排水抗剪强度与实际不相符，同时破土阻力还受到船锚下方土体水和土体表面水的影响，容易产生误差，不利于准确预测阻力变化。

2)数值解是以实际情况模拟起锚破土过程，所得结果呈非线性的下降趋势，能够较为精确地判断阻力变化。综合对比两种解，其阻力变化趋势相同，但变化幅度不一。数值解在初始阶段变化较为缓慢，而起锚到一定深度时，阻力值急剧下降。与理论值相比，数值解能够更好地反应船锚在破土过程中的阻力随深度变化情况，且能够真实反应土体的流动情况，从而可以保证锚链与锚机的正常运作，对船舶海上作业具有重要意义。

[1] 中国船级社.中国钢质海船入级规范修改通报[S].北京:人民交通出版社,2014.

[2] 叶邦全.海洋工程用锚类型及其发展综述[J].上海造船，2012(3):1-7.

[3] 于晓杰.浅海工程船移锚作业系统建模分析与仿真技术研究[D].浙江大学,2013.

[4] Canudas De Wit,OLSSON H,ASTROM K J,et all A new model for control of systems with friction[J].Transaction on Automatic Control, 1995,40(3):419-425.

[5] Canudas De Wit,LISCHINSKY P.Adaptive friction compensation with partially known dynamic friction model[J].International Journal of Adaptive Control and Singnal Processing,1997,11:65-80.

[6] CHI ChaoMing,Plastic limit analysis of offshore foundation and anchor[D].Texas A&M University,2010,8.

[7] 丁红岩,乐丛欢,张浦阳.海上自升式钻井平台拔桩阶段桩靴上拔阻力的机理研究[J].天津大学学报,2011,44(4):325-330.

[8] SLOAN MERIFIELD R S,S W.The ultimate pullout capacity of anchors in frictional soils[J].Can Geotech J,2006,43(8):852-868.

[9] ZHOU X X,CHOW Y K,LEUNG C F.Numerical modeling of breakout process of objects lying on the seabed surface[J].Computers and Geotechnics,2007,35(5)：686-702.

[10] 王 懿,贾 旭,黄 俊,等.基于CEL的船舶抛锚入泥深度分析[J].石油机械,2014,42(12):44-47.

[11] 谭 箭,李恒志,田 博.关于事故性抛锚对海底管线损害的探讨[J].船海工程,2008,37(1):142-144.

Resistance Analysis of Lifting Anchor Ground-breaking Process for Mooring System

TANG Wen-xian1, WU Wen-le1, ZHANG Jian1, WANG Xiao-rong1, SUN Ze2, LI Jin-tai1

(1. School of Mechanical Engineering, Jiangsu University of Science and Technology, Zhenjiang 212003, China;2. Jiangsu Yangyuan Boat and Ship Equipment Casts Co. Ltd., Taizhou Jiangsu 225500, China)

On the basis of classical theoretical formula, the lifting-anchor ground-breaking process of mooring system is simulated by ABAQUS to establish the resistance numerical analysis method. The numerical results and the soil flow mechanisms are obtained. The numerical results of resistance are compared with that of theoretical formulae, showing that the numerical method is more accurate and reasonable.

mooring system; anchor; ABAQUS; numerical analysis

10.3963/j.issn.1671-7953.2015.06.008

2015-09-30

江苏省自然科学基金项目(BK20150469)

唐文献(1962-)，男，博士，教授

U664.4

A

1671-7953(2015)06-0031-05

修回日期：2015-10-10

研究方向:海洋工程装备设计与制造技术

E-mail:tangwenxian@163.com