基于CFD的某内河游船风载荷系数计算

陈前昆,尹奇志,范爱龙,严新平,郑 杰,王 瑞

(1.武汉理工大学 a.能源与动力工程学院可靠性工程研究所； b.船舶动力工程技术交通行业重点实验室；c.能源与动力工程学院，武汉 430063； 2.重庆市巴南区港航管理处，重庆 401320)

基于CFD的某内河游船风载荷系数计算

陈前昆1a,b,尹奇志1a,b,范爱龙1a,b,严新平1a,b,郑 杰2,王 瑞1c

(1.武汉理工大学 a.能源与动力工程学院可靠性工程研究所； b.船舶动力工程技术交通行业重点实验室；c.能源与动力工程学院，武汉 430063； 2.重庆市巴南区港航管理处，重庆 401320)

为获得船舶风载荷系数的准确计算方法及其在不同风向角下的分布规律，以某内河船舶为研究对象，对船舶水上结构表面风场风压进行数值模拟，得到不同风向角下的风载荷系数，将计算结果与Fujiwara和Blendermann方法对比,结果表明，k-εRealizable湍流模型在计算风载荷系数时准确度较高；随着风向角变化，船舶风载荷系数变化较大；所采用的数值计算方法及网格形式可较好预报游轮风阻力。

内河游船；风载荷系数；数值模拟；流场分析

随着国际海事组织(International Maritime Organization，IMO)提出的新船能效设计指数(energy efficiency design index，EEDI)及营运能效指数(energy efficiency operational index，EEOI)等通函的逐步实施[1]，船舶节能减排成为船东、船厂以及船舶设计工作者关注的热点[2]。船舶在航行中所受阻力根据介质的不同可以分为风阻力和水阻力。船舶风阻力在总阻力中比重虽小，但是其对船舶推进性能、船舶操纵性能也有较大的影响。同时，随着绿色船型设计研究的逐步深入，为更多挖掘优化空间，提高能效以适应EEDI的需求，船舶风阻优化逐渐得到船东和航运企业的关注，风阻研究对船舶航行安全和减阻降耗都至关重要[3-7]。

当前，理论分析法、风洞试验和CFD方法是研究船舶风阻的主要方法。理论分析的结果一般带有普遍性，需要抽象和简化计算对象才能得到理论解。风洞试验虽然能得到真实、可靠的试验结果，但其操作周期性长、费用高、操作复杂，而且还不能直观地观察流场。相比之下，CFD数值模拟方法则能成功弥补上述两种方法的不足，费用少，重复性好，而且可以模拟复杂结构表面的风压分布及其周围的空间流场情况[8-10]。

利用CFD方法进行风载荷计算方面，在研究对象上，从最初的一些小型帆船，到后来逐步向大型油船、集装箱船和LNG船等船型发展；在研究内容上，学者在利用数值模拟方法开展计算时，对不同船型的计算策略，也都进行了较为全面和深入的探索[11-13]。然而，CFD方法在对游轮这一船型上的研究极少，不同船型之间CFD方法的计算策略可能会有较大差异，且游船载客量大，其安全性备受瞩目。本文以具有代表性的某内河游船为研究对象，基于CFD方法对对象船舶进行数值模拟研究，探索不同网格划分形式，不同湍流模型对数值模拟计算结果的影响，对比经验公式与数值模拟方法的计算结果，并分析船舶数值流场信息，为游轮风阻力及力矩的精确计算提供参考。

1 船舶风载荷系数与经验公式

1.1 船舶风载荷和风载荷系数

风载荷对于船舶的影响，主要体现在增加其在航行过程中的风阻力上，在对船舶风载荷的研究中，主要关注船舶水线以上结构所受到的纵向力、横向力和艏摇力矩，见图1。

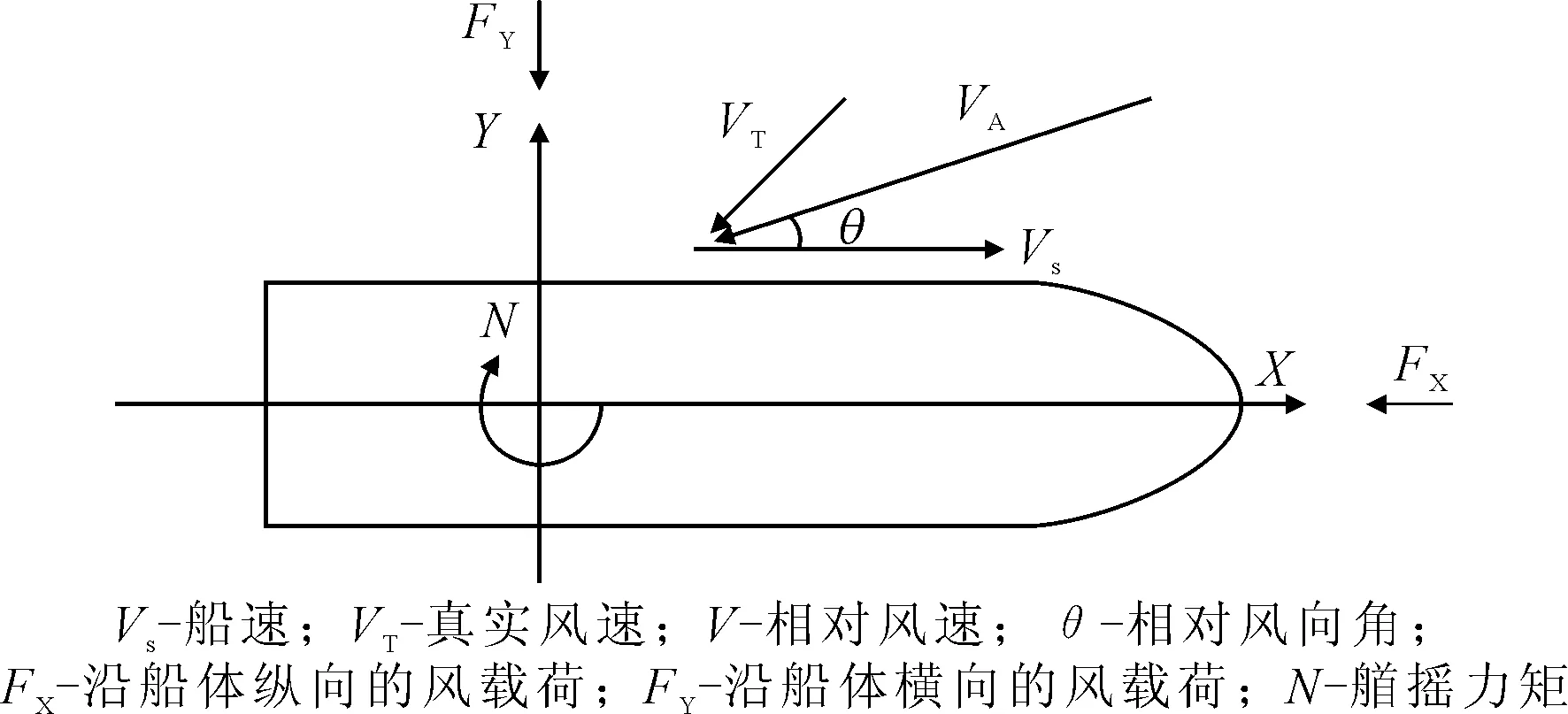
图1 船舶风载荷示意

为使风阻的计算结果便于在不同船舶尺寸和不同风速风向下进行对比，计算得到的风阻力通常以经过处理的无量纲系数表示，该系数直接决定了船舶受风阻力大小，如下式所示[14]。

(1)

(2)

(3)

式中:CX、CY、CN——纵向、横向风载荷系数、艏摇力矩系数；

ρ——空气密度;

LOA——船长;

AL、AT——船舶正纵、正横时的受风面积。

1.2 经验公式

目前计算风载荷系数的经验公式主要有：Isherwood方法、Blendermann方法、OCIMF公式、Fujiwara方法、范·伯利柯姆公式等，从中选择普遍认为具有较高精度的Fujiwara和Blendermann方法作为对数值计算结果的参照[15-18]。

2 数值模型

2.1 船型参数及计算模型

选取内河一艘游船为算例进行风载荷系数研究，其主尺度列于表1，典型工况选为满载。

表1 对象船舶主尺寸 m

利用FLUENT前处理软件GAMBIT进行建模。考虑到结构的复杂性，几何建模时对受风阻影响较小的构件进行简化，简化后的模型见图2。

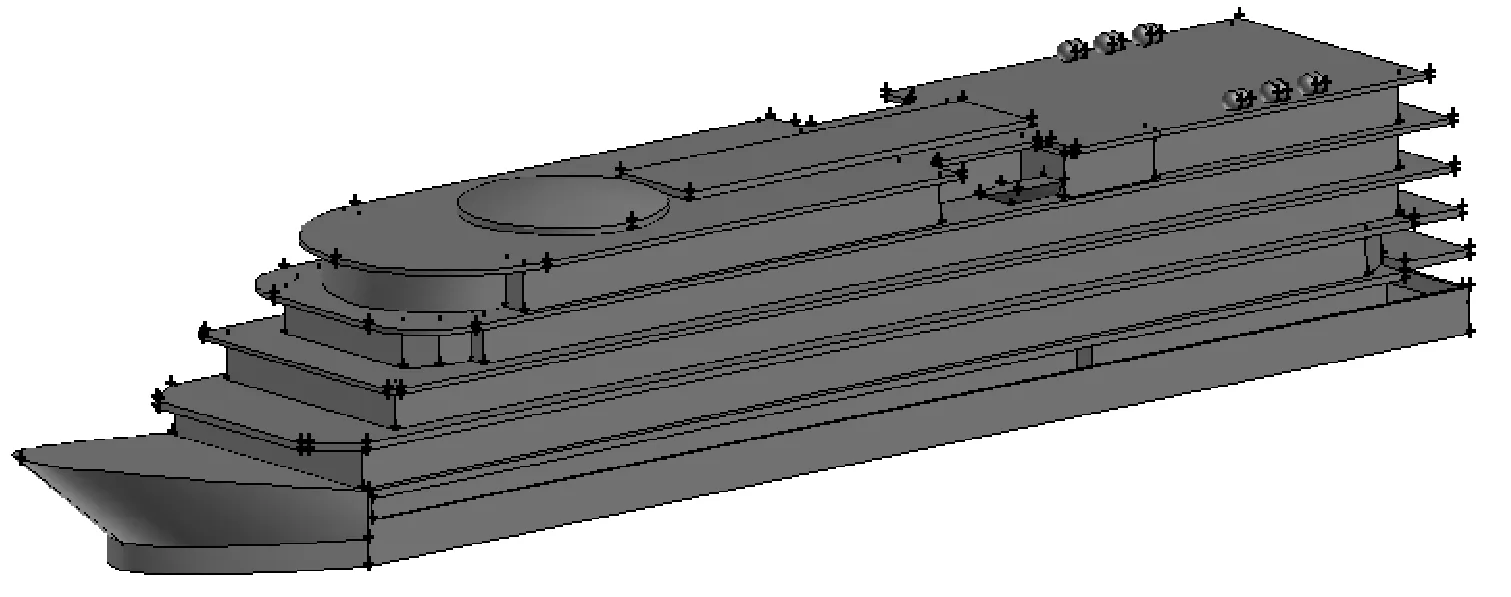
图2 对象船舶几何模型

2.2 计算域设置及网格划分

根据国际拖曳水池会议(international towing tank conference，ITTC)临时规程，在研究网格数量对计算结果的影响时，至少要采用密度不同的三套网格。本算例建立三套网格，设置形式见表2。

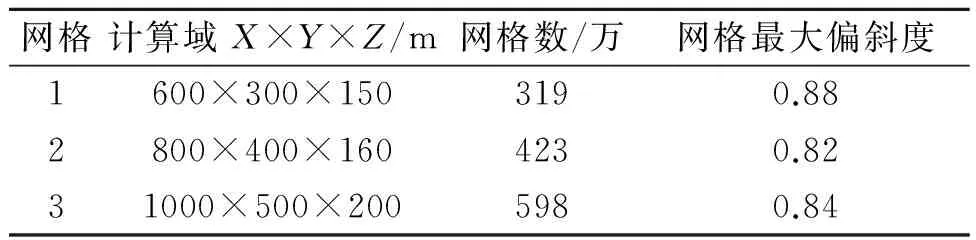
表2 三套网格的基本情况

为方便计算不同风向角下的风载荷系数，在对模型进行流域构造时，将计算域分成内域和外域，船舶模型置于内域中，将内域设计成圆柱体形，能围绕其轴心做任意角度旋转，见图3。

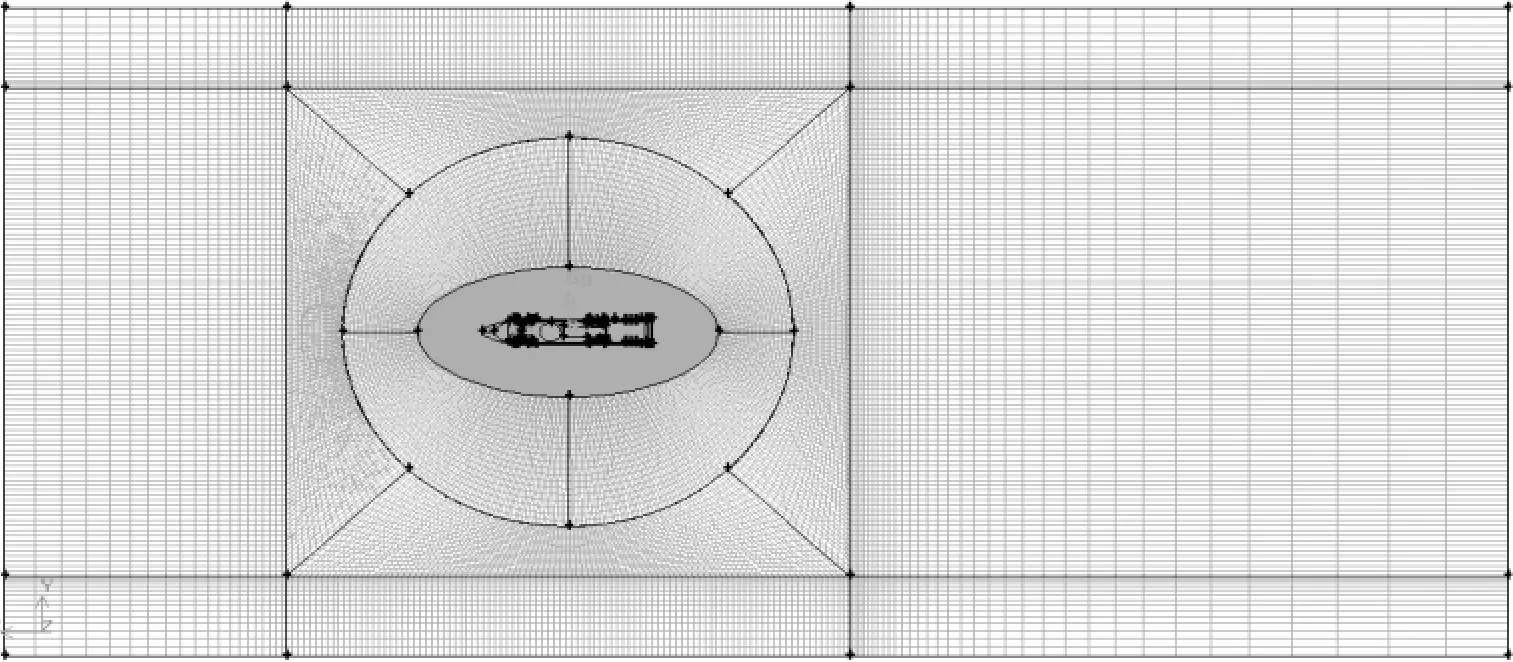
图3 流域及网格设置示意

在网格划分时，采用混合网格以提高计算精度：内域模型结构复杂，采用非结构网格；外域结构简单，采用结构网格。

2.3 湍流模型及边界条件

目前湍流数值模拟方法分为直接数值模拟(DNS)、雷诺平均N-S方程(RANS)和大涡模拟(LES)三种。从结构工程实践的角度看，DNS与LES方法计算量巨大，限于计算机条件的约束，不适用于工程应用，现有数值模拟一般采用基于时间平均的雷诺平均方(RANS)法[19]。 RANS 方法中湍流模型的选取是数值模拟的核心问题，然而湍流模型或多或少都带有一定的经验成分，因此在实际计算过程中，需要进一步探讨湍流模型的选取对计算结果的影响。

结合实践经验，剩余设置项为：选择压力基求解器和SIMPLEC算法进行速度压力耦合，对流项采用精度较高的二阶迎风离散格式，计算域入口为速度入口，空气出口为压力出口，船舶结构表面为壁面边界条件，流域其他边界采用对称边界。

3 数值计算影响因素分析

以船舶正迎风工况为例，以经验公式计算结果为参照，对比不同网格划分形式和不同湍流模型对数值计算结果的影响。

3.1 网格划分对计算结果的影响

按照控制变量的原则，在计算过程中暂时选定湍流k-εrealizable模型。分别在相对风速为10和15 m/s下，对三套网格分别进行计算，见表3。

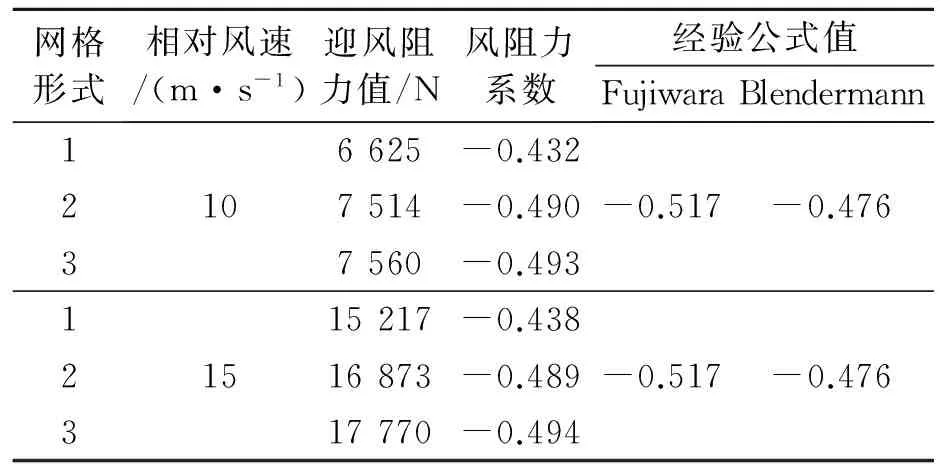
表3 三种网格形式数值计算结果对比

由表3可以看出，网格1的划分比较粗糙，且流域偏小，导致计算结果偏差较大，而网格2和3计算结果和经验公式比较接近，在相对风速发生变化时，风阻力系数基本保持稳定。

3.2 湍流模型对计算结果的影响

基于RANS方法的湍流模型包括：①Spalart-Allmaras 模型；②k-ω模型，包括k-ωRealizable、k-ωStandard和k-ωRNG；③k-ω模型，包括k-ωRealizable和SSTk-ω；④雷诺应力模型(RSM)。

以网格2为算例，在相对风速为10 m/s时，计算结果见表4。

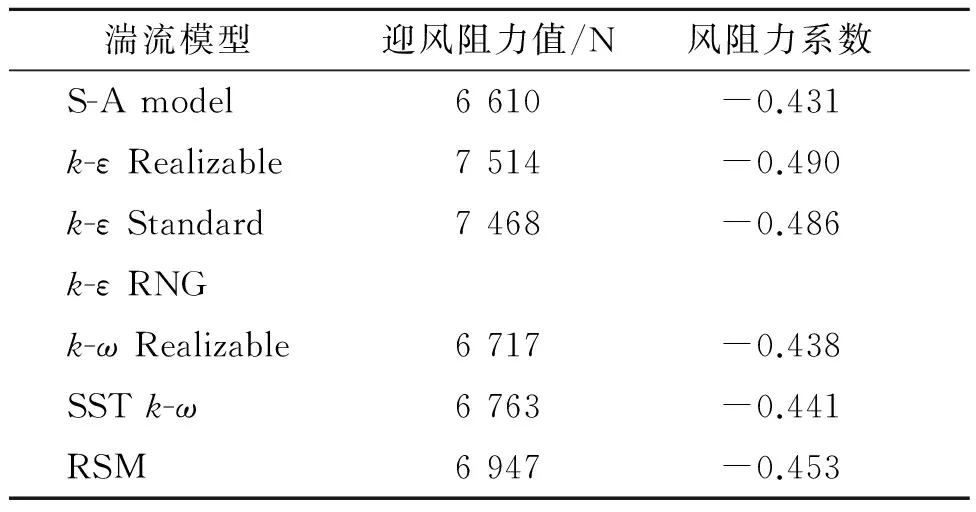
表4 三种湍流模型计算结果对比

由以上对基于RANS的7种湍流模型进行计算对比后可以看出，k-εRealizable模型与k-εStandard模型的计算结果与经验值最为接近，且两种模型的收敛时间较其余几种收敛时间短，效果最好；而k-ε模型中，RNG模型在计算阻力值时出现振荡，Realizable和Standard模型的计算结果相差很小，但前者收敛时间短，收敛性更好，更具参考价值。根据上述分析与对比，为缩短计算时间，提高数值模拟的准确度，网格划分选择第2种设置形式，湍流模型选择k-εRealizable模型。

4 不同风向角下计算结果对比及分析

4.1 CFD计算流场分布

对船模在0°～180°，间隔角为10°的不同风向角下进行数值计算，从中选取θ=0°、60°、90°和120°共4个风向角下的计算结果，其压力云图和流场分布见图4～7。当船舶行驶方向与相对风向相反，即θ=0°时，船舶流场流线变化均匀且分布较为对称，见图4。

图4 0°风向角下的流线和压力分布

当船舶行驶方向与相对风向的夹角θ=60°和120°时，船体迎风侧和背风侧的流场分布不再对称。迎风侧的流线密集，压力大；背风侧流线稀疏，压力小。在船体艉部和艏部装有尖角部位的背风侧出现旋涡，并与其他的气流相互缠绕，见图5和图6。

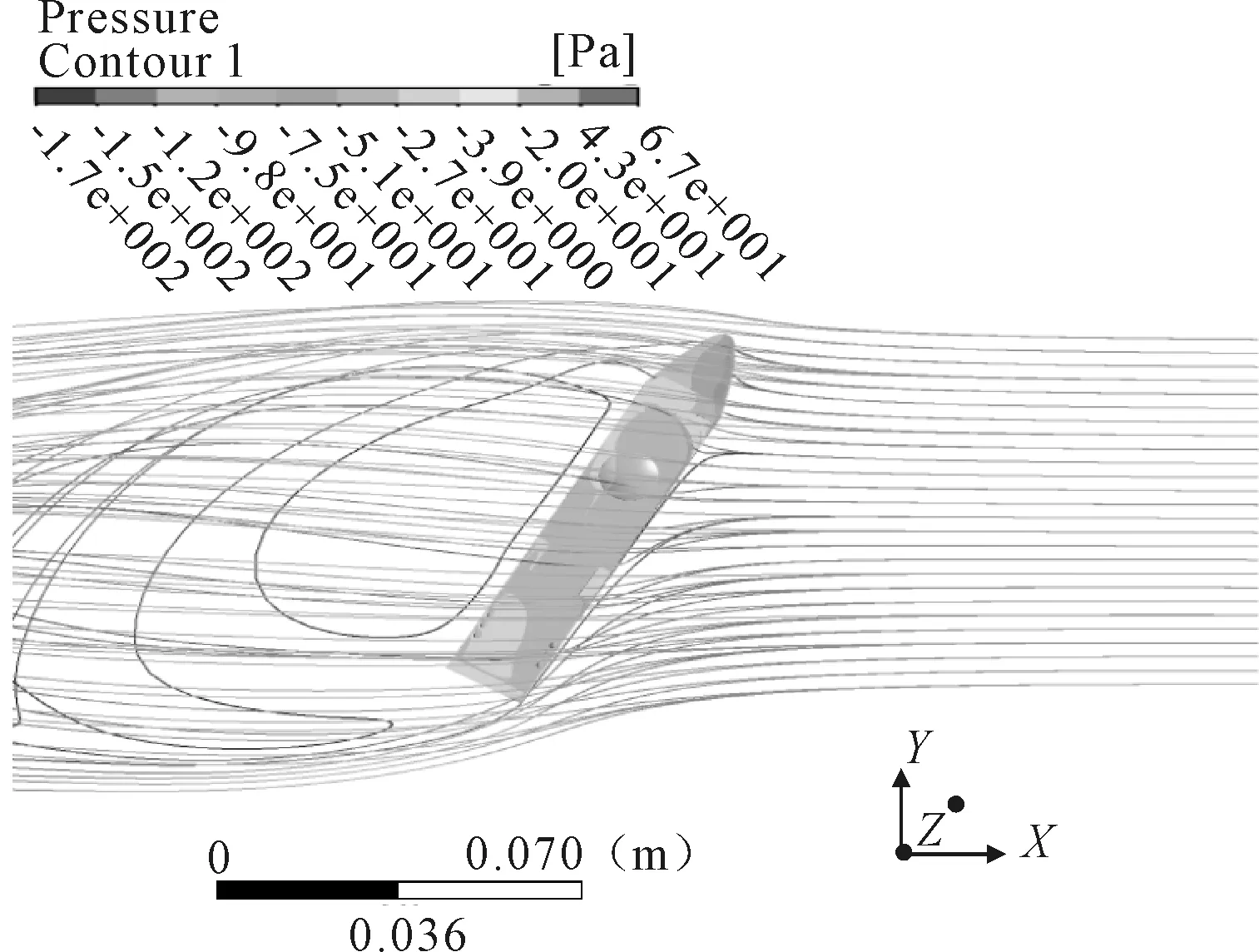
图5 60°风向角下的流线和压力分布

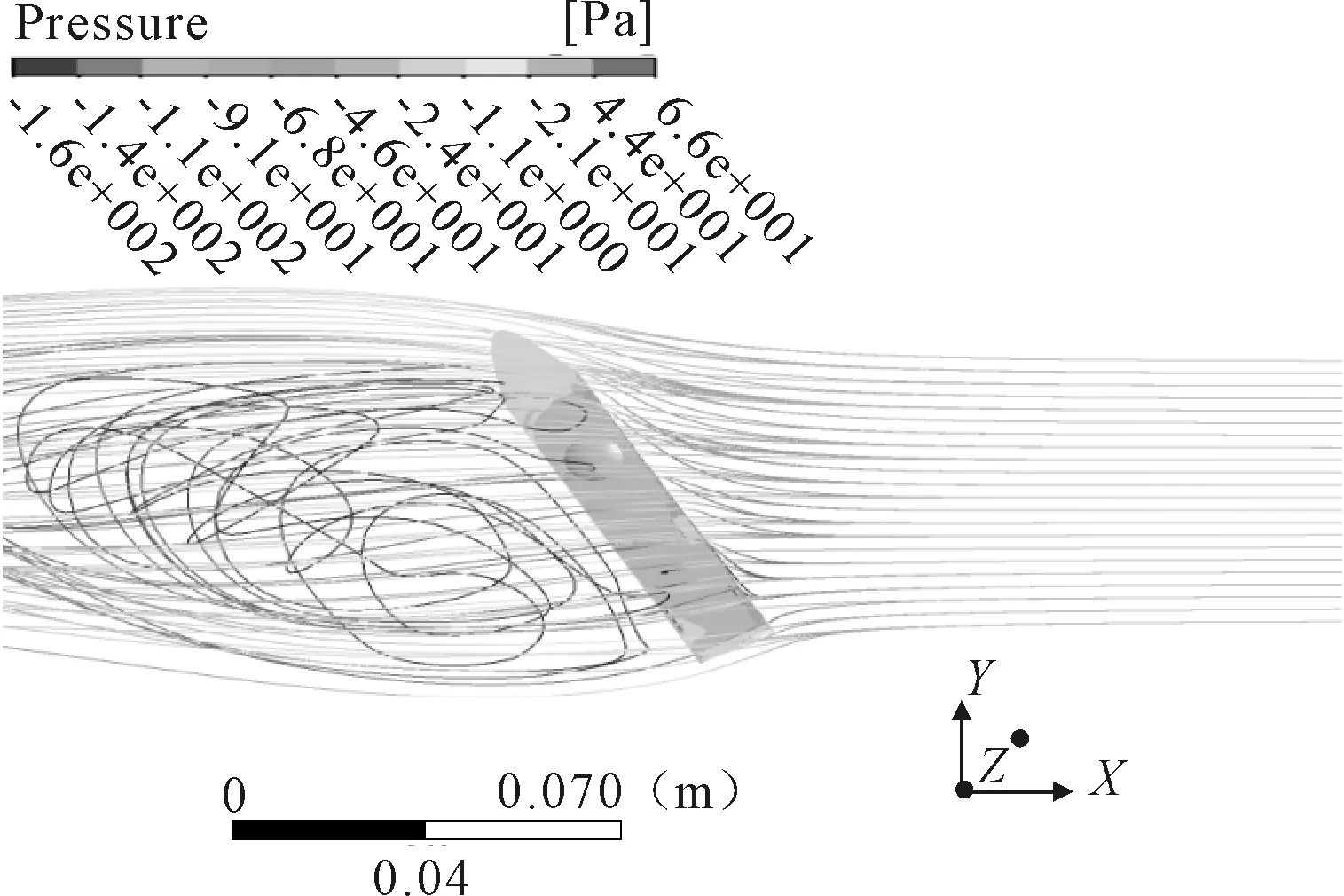
图6 120°风向角下的流线和压力分布

当船行驶方向与相对风向垂直，即θ=90°时，背风侧出现流向封闭环绕且尺寸较大的旋涡，见图7。

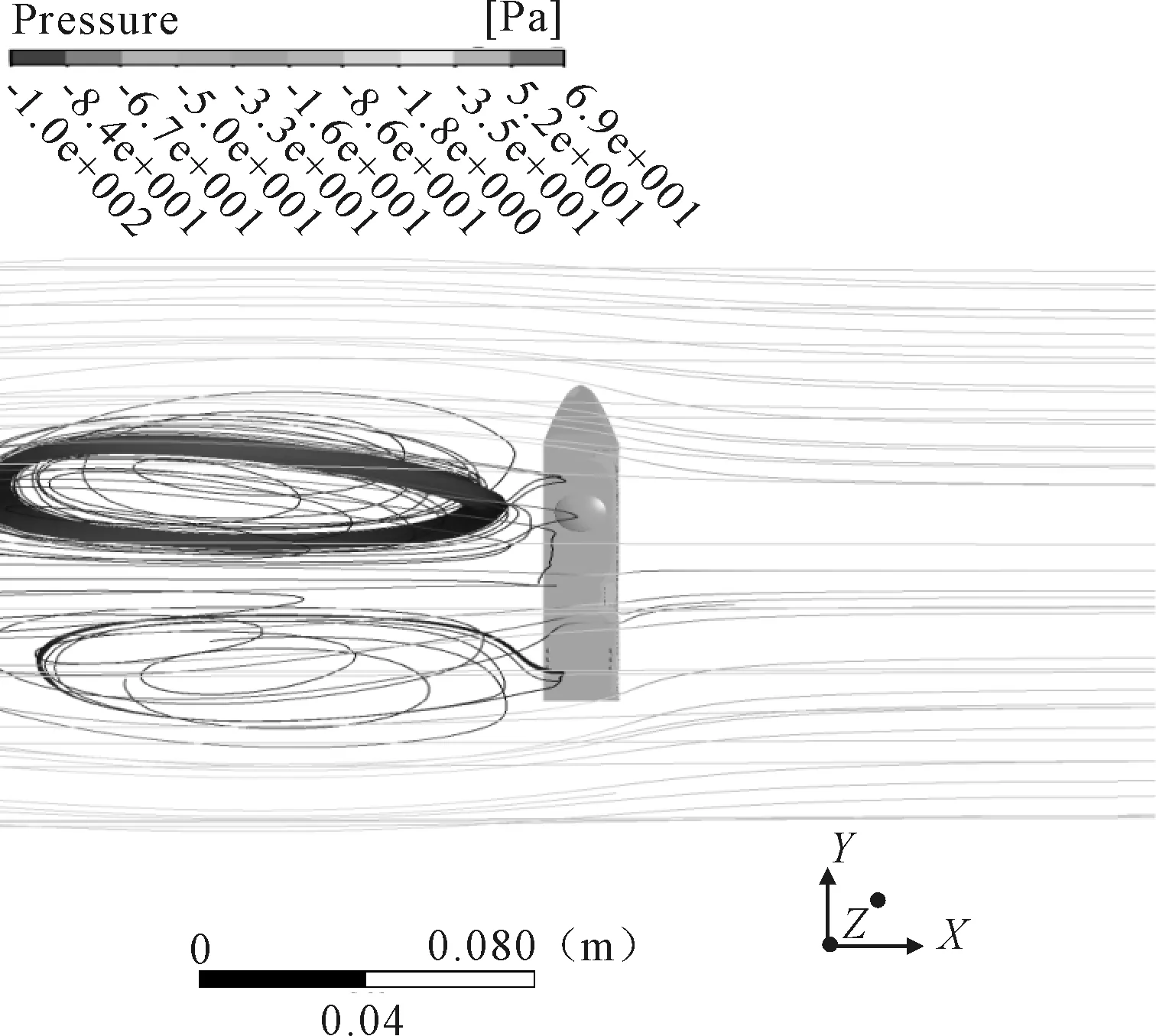
图7 90°风向角下的流线和压力分布

4.2 风载荷系数计算结果对比

将经验公式和CFD计算得到的CX、CY、CN进行对比分析，如图所示，CX随风向角的增大整体变化趋势比较凌乱，这与对象船舶艏艉结构不对称有关；CY随风向角度变化平缓，在60°和120°附近达到最大值；艏摇力矩系数CN同样变化平缓，在40°和140°附近绝对值取得最大值。

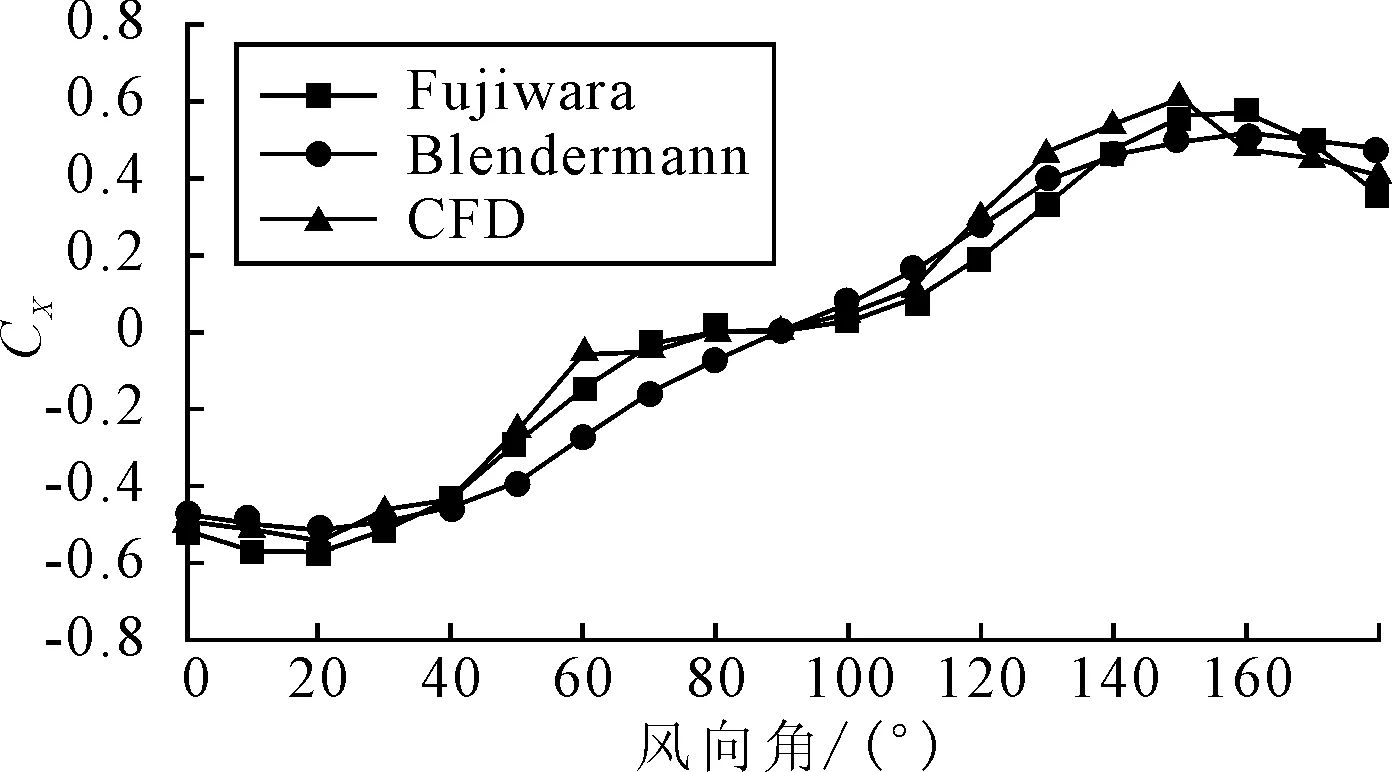
图8 纵向风载荷系数随风向角度的变化

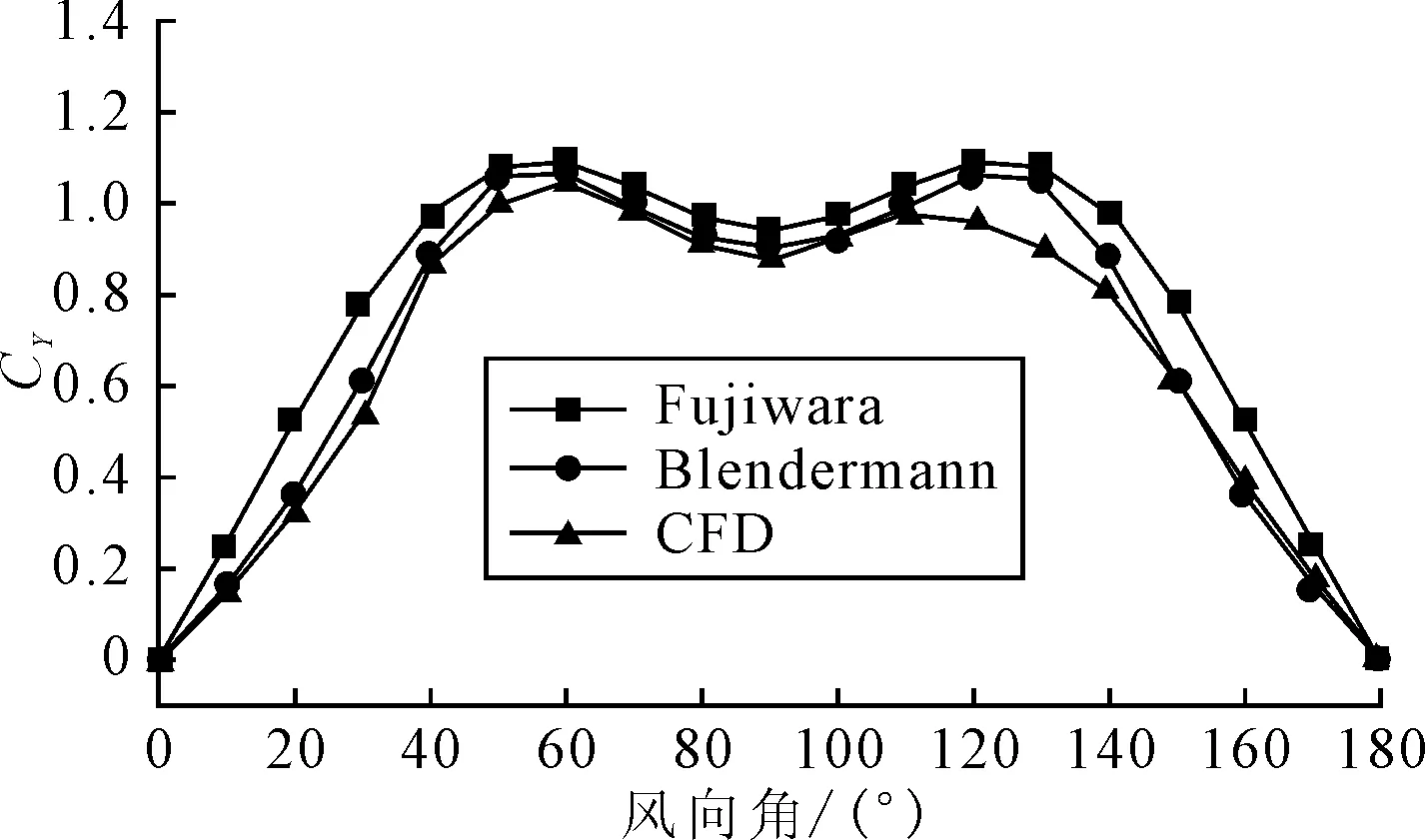
图9 横向风载荷系数随风向角度的变化

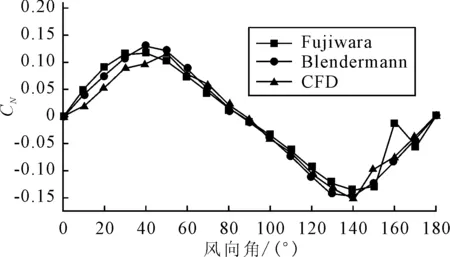
图10 艏摇力矩系数随风向角度的变化

对以上计算结果，利用欧氏距离量化经验公式与CFD计算结果间的相似程度，欧氏距离值越小表示吻合度越高。计算结果见表5。

表5 经验公式与CFD计算结果的欧氏距离

由表5可见，在计算纵向风载荷系数时，Fujiwara公式与CFD相似度最高；而在计算横向风载荷系数与艏摇力矩系数时，Blendermann方法与CFD结果相似度最高。总体来看，3种计算方法具有很好的吻合度。

5 结论

1)对不同湍流模型进行船舶风载荷系数计算，对比分析表明，k-εRealizable模型的计算结果与经验值最接近。因此在对内河游轮风阻计算中推荐采用k-εRealizable湍流模型。

2)船体上层建筑的风载荷系数随风向角变化较大，由CFD方法获得的船舶在不同风向角下的流场分布可知，风向角度及上层建筑的钝体程度对船舶背风侧的风场分布影响较大。

3)CFD计算方法与Blendermann方法和Fujiwara方法吻合良好，计算精度能满足工程实际应用要求。采用的 CFD 计算策略及网格形式可较好预报游轮风阻力。

[1] Marine Environment Protection Committee. Report of the Marine Environment Protection Committee on Its Sixty-Second Session [R]. London: IMO,2011.

[2] 陈前昆,严新平,尹奇志,等.基于EEOI的内河船舶航速优化研究[J].交通信息与安全,2014,32(4)：87-91.

[3] 庄亚龙,杨彦杰.CFD在船舶行业中的发展和应用[J].科技创新与应用,2013(32):12.

[4] 张 峥.船舶海上环境力载荷和稳态动力定位能力研究[D].上海:上海交通大学,2012.

[5] 魏锦芳,尹尽勇,缪泉明.船舶在风浪中的失速预报方法研究[C]∥第九届全国水动力学学术会议暨第二十二届全国水动力学研讨会论文集.成都,北京：海洋出版社,2009.

[6] Ohmatsu S, Takai R, Sato H. On the wind and current forces acting on a very large floating structure[J]. Journal of Offshore Mechanics and Arctic Engineering, 1997,119(1):8-13.

[7] T S Lee, H T Low. Wind effects on offshore platforms: A wind tunnel model study[C]∥The Third International Offshore and Polar Engineering Conference. Singapore. 1993:6-11.

[8] 林 一，胡安康，熊 飞．自升式平台风载荷数值模拟与实验研究[J].水动力学研究与进展，2012:27(2):208-214.

[9] Ahmad K, Khare M, Chaudhry K K. Wind tunnel simulation studies on dispersion at urban street canyons and intersections:a review[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2005,93(9):697-717.

[10] Whale J, Anderson C G, Bareiss R, et al. An experimental and numerical study of the vortex structure in the wake of a wind turbine[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2000,84(1):1-21.

[11] Viola I M. Downwind sail aerodynamics: a CFD investigation with high grid resolution[J]. Ocean engineering, 2009,36(12):974-984.

[12] 张金鹏.大型集装箱船风载荷理论分析及计算[D].哈尔滨:哈尔滨工程大学,2012.

[13] 蔡文山,董国祥,杨春勤,等.船舶风载荷数值计算及风洞试验[C]∥第二十五届全国水动力学研讨会暨第十二届全国水动力学学术会议文集,浙江舟山,北京：海洋出版社,2013.

[14] Andersen IMV. Wind loads on post-panamax container ship[J]. Ocean Engineering, 2013:58(2):115-134.

[15] Fujiwara T, Ueno M, Nimura T. An estimation method of wind forces and moments acting on ships[C]∥Proceedings of the Mini Symposium on Prediction of Ship Manoeuvring Performance. 2001:83-92..

[16] Blendermann W. Wind loads on moored and manoeuvring vessels[J].OMAE, Offshore Technology,1993(1):183-189.

[17] Blendermann W. Parameter identification of wind loads on ships[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1994(2):339-351.

[18] Blendermann W. Estimation of wind loads on ships in wind with a strong gradient, offshore technology[J].1995(1):271-277.

[19] 温 正,石良辰,任毅如.流体计算应用教程[M].北京:清华大学出版社,2009.

Research on Wind Load Coefficients of an Inland Cruise Ship Based on CFD

CHEN Qian-kun1a,b, YIN Qi-zhi1a,b, FAN Ai-long1a,b, YAN Xin-ping1a,b, ZHENG Jie2, WANG Rui1c

(1a. Reliability Engineering Institute, School of Energy and Power Engineering;b. Key Laboratory of Marine Power Engineering and Technology (Ministry of Communications);c. School of Energy and Power Engineering; Wuhan University of Technology, Wuhan 430063, China;2. Chongqing Harbor and Waterway Management Bureau, Chongqing 401320, China)

In order to obtain the accurate calculation methods of wind load coefficient and its distribution under different wind direction angle, an inland cruise ship is chosen as a research object whose wind field pressure distribution and wind load coefficients are simulated by means of computational fluid dynamics, and the numerical results are compared with those of Fujiware and Blendermann method. The results show that the model ofκ-εRealizable has a high accuracy; wind load coefficients vary greatly with the coming wind angles; and the method of numerical computation adopted in this paper can accurately calculate the wind load of the inland cruise ship.

Inland ship; wind load coefficients; numerical simulation; flow field analysis

10.3963/j.issn.1671-7953.2015.06.005

2015-06-30

国家自然科学基金(51279149)；高等学校博士学科点专项科研基金优先发展领域课题(20120143130002)；武汉理工在大学自主创新研究基金项目(2015ND-B1-08)

陈前昆(1989-)，男，硕士生

U633.2

A

1671-7953(2015)06-0018-05

修回日期：2015-07-10

研究方向:船舶风阻

E-mail: qkchen_whut@163.com