角接触轴承寿命的灰色预测分析
朱云, 冯进, 卜永波, 齐列锋
(长江大学机械工程学院,湖北荆州434023)
0 引言
随着石油机械设备的要求越来越高,对钻具中角接触轴承的稳定性也提出了更高要求,要求其在实际使用中不会发生提早失效的现象。但是目前因受制于测量成本和某些因素的限制,在轴承具体的失效数据很少的情况下无法做到概率分布的建立和确认。在以往的疲劳寿命测试中,根据Weibull distribution参数,如果对仅有的少量的几组轴承试验数据做统计,结果必然存在一些偏差。相比而言,灰色系统理论需要的数据较少,此外该理论对数据是否服从何种概论分布也无严格的要求。故该理论在轴承的寿命分析中运用无疑是一个有益的探索。
1 灰色预测分析
灰色系统是一门研究信息部分清楚、部分不清楚并带有不确定性现象的应用数学学科。它以“部分信息已知,部分信息未知”的“小样本”、“贫信息”不确定性系统为研究对象,主要通过对“部分已知信息的生成、开发,提取有价值的信息,实现对系统运行行为、演化规律的正确描述和有效监控。在灰色理论中,最早提出的预测模型是灰色GM(1,1)模型,目前在灰色系统理论中应用最广。
2 灰色系统理论模型的建立
灰色系统理论通过有限的数据,在这看似表象无关的、离乱的数据中获取内在的某在规律。即在现有数据的基础上去寻找现实数据的规律。我们通常先确定灰色序列,然后进行确定近似微分方程模型,也就是灰建模。
最常用于灰色预测的GM(1,1)模型,它是一个基于生成系列的只含有一个变量的一阶灰色微分方程。这一模型被广泛应用于各种科学研究。GM(1,1)模型微分方程为:
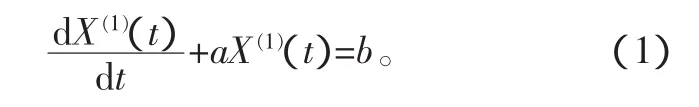
式中:a为发展系数;b为灰作用量。它们的值可以通过角接触轴承磨损寿命数据的小样本生成序列,利用最小二乘法求得。它是由一个仅包含单一变量的一阶微分方程构成的模型。
设样本的原始数据序列为X(0()k)={x(0()k),k=1,2,……,n},它表示角接触轴承磨损寿命的原始数据序列。通过一次累加就可获得原始数据生成的数据序列:X(1()k)={x(1()k),k=1,2,……,n},其中:X(1()k)=(i),k=1,2,……,n,待辨识的两个参数a和b,可由最小二乘法求解确定:

根据xˆ(0)(k)=xˆ(1)(k)-xˆ(1)(k-1)做累减计算,可得原始数据的预测值:

根据所建立的模型,最近的几个数值才是较为精确并且具有实际意义的预测值,而较远的数值只能作为一种变化趋势的参考。所以,将少量的原始的试验数据建立GM(1,1)模型,然后得到一个预测的数值,并将这个得到的数值添加到原始的数据当中,并且删除最先的一个数据,然后再重复以上步骤,直到达到磨损寿命预测的数据要求。
3 角接触轴承灰色预测计算与分析
3.1 灰色预测计算结果
采用轴承为井下涡轮钻具ZCJ178D-10.00专用角接触推力轴承组,试验载荷为10 t,假设理想情况下,分载至每个轴承副的载荷为0.5 t,即试验载荷为5 000 N,轴承滚动体及内、外圈所用材料为55SiMoVA。轴承磨损失效时的循环数为表1所示。

表1 轴承磨损失效时的循环数
由试验数据得到的原始数据序列为X[0]=[3.84 3.6 3.864 3.792]T,累加生成的数据序列为 X[1]=[3.84 7.44 11.304 15.096]T。
由上述理论可知:b=3.515,a=-0.025;b/a=3.515÷-0.025=-140.6。
所以可得原始数据的预测值
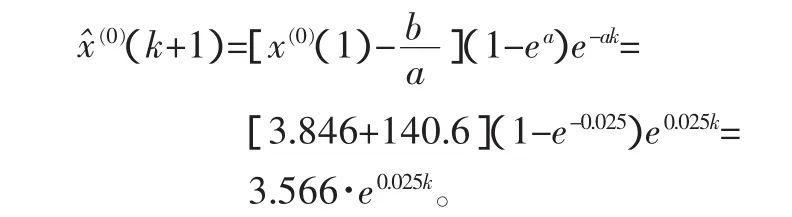
由此得出xo的预测值,如表2所示。

表2 轴承磨损寿命的实测值与预测值比较
3.2 计算结果分析
经过计算得到平均相对残差为3.285%,预测的可靠度为96.715%,其预测精度为一级。说明灰色GM(1,1)模型能够对角接触轴承的磨损寿命之后的一些数据做出预测,由此确定的有关角接触轴承寿命的分布函数,分析结果可信。
4 结论
1)灰色预测理论可以在原始实验数据不充分的情况下,通过建立GM(1,1)模型构造角接触轴承磨损寿命数据序列,解决由于实验数据不足而造成的结果偏差。
2)利用灰色预测研究方法对角接触轴承进行寿命测试,不但可以减少实验的经费,而且可以缩短试验时间。比传统的可靠性评估法更具优势。
[1] 赵迎祥,魏宗平.滚动轴承磨损寿命数据的灰色预测[J].机械制造,2010,48(11):66-67.
[2] 王长兴,夏新涛,陈龙.灰色系统理论在滚动轴承研究中的应用[J].精密制造与自动化,2007(3):12-15.
[3] 刘思峰.灰色系统理论的产生与发展[J].南京航空航天大学学报,2004,36(2):267-272.
[4] 邓聚龙.灰理论基础[M].武汉:华中科技大学出版社,2002.

