二次曲面金属幕墙褶皱优化的横向推位算法
张亚龙 , 马炫 , 蒋晓丹
(1.衢州学院 电气与信息工程学院,衢州 324000;2.西安理工大学 自动化与信息工程学院,西安 710048;3.西澳大学 电气电子与计算机工程学院,澳大利亚 珀斯 00126G)
0引 言
金属幕墙作为大型建筑外墙装饰材料近年来被广泛采用,具有保护建筑物、防腐蚀、隔噪声及美观的作用。曲面造型的金属幕墙其生产工艺比较复杂,首先是将三维曲面按照一定美观需求分割成若干个较小的曲面块,每个曲面块再由平面金属板材经过塑性冲压而成。抛物面、椭球面、球面等二次曲面是常用的基本曲面形式,复杂造型的曲面基本也由这几类曲面相贯或拼合而成。
二次曲面属于不可展曲面,也就是说由平面冲压成曲面时,褶皱的产生不可避免。而锥面和柱面可以由平面在不产生褶皱的情况下经过弯曲而成。国内外对不可展曲面成型的方法和工艺有一定研究[1-7]。解决了曲面处理相关工程的部分问题。
曲面金属幕墙由于美观装饰的需求,要求装配于建筑外表面后曲面块之间的接缝整齐均匀,对生产工艺特别是展开方法要求较高。通用展开算法[3]专门针对金属曲面幕墙,没有考虑边心距相等的要求,不适合用于曲面金属幕墙。等边心距展开方法[8]考虑了曲面展开后边界点到中心距离不变的要求,但是没有考虑褶皱分布问题,使得曲面在冲压成型过程中由于褶皱的密度不同,径向(纵向)褶皱向横向挤压,在处理曲率不对称曲面块时,边界点发生漂移,对装配的形状要求产生影响。
本文以文献[8]为研究基础,提出一种边界点的横向推位算法,计算曲面冲压时产生的褶皱横向移位量,给出边界点在褶皱移位之后的横向位置,根据横向位置可以调整纵向位置微弱变化以满足整体形状要求,使得经过冲压移位之后的形状刚好满足装配时的形状要求。
1 横向推位算法
1.1 问题描述
曲面幕墙展开要解决的问题是,给定曲面块计算对应的平面形状,使得平面形状经过冲压成型后的曲面,刚好满足曲面装配要求的接缝平滑整齐要求,从而解决目前所用的手工模胎方法带来的形状不准确需要多次返修的不便。
计算曲面对应的平面形状,首先确定曲面块的大致中心位置,以作为平面块对应的中心位置,然后计算平面形状的边界点相对于中心点的位置即可确定平面形状。因为褶皱线是径向的,我们把边界点作为褶皱线的终点,其位置分为纵向(径向)位置与横向位置。这里的纵向与横向是相对于褶皱线的纵向与横向,不是直角坐标系里的纵向与横向。文献[8]解决了边界点纵向位置,也就是边界点离中心点之间的距离。但是没有考虑边界点在横向上需要优化。本文解决第二个问题,即边界点在横向的优化位置。
1.2 边界点的纵向与横向初步位置
曲面中心点的确定比较简单。实验表明,曲面中心点无论采用几何中心的近点还是重心的近点,对计算结果的影响微乎其微,这里不做叙述。为了上下文便于理解,首先介绍等边心距展开方法[8]对边界点纵向位置的计算方法,以及横向位置的确定方式。然后介绍本文提出的横向推位算法。
1.2.1 纵向位置计算
如图1所示,曲面ABCD为给定曲面块,中心点为P。过P点做曲面的法线PQ,过PQ做平面PQME与ABCD相交于P(E,E点为曲面块的其中一个边界点。计算P(E的曲线长度,在PQ的法平面与PQME平面的相交线上取点E′,使直线距离PE′=P(E作为E点在平面上的对应点。以PQ为轴旋转平面PQME,依此与给定曲面边界点相交,计算相交线的曲线长度,即边界点与中心点P的曲线长度作为平面上边心距,可得其他边界点在平面上的纵向位置。
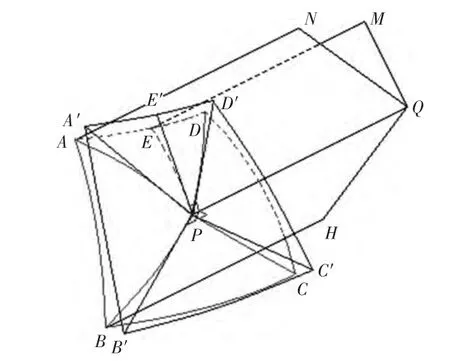
图1 曲面展开示意图
设给定曲面在三维空间的曲面方程为 F( x,y,z)=0,方程在三维坐标系的偏导数(为曲面块法线 PQ 的方向。由于P点的坐标已知,得出直线PQ的点法式方程:

则平面PQME的点法式方程为
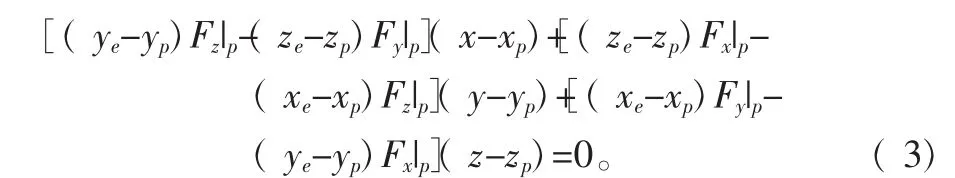
在设定边界点步长为固定值的基础上,同样的道理可以确定每个边界点在平(面上的位(置。如图1中平面PQNA 与曲面相交于曲线曲线的长度 PA′可以确定A点在展开平面的纵向位置。以此类推可以确定B点、C点以及D点的位置。然后形成如图1中曲面ABCD的展开平面形状 A′B′C′D′。
1.2.2 横向位置初步计算

以E点为基准,由式(4)得出的二面角作为展开平面中各边界点与E点的夹角,如图1中∠EPA′、∠EPB′、∠EPC′等与作为基准点E点的夹角确定了在平面上A′点、B′点、C′点的初步横向位置。展开过程中,计算曲面与平面相交的曲线长度时,如的长度,由于没有通用的数学公式,计算较为复杂。可采用曲线分段拟合的方法求解,思路为:把曲线分为若干个小段,每一段用经过两端和中点的抛物线的长度拟合代替,各小段的拟合长度累加之和即为曲线长度。
1.3 边界点的横向推位算法
上述的展开过程实际上已经确定了边界点在平面中的横向位置,但是没有考虑褶皱均匀化之后边界点在横向的移位。在得出横向移位的量度之后,可以根据曲面装配时的边心距要求,适当调整纵向长度以满足曲面装配形状要求,纵向长度的调整不是本文的研究问题,这里不做叙述。下面给出边界点横向移位量的计算方法。
如图2给定曲面块ABCD,以边界点E的横向推位计算为例,其他边界点的计算以此类推。

图2 横向推位算法示意图
计算DX在空间曲线上的积分,两积分之差即为E点横向移位量,即E点的横向移位量为
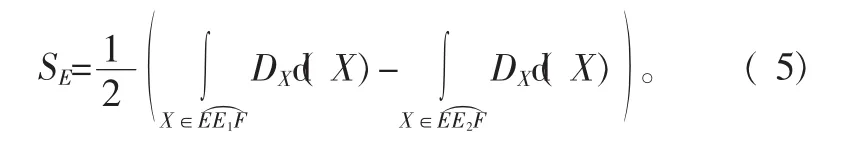
移位的方向为沿圆周的曲线方向,而不是切线方向。SE值的正负决定了移位朝E点的左边还是右边。褶皱均匀化使得边界点由褶皱密度大的地方向褶皱密度小的方向移位。
2 计算实例
给定抛物面如图3,已知抛物面方程为

其中:a=100,b=100,p=0.01,h=100。 经纬线分割后取 3 块曲面如图中阴影部分。3块曲面的参数如表1。其中曲面块1的展开图如图4。
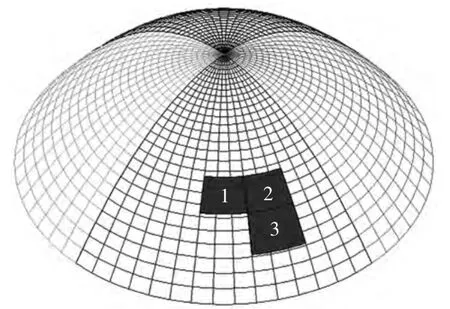
图3 抛物面曲面块

表1 曲面块参数
图4显示的曲面块1的平面展开形状似乎与曲面块的三维视图变化不大,这是由于所取的曲面块相对于整个曲面相对较小,曲率表现不明显。但在64位的计算机中计算精度非常高,可以满足刚性金属钣金装配时,接缝之间的精确预留距离,达到美观精致的效果。实际工程的曲面块划分的相对大小有可能更大或更小,当更大时曲率表现明显,展开结果与曲面的三维轮廓区别较大。
图5(a)为曲面块1展开的褶皱分布示意图,其中径向阴影线为褶皱线;图5(b)为经过褶皱横向推位后的褶皱分布对照图。可以看出褶皱经过横向推位后分布均匀,为曲面块的冲压成型过程带来了方便,可以直接冲压,经过自然延展后形成装配所需的形状及尺寸。
图4 曲面块1展开图

图5 褶皱优化对照图
3结 语
二次曲面幕墙平面展开的褶皱横向推位算法考虑了金属板材在冲压时,褶皱向密度小的方向横向推挤的形变因素;以及给出了移位量的计算方法,使得曲面在冲压成型时,褶皱可以均匀分布,简化了对冲压工艺的要求。结合等边心距展开方法[8],横向推位算法已经开发成计算机应用系统,在实际生产中应用效果良好。一方面代替了以前的手工模胎方法,使得生产效率大大提高。另一方面在解决精确计算的基础上,简化了冲压工艺,极大地提高了产品质量。
[1] 洪晴,黄翔,李泷杲,等.钣金不可展曲面展开有限元逆算法的研究与实现[ J].机械制造与自动化,2011( 2):37-39.
[2] 薛亚平,陈志伟.犀牛软件在曲面金属幕墙钣金生产中的应用研究[ J].机械设计与制造工程,2014( 4):67-70.
[3] 梁堰波,徐伟辰,李吉刚,等.基于力学模型的曲面展开通用算法[ J].计算机工程与设计,2012( 9):3539-3543.
[4] 严国彪,刘斌.一种基于能量模型的曲面展开改进算法[J].华侨大学学报:自然科学版,2011( 2):135-139.
[5] 阳波,陈金平,杨亮,等.逆向工程和二次开发技术在机翼壁板展开及建模中的应用[J].CAD/CAM与制造业信息化,2014( 9):49-53.
[6] 崔晓坤,陈明.拓扑最优的可展网格曲面放样建模[J].计算机应用,2012( 10):2798-2801.
[7] 崔晓坤,陈明.快速可展窄带曲面设计[J].计算机应用研究,2012( 10):3997-4000.
[8] 马炫,张亚龙,李生民.双曲面金属幕墙的等边心距展开方法[J].计算机工程与应用,2009(23):217-218.

