同等条件不同截面形式梁的数值计算分析

徐 莹

(河北省廊坊市大厂回族自治县职业技术教育中心，河北廊坊 065300)

0 引言

工程结构中，梁作为主要受弯构件承当上部荷载，并把荷载传给柱子或者承重墙体［1－3］。如果满足跨度相同，横截面积相同两个条件，这就意味着用的材料量是相同的。在材料量固定的前提下，如果此时所受荷载也相同，仅由于横截面积形状不同得到的力学效果也是有差异的，本文试图找到每种横截面积梁的受力特点，从力学角度解析其不同。

1 弯曲梁抗弯理论基础及模型建立基本前提

1.1 弯曲梁抗弯理论基础

由固体力学可知，弯曲梁的正应力计算公式为［4－6］:

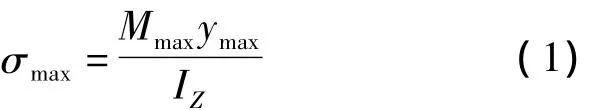
其中:σmax—弯曲梁最大正应力;Mmax—最大弯矩;IZ—惯性矩;WZ—抗弯截面系数。

通过公式(2)可知，在其它条件相同条件下，梁的抗弯性能好坏和梁的抗弯截面系数WZ密切相关，即使横截面积相同，但是不同的布置方式也会使WZ变化很大，正常情况下我们设计梁截面时候都要尽可能追求大的WZ，这样才能保证最大正应力σmax不会超过材料的容许正应力［σ］。

1.2 基本参数

本次分析采用大型通用有限元软件ANSYS，采用SOLID45单元进行数值模拟，SOLID45单元用于构造三维固体结构，单元通过8个节点来定义，每个节点有3个沿着XYZ方向的平移自由度，此单元具有塑性、蠕变、膨胀、盈利强化、大变形能力，因此非常适合用来模拟三维的钢材及混凝土［7－8］。边界条件:为了真实再现工程实际情况，因此梁的左右两端施加全方位约束。本次分析采用的基本几何和力学参数见表1。

表1 基本几何力学参数

通过表1想说明，即本文要进行数值分析的三种截面梁力学参数完全一样，跨度和横截面积也相同，这就保证了所用材料量相同，再加之所受外荷载也相同，这样等同条件下对比分析才有意义，计算的结果才有说服力。

1.3 矩形截面实心梁

矩形截面实心梁示意图如图1所示，得到的力学分析结果如图2—图5所示。其中图2是对于矩形截面实心梁的有限元网格划分;图3是计算后梁的变形图;图4是计算后的Y方向的位移云图(其中Y方向和荷载作用方向相同，即横截面竖直方向);图5是计算后得XY平面(横截面方向)的剪应力云图。

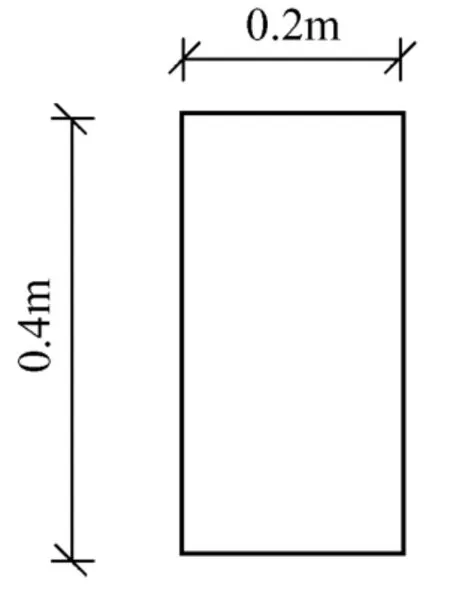
图1 矩形截面实心梁示意图

通过图3可见，该梁的最大变形是0.693×10－3m;由图3和图4可见，此最大变形发生跨中;图5表明梁的XY方向最大剪应力发生到梁的两端，大小为384157 Pa。

图2 矩形截面实心梁的有限元网格

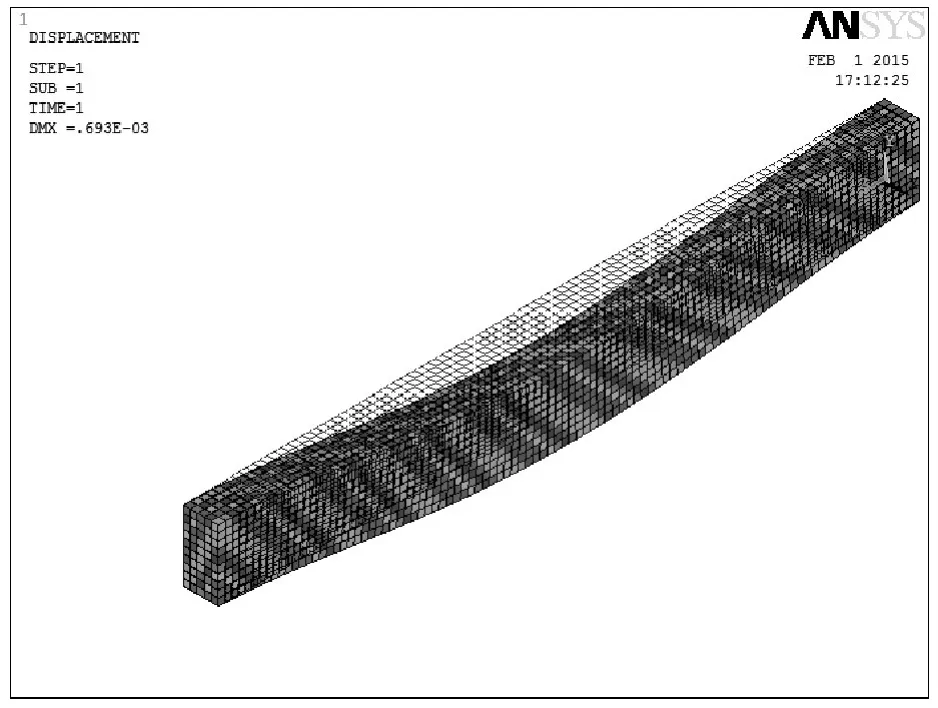
图3 矩形截面实心梁的变形图

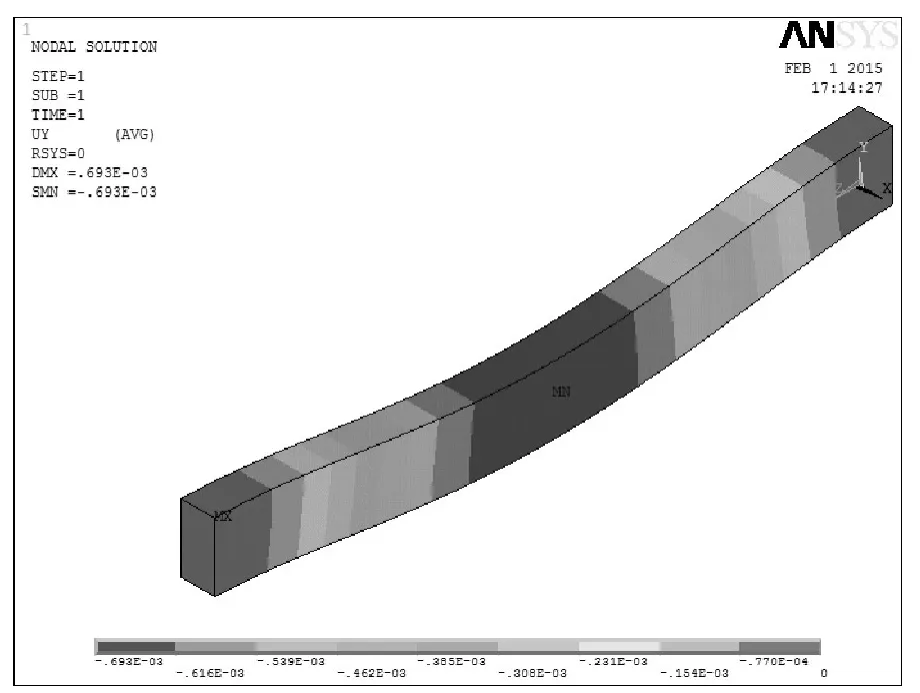
图4 矩形截面实心梁的Y方向的位移云图

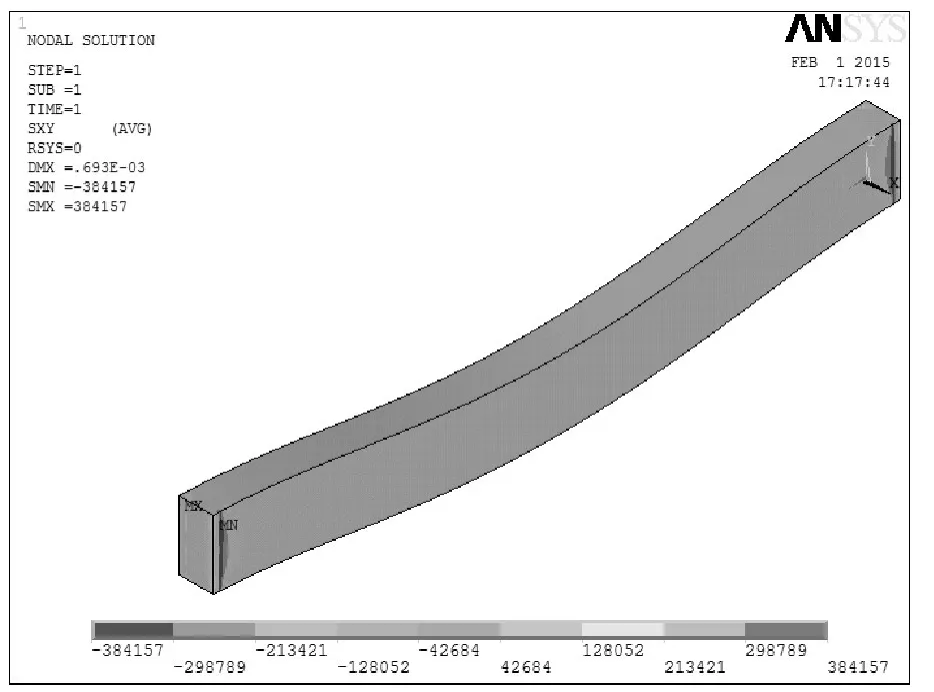
图5 矩形截面实心梁的XY平面的剪应力云图

1.4 矩形截面空心梁

矩形截面空心梁示意图如图6所示。划分的有限元网格、梁的变形图、Y方向的位移云图和XY平面的剪应力云图，依次见图7—图10。

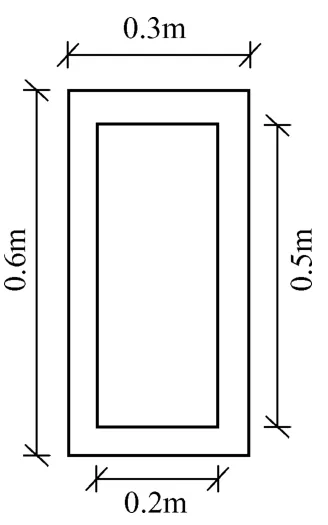
图6 矩形截面空心梁示意图

图7 矩形截面空心梁的有限元网格

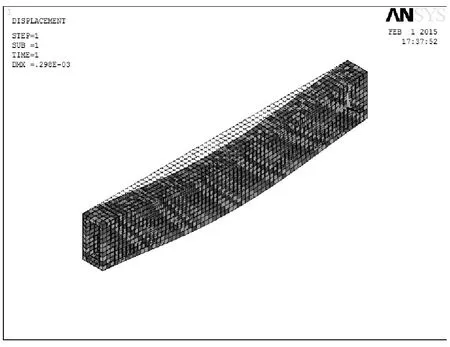
图8 矩形截面空心梁的变形图

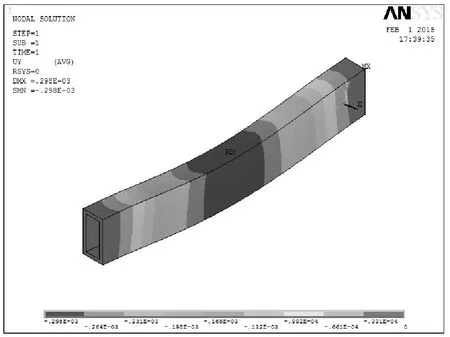
图9 矩形截面空心梁的Y方向的位移云图

通过图8和图9可知，此时梁的最大变形为0.298×10－3m;最大变形发生的位置依旧发生在跨中;最大剪应力和第一种情况对比有明显变化，其值达到了0.167×107Pa。

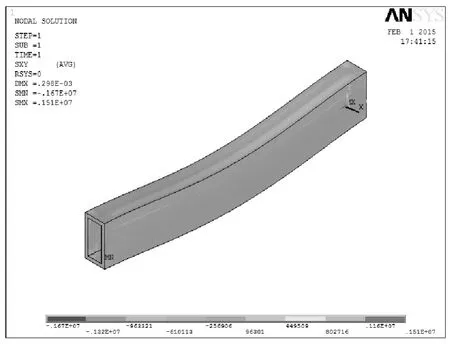
图10 矩形截面空心梁的XY平面的剪应力云图

1.5 工字型截面梁

工字型截面梁示意图如图11所示。划分的有限元网格、梁的变形图、Y方向的位移云图和XY平面的剪应力云图，分别如图 12—图 15所示。

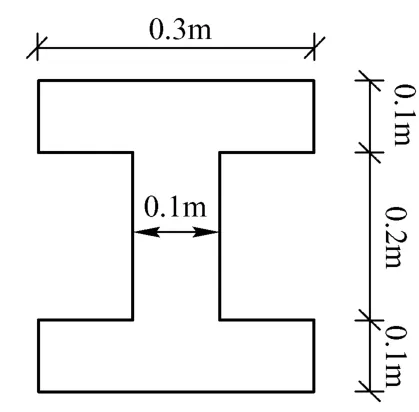
图11 矩形截面空心梁示意图

图12 工字型截面梁的有限元网格

图13 工字型截面梁的变形图

图14 工字型截面梁的Y方向的位移云图

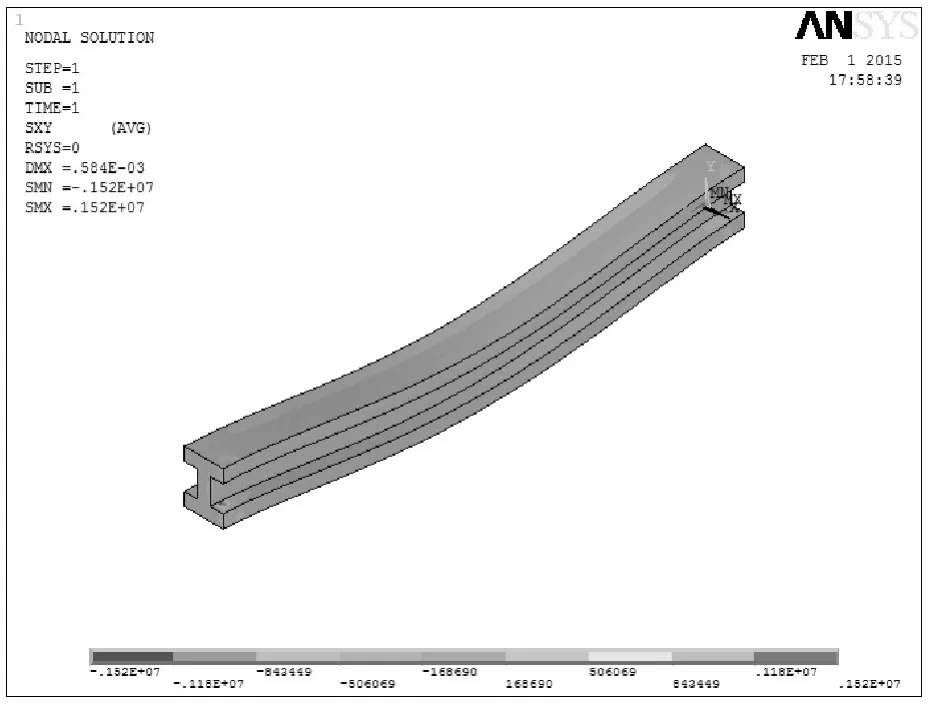
图15 工字型截面梁的XY平面的剪应力云图

通过图13和图14发现此时梁的跨中最大变形为0.584×10－3m，该数值和第一种情况下得到的相应结果接近;而此时梁的XY平面最大剪应力和第二种情况差别不大，其值为0.152×107Pa。

2 结果分析

为了便于对比分析，现把上述三种情况下得到的代表性结果列于表2中。

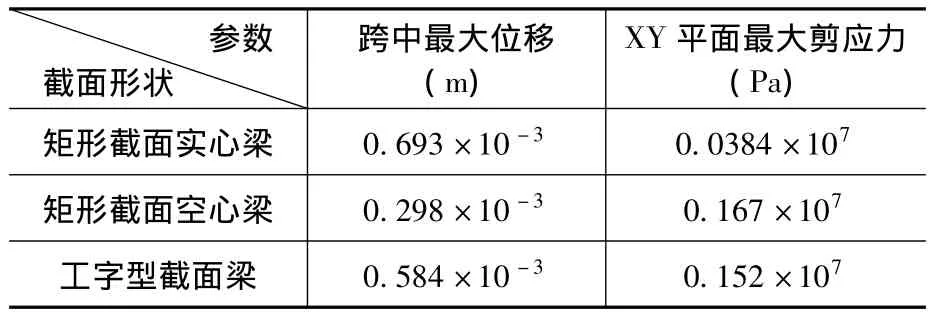
表2三种情况下结算结果汇总表

表2数据表明，在荷载、跨度、材料横截面积都相同条件下，矩形截面空心梁的最大位移比矩形截面实心梁的最大位移减少了50%以上，因此，为了减少跨中位移，即减少跨中挠度，把实心截面梁做成空心的是不错的选择，但是矩形空心截面梁的XY方向的最大剪应力却比等面积实心梁增加了4倍多，也就是说梁的端部较第一种情况相比更容易发生剪切破坏。工字型截面梁跨中最大位移和矩形截面实心梁对比跨中挠度减少了19%左右，减小的幅度有限，而XY平面剪应力同样增加了近4倍。

3 结论

在其它条件相同条件下，三种截面形式的弯曲梁具有如下优缺点:

1)矩形截面实心梁缺点是跨中挠度较大，表现出刚度不足，但是XY方向剪应力较小，不容易发生大的破坏;

2)矩形截面空心梁优点是跨中挠度减小很多，但XY方向剪应力陡增，因此此种梁切应力验算是必不可少的;

3)工字型截面梁跨中挠度有一定减少，但是XY方向最大剪应力依旧很大。

通过以上分析，我们在具体工程实践中要发挥每种截面形式梁的优缺点，做到物尽其用，发挥其优点，避免其缺点。

［1］ 薛建阳.冷弯槽钢单侧挂板墙梁的计算分析［J］.西安建筑科技大学学报，1996，28(2):157 －161.

［2］ 王慧芳.钢筋硷梁截面延性的计算分析［J］.福建建筑，2008，26(1):30 －33.

［3］ 薛飞飞.外附式平臂塔吊在超高层钢结构施工中的计算分析及应用［J］. 钢结构，2013，5(28).

［4］ 彭明.第二类T形截面独立梁的计算分析［J］.黄河水利学院学报，2007，19(3):43 －45.

［5］ Xia Jianguo.Inelastic lateral buckling behavior of steel beams［M］//Computational Methods in Engineering Advance＆Application.Singapore:World Scientific Publishing，1992:139 －144.

［6］ 钱健清.对H型钢特点的进一步分析.钢结构，2001，16(51):16－18.

［7］ 陈骥.钢结构稳定理论与设计［M］.科学出版社.2010.

［8］ 中华人民共和国国家标准.钢结构设计规范GB50017—2003［S］. 中国计划出版社，2003.