侧限高应力条件下充填体压缩变形规律分析

赵向民 孙天顺 吕文生

(北京科技大学土木与环境工程学院，北京 100083)

侧限高应力条件下充填体压缩变形规律分析

赵向民 孙天顺 吕文生

(北京科技大学土木与环境工程学院，北京 100083)

为了研究充填体在侧限高应力下的变形规律，根据现场调研结果试验室内选取灰砂比为1∶10，浓度为70%的充填体试块进行9级加载蠕变试验，得到每级加载应力下充填体的轴向变形规律。通过对充填体的压缩特性分析，得到了不同加载应力条件下充填体试块的侧限压缩系数和压缩模量；通过压缩变形应变-时间图，对侧限高应力条件下充填体试块的压缩变形机理进行分析，分析结果为新城金矿矿山充填设计及安全生产提供科学依据。

充填体 侧限 压缩特性 变形机理

随着国民经济日益发展，对矿产品需求量加大，我国浅部矿产资源日渐枯竭，矿山开采深度加大，深部开采受到高应力和岩爆等问题的困扰[1]。矿山充填采矿法能够满足矿山绿色开采要求，增加了采场稳定性，是一种安全、高效、绿色的开采技术[2-3]。目前对于充填体变形规律的试验研究，大部分限于低应力加载并且无侧向约束的情况。深部采场充填体在围岩包裹下受到高应力作用，其压缩变形规律对采场稳定性有至关重要作用[4-6]。通过试验室侧限压缩变形试验，对试验结果进行压缩特性分析，并分析压缩变形机理，研究结果对矿山充填设计和采场管理有实际指导意义。

1 侧限压缩变形试验

1.1 试验方案

侧限高应力压缩变形试验是用水泥和尾砂按照灰砂比为1∶10，浓度为70%，在圆柱形钢筒(45号不锈钢，尺寸为φ80 mm×180 mm，壁厚14 mm)中制成胶结充填体试块，在温度20 ℃、相对湿度95%的环境下养护28 d,试块的养护与压缩试验均在侧限钢筒中进行[7]。钢筒的侧限作用主要表现在压缩试验进行时充填试块只发生纵向变形而无横向变形，即发生一维压缩变形。

试验采用RLW-3000微机控制岩石剪切蠕变试验机，采用阶梯式分级加载每级恒载的方式，分级加载的载荷值分别为0.5 、1 、2 、4 、6 、9、15、22 、32 MPa。

充填体试块在侧限高应力条件下完成压缩变形之后，对试块进行烘干处理[7]。105～110 ℃恒温下烘干48 h后，取出试块，在密封条件下放置3～4 h，试块温度降低到室温之后用电子秤称重，用千分尺测量试块直径和高度。

1.2 试验结果

对充填体试块在侧限条件下进行逐级加载，试块发生轴向一维压缩，变形数据如表1所示。

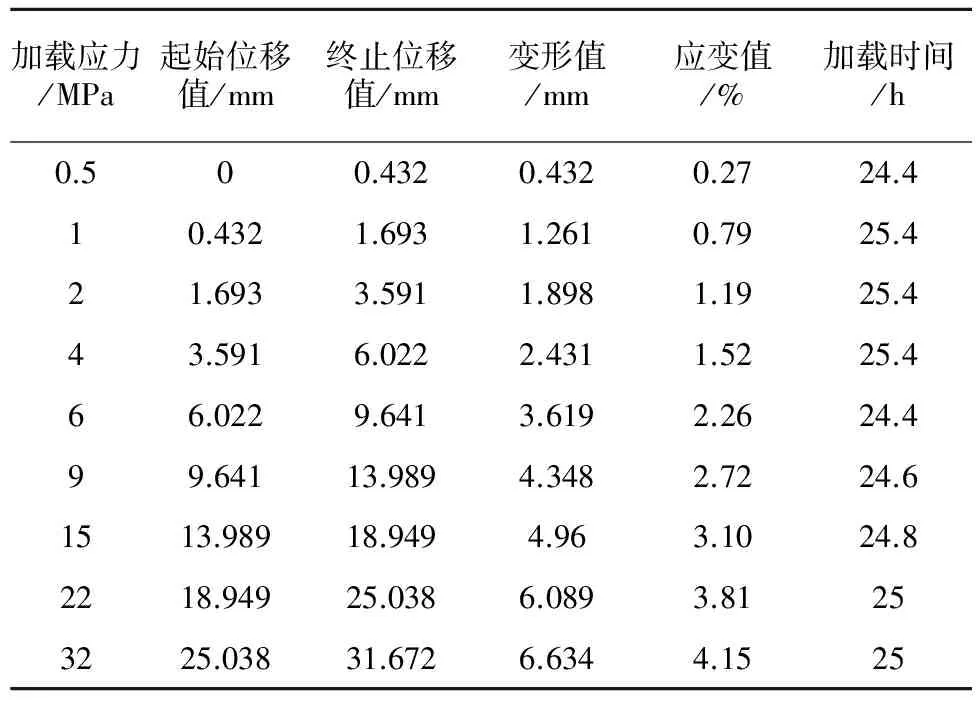
表1 侧限高应力充填体试块压缩变形数据统计表

随着加载应力逐级变大，每一级载荷对应的轴向变形值和应变值也逐渐变大；加载到最后一级32 MPa时，终止位移达到31.672 mm，是充填体试块起始高度的19.8%。

充填体试块受压并烘干后质量、尺寸会发生相应变化，结果如表2所示。

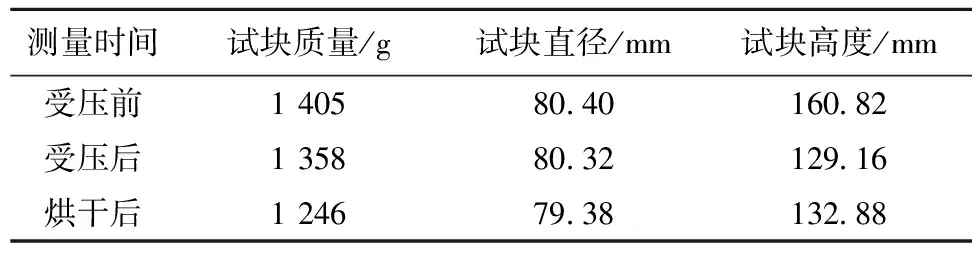
表2 充填体试块质量及尺寸数据统计表

受压后试块质量减少，主要是由于受压过程中试块完成固结与蠕变变形，试块孔隙中的空气和水排出；受压前后，由于侧限钢筒的限制，试块主要发生竖向变形，而直径基本不变。

烘干后试块质量的减少主要由于充填体颗粒物中所含水分受热蒸发，水蒸气沿试块孔隙排出，会对空隙产生膨胀扩容作用，充填体颗粒受热也会膨胀，这2种作用在宏观上表现为侧限条件下充填试块高度的增加。

2 压缩特性分析

充填体试块的初始孔隙比[8]

(1)

式中，Gs为充填体颗粒的比重；w0为试样的初始含水量；γ为初始重度；γw为水的重度，取9.81 kN/m3。

含水量计算公式为

由烘干试验可知，试块中含水质量mw=159 g,固体颗粒物质量m0=1 246 g,因此w0=12.8%；初始重度γ=W/V,试样的重力W=13.769 N,试样的体积V=8.04×10-4m3；根据新城金矿分级尾砂和水泥的密度以及充填体试块中2种材料的质量计算试块的比重为Gs=2.62，初始孔隙比e0=0.69。

2.1 孔隙比变化规律

侧限压缩试验试块轴向位移与孔隙比关系[8]，

(2)

式中，ΔHi为轴向位移；H0为初始高度。

由公式(2)求得最终孔隙比ei=0.36,得出充填体试块在侧限高应力下的e-lgt曲线图见图1。

图1 充填体试块在侧限高应力条件下的e-lgt曲线图

对图1中数据进行线性拟合，拟合函数为

e=algt+b，

式中,t为压缩时间,min；a、b为拟合系数，见表3。

表3 各级载荷作用下孔隙比随时间变化拟合结果

每一级载荷加载过程中，随加载时间的增加，充填体试块的孔隙比不断减小；随加载应力的增加，孔隙比变化幅度逐渐变大，拟合系数a的绝对值随载荷增加而变大。充填体内部孔隙中的水和气体会在轴向载荷作用下逐渐排出，充填体产生固结变形；在较高应力条件下，随着孔隙的压缩，充填体颗粒之间接触更加紧密，颗粒之间发生相对滑移，高应力使得颗粒间的挤压速度加快，孔隙比下降速度增加。

2.2 压缩系数和压缩模量

利用上述公式(2)可以计算每级载荷Δp作用下轴向变形达到稳定时的孔隙比e。压缩系数α=Δp/Δe，在完全侧限条件下，试块的压缩模量Es=(1+e1)/α。由此计算各级载荷作用下充填体试块侧限条件下的压缩系数α和压缩模量Es。计算结果如表4所示。

表4 充填体的侧限压缩系数与压缩模量

侧限条件下，新城金矿灰砂比为1∶10的尾砂胶结充填体的压缩系数为0.008 0～0.027 5 MPa-1，压缩模量为61.4～210.9 MPa；根据新城金矿相关地质资料，其开采深度已经达到800～1 000 m，综合应力达到25 MPa[9-10]，充填体侧限压缩系数应为0.008 0～0.008 9 MPa-1，压缩模量为189.8～210.9 MPa。土体的压缩系数一般为0.1～0.5 MPa-1，尾砂胶结充填体的压缩性能比土体低。对压缩系数和压缩模量随加载应力变化进行回归分析，结果如图2和图3所示。

图2 压缩系数回归分析图

3 压缩变形机理分析

根据侧限高应力下充填体压缩变形试验数据，得到充填体在连续加载(每一级应力长时间恒载)的条件下应变-时间曲线图，如图4所示。

图4 充填体侧限压缩应变与时间关系示意

由图4可知，充填体在侧限条件下每一级载荷作用初期，变形随时间增长较快，且变形速率逐渐减小，大部分变形会发生在每一级载荷加载初期，后期只发生较小变形。在加载应力9 MPa之前，充填体后期变形趋于稳定[11-12]，整个过程符合衰减蠕变；在9 MPa之后，充填体前期变形符合衰减蠕变，后期变形随时间延长而线性增加，符合稳定蠕变。对9 MPa之后充填体稳定蠕变过程应变随时间变化函数进行线性拟合，拟合直线斜率分别为15 MPa时，0.000 3；22 MPa时，0.000 4；32 MPa时，0.000 5。加载应力越大，稳定蠕变速率越快。

充填体在侧限高应力压缩过程中，当应力较低时(<9 MPa)，孔隙压力逐渐减小，固体颗粒相互靠近，发生固结变形,压缩变形主要包括瞬时的和衰减的变形；当应力较高时(>9 MPa)，充填体内部孔隙继续收缩，有效应力不断增加，充填体颗粒相互挤压，发生蠕变变形，主要包括瞬时的、衰减的和黏塑性变形，且应力越大，蠕变变形速度越快，充填体的黏塑性越明显。

4 结 论

(1)侧限高应力下充填体孔隙比e与压缩时间t符合对数函数关系e=algt+b,每一级载荷过程中，充填体试块初期变形快速，后期变形趋于稳定。通过计算，得到了各级加载应力下的压缩系数和压缩模量数值，压缩系数和压缩模量与加载应力都满足对数函数关系。

(2)新城金矿充填体侧限压缩变形过程中，在较低应力下(<9 MPa)，主要发生固结变形，包括瞬时的和衰减的变形；较高应力下(>9 MPa)，主要为蠕变变形，包括瞬时的、衰减的和黏塑性变形，且应力越大，蠕变变形速度越快，充填体的黏塑性越明显。

(3)采场充填结束后，应加强管理，防止因充填体压缩变形较大而使采场失稳，充填体压缩变形稳定后，能够对采场起到稳定的支撑作用。新城金矿现有开采条件下，充填体侧限压缩系数为0.008 0～0.008 9 MPa-1，压缩模量为189.8～210.9 MPa，其压缩性能比土体低。

[1] 王新民，肖卫国，张钦礼．深井矿山充填理论与技术[M]．长沙：中南大学出版社，2005． Wang Xinmin，Xiao Weiguo，Zhang Qinli.Filling Theory and Technology of Deep Mine[M].Changsha:Central South University Press,2005.

[2] 赵 勇，汪德浩．侯庄矿胶结充填工艺探索[J]．金属矿山，2013(3)：56-58． Zhao Yong，Wang Dehao.Exploration of the cemented filling process in Houzhuang Mine[J].Metal Mine，2013(3):56-58.

[3] 周爱民，古德生．基于工业生态学的矿山充填模式[J]．中南大学学报：自然科学版，2004，35(3)：468-472. Zhou Aimin，Gu Desheng.Mine-filling model based on industrial ecology[J].Journal of Central South University：Science and Technology，2004,35(3):468-472.

[4] 毛彦鑫，丁凌霄，冯朝朝．水砂充填采矿中采场内充填体渗流问题研究[J]．金属矿山，2013(8)：26-30． Mao Yanxin，Ding Lingxiao，Feng Chaochao.Study on permeability problems of filling in the sandfill mining stope[J].Metal Mine，2013(8):26-30.

[5] 郭 力，何朋立．采空区充填效果的随机规律研究[J]．金属矿山，2013(4)：36-38. Guo Li，He Pengli.Study on the stochastic law of gob stowing effect[J].Metal Mine，2013(4):36-38.

[6] 王新民，古德生，张钦礼．深井矿山充填理论与管道输送技术[M]．长沙：中南大学出版社，2010：69-75． Wang Xinmin，Gu Desheng，Zhang Qinli.Deep Mine Filling Theory and Pipeline Technology[M].Changsha:Central South University Press，2010：69-75．

[7] 中华人民共和国水利部．GB/T 50123—1999土工试验方法标准[S]．北京：中国标准出版社，2002. Ministry of Water Resources of People′s Republic of China.GB/T 50123-1999 Standard for Soil Test Method[S].Beijing:China Standard Press，2002.

[8] 赵成刚，白 冰，王云霞．土力学原理[M]．北京：清华大学出版社，2004：135-144． Zhao Chenggang，Bai Bing，Wang Yunxia.The Principles of Soil Mechanics [M].Beijing:Tsinghua University Press，2004:135-144.

[9] 刘 杰，徐曾和，赵东兴，等．新城金矿采场地压活动规律及支护技术研究[J]．金属矿山，2013(5)：18-21. Liu Jie，Xu Zenghe，Zhao Dongxing，et al.The law of ground pressure activities and research on supporting technology in Xincheng Gold Mine [J].Metal Mine，2013(5):18-21.

[10] 张大磊．新城金矿-580 m中段采场地压与开采方式优化研究[D]．北京：北京科技大学，2009． Zhang Dalei.The Research on Ground Pressure and Optimization of Mining of -580 m Middle Stope in Xincheng Gold Mine [D].Beijing:University of Science and Technology Beijing，2009.

[11] 范广勤．岩土工程流变力学[M]．北京：煤炭工业出版社，1993． Fan Guangqin.Geotechnical Engineering Rheological [M].Beijing:Coal Industry Press，1993.

[12] 孙 钧．岩土材料流变及其工程应用[M]．北京：中国建筑工业出版社，1999． Sun Jun.Evolution of Geomaterials and Engineering Applications[M].Beijing:China Building Industry Press,1999.

(责任编辑 石海林)

Compression Deformation Analysis of Backfill Under High Stress and Lateral Restraint

Zhao Xiangmin Sun Tianshun Lu Wensheng

(SchoolofCivilandEnvironmentEngineeringSchool，UniversityofScienceandTechnologyBeijing，Beijing100083，China)

In order to study the deformation law of backfill under high stress and lateral restraint，according to the site survey results，nine-load creep experiments on the backfill with the gray-sand ratio of 1∶10 and a concentration of 70% are carried out.Axial deformation law of backfill is obtained under each level of load stress.Compression characteristic analysis of backfill is made to get the variation of compression factor and compression modulus under different loading stresses.Through the compression strain-time diagram，the compression deformation mechanism of backfill under high stress and lateral restraint is drawn.The results provide a scientific basis for the filling design and production safety in Xincheng Gold Mine.

Backfill，Lateral restraint，Compression characteristic，Deformation mechanism

2014-12-18

“十二五”国家科技支撑计划项目(编号：2012BAB08B01)。

赵向民(1966—)，男，博士研究生。

TD853.34

A

1001-1250(2015)-02-032-04