基于稀疏地图坐标的智能车导航路径生成与优化

王任栋，章永进，徐友春，马育林

(1.军事交通学院研究生管理大队，天津300161;2.军事交通学院军用车辆系，天津300161)

电子地图的精确导航是使智能车在复杂的道 路环境中快速准确地到达指定地点的重要条件［1］，是无人驾驶技术的难点之一，也是热点之一。目前常用的方法有两种:一种是基于高精度驾驶地图的导航方法;另一种是基于现有常规电子地图的导航方法。

Google、Benz等公司智能车研发团队采用的就是基于高精度驾驶地图的导航方法。这种方法中高精度驾驶地图的构建是该方法实现的关键，分为数据采集、数据处理和道路建模3个步骤。首先使用激光雷达、摄像头、GPS接收机、惯导等传感器进行道路环境数据的采集，然后对数据进行提取、融合等处理，最后通过道路及环境建模的方式生成地图。该地图含有丰富的道路环境信息，不但可以为智能车进行精确导航，还实现了智能车的高精度定位［2－3］。但由于需事先进行大量的数据采集、处理并进行地图构建，随着地图覆盖范围的扩大，其工作量、耗时、成本以及所需的存储空间都会大大增加。Kichun等［4］提出一种对高精度地图导航数据进行精简的方法，通过一种B样条曲线的逐渐修正算法，将车辆行驶的历史轨迹用很少的数据表示出来，降低了地图存储的数据量。但该方法依然需事先驾车进行数据采集，且仅适用于与采集车行驶特性相近的智能车。

与基于高精度驾驶地图的导航方法相比，基于现有常规电子地图的导航方法具有成本低、覆盖范围广、路网完整、数据结构简单、占用存储空间少等优点，已经可以为有人驾驶汽车提供良好的导航服务。但由于其路网数据稀疏，难以直接应用于面向无人驾驶的智能车导航。针对该问题，本文提出一种基于现有地图稀疏路网数据的导航路径生成及优化方法。

1 算法基本理论

1.1 导航路径生成算法

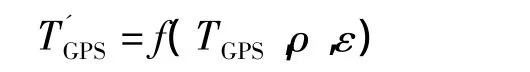
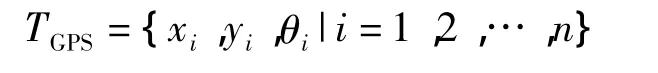
式中:xi、yi为数据点的经纬度坐标;θi为智能车在该点的行驶方向，且

1.2 导航路径优化算法

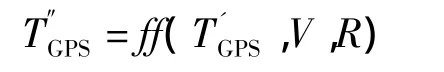
其中

式中:vr为车辆的最小转弯半径;vd为车身宽度。

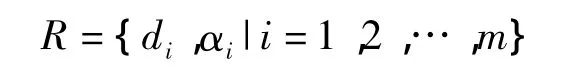
式中:di为路段的宽度;αi为路段li与li+1的夹角，由li与li+1的原始路网数据计算得到。

2 导航路径的生成

本文使用规划的路径路网数据模型为基于离散点连线的折线模型，该模型的基本要素为道路节点和路段折线。节点是描述路网结构的特征点，包括道路的起点、终点、曲率变化点、道路交叉点以及一些特殊位置点，位于由同向车道组成道路的中心线上。路段折线由节点依次连接而成，同一道路中同向行驶的多条车道用一条折线表示，不同道路或同一道路不同方向的车道分别用不同的折线表示。本文使用的路网数据精度较高，忽略其误差。

从规划路径中获取的路网数据集合为

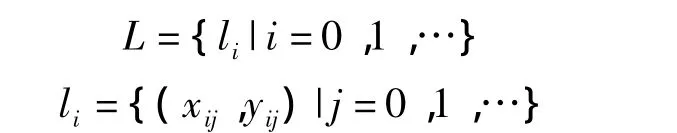
式中:li为规划路径L中的路段;(xij，yij)为路段li上的节点坐标。

2.1 路网数据的插值

由于原始路网数据稀疏且分布不均，直接根据地图路网数据进行曲线拟合很难取得良好效果。针对这一问题，首先对路网数据进行插值处理，在不改变道路几何形状的前提下，增加原始点数量，生成足够多的拟合点，提高曲线拟合精度。

电子地图的路径规划生成的是一条以起点和终点为端点、经过有限个节点的连续折线，用S表示起点到折线上任意一点的折线距离，S的取值与折线上的点存在一一对应的关系，因此，将S作为路网数据插值变量，并用S的大小表示路径折线中任意一点的位置，即

对折射距离变量S的插值等价于对原始路网数据的插值。

通过分析地图路网模型及各种插值方法的特点，分别采用线性插值、3次插值、样条插值处理路网数据，并将插值结果与地图规划路线进行对比(如图1所示)。

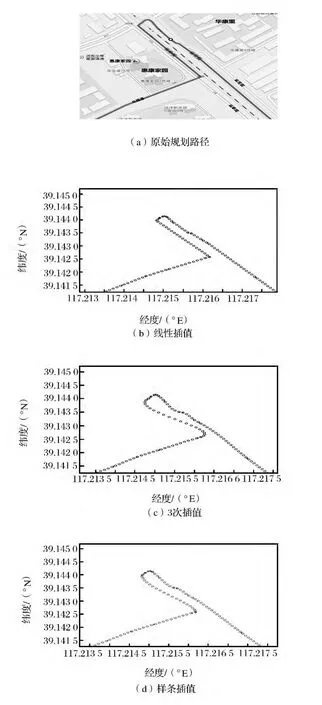
图1 3种插值方法的结果与原始规划路径对比

由于线性插值的特点与路网模型的结构类似，插值得到的数据基本保持了原始路段的几何形状;而3次插值和样条插值的结果与原始路段偏差较大。因此，采用线性插值的方式对变量S进行处理，插值间距为ρ，得到一组拟合控制点:|i=1，2，…，ma}={|i=1，2，…，ma}其中

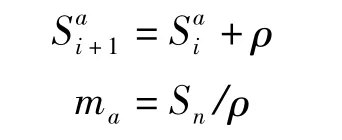
2.2 拟合导航路径曲线

路网数据的线性插值能够表达规划路径所在道路的几何形状，但车辆的实际行驶路径不可能完全与插值轨迹重合。原因是车辆行驶路径为曲率平稳变化的曲线，而线性插值得到的道路模型为连续的折线，二者在需要变更道路的路口或曲率较大的路段存在较大偏差。

由连续曲线段构成的样条曲线在道路模型的构建中有着广泛的应用。样条曲线是一个由多个分段曲线组成的线性方程组，用它进行路径几何形状的近似是非常稳定和简单的［4］。其中插值样条和逼近样条是最常用的两种。插值样条生成的路径严格穿过所有的曲线控制点，可以用控制点对路径形状进行直观的估计。其优点是可以直接使用控制点对引导路径模型进行表示，但单个控制点的改变会对曲线的形状产生较大影响。逼近样条中，曲线的控制点不一定全部落在生成的曲线上，B样条就是一种典型的逼近样条方法［5］。虽然B样条不如插值样条表示得更加直观，但其曲线的整体形状受单个控制点变化的影响较小，更加适用于智能车导航路线的生成。此外，B样条的很多性质可以用来对车辆真实的行驶路径进行近似，如凸包性、几何不变性、数值稳定性等，通过B样条拟合的曲线能够保证车辆行驶的平顺性。B样条曲线的数学表达式为

式中:p为样条的阶数;bj(j=0，1，…，n)=，为控制点;t=S，为样条参数。

控制点决定了样条的凸包性。因此，样条曲线开始于第一个控制点b0，终止于最后一个控制点bn，其间具有凸包性。节点向量T表示为

向量T中的元素为单调不减数列。为了将样条曲线的端点固定在控制点的起点和终点即b0和bn，将第一个和最后一个节点以一个定值重复p次，如下所示:

式中 j=1，2，…，p。

3 导航路径的优化

3.1 导航路径的约束模型

为使智能车在无外界环境干扰时能够准确地沿引导路径行驶，导航路径需要满足由车辆几何特性与道路几何特性决定的约束条件。

(1)车辆几何约束。转弯处的导航路径的曲率半径大于车辆自身的最小转弯半径。

(2)道路几何约束。导航路径落在规划路径所在道路的可行驶区域内。

根据这两个约束条件，构建图2所示的车辆导航路径约束模型。

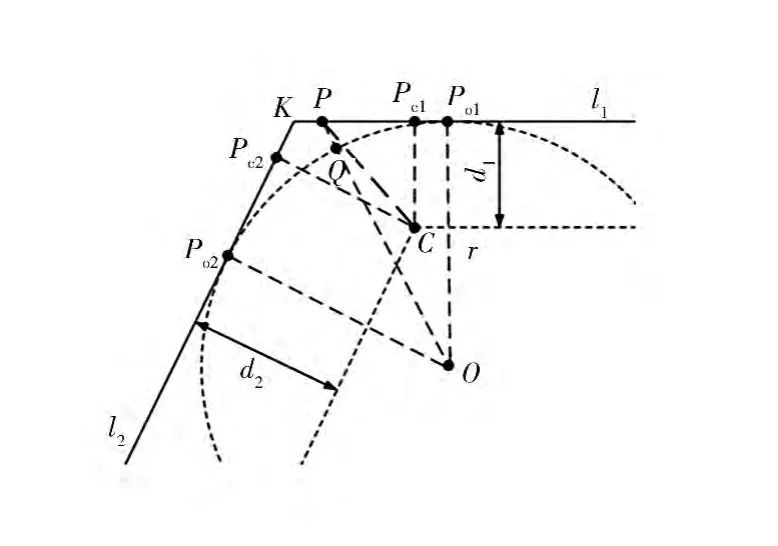
图2 车辆导航路径约束模型

图2中，P点为原始路径规划折线上的一点，P点的位置用从起点到该点的折线距离S表示。线段l1和l2表示规划路径中相邻两路段的中心线，将l1和l2沿各自法线方向向两侧平移，平移距离分别为d1和d2，得到位于中心线内侧和外侧的两组新的线段，其中内侧一组的两条线段相交于一点C。过C作l1和l2的法线，与l1和l2分别相交于点Pc1和Pc2，它们的位置可根据路段宽度及路段间夹角求得。当P点落在Pc1和Pc2之间的路段时，取|PC|－dv/2作为引导路径允许的最大偏移量 Emax(s)，即

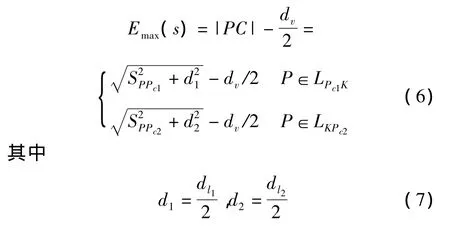
式中:dv为车身宽度;dl1、dl2为 l1、l2所在路段的路宽;SPPc1、SPPc2由 S唯一确定。

当P点落在l1的其他位置时，Emax(s)=d1－dv/2;当P点落在l2的其他位置时，Emax(s)=d2－dv/2。圆O是以r为半径、与l1和l2同时相切的圆，切点为PO1、PO2。当P点落在PO1和PO2之间的路段时，连接PO，与圆O相交于点Q，取|PQ|作为引导路径的最小偏移量Emin(s)，即

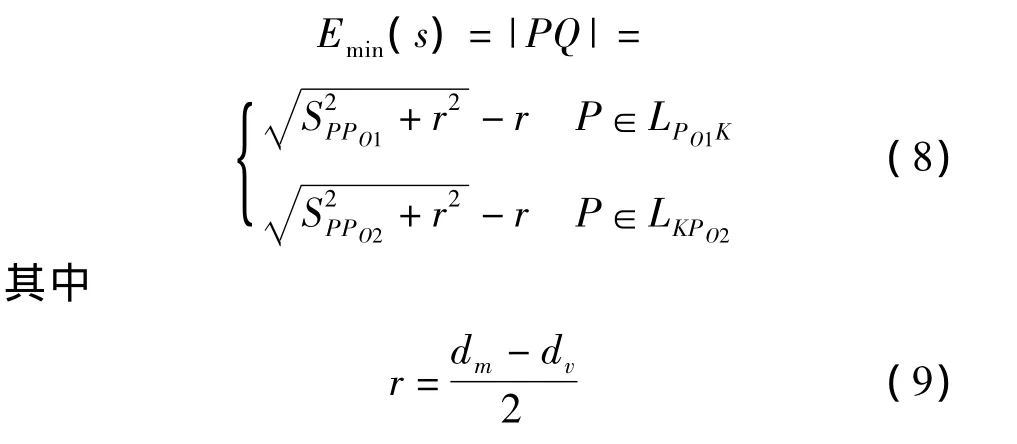
式中:dm为车辆的最小转弯直径;SPPO1、SPPO2由S唯一确定。

当P点落在l1、l2上其他位置时，Emin(s)=0。

取P点到拟合曲线的距离为eP，表示拟合曲线与原始规划路径之间的偏差。在给定路线上，对任意一点P，若eP均满足

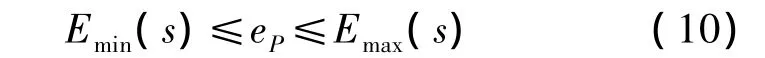
则认为导航曲线满足其约束条件。

3.2 拟合曲线的优化

在生成智能车的导航曲线后，要对其是否满足约束条件进行检验和调整。由于导航曲线是对控制点进行B样条拟合得到的，控制点的数量和位置决定了曲线拟合的质量;而控制点是由原始数据通过线性插值产生的，其数量可由线性插值的密度进行控制。因此，可通过调整控制点的插值间距ρ来改变导航曲线的生成效果，从而改变eP的大小，使其满足式(10)的关系。对于给定的路线，eP和ρ之间满足一一对应且单调的函数关系，即插值间距ρ越小，同一位置点P对应的eP越小。但由于无法求出eP和ρ之间的具体函数关系，故无法根据约束条件直接确定ρ的取值。对此，本文提出了基于迭代的自适应修正算法，引入偏差修正系数k和修正偏差m，根据m的大小实现k的自适应调整，从而对ρ值进行修正，使eP快速收敛到约束条件范围内。算法流程如下:

(1)已知eP的约束条件为［Emin(s)，Emax(s)］，给定插值间距的初值ρ0，初始调整系数k0，初始调整偏差m0，并求ρ0对应的eP。

(2)判断eP是否满足约束条件，若满足，调整结束，得到ρout;否则，计算eP与约束条件上限和下限的差值。

若存在ep＞Emax(P)，则在大于上限的点中取出差值最大的一点P0，其位置为S0，令

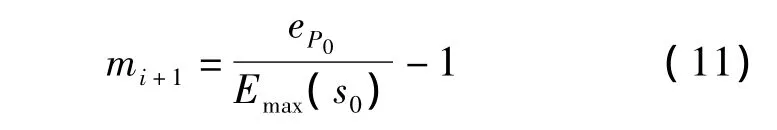
若存在eP＜Emin(P)，则在小于下限的点中取出差值最大的一点P0，其位置为S0，令

若大于上限和小于下限的点同时存在，则将曲线分段，分别对每段曲线进行修正。

(3)按照式(13)、(14)计算 ρi+1和 ki+1。

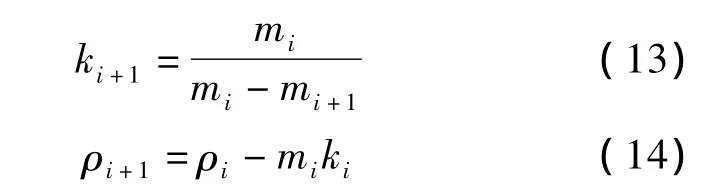
式中 i=0，1，…。

以ρi+1为插值间距更新拟合曲线，并计算相应的偏差值eP，返回步骤(2)。

通过该算法对导航路径进行修正，得到智能车导航路径的数据集合

4 实验验证

使用百度地图规划导航路径，规划结果如图3所示。实验路段起点为图上A点，终点为图上B点。路径总长5.3 km，包括了直道、弯道、路口转弯、掉头等路段。获取规划路径上的节点坐标并进行纠偏，得到该路段的路网数据。使用第2章“导航路径的生成”方法对该数据进行处理，生成了智能车导航路径。原始路网数据及智能车导航数据如图4所示。

图3 百度地图规划结果

图4 原始路网数据及智能车导航数据

选取路程 S∈［3.8，3.9］km 处的路段，取dm=11 m，dv=1.8 m，m0=1，k0=1，ρ0=8.5。将试验车的车宽dv、最小转弯直径dm以及该路段的路宽数据代入本文的约束模型，得到该路段下导航路径偏移量eP的取值范围;根据取值范围对该路段的初始导航路径进行自适应修正，得到了满足约束条件的导航路径。车辆在该路段需要进行一次掉头，由于道路较窄，导航路径的约束条件比较苛刻。图5为该路段中导航路径与中心线的偏差与位置的函数关系。其中，实线为约束条件确定导航路径偏移量的取值上限Emax(s)和取值下限Emin(s)，虚线为不同ρ值对应的导航路径的偏移量eP。图6为不同ρ值对应的智能车导航路径，在导航路径上每隔1.5 m取一个点，点的直径为试验车车宽。当控制点插值间距ρ=ρ0=8.5时，车辆沿导航路径行驶会碰到道路边沿，通过修正，得到一条较好的无碰路径，如图5(b)、图6(b)所示。

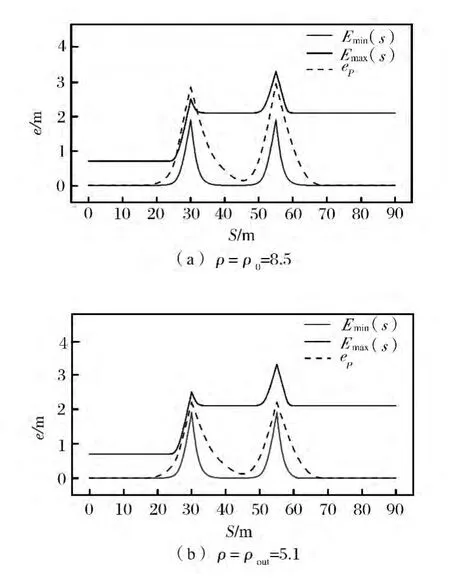
图5 不同ρ值对应的与S的关系曲线

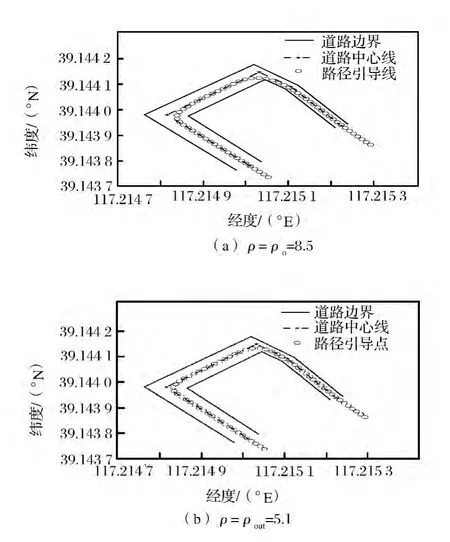
图6 不同ρ值对应的智能车导航路径

5 结语

本文提出的一种基于常规电子地图稀疏坐标的导航路径校正方法，无需事先构建驾驶地图，直接通过提取现有电子地图的路网数据，利用插值、拟合处理与本文提出的基于模型约束的导航路径自适应修正方法，实现对智能车行驶的精确导航。下一步将针对导航路径约束模型，对车辆行驶速度等运动学约束以及约束范围内的最优路径进行研究。

［1］ Handel P.Handbook of Intelligent Vehicles［M］.London:Springer，2012:344-361.

［2］ Levinson J S.Automatic Laser Calibration，Mapping，and Localization for Autonomous Vehicles［D］.Palo Alto:Stanford University，2011:25-39.

［3］ Castro M，Iglesias L.Geometric modelling of highways using global positioning system(GPS)data and spline approximation［J］.Emerging Technol，2006，14(4):233-243.

［4］ Jo Kichun，Sunwoo Myoungho.Generation of a precise roadway map for autonomous cars［J］.IEEE Transaction on Intelligent Transportation System，2014，15(3):925-937.

［5］ Chen A，Ramanandan A，Farrell J A.High-precision lane-level road map building for vehicle navigation［C］//IEEE/ION PLANS，2010:1035-1042.