脉冲星导航的相对论定位法(Ⅰ)：相对论定位系统

费保俊，黄文宏，孙维瑾，贺珍妮

(1.装甲兵工程学院 基础部，北京 100072；2.北京师范大学 物理系，北京 100875)

脉冲星导航的相对论定位法(Ⅰ)：相对论定位系统

费保俊1，黄文宏2，孙维瑾1，贺珍妮1

(1.装甲兵工程学院 基础部，北京 100072；2.北京师范大学 物理系，北京 100875)

为了讨论脉冲星导航的相对论定位法，介绍近年来国际上兴起的相对论定位系统。它是以导航星座的固有时间(即自身携带时钟记录的时间)为坐标的一种新型的定位方法，相对于以导航星座时空坐标为基准的方法，在一定前提下具有较大优越性。

相对论定位系统，零标架，光坐标

1 引言

无论是卫星导航还是现在正在研究中的X射线脉冲星导航(X-ray pulsar-based navigation，XNAV)，都是测量光波从导航星座(卫星或脉冲星)到达观测者的传播时间即光子到达时间(time of arrival，TOA)，由于光速不变性，TOA等价于导航星座到观测者的距离，可以将这种导航方法称作TOA定位法。从纯粹广义相对论的观点来看，TOA定位法中测量的系统时间(例如北斗时(BeiDou navigation satellite system time，BDT)或全球定位系统时(global positioning system time，GPST)属于坐标时间在考虑引力作用的情况下，坐标时间并不满足光速不变性，于是将引力对测量时间的影响(相对论效应)作为一种修正加进去，因此TOA定位法实际上是一种半经典理论，是经典力学与相对论的混合体。

原则上说，直接在相对论框架内建立导航理论是完全可行的，有不少学者在这方面作了深入探讨。文献[1]在深入研究卫星导航理论过程中，首先将相对论测量理论引入导航系统，提出全球定位系统(global positioning system，GPS)中的可观测量是指固有量而并非坐标量，认为应该借鉴相对论天体物理的研究方法，在4维零标架中讨论光传播问题，文献[2]随后建立了一种共轭零标架，将对应坐标称之为GPS典型坐标；文献[3-8]将这一方法系统化，提出4个发射体的固有时间构成4维时空的光坐标或发射坐标，可以为任意观测者定位导航。由此建立起来的理论体系称之为相对论定位系统(relativistic positioning system，RPS)，它是以相对论测量理论为基础的一种全新的导航方法。

为叙述方便，本章采用c=1的自然单位制，即下文中的时间理解为通常时间的c倍，量纲为长度，速度是以c为度量单位的无量纲物理量。

2 正交标架与零标架

(1)

(2)

这里采用爱因斯坦求和惯例，即表达式中上下指标相同时表示对该指标求和。式(2)中的〈,〉定义为两个4维矢量的闵氏内积，相当于3维欧氏空间的矢量点积。该标架的特点是时间和空间概念比较清楚。

(3)

(4)

(5)

如果度规张量的对角元素gaa=0，则有

(6)

式(6)中的3维欧氏空间矢量

(7)

同理，根据度规张量的逆变分量与闵氏度规的关系

(8)

以及共轭基矢量之间的关系

(9)

可以证明，gaa=0表示每一个新共轭基矢ωa在闵氏标架的共轭时间轴e0上的分量值与3维欧氏空间的分量值相同，新共轭基矢量是零矢量。

综合上面的讨论，将

gaa=0 或gaa=0

(10)

的标架称作零标架(nullframe)或共轭零标架(conjugatenullframe)，其含义为标架的基矢量或共轭基矢量是闵氏空间的零矢量。

图1 3维闵氏空间的零标架及其在2维欧氏空间的投影

举一个3维时空零标架的例子。如图1所示，设新标架基矢量(ω1,ω2,ω3)与3维正交标架基矢量的关系是

(12)

利用式(3)可得该标架下的度规

g11=g22=g33=0

所以{ω1,ω2,ω3}构成一个3维零标架。从图中可以看出，零标架的3个基矢量均位于原点的光锥上，它们在2维欧氏空间{x1,x2}上的投影分别是

(13)

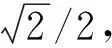
零标架的固有性质为研究光波的传播特性提供了一个非常有效的工具，下面讨论的相对论定位系统就是基于零标架的一种新的导航方法。

3 零标架中的光坐标

如图2所示，设发射体(导航星座)在闵氏空间的世界线为γa(τa)(a=1,2,3,4)，τa为发射体a的固有时。 在运动过程中发射体不断沿自身光锥发射光波，当观测者接收到4个发射体的光波时，表明发射点Pa(xa)必定位于接收点P(x)的过去光锥上，或者说接收点必定是4个发射点将来光锥的交点。由于沿光锥的时空间隔为0，即PPa的闵氏长度为0，有

0=ημν(xμ-xaμ)(xν-xaν)
=ημνxaμxaν-2ημνxaμxν+ημνxμxν
=-2+

(14)

发射点坐标(xaμ)是指发射体a的时空坐标的μ分量，当它们为已知量时，由上面4式可确定接收点的坐标(xμ)。这实际上就是卫星导航的基本原理。

图2 发射体的世界线与观测者的过去光锥

假设发射体a的3维速度va为常量，则4维闵氏速度也是常量

(15)

积分得

xaμ=xaμ(0)+uaμτa

(16)

注意式中的“0”是指τa=0，即xaμ(0)表示发射体a在τa=0时的4维初始坐标。将上式代入式(14)并利用闵氏速度内积

时空间隔变成

(τa)2-2τa+<ξa,ξa>=0

(17)

式(17)中的

(18)

是观测者相对于发射体初始位置的4维位移矢量。由此解出

(19)

这里已经舍去根号前取“+”号的另一解，因为它对应于发射体世界线与接收点的将来光锥相交，与所设条件不符。如果发射体的速度uaμ以及初始坐标xaμ(0)为已知量，上式给出发射体的固有时与观测者坐标的关系。

式(19)表明发射体的固有时是观测者坐标的函数

进一步将它当成一种坐标变换，只要变换矩阵的行列式不为0，则

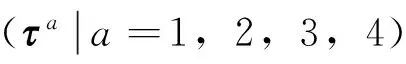
既然光坐标构成坐标系，就应该有相应的标架和度规，下面证明光坐标对应的标架正是所谓的零标架。将式(19)对坐标dxμ=dξaμ微分

(20)

式(20)中的协变分量

(21)

{τa}与{xμ}的变换系数为

(22)

由式(8)，不难求出度规张量的对角元素

(23)

因此发射坐标{τa}构成零标架。显然，式(19)也可表示成

(24)

此时可以看到，所谓相对论定位系统，其实质是以发射体(导航星座)的固有时间即4个光坐标τa而不是16个时空坐标xaμ来确定观测者的运动状态xμ，但前提是4个发射体的速度为已知常量。这4个光坐标是零标架的4个分量，任意观测者的运动状态可以唯一地由这4个坐标所确定。

4 2维平直时空的相对论定位法

通过上面的讨论可以得到应用RPS的前提条件是导航星座应该具有确定的速度。如果导航星座可以看成分段匀速直线运动，则可以对每一段的发射体初始位置和运动速度建立零标架。如果发射体具有不变的常速度则问题变得相对简单，而X射线脉冲星在质心天球参考系(barycentriccelestialreferencesystem，BCRS)中的速度(自行)在较长时间内可以看成常数。下面来讨论2维时空中脉冲星导航的相对论定位法。

在BCRS中引入2维Newman-Penrose坐标{U,V}，与2维闵氏坐标{t,x}的关系分别为

(25)

新坐标下的线元是

dτ2=dt2-dx2=dUdV

(26)

因g11=g22=0，故Newman-Penrose标架是零标架。

设脉冲星a(a=1,2)在BCRS中的速度va为常数，根据式(15)和式(25)，可知脉冲星的闵氏速度矢量在零标架下的分量也为常量

(27)

式(27)中定义的

是va对应的闵氏时空双曲角，这里只需要理解为一个代号。设脉冲星的初始坐标分别为(Ua(0),Va(0))，由上式积分得到它们的坐标是

(28)

根据发射点(Ua,Va)与接收点(U,V)的时空间隔

(U-Ua)(V-Va)=0

(29)

解出U=Ua或V=Va。如果航天器位于两颗脉冲星之间，则接收点的坐标为

(30)

式(30)也可以根据式(19)求出。将

代入式(19)，求出脉冲星a的固有时

分别取a=1,2就得到

(31)

式(31)与式(30)完全一致。

设脉冲星的初始时空坐标满足

t1(0)=-x1(0),t2(0)=x2(0)

(32)

即U1(0)=0，V2(0)=0。则式(30)或式(31)简化成

(33)

当两颗脉冲星的速度(v1,v2)已知的情况下，航天器的时空坐标(t,x)与光坐标(τ1,τ2)或(U,V)存在一一对应关系。

图3 发射点和接收点的时空坐标(a)与光坐标(b)

下面通过图3作具体说明。

图3中{t,x}和{U,V}是正交标架和零标架，γ,γ1,γ2是航天器和两颗脉冲星的世界线。由于脉冲星做匀速运动，脉冲星世界线是2维时空的斜直线，与时间轴的夹角θ=tan-1v(取c=1)反映了脉冲星在BCRS中的速度。设两颗脉冲星的初始时间和空间坐标分别满足式(36)，实际上是要求坐标原点的光坐标为(0，0)。脉冲星不断沿自身的光锥发射光波，这些波矢量构成坐标系{U,V}的坐标网格(grid)，每一条波矢量就是一条坐标线，对应于一颗脉冲星的固有时。例如，设两颗脉冲星的固有周期分别是P1,P2，它们每隔一个周期发射一个脉冲，则图中P点对应的固有时分别为τ1=5.0P1，τ2=2.0P2，即它的光坐标为(τ1,τ2)，如果用(U,V)表示则为(ew1τ1,e-w2τ2)。

5 结束语

从本质上看，相对论定位法不是直接测量航天器的时空坐标，而是测量导航星座的固有时间，如果导航星座发射稳定的光波，就可以根据光波的相位(取决于发射体的固有时间)得到光坐标，达到导航定位的目的。

[1]ROVELLIC.GPSObservablesinGeneralRelativity[J/OL].(2001-10-12)[2014-04-21].http：//arxiv.org/pdf/gr-qc/0110003.pdf.

[2]BLAGOJEVICM，GARECKIJ，HEHLFW，etal.RealNullCoframesinGeneralRelativityandGPStypeCoordinates[J/OL].(2001-11-27)[2014-04-21].https：//archive.org/stream/arxiv-gr-qc0110078/gr-qc0110078_djvu.txt.

[3] COLL B，FERRANDO J，MORALES J.Two-dimensional Approach to Relativistic Positioning Systems[J/OL].(2006-05-22)[2014-04-21].http：//arxiv.org/pdf/gr-qc/0602015.pdf.

[4] COLL B，FERRANDO J，MORALES J.Positioning with Stationary Emitters in a Two Dimensional Spacetime[J/OL](2006-11-02)[2014-04-21].http：//syrte.obspm.fr/～coll/Papers/CoordinateSystems/StatEmitters2L.pdf.

[5] COLL B，POZO J.Relativistic Positioning Systems：the Emission Coordinates[J/OL].[2014-04-21].https：//archive.org/stream/arxiv-gr-qc0606044/gr-qc0606044_djvu.txt.

[6] RUGGIERO M L，TARTAGLIA A.Mapping Cartesian Coordinates into Emission Coordinates：Some Toy Models[J/OL].[2014-04-21].http：//arxiv.org/pdf/0710.0788v1.pdf.

[7] BINI D，GERALICO A，RUGGIERO M L，et al.Emission Versus Fermi Coordinates：Applications to Relativistic Positioning Systems[J/OL].[2014-04-21].https：//archive.org/stream/arxiv-0809.0998/0809.0998_djvu.txt.

[8] BUNANDAR D，CAVENY S A，MATZNER R A.Measuring Emission Coordinates in a Pulsar-based Relativistic Positioning System[J/OL].(2011-12-08)[2014-04-21].http：//arxiv.org/pdf/1107.1688v4.pdf.

Relativistic Positioning Method of Pulsar-based Navigation I：Relativistic Positioning System

FEI Bao-jun1，HUANG Wen-hong2，SUN Wei-jin1，HE Zhen-ni1

(1.Department of Fundamental Courses，Academy of Armored Force Engineering，Beijing 100072，China；2.Department of Physics，Beijing Normal University，Beijing 100875，China)

In order to discuss relativistic positioning method of pulsar-based navigation，we are going to introduce the international rise in recent years of relativistic positioning system.It is a new positioning method based on the proper time of navigation constellations(i.e.，the time recorded by its own clock).Compared with the method based on time and space coordinates of navigation constellation，it has a large advantage under certain premise.

relativistic positioning system(RPS)，null frame，light coordinates

2014-07-03

费保俊(1956)，男，湖北洪湖人，教授，主要从事应用相对论和脉冲星导航研究工作。

P131，V44

A

2095-4999(2015)-01-0019-05