地球定向参数对天文定位定向的影响分析
连月勇,张 超,谢宗特
(1.信息工程大学 导航与空天目标工程学院,郑州 450001;2.75711部队,广州 510000)
地球定向参数对天文定位定向的影响分析
连月勇1,张 超1,谢宗特2
(1.信息工程大学 导航与空天目标工程学院,郑州 450001;2.75711部队,广州 510000)
在天文定位定向中需要用到地球定向参数的预报值,实现地心地固坐标系和地心惯性坐标系之间的相互转换,但在实时解算时,无法获得最新的地球定向参数值,研究地球定向参数预报误差将有助于提高天文解算精度。介绍了天文定位定向原理,对地球定向参数在其中的应用进行了研究,并分别分析了地球定向参数短期和长期预报值的精度,以及参数预报误差对天文定位定向的影响。结果表明,一等天文测量中纬度和方位角的解算可采用365d地球定向参数预报值,经度的解算需要进行每季度预报数据的更新。以上结论在天文导航和天文测量中有较好的借鉴意义。
地球定向参数;天文定位;天文定向;极移;预报误差
1 引言
国际地球自转服务(International Earth Rotation Service,IERS)于1988年由国际大地测量学和地球物理学联合会与国际天文学联合会共同建立,综合全球各个新技术观测处理中心的结果开展地球定向参数服务。地球定向参数(Earth orientation parameters,EOP)是一组反应地球自转变化的参数,包括岁差、章动、极移、UT1-UTC和地球自转角(Earth rotation angle,ERA)等。EOP参数描述了地心地球参考系(geocentric terrestrial reference system,GTRS)和地心天球坐标系(geocentric celestial reference system,GCRS)之间的转换关系,应用于天文测量、天文导航和卫星导航等各个领域中[1]。
目前所获取的EOP参数,由于解算过程复杂,并不能提供参数的实时数据,因此进行天文定位定向时经常使用的是EOP参数的预报值。公报A文件是快速服务和预报产品,每周更新一次,数据文件包含各项地球定向参数及其计算误差,文件格式为ASCII,包含了跳秒和地球自转参数等信息,其中EOP参数的最长预报时间为1 a。
1991年至2000年,由于天体测量精度的不断提高及甚长基线干涉技术(very long baseline interferometry,VLBI)的发展等极大的提高了天体位置的观测精度,国际天文学协会(International Astronomical Union,IAU)通过了一系列关于天文参考系理论、地球自转模型和时间尺度的决议[2-4]。其中,IAU2000A岁差章动模型的预报精度可达0.2 mas,IAU2000B岁差章动模型预报精度达1 mas,在进行天文定位定向解算时可忽略岁差章动参数的误差不计,因此本文将重点针对EOP参数中的极移分量xp、yp和时间尺度关系值UT1-UTC进行具体的分析。
2 天文定位定向原理及EOP参数在其中的应用
2.1 天文定位原理
如图1所示,QWQ′是赤道,NWS为地平圈,P为北天极,Z为天顶,σ1、σ2及σ3为天球上的等高圈上的三颗恒星。由球面公式得[5-6]
cosz=sinφsinδ+cosφcosδcost
(1)
式(1)中,z为天体的天顶距,φ为测站天文纬度,δ天体的赤纬,t是测瞬天体的时角。
t=S-α+λ
(2)
式(2)中,α为天体的赤经,λ为测站的天文经度,S为观测瞬间的格林尼治真恒星时,由观测瞬间的UTC时刻T观解算得到。采用多星观测数据联立式(1)即可解得天文经纬度值。

图1 天球上球面三角形示意图
2.2 天文定向原理
天文定向方法包括时角法和高度法两种,下面仅介绍时角法天文定向的原理。如图2所示,AB是地面目标B的天文方位角,Aσ是观测时刻自然天体σ的方位角。设在格林尼治世界时Tutc观测得到自然天体的水平度盘值为Lσ, 地面目标的水平度盘值为LB, 则地面目标的方位角AB可通过式(3)解得[7-8]
AB=LB-(Lσ-Aσ)
(3)
式(3)中,天体方位角计算公式
(4)
式(4)中
t=S0+Tut1+Tut1×u+λ-α
(5)
式(5)中,α为自然天体在测瞬时刻的视赤经,δ为自然天体在测瞬时刻的视赤纬,t为天体的时角,λ和φ分别为测站的天文经度和纬度。u=0.002 737 91,S0为世界时0时对应的格林尼治恒星时。

图2 天文定向原理图
2.3 恒星视位置计算
由2.1节及2.2节可知,观测瞬间恒星的真赤道坐标α、δ是天文定位定向解算必不可少的参数,恒星视位置计算的精确度将直接影响定位定向的解算精度。恒星的星表历元平位置换算到观测历元的视位置,即视位置的计算,其计算流程如图3所示。
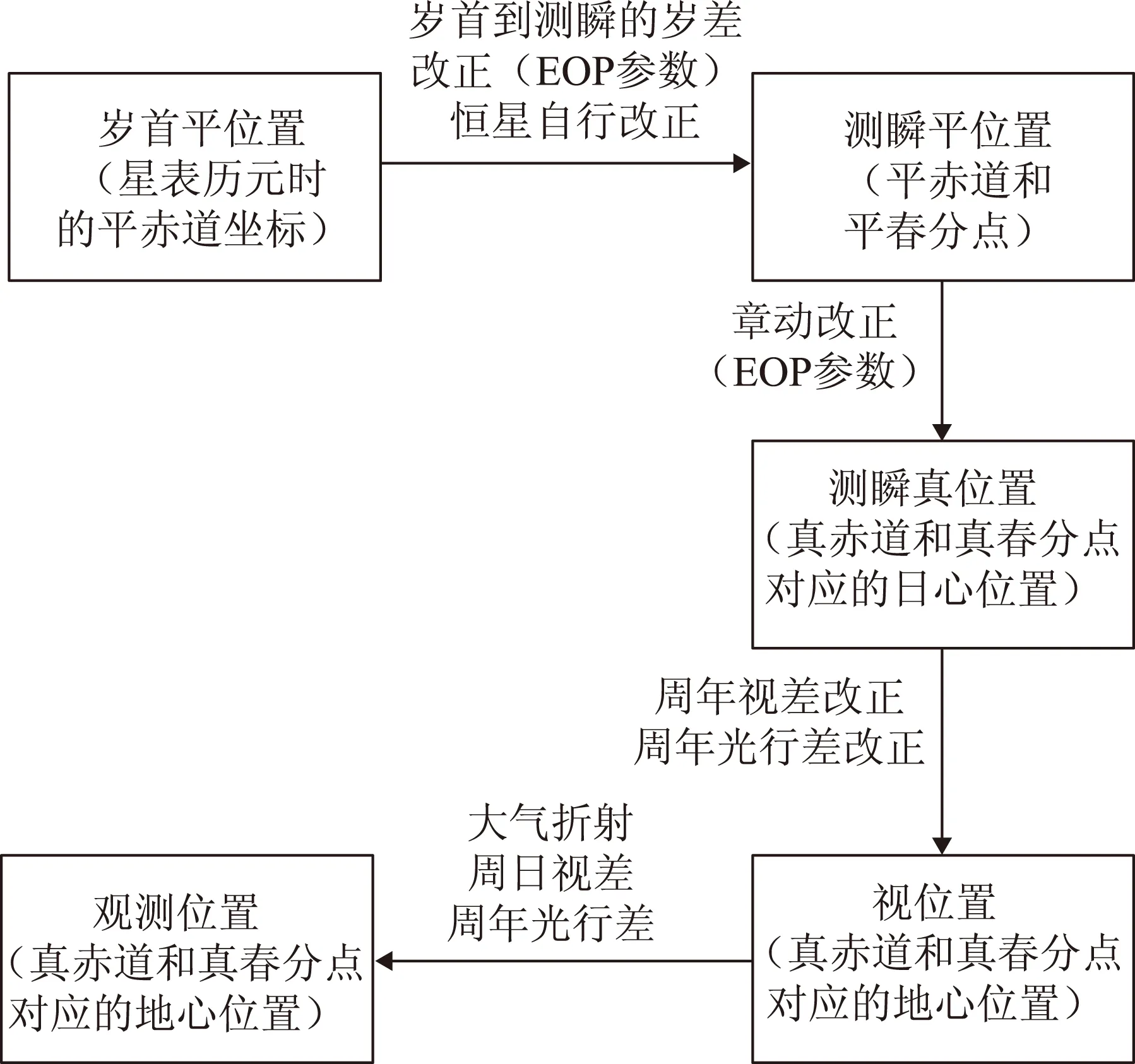
图3 恒星视位置计算流程图
此时的观测位置所解算的天文经纬度(λ、φ)和方位角(a)是相对于测瞬真北极的,由于地极移动使地面各点的子午圈发生变动,需要利用EOP的极移参数将天文成果归算到平北极(λ0、φ0、a0)。改正方法为[9]
(1)经纬度的极移改正为
(6)
(2)方位角的极移改正为
(7)
3 EOP预报误差分析
利用2010年到2013年6月这三年半期间所公布的182个公报A文件,对IERS发布的EOP参数的预报误差从短期预报和长期预报[10]两个方面进行详细分析。
3.1 短期预报误差分析
1)1 d预报误差
把IERS网站所发布的2010年到2014年的CO4文件所提供的EOP参数作为真值,将以上的182个公报A文件中的第一天预报值同对应真值进行比较,得到了182个1 d预报数值的误差,其分布如图4所示。
从图4可以看出,1 d预报误差精度较高,且稳定性好,浮动较小,并以零值为中心呈现不规则分布。极移分量xp的误差绝对值基本上在1mas以内,极移分量yp的误差绝对值大都在0.5mas以内,UT1-UTC误差绝对值都在0.2mas内。
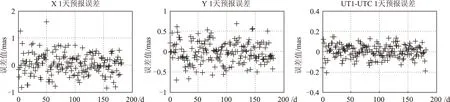
图4 1 d的EOP参数预报误差
表1给出了1d预报误差值的最大绝对值、均值和标准差,作为预报精度的参考。
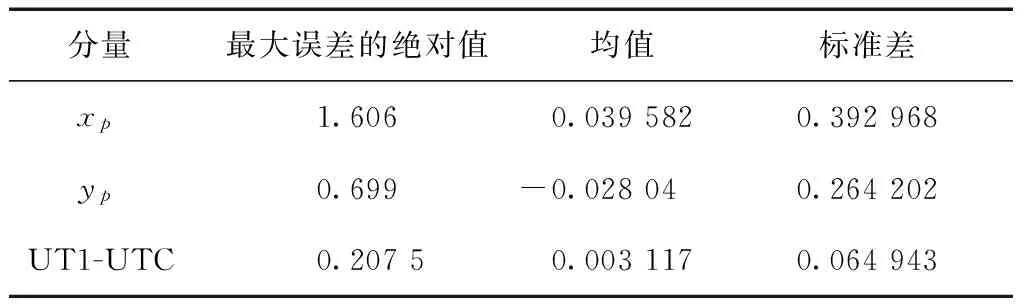
表1 1 d的EOP预报误差指标/mas
2)7 d预报误差
因为IERS网站每周进行一次公报A的更新,研究前7 d的预报值精度对天文测量和天文导航具有很好的借鉴意义[11]。将以上的182个公报A文件中的第一周预报数据同对应真值进行比较,得到参数的误差值如图5所示。
从图5可以看出,7 d预报误差随着天数增加而增大,每周的误差情况相似,误差值比较稳定,整体上呈现以零值为中心不规则分布。极移分量xp的误差绝对值在10mas以内,极移分量yp的误差绝对值都在5mas以内,UT1-UTC误差绝对值大都在1mas。
表2给出了3.5(a)内7d预报误差的最大绝对值、均值和标准差。
3.2 长期预报误差分析
选取2010年到2012年发布的公报A文件和之后发布的相应的CO4文件,两者比对求出1 a预报值和真值的差值,结果如图6所示。
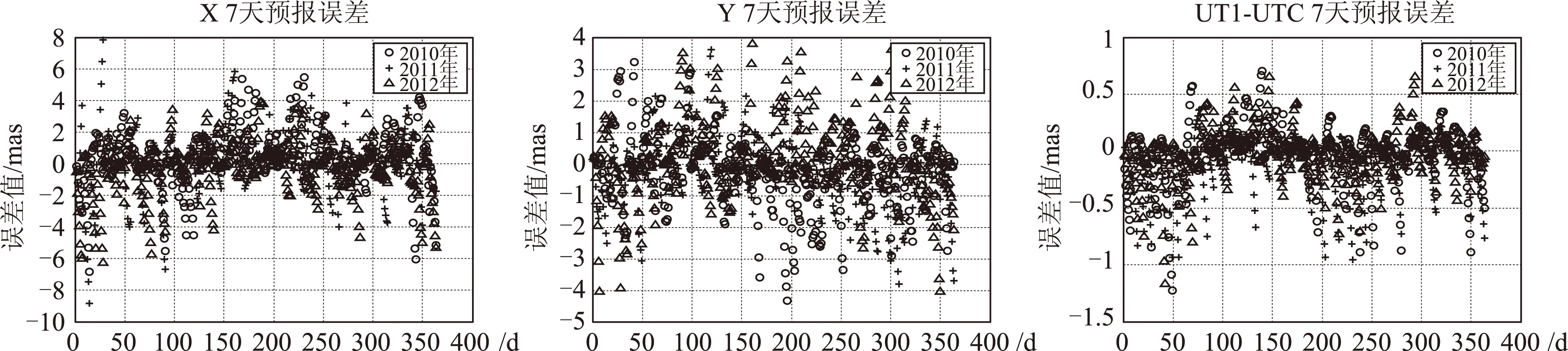
图5 7 d的EOP参数预报误差
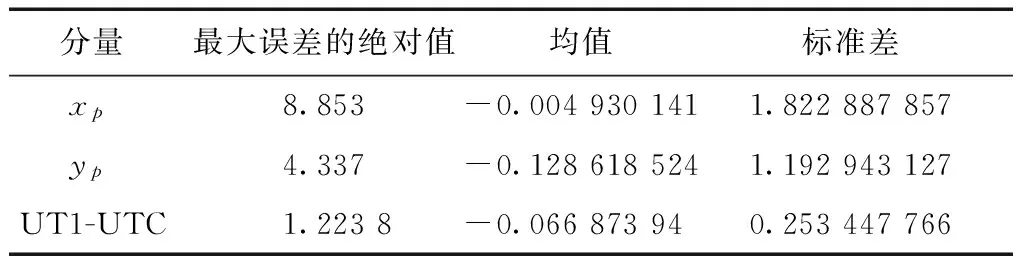
表2 7 d的EOP预报误差指标/mas
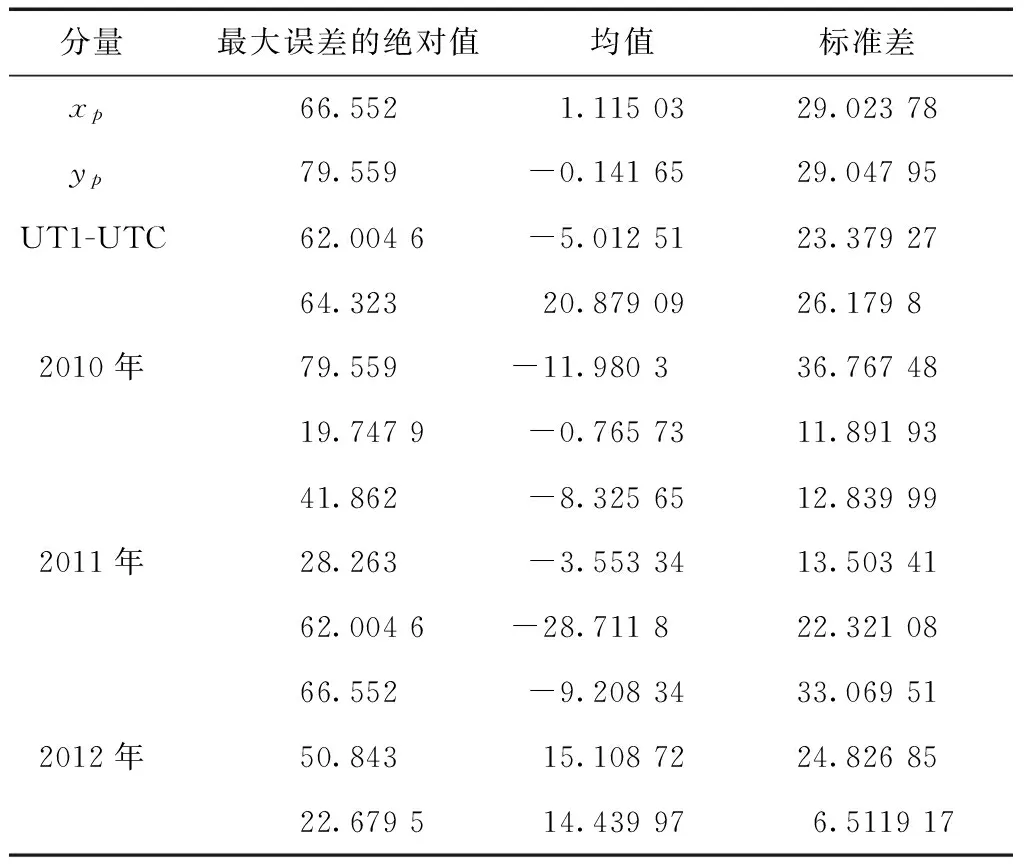
因为极移中包含周年周期和张德勒等分量,故而其预测有周期性,由图6可看出,1 a的EOP误差值存在一定的周期性。表3给出了三年总的及各个年份的EOP参数的各项指标。
由表3可知,xp全年的预报误差在67mas以内,yp全年的预报误差在80mas以内,UT1-UTC全年的预报误差在62mas以内,2011年的各个参赛预报误差最小,随着年份推移,整体预报准确性有所提高,但不稳定。

图6 长期EOP参数预报误差
表3 1 a的EOP预报误差指标/mas
分量最大误差的绝对值均值标准差xp66.5521.1150329.02378yp79.559-0.1416529.04795UT1-UTC62.0046-5.0125123.3792764.32320.8790926.17982010年79.559-11.980336.7674819.7479-0.7657311.8919341.862-8.3256512.839992011年28.263-3.5533413.5034162.0046-28.711822.3210866.552-9.2083433.069512012年50.84315.1087224.8268522.679514.439976.511917
4 EOP预报误差对天文定位定向的影响分析
根据文献[12]规定的各等天文测量要求(如表4所示),分析以上三个EOP参数不同长度预报的误差影响大小。
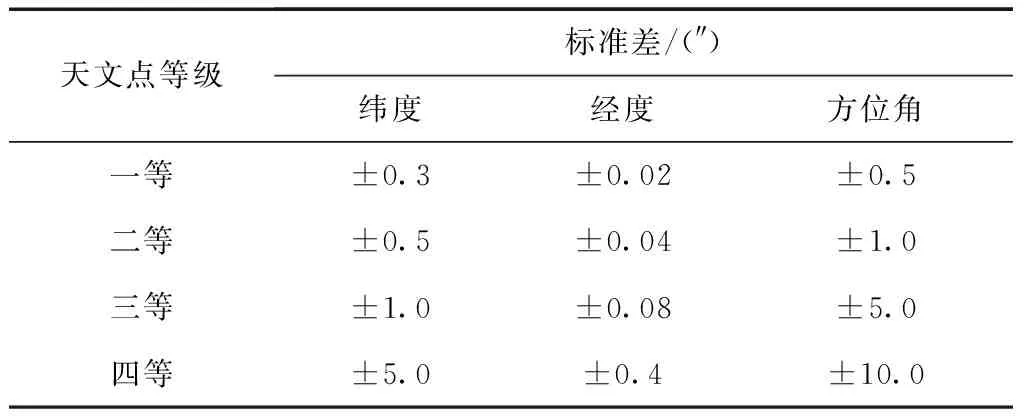
表4 天文等级测量标准
4.1 日常预报误差
EOP参数中的UT1-UTC称为日长预报,下面利用第二节中EOP预报误差的分析结果研究日长预报误差对天文定位定向的影响。
由天文定向原理可知,日长预报对于纬度的测定不产生影响。UT1-UTC主要用于恒星时角的计算,其预报误差主要体现为天文经度的误差。天文经度观测值计算如为
λ=α+n+m{+δu+δr}+δa-Sg
(8)
式(8)中,Sg是表面时刻(XE+XW)/2时的格林尼治恒星时,微分式(8)得
dλ=dSg
(9)
即日常预报误差对天文经度的影响为

(10)
微分式(4)得:
(11)
根据目前天文定向常采用观测北极星(δ≈90°)来实现,则tanδ≈+∞, 即dAN≈0, 因此日常预报误差对天文方位角基本上也不产生影响。
4.2 极移预报误差
根据式(6)及式(7)并结合短期预报误差情况,可得短期EOP预报值能够满足一等天文测量精度要求。我国地域辽阔,纬度范围3°51′N~53°33′N,经度范围73°33′E~135°05′E,由式(6)及式(7)知极移误差引起的天文解算影响关于纬度成增函数,故而取漠河(121°10′E,53°33′N)为例,分析2010年、2011年和2012年极移的365 d预报误差对天文定位定向的影响。
表5中给出了 1 a预报对天文定位定向影响的最大值、平均值和标准差,从表中可以看出,2010年和2012年的经度误差约为0.045″,超出了一等天文测量中经度±0.02″的要求。
针对1 a预报无法满足一等天文定位精度要求的情况,分别分析了1 a预报、半年预报以及一个季度预报对天文定位的影响,如表6所示。由表可知,1 a预报引起的经度误差的标准差在0.045″左右,可以满足三等天文测量经度±0.08″的要求;半年预报引起的经度误差的标准差在0.02″左右,可以满足二等天文测量经度±0.04″的要求;一个季度预报引起的经度误差的标准差不超过0.02″,可以满足一等天文测量经度±0.02″的要求。

表5 1 a预报对天文测量影响
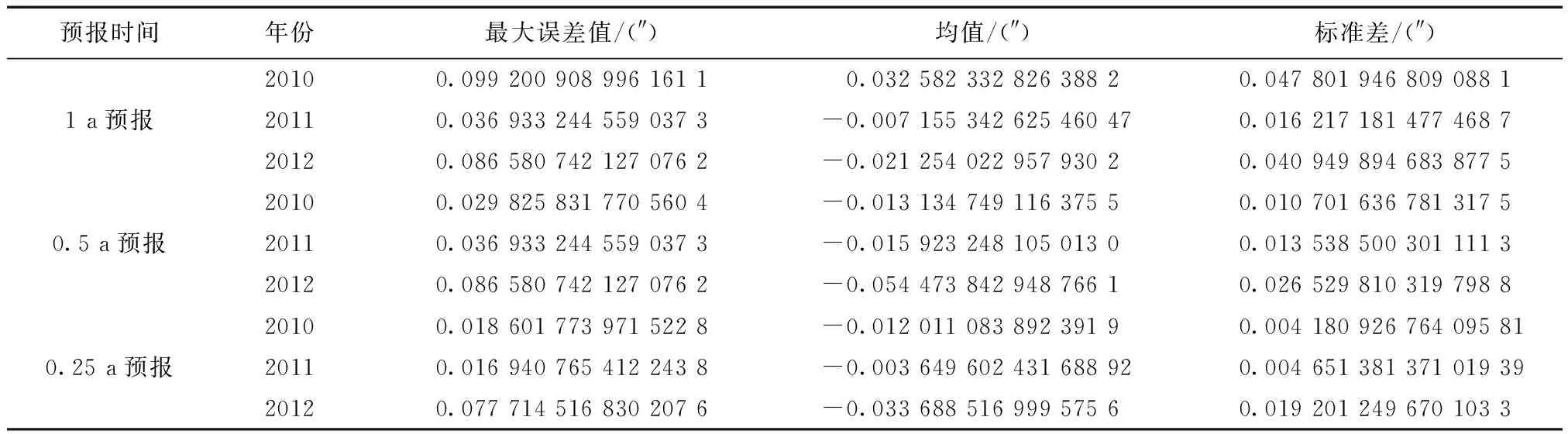
表6 经度误差分析
5 结束语
本文综合各参考文献所述关于EOP参数预报分析的方法和结论,借鉴其中提出的比较好的分析方法并结合自身所做工作,对EOP参数的预报从长期和短期两方面进行了详细深入的分析,分别得到了1 d、7 d和1 a的预报分析结果。结合平时工程运用情况,将EOP预报误差对天文定位定向的影响按照国家天文测量标准进行分门别类的分析,得到以下有益结论:
(1)1 d预报误差精度较高,且稳定性好,浮动较小,并以零值为中心呈现不规则分布。极移分量xp的误差绝对值基本上在1mas以内,极移分量yp的误差绝对值大都在0.5mas以内,UT1-UTC误差绝对值都在0.2mas内。7d预报误差随着天数增加而增大,极移分量xp的误差绝对值在10mas以内,极移分量yp的误差绝对值都在5mas以内,UT1-UTC误差绝对值大都在1mas内。
(2)1a的EOP误差值存在一定的周期性。xp全年的预报误差在67mas以内,yp全年的预报误差在80mas以内,UT1-UTC全年的预报误差在62mas以内,随着年份推移,整体预报准确性有所提高,但不稳定。
(3)日常预报(UT1-UTC)误差对天文纬度没有影响,对天文方位角基本不产生影响。1d日常预报误差对经度的最大影响约为0.207 5mas,一周日常预报误差对经度的最大影响约为1.223 8mas,1a日常预报误差对经度的最大影响约为62.046mas,都能够满足一等天文测量精度要求,可在解算时直接使用日常预报1a的预报值。
(4)极移预报误差对纬度误差不超过±0.03″,方位角误差的标准差在0.05″左右,能满足一等天文测量精度要求。1a极移预报引起的经度误差的标准差在0.045″左右,可以满足三等天文测量要求;0.5a极移预报引起的经度误差的标准差在0.02″左右,可以满足二等天文测量要求;一个季度极移预报引起的经度误差的标准差不超过0.02″,可以满足一等天文测量要求。因此,进行一等天文定向解算时可直接使用365d的极移预报值,进行一等天文定位解算需对极移预报值进行季度更新。
综合本文的分析,在进行天文定向定位时,各EOP参数预报误差所产生的影响不可忽略,进行天文解算时必须加以考虑,必要时及时进行预报数据的更新。
[1]MCCARTHYDD,PETITC.IERSConventions(2003)[M].FrankfurtamMain,Germany:VerlagdesBundesamtesfürKartographieundGeodäsie,2004.
[2] 刘佳成,朱紫.2000年以来国际天文学联合会(IAU)关于基本天文学的决议及其应用[J].天文学进展,2012,30(4):411-437.
[3] 刘佳成.新天文参考系若干问题的研究[D].南京:南京大学,2012.
[4] 夏一飞,金文敬.新参考系的引入对天体测量学的影响[J].天文学进展,2004,22(3):200-208.
[5] 张超,郑勇,夏治国.多星近似等高法同时测定天文经纬度的研究[J].测绘通报,2006(11):3-5+15.
[6] 张捍卫,许厚泽,王爱生.天文经纬度和天文方位角测定的基本原理[J].测绘科学,2006,31(4):157-160+10.
[7] 张超.基于电子经纬仪的天文测量系统及应用研究[D].郑州:解放军信息工程大学,2009.
[8] 詹银虎.基于自然天体的快速定向理论及技术研究[D].郑州:信息工程大学,2012.
[9] 王永海.CGCS2000的启用对天文定位定向的影响研究[D].郑州:解放军信息工程大学,2013.
[10]张卫星,刘万科,龚晓颖.EOP预报误差对自主定轨结果影响分析[J].大地测量与地球动力学,2011,31(5):106-110.
[11]柳文明,李峥嵘,刘文祥,等.EOP预报误差对导航卫星轨道预报的影响分析[J].全球定位系统,2009(6):17-22+27.
[12]GB/T17943—2000,大地天文测量规范[S].
[13]刘彩璋,黄杰安,戴四军.新天文常数、系统对天文经纬度和方位角的影响[J].武汉测绘科技大学学报,1988,13(3):47-55.
[14]张捍卫,郑勇,马高峰.GCRS与ITRS之间的坐标转换研究[J].大地测量与地球动力学,2011,31(1):63-67.
Influence of Earth Orientation Parameter on Celestial Fix and Astronomical Orientation
LIAN Yue-yong1,ZHANG Chao1,XIE Zong-te2
(1.College of Navigation and Aerospace Engineering,Information Engineering University,Zhengzhou 450001,China;2.Troops 75711,Guangzhou 510000,China)
The prediction of earth orientation parameters (EOP) can be used in the celestial fix and astronomical orientation,it can achieve the translation of conventional terrestial system and geocentric celestial reference system,but the latest EOP parameters value can not reach real time when calculation,so study on the prediction error of EOP is helpful to improve the calculation accuracy of astronomy.Celestial fix and astronomical orientation principle was introduced in the paper,and the application of EOP parameters was studied,the accuracy of forecasted EOP parameters on short-term and long-term were analyzed respectively,studied the effects of EOP parameters error on astronomical positioning and orientation.The results show that,365_day daily forecasting value can be used in the calculation of latitude and azimuth for an astronomical measurement,but the calculation of longitude should update the prediction value each quarter.The astronomical navigation and astronomical measurement can use these conclusions for reference.
EOP;celestial fix;astronomical orientation;polar motion;prediction error
2014-05-08
国家自然科学基金(41174025;41174026;41174027)。
连月勇(1990),男,福建泉州人,硕士生,现主要从事天文大地测量和天文导航研究。
P
A
2095-4999(2015)-01-0041-06

