三自由度直升机实验平台及姿态跟踪控制器设计
杨慧萍,高贯斌,那 靖
(昆明理工大学机电工程学院,云南 昆明650500)
0 引言
直升机飞行控制系统属于典型的多输入多输出(MIMO)系统,本身具有较强的通道耦合和非线性特性,是控制工程领域较为复杂的对象[1]。但直升机本身成本较高,维修检测工程量大。介绍的三自由度直升机模型仿真模拟了直升机的动力与电子系统,可作为直升机系统的半实物仿真平台和科研教学的控制算法研究平台。
1 三自由度直升机模型系统
三自由度直升机系统包括硬件与软件,硬件部分可分为机械结构模块与电气系统模块。机械结构模块主要由基座、平衡块、俯仰轴、横侧轴、旋转轴和连接铰链组成,初始结构如图1所示。由于调试过程中金属材质较重,影响了系统控制过程中的灵活性,增加了控制的难度。因此,将横侧轴与俯仰轴换为碳纤结构,如图2所示,改善后的系统在无平衡块的情况下已能平稳起飞,系统无需添加平衡块。电气系统模块由传感器(包括加速度计、陀螺仪及编码器)、电机、滑环、运动控制器和通信电路板构成。旋转轴通过角接触球轴承与配套轴承盖安装于基座上,旋转轴与上层板之间也采用轴承连接,基座采用两层板及4根立柱的形式保证模型的稳定性。滑环可实现上下电信号的传递的同时导线不会发生缠绕[2]。俯仰轴与旋转轴之间以及俯仰轴与横侧轴之间均通过铰链连接。由加速度计、陀螺仪传感器反馈俯仰角、横侧轴角度及速度的数据,旋转轴角度与速度可通过编码器获得。系统采用闭环控制电机,使得横测轴两端的螺旋桨升力改变,从而达到控制三自由度直升机模型姿态的目的。软件部分包括嵌入式系统软件以及上位机软件。系统使用IAR对嵌入式系统编程,并编写了基于VC的上位机软件。

图1 原系统结构

图2 修改后系统结构
2 三自由度直升机系统数学建模
三自由度直升机系统的运动可拆分为俯仰、侧翻和旋转,分别由俯仰轴、横侧轴和旋转轴实现。以下是对系统的运动分析及系统俯仰轴的数学建模。
系统的动力来源是安装于横侧轴两端的电机,在电机驱动下螺旋桨的升力可描述为F1=KfU1,F2=KfU2,U1,U2分别为两电机电压,Kf为螺旋桨升力常数[3]。螺旋桨升力之和使得俯仰轴绕支点旋转,直升机系统做俯仰运动,受力结构如图3所示。
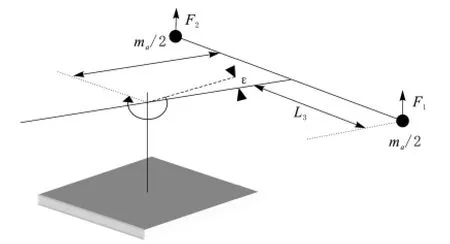
图3 三自由度直升机俯仰轴受力结构
设俯仰角为ε,直升机螺旋桨部分的质量为ma。
可得出俯仰轴的运动模型为:
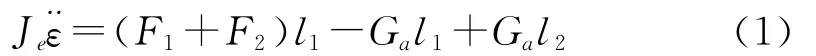
将升力表达式代入可得:

Je=+=0.14kg·m;Tg为俯仰轴产生的有效重力矩;Tg为俯仰轴产生的有效重力矩,Us=U1+U2。
3 三自由度直升机控制器设计
3.1 状态反馈跟踪控制器设计
由于系统俯仰轴、横侧轴均采用碳纤维材料,有效重力矩主要是由螺旋桨电机的等效质量产生,即第2部分中的Tg,在重力因素忽略不计的情况下,由建模分析可知,俯仰轴系统可简化为线性系统。设计状态反馈跟踪控制器实现系统对于给定的方波信号俯仰角的跟踪控制。


设计线性状态反馈跟踪控制器Vs=[k1k2]x+v,v是给定的方波信号。将Vs代入式(1)可得状态反馈闭环控制系统的表达式为:
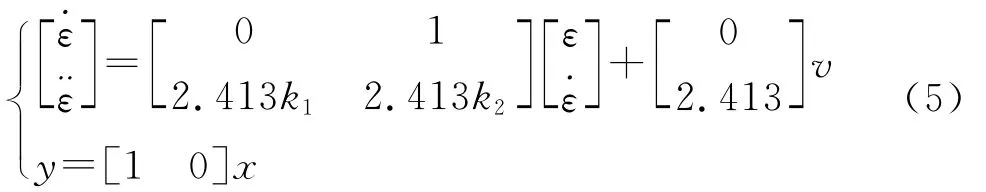
方波信号由上位机产生并通过串口发送,在方波高低电平交替变化时其瞬时差值较大,使得控制器输出控制电机时有冲击。将下位机接收到的方波作为一个二阶系统的输入,系统的响应输出作为目标跟踪曲线。二阶系统为,参数a,b的选择是根据二阶系统的特征参量确定,设置峰值时间为tp=1.57s,固有频率ωn=4.588Hz,阻尼比ε=0.9。因此可得a==21.05,b=2=8.259。基于Matlab对2种情况下三自由度直升机俯仰轴系统对方波的姿态跟踪进行了仿真,结果如图4、图5所示。

图4 状态反馈控制器方波跟踪

图5 状态反馈控制器对经过二阶系统的方波的跟踪
由图可知,方波经过二阶系统后的跟踪效果更好,超调更小。
3.2 神经网络自适应控制器
考虑三自由度直升机系统的非线性,俯仰轴的状态方程表示为:

则跟踪误差为:


设计神经网络自适应控制器



a,b均为正常数,由上可得三自由度直升机俯仰轴系统为一致最终有界[4]。
在神经网络自适应控制器的方波跟踪过程中,方波也经过了二阶系统,基于Matlab的神经网络自适应控制器对经过二阶系统后的方波的仿真跟踪结果图6所示。
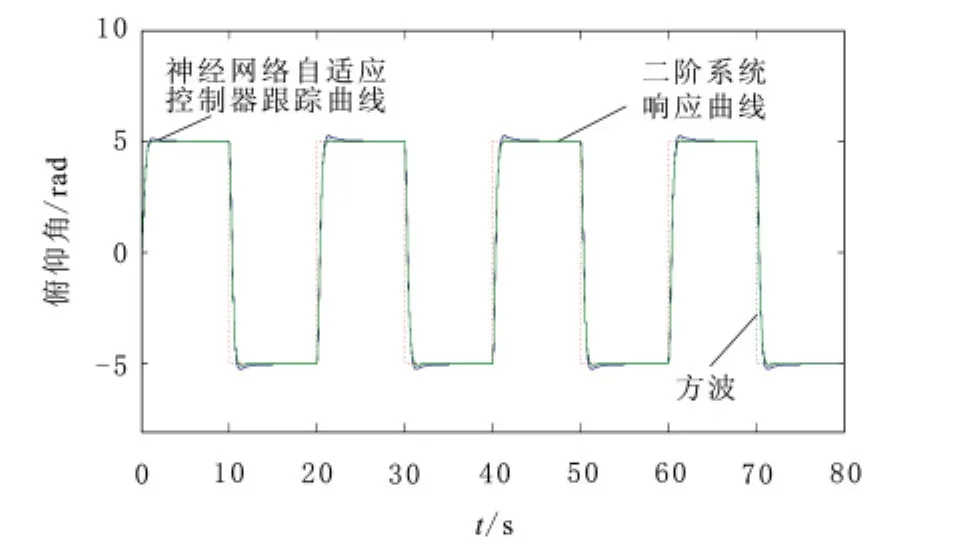
图6 神经网络自适应控制器对经过二阶系统的方波的跟踪
对比状态反馈跟踪控制器与神经网络自适应控制器仿真跟踪结果,可知后一种控制器超调降低,控制效果更好。
4 三自由度直升机上位机软件设计
采用VC设计了三自由度直升机的控制及图形显示软件。该软件可以完成以下功能:①使用按钮控制设备的启动与停止;②通过串口的方式发送方波信号、调零指令;③在线调试状态反馈控制器参数,使其达到完善的控制效果;④显示姿态的跟踪效果,分为两种形式,一种是示波器显示方式,随着时间轴的不断移动,波形图中不断显示新的数据,可在线根据需要调节X,Y轴的刻度,并对瞬时的数据以数值的方式显示,该方式适用于观察瞬时状态,直观且界面友好。另一种只观察有限时间内的跟踪图,用于观察控制算法在系统调零时的性能参数,包括快速性、超调等。
5 实验结果显示与分析
实验过程中分别用状态反馈控制器与神经网络自适应控制器对俯仰轴进行方波跟踪控制。控制系统的反馈数据包括角度与速度,分别由加速度计与陀螺仪获得,通过基于VC的上位机发送指令并记录、实时显示跟踪图形。
5.1 状态反馈控制器
控制器的反馈控制率通过在线实验调试得较优结果[1],其控制效果如图7所示。状态反馈控制器可实现方波的跟踪,但由于缺积分项,存在误差累积,出现稳态误差。
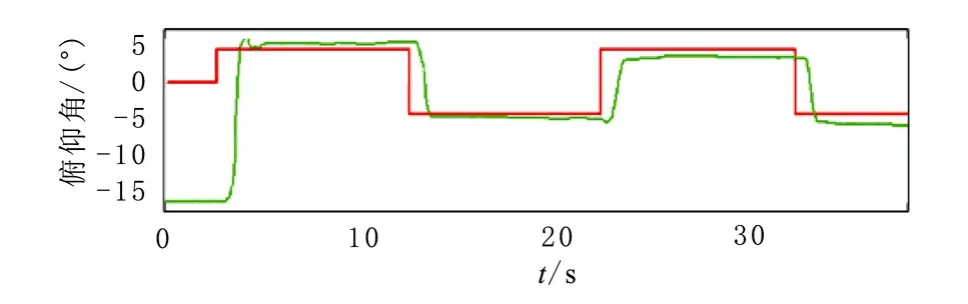
图7 状态反馈控制器的实验效果
5.2 神经网络自适应控制器
通过实验调试,神经网络自适应控制器的控制效果如图8所示。

图8 神经网络自适应控制器的实验效果
对比2个控制器的实验效果可得,神经网络自适应控制器由于自适应项使得稳态误差减小,超调减弱,效果有所改善。
6 结束语
神经网络自适应控制器的超调明显减小,控制效果较好。基于VC所编写的上位机软件实现了方波信号的产生、设备的控制、跟踪曲线的显示,通过该界面可对系统进行启停控制、状态反馈控制器参数调试、调零、方波产生的控制以及观察并分析控制效果。通过对比分析两种控制器仿真与实验结果,状态反馈控制器实现简单、稳态误差较大、不稳定;神经网络控制器减小稳态误差的同时稳定性增强。结果表明,应用后者,三自由度直升机俯仰轴系统的姿态能得到更好的控制效果。
[1] 唐光辉,侍洪波.三自由度直升机模型鲁棒控制器设计[J].华东理工大学学报(自然科学版),2011,37(1):105-111.
[2] 马云飞.三自由度直升机模拟装置的控制方法研究[D].沈阳:东北大学,2009.
[3] 王修岩,赵昌丽,李宗帅.基于系统分解的三自由度直升机控制仿真研究[J].中国民航大学学报,2009,27(6):9-12.
[4] Chowdhary G,Yucelen T,Mühlegg M,et al.Concurrent learning adaptive control of linear systems with exponentially convergent bounds[J].International Journal of Adaptive Control and Signal Processing,2013,27(4):280-301.

