高斯函数模型在变形监测数据处理中的应用

王江荣

(兰州石化职业技术学院信息处理与控制工程系，甘肃 兰州 730060)

高斯函数模型在变形监测数据处理中的应用

王江荣

(兰州石化职业技术学院信息处理与控制工程系，甘肃 兰州 730060)

建立了一种结构简单、精确度高、可操作性强的大坝变形数据高斯函数预测模型，克服了已有方法的不足。建模时利用MATLAB 遗传算法工具箱的主要函数ga()求出模型系数的初始值，再用搜索工具箱中的fminsearch 函数求出模型系数的最终值。用16期观测数据建模，再用4期变形数据对模型进行检验，检验结果表明所建模型具有很高的精确度，预测效果远好于已有的一些预测模型，为变形预测提供了一种新方法、新思路。

变形预测 高斯函数 遗传算法 MATLAB

根据变形数据对变形体的未来变化趋势能否作出准确预测，关系到能否为工程建筑设计、施工及地质灾害防治等提供科学的依据和准确的指导。建立结构简单、准确度高、稳定性好、可操作性强的变形预测模型，一直是工程技术人员的追求。目前，对变形监测数据分析和预报的方法主要有回归分析法[1]、灰色系统分析法[2]、时间序列分析法[3-4]、小波预处理的预测分析法[5-6]、卡尔曼滤波算法[7-8]、人工神经网络[9]以及频谱分析法等[10]。这些方法均取得了不错的效果，但也存在模型结构复杂、可操作性差和精确度不高等缺陷。由于变形系统是一个复杂的非线性系统，用线性回归模型不能取得理想的拟合预测效果，特别在建模时若有未考虑到的因素对变形产生影响时，这时候的预测就会产生较大的偏差。灰色系统的优点是所需数据量较少，对短期预报较为有效,但预报周期较长时，则精度较差，另外还要检验测量数据是否适合灰色系统建模。时间序列分析法必须建立在观测数据之间具有自相关性。卡尔曼滤波要求事先得知系统的初始状态，初值偏差的大小直接影响着滤波结果的精度。利用小波滤波或卡尔曼滤波对数据预处理的预测方法，往往会把一些有用信息平滑掉，致使预测结果不能完全反映实际情形；神经网络往往需要较多的训练数据才能取得理想效果，但实际训练原始数据较少，不能满足需要；频谱分析法理论强，要求时间序列的时间间隔是相等的，限制了自身的实用性，而且运算复杂，可操作性较差。基于此，笔者提出了一种基于高斯函数的多项式变形数据预测模型，用MATLAB遗传算法工具箱提供的主函数ga()和优化工具箱提供的搜索函数fminsearch()估算模型系数，即用遗传算法求出模型系数的初始值，并将所求初始值代入搜索函数fminsearch()求出模型系数的最终值。通过对建模以外的变形数据的预测分析，本研究所建模型具有很高的精确度，效果远优于支持向理机、灰色系统分析等方法，而且模型结构简单、直观，可操作性强，无需太多样本数据，值得工程技术人员借鉴。需要指出是MATLAB提供了大量的库存曲线拟合函数，可根据实际问题选取和组合，找出与实际问题匹配的曲线函数。

1 数据来源

选取某大坝上布设的1个水平变形监测点20期的水平径向位移观测值[6]，取前16期的观测值作为原始计算数据，后4期观测值与预测值进行比较，具体数值见表1。

表1 原始数据 [6]

作出前16期的原始数据散点图，如图1所示。

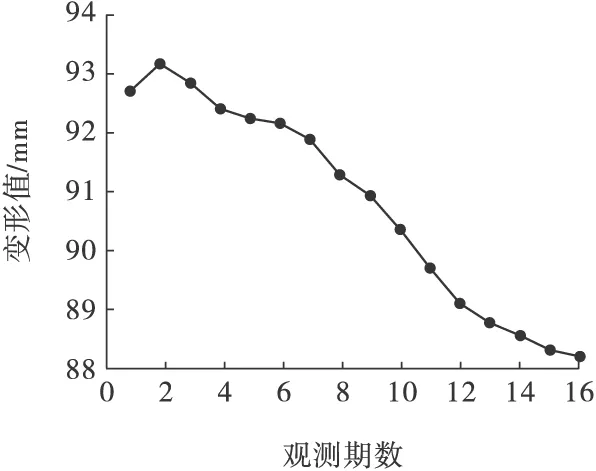
图1 原始数据散点图

根据散点图选定拟合曲线函数:从logistic曲线函数、指数函数、傅立叶级数、对数函数、高斯函数、多项式函数、幂函数、正弦和函数等中选择所需要的曲线回归模型，这些曲线函数是MATLAB的库存函数，可方便地调用。选则的依据是通过比较判定系数R2(越接近1越好)，均方根误差RMSE(越小越好)，残差平方和SSE(越小越好)等模型性能指标，选出合适的曲线模型。经过比对本研究选择高斯函数并构建如下拟合预测模型:

(1)

2 模型参数求解

2.1 遗传算法介绍

遗传算法具有全局寻优能力，且对不同数据有极强的适应能力，在解式(1)时能获得精准的参数值和目标值。应用遗传算法求解问题的算法步聚如下。

步骤1，初始化：定义种群规模M、交叉概率Pc、变异概率Pm、进化终止代数Gmax，并设置初始进化代数G=0。

步骤2，生成初始种群：随机产生N个初始结构数据，每个串结构数据成为一个个体，N个个体组成一个群体，遗传算法以该群体作为初始迭代点。

步骤3，适应度评估检测：根据实际标准计算个体的适应度，评判个体的优劣，即该个体所代表的可行解的优劣。

步骤4，遗传操作：用遗传算子生成下一代个体。采用选择算子、交叉算子和变异算子产生下一代群体。

步骤5，终止条件判断：当G>Gmax时，终止遗传算法，输出最优解；否则令

G=G+1，转入步骤3。

遗传算法的MATLAB实现，除了个性化编程(非常复杂、繁琐)外，还可以采用MATLAB提供的现成程序，即遗传算法工具箱(GeneticAlgorithmOptimizationToolbox，GAOT)。其主程序的调用格式[11]：

[x_min,fval]=ga(@fitnessfcn,nvars,

A,b,Aeq,beq,Lb,Ub,nonlcon,options)，

(2)

式中，x_min为适应度函数(目标函数)取得最小值时的参数取值；fval为目标函数在x_min的值；ga()为遗传算法工具箱中的函数；@fitnessfcn为适应度函数的句柄；nvars为适应度函数的维数，即变量数；A和b分别为不等式约束条件

Ax≤b的系数矩阵和控制向量，缺省时用[]代替；Aeq和beq分别为等式约束条件Aeqx=beq的系数矩阵和控制向量，缺省时用[]代替；Lb和Ub分别为变量的下界和上界；nonlcon为非线性约束条件MATLAB的M文件名，没有此项时可忽略；options为遗传算法的选项结构，无此项时可忽略。

MATLAB中有专用的最优化工具箱(Optimization Toolbox)，其中包含处理各种最优化问题的函数，其中用于求解多变量无约束函数最小值问题的函数有fminsearch和fminune。Fminune是基于梯度的最优化算法；而fminsearch是根据Nelder算法编写，不涉及偏导的一种优化算法。本研究选择fminsearch算法。

2.2 基于遗传算法的模型参数估算

根据式(1)定义目标函数

的元素取值为模型参数的最优估计值。利用表1 中的1～16 的观测变形数据和MATLAB编写目标函数J(θ) 的运算程序fitness(程序函数名)，程序在此略去。将待估参数θ的下限设置为Lb=-100*ones(1,9)，上限设置为Ub=100*ones(1,9)。然后在MATLAB工作窗口输入下列命令:

(3)

θ=fminsearch(@fitness，x_min).

(4)

由于遗传算法是一种随机性的搜索方法，所以每次运算可得到不同的结果。为了得到最终结果，将遗传算法式(3)得到的值作为搜索初值x_min，再用MATLAB直接搜索工具箱中的fminsearch 函数(式(4))求出最佳值θ。最终结果：

θ=[92.880 5.186 -0.379 0.888

21.540 12.060 54.740 5.799 1.816].

从而有下面的高斯模型：

(4)

模型显著性检验：均方根误差RMSE=0.120 2，残差总和SSE=0.231 1，判定系数R2=0.995 2，调整的判定系数R2=0.990 1，说明回归方程(4)是极显著的，拟合效果非常好，可用于变形值预测。

3 模型检验

在式(4)中取观测期数k=17,18,19,20，通过模型计算出后4期大坝沉降的预测值，见表2。作为对比，利用相同的建模数据建立传统灰色G(1,1)模型和支持向量机对后4期变形值预测，将预测值及文献[6]的预测值列入表2。

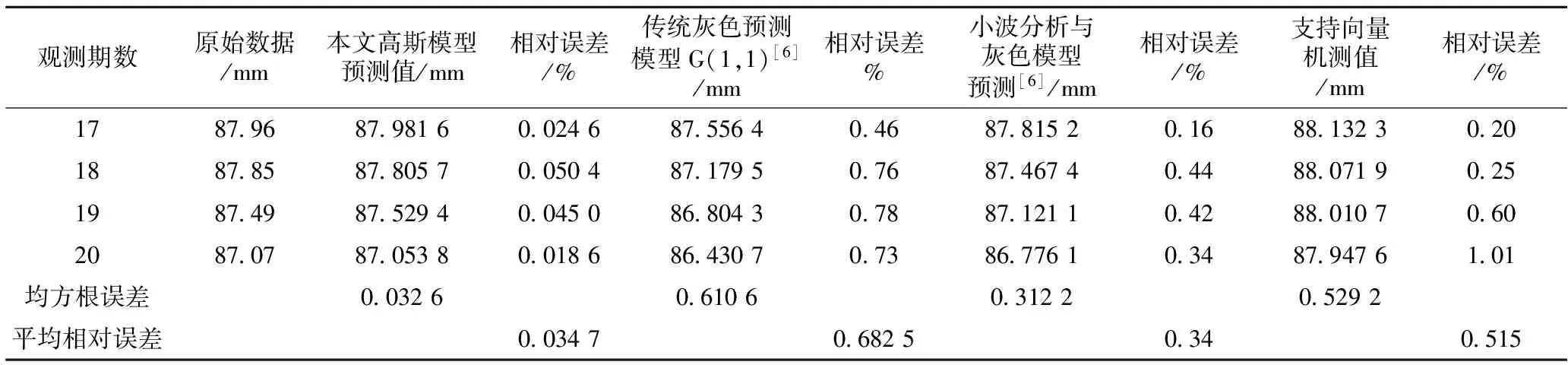
表2 高斯函数预测结果与另三个模型的预测结果

从表2给出的4种模型的预测结果和评价指标(均方根误差与平均相对误差)来看，本文模型取得了非常理想的预测效果，预测精度远好于其他3种模型。下面给出本文模型拟合预测曲线图，见图2。拟合预测曲线图显示原始观测值与高斯函数曲线非常吻合。所以本文模型的预测结果具用很高的可信度。

图2 高斯函数模型拟合预测曲线图

根据表2数据绘制出本文模型、传统灰色模型、小波分析与灰色G(1,1)相结合的预测值与实测值的点线图。分别见图3、图4和图5。很明显本研究模型预测结果远好于另外2种模型的预测结果。

图3 高斯函数预测值与实测值比较

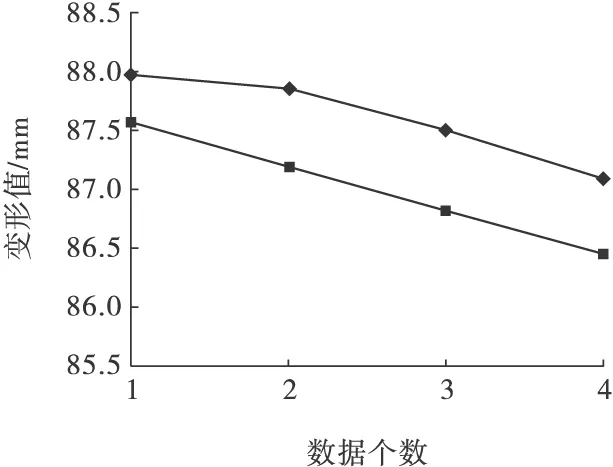
图4 传统灰色模型预测值与实测值比较

图5 小波分析与灰色模型相结合的预测值与实测值比较

4 结 语

建立高效、实用、操作性强、精确度高的变形数据预测模型是工程技术人员一直的追求，也是该领域研究的热点之一。目前已有很多变形数据预测分析方法，但大多数方法存在着理论背景深、建模过程复杂、计算量大、精确度不高等问题。本研究在已有方法的基础上，提出了一种简单、精确度高、操作方便的高斯函数初等预测模型，通过实例分析，该模型预测效果远好于已有的一些预测方法。另外、只需借助MATLAB曲线拟合工具箱提供的拟合函数和优化工具箱提供的遗传算法可方便地建立模型，其精度完全满足工程需要。对于其他类似问题只需调整拟合函数便可。所以对变形数据预测问题，本研究给出了解决这类问题的新思路、新方法，可供工程技术人员借鉴。

[1] 邹 利.回归分析在大坝变形监测数据处理中的应用研究[J].工程地球物理学报，2007，4(6):644-647. Zou Li.Application and research on regression analysis in data-processing of deformation monitoring in dam[J].Chinese Journal of Engineering Geophysics,2007，4(6):644-647.

[2] 李晓蕾.基于灰色系统理论的变形分析与预报模型应用研究[D].西安：长安大学,2008. Li Xiaolei.Study of the Application of Deformation Analyze and Prediction Model Based on Grey System[D].Xi′an：Chang′an University，2008.

[3] 冯钟萱.基于时间序列分析组合模型的变形监测分析与预报[D].西安：长安大学，2013. Feng Zhongxuan.Deformation Monitoring Analysis and Forecasting Based on Time Series Analysis Combined Model[D].Xi′an：Chang′an University，2013.

[4] 杜 琨.变形监测数据处理的方法研究[D].长沙：中南大学，2013. Du Kun.Research on Data Processing Method of Deformation Monitoring[D].Changsha：Central South University，2013.

[5] 杨 丽.小波理论在大坝变形监测数据分析中的应用研究[D].西安：西安理工大学，2010. Yang Li.Applied Research of Wavelet Theory in Dam Deformation Monitoring Data Analysis[D].Xi′an：Xi′an University of Technology，2010.

[6] 徐秀杰，黄张裕，凌晨阳，等.基于小波分析的灰色组合模型在变形监测数据处理中的应用[J].工程勘察,2014(4):80-83. Xu Xiujie，Huang Zhangyu，Ling Chenyang，et al.Application of grey theory and wavelet in deformation monitoring data processing[J].Engineering Survey，2014(4)：80-83.

[7] 王 利,李亚红,刘万林.卡尔曼滤波在大坝动态变形监测数据处理中的应用[J].西安科技大学学报,2006,26(3):353-357. Wang Li，Li Yahong，Liu Wanlin.Application of Kalman filtering in data processing of dam dynamic deformation monitoring[J].Journal of Xi′an University of Science and Technology，2006,26(3)：353-357.

[8] 张显云,张 勤,王 利.基于卡尔曼滤波的AR模型及应用[J].测绘通报,2009(11):41-43. Zhang Xianyun，Zhang Qin，Wang Li.The Kalman filtering based on AR model and its application[J].Bulletin of Surveying and Mapping,2009(11)：41-43.

[9] 严 容.基于小波去噪的 BP 神经网络在变形预测中的应用[D].北京：中国地质大学，2014. Yan Rong.The Application of BP Neural Networks in Deformation Prediction Based on Wavelet Denoising Theory[D].Beijing：China University of Geosciences，2014.

[10] 杨国华，黄 腾，韩 易.结合频谱分析的时间序列分析在变形数据处理上的应用[J].水利与建筑工程学报,2013,11(6):186-189. Yang Guohua，Huang Teng，Han Yi.Application of time series analysis combined with spectral analysis in deformation data processing[J].Journal of Water Resources and Architectural Engineering，2013,11(6)：186-189.

[11] 许国根，贾 瑛.模式识别与智能计算的MATLAB 实现[M].北京：北京航空航天大学出版社， 2012：182-183. Xu Guogen，Jia Ying.Pattern Recognition and Intelligent Computing MATLAB Implementation[M].Beijing：Beihang University Press，2012：182-183.

(责任编辑 石海林)

Application of the Gauss Function Model in Data Processing of Deformation Monitoring

Wang Jiangrong

(DepartmentofInformationProcessingandControlEngineering,LanzhouPetrochemicalCollegeofVocationalTechnology，Lanzhou730060，China)

With characteristics of simple structure，high precision，and high operability，a gauss function model of predicting deformation data for dams is set up to overcome the shortcomings of the existing methods.The main function of ga() in the genetic algorithm toolbox(MATLAB) is adopted to calculate the initial value of model coefficient，and then the fminsearch function in search toolbox is used to obtain the final value of model coefficient.16 sets of observation data are used to make modeling，and 4 groups of deformation data are used to test the model.The testing results show that the model has high accuracy，and its prediction is far better than other existing prediction model.This new model provides a new method and new idea for deformation prediction.

Deformation prediction，Gaussian function，Genetic algorithm，MATLAB

2015-02-06

甘肃省科技厅项目(编号：1204GKCA004)，甘肃省财政厅专项资金项目(编号：甘财教[2013]116号)。

王江荣(1966—),男，教授，硕士。

TD325，TD17

A

1001-1250(2015)-04-178-04