一种改进的LDPC码低复杂度最小和算法

吴 军，廖 鑫，张小红

(江西理工大学 信息工程学院，江西 赣州 341000)

一种改进的LDPC码低复杂度最小和算法

吴 军，廖 鑫，张小红

(江西理工大学 信息工程学院，江西 赣州 341000)

研究了低密度奇偶校验(Low-Density Parity-Check，LDPC)码的单最小值最小和(Single-Minimum Min-Sum，SMMS)算法，为了提高译码性能，在此基础上提出一种信道自适应可配置LDPC码最小和译码(Adaptive Configurable Min-Sum，ACMS)算法。ACMS算法在BP译码时的横向消息迭代更新过程中，LLR次小值用一个基于迭代次数的估算参数与最小值相加来取代，同时根据每次判决时的错误比特个数对不同信噪比下的估算参数进行动态修正。仿真结果表明，ACMS算法整体上提高了译码性能而仅增加少量复杂度。

低密度奇偶校验码；最小和算法；单最小值；估算参数；信道自适应

低密度奇偶校验(Low-Density Parity Check，LDPC)码是当今性能最优越的两大信道纠错码之一，Gallager对LDPC码的研究最早可以追溯到1962年[1]，MacKay和Neal于1996年重新发明它之后，LDPC码便成为了Turbo码的强大竞争对手，被广泛运用到卫星广播、深空通信、光纤网络等多个领域中，在IEEE802多个规范中和多个国家的卫星广播标准中也得到正式采用。

人工智能领域内著名的BP(Belief Propagation)算法是公认的LDPC码的最佳译码方法。近年来，在改善LDPC码BP译码性能上取得了很多有价值的研究成果，如Casado等提出的消息传递动态调度策略[2]、Wu等提出的自适应迭代译码[3]等。这些改进算法通过适当配置都可以获得非常好的译码性能，但这类算法通常消息更新策略较复杂，给硬件设计带来一定困难，不适合对译码速率有较高要求的场合。为了降低BP译码复杂度使之实用化，Fossorier提出了最小和(Min-Sum, MS)算法[4]，大幅减少了BP译码每次迭代所需的计算量。文献[5]对BP译码的接收信号进行整数量化，提高了译码速率。为了进一步减少计算复杂度，Darabiha等首次提出了基于单个最小值的最小和(Single-Minimum Min-Sum, SMMS)算法[6]。在MS算法的横向迭代消息更新中，译码器需要搜索每个比特节点传给校验节点的LLR(Log Likelihood Ratios)最小值和次小值，SMMS算法在校验节点消息更新时仅搜索第一个LLR最小值，次小值被表示为最小值加上一个固定的估算参数。

本文提出一种基于迭代次数的信道自适应可配置最小和(Adaptive Configurable Min-Sum, ACMS)算法。算法在不同信噪比下自适应修正估算参数的取值。仿真结果显示，ACMS算法整体上取得了较好的译码性能，同时其复杂度相对MS算法大幅降低，不需要对信道条件进行估计，具有一定应用价值。

1 最小和算法

1.1 传统MS算法

设一个信道采用BPSK调制，伴随均值为0、方差为σ2加性高斯白噪声ni的通信系统，若将待发送的码长为N的编码序列表示为X=(x1,x2,…,xN)T，接收端收到的信号表示为Y=(y1,y2,…,yN)T，则编码序列经过AWGN信道后的过程可以用Yi=2·xi-1+ni来表示，其中i=1,2,…,N。BP算法本质上是比特节点和校验节点的概率信息在Tanner图上交互传播的过程。为了简便起见，迭代过程中传播的软消息通常使用的是LLR值，它的绝对值表示该比特节点的可靠性大小，对二进制的LDPC码，其符号被映射为对应比特的二进制数码。LDPC码的MS算法每次都选择可靠度最低的比特节点信息对校验节点进行更新，其主要包括纵向消息传递和横向消息传递两大步骤，如式(1)和式(2)所示。

纵向更新公式为

(1)

横向更新公式为

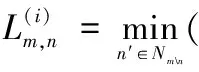
(2)

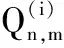
每当消息经过第i次完整的传递后，译码器便进行软判决为

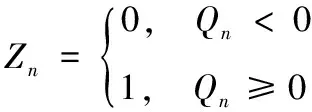
(3)

当软判决输出的码字全部满足奇偶校验方程或者达到预设的最大迭代次数时，译码器停止迭代译码并输出码字Zn。

1.2 SMMS算法

MS算法在横向更新中实际用到了一个最小值和一个次小值，次小值用于更新和同一个校验节点相邻的可靠度最低的比特节点信息，最小值则更新除此比特节点外，与该校验节点相邻的其他比特节点信息。SMMS算法简化了MS算法中次小值的计算方法，其更新表达式为

(4)

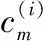
最初的SMMS算法仅对最小值进行加“1”运算得到次小值，即式中ω=1，其实现简单，但高信噪比下消息收敛过慢，存在较为严重的误码平层。其后Zhang等在改进的SMMS算法[7]中将NMS算法[8]中的偏移修正系数α引入SMMS算法，通过仿真获取最佳的ω取值，在一定程度上改善了译码性能。文献[9]提出的CMS算法为每个信噪比都配置了一个最佳估算参数，但译码器需要对信道条件进行准确估计，不利于实际应用。

2 自适应可配置最小和算法

在SMMS算法横向更新过程中，LLR次小值的大小不但取决于信噪比，而且随着迭代次数的增加发生变化。为了研究MS算法中次小值的变化趋势，本文首先使用MS算法对不同信噪比、不同迭代次数时LLR最小值和次小值的差作均值估计，定义

(5)

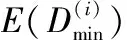
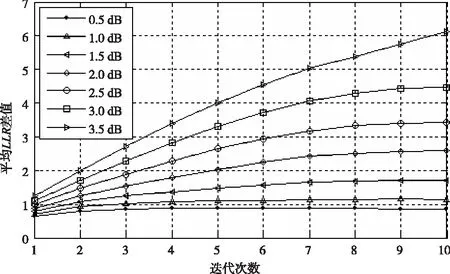
图1 MS算法中两个LLR最小值的平均差值随迭代次数的变化曲线

为了更加精确地估计LLR次小值，Fabian等提出了VWMS(Variable Weight Min-Sum)算法[10]，该算法在不同迭代次数时使用不同的估算参数对次最小值进行估计，VWMS算法改善了SMMS算法在高信噪比下的译码性能，并获得了比NMS算法还低的误码平层。VWMS算法在中低信噪比区的译码性能不如MS算法，也没有给出获取最佳估算参数的确定性方法，为不同信道条件都单独配置一组最优ω(i)值的工作量非常大，不利于算法的实现。

为了解决上述问题，本文提出信道自适应可配置最小和(Adaptive Configurable Min-Sum, ACMS)算法，ACMS算法在不同迭代区间使用不同的估算参数，同时通过每次译码的判决情况动态调整次小值所在比特节点的LLR值幅度，实现信道自适应译码。改进算法的校验节点消息更新公式为

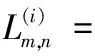
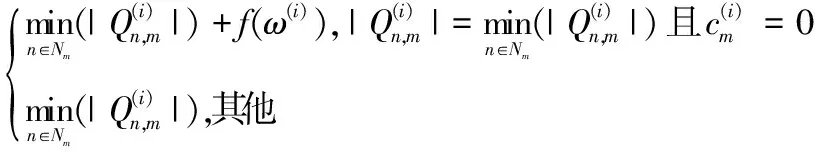
(6)

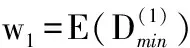
(7)

Fabian指出不宜将迭代区间划分得过多，这样会增加译码复杂度，仿真结果亦表明过多的迭代区间划分对译码性能几乎没有影响。因为在译码过程中绝大多数错误码字通常都在经过若干次迭代后就得到了纠正，在之后的迭代过程中E(Dmin)值基本稳定，故本文算法在之后的仿真分析中按照Fabian的方法将迭代区间的边界固定为I=[5 10 15 30]。将不同迭代区间配置的估算参数用式(8)表示，通过仿真来获得ω(i)的最佳配置。

wk=w1+dw·(k-1)

(8)

式中：dw为一固定常数，故wk实质上是一组等差数列。在不同信噪比时不宜将同一组ω(i)配置进ACMS算法，为了避免对ω(i)进行多次配置，ACMS算法首先在高信噪比条件下通过仿真获得最佳ω(i)后，将其乘以一个信道自适应修正因子β来修正中低信噪比条件下软消息的LLR值幅度。算法根据每次判决时错误比特的个数来判断是否使用β对次小值进行修正，判断条件为

(9)

式中：num(HT·Zn≠0)表示译码器每次判决时统计的错误比特的个数；ε为预配置的一个固定整数。

3 仿真结果及分析

为了验证改进算法的性能，分析不同参数配置对译码性能的影响，下文仿真均采用IEEE802.16e标准中码长为576、码率为0.5的准循环LDPC码，在AWGN信道下采用BPSK调制，最大迭代次数设置为30，每组信噪比下统计10 000个数据帧。

3.1 估算参数对性能的影响

为了保证高信噪比区的译码性能，本文首先配置w1=1.25，这个值是在Eb/N0=3.2 dB时按照式(5)仿真得到，然后通过改变步进间距dw的值来获得不同的ω(i)配置组，为了方便使用文献[5]中的方法对算法中接收到的信息进行整数量化，本文将dw设置为0.25的整数倍。图2是在高信噪比区，不同ω(i)配置对译码性能的影响。

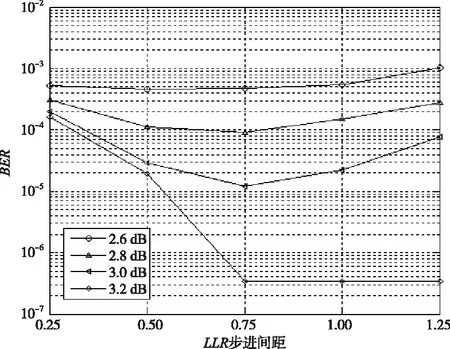
图2 ω(i)对译码性能的影响

从图中可知，当dw=0.75时，ACMS算法在高信噪区取得了最佳的误码性能。

3.2 信道自适应修正系数对性能的影响

ε取值必须适当，过高的ε在译码判决时将带来更多的运算复杂度，在中低信噪比区也不能有效抑制被高估的次小值。过低的ε值会使迭代次数增加，使算法在高信噪比区下难以收敛，给译码性能带来一定影响。图3是β值一定且Eb/N0=3 dB时，不同ε值对译码性能的影响。

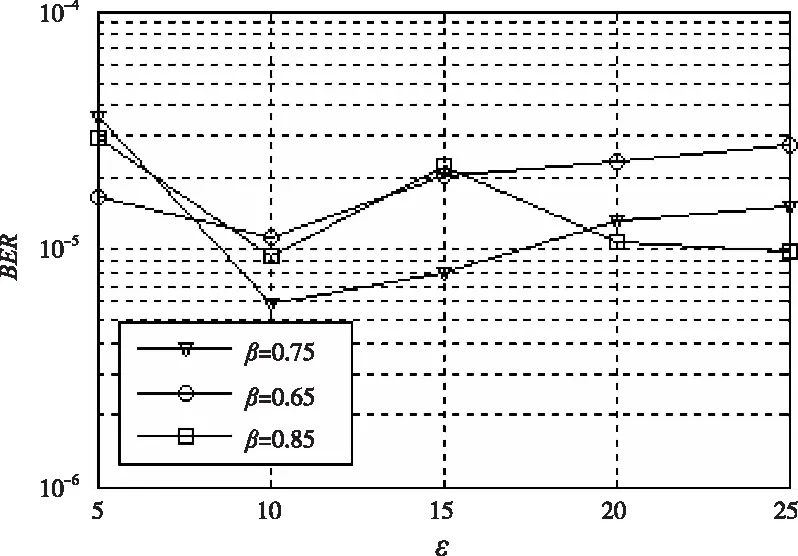
图3 ε对译码性能的影响

从图3可知，ε=10时，ACMS算法取得了最佳的性能，故本文将ε设置为10。在前文所得的最佳ω(i)和ε配置下，图4表示在不同β值对译码性能的影响。

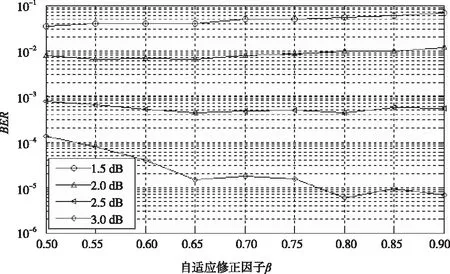
图4 自适应修正因子对译码性能的影响

从图中对比可知，在高信噪比区，当β=0.8时，ACMS算法取得了最佳的译码性能，注意到在中低信噪比区β取值越低，性能改进越明显。为了保证高信噪比下最佳的译码性能，本文将β取为0.8。

3.3 译码性能比较

各算法的参数配置归纳如表1所示，表中的偏移修正系数α为使用NMS算法仿真得出的最佳值。

表1 各算法参数配置

图5是MS、CMS、VWMS和ACMS算法的误码性能曲线。

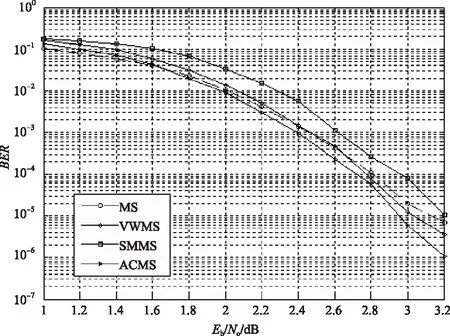
图5 各算法译码性能比较

从图中可以看出，本文提出的ACMS算法整体上优于VWMS算法。在误码率数量级为10-5时，相对VWMS算法有近0.1 dB的增益。VWMS算法在Eb/N0<2.6 dB时，其纠错性能不如MS算法，而本文提出的ACMS算法在Eb/N0>1.6 dB时，译码性能就超过了MS算法。这是因为在中低信噪比区ACMS算法抑制了VWMS算法中被高估的LLR次小值的传播。在高信噪比区，LDPC码中的陷阱集[11]的存在使部分比特收敛到一个始终不满足校验方程的错误状态。正确的比特接收到LLR值通常都很高，而错误比特的LLR值通常比较低。BP译码器接收到的LLR软判决信息随着迭代次数而增加，使得正确比特的LLR幅度和错误比特的LLR值都变得越来越大，这样译码器就始终无法纠正这些错误比特。MS算法在高信噪比下的快速收敛特性会使得比特软消息幅值更快地陷入陷阱集，而ACMS算法根据每次迭代后的判决情况，通过对LLR值的控制，适当地减缓了收敛速度，防止LLR值发生急剧变化，抑制了错误消息的传播，从而避免了比特快速收敛到一个错误的状态。

3.4 复杂度分析

对一个校验矩阵为H(M,N)且行重为r的规则LDPC码，VWMS算法在处理LLR最小值时只需进行M·(r-1)次比较运算和M次加法运算，基于两个最小值的MS算法需要M·(r-2+logr)次比较运算。虽然算法中引入的α系数增加了少量运算复杂度，但对算法进行FPGA的硬件设计时，其总体硬件开支比MS算法要少[10,12]。

在VWMS算法复杂度的基础上，本文提出的ACMS算法在硬件设计时需要增加若干存储单元用于存放β·ω(i)和ε,这些参数都可以在译码开始前配置好，在之后的校验节点和比特节点软消息迭代更新过程中没有增加任何运算量。在每次硬判决时，ACMS算法相对VWMS算法多出的计算量为统计每次判决时的错误比特个数，并做一次条件判断。由此可知，ACMS算法相比VWMS仅增加少量运算而改善了整体的译码性能，同时译码器不需对信道条件进行估计。

4 小结

针对SMMS算法对信道条件敏感的问题，本文提出了一种信道自适应的可配置LDPC码的最小和译码算法，在ACMS算法的横向迭代过程中，在不同迭代次数时采用不同的估算参数，同时引入一个信道自适应修正因子β对ω(i)的LLR值进行动态修正，这样就省去了在不同信噪比下对ω(i)的多次配置。仿真结果表明，ACMS算法整体性能优于VWMS算法, 在中高信噪比区的纠错性能也优于基于2个最小值的MS算法。由于ACMS算法省去了次小值的计算，因此更适合硬件的快速实现。

[1]GALLAGER R G. Low-density parity-check codes[J]. IRE Trans. Information Theory, 1962, 8(1): 21-28.

[2]CASADO A I V, GRIOT M, WESEL R D. LDPC decoders with informed dynamic scheduling[J]. IEEE Trans. Communications, 2010, 58(12): 3470-3479.

[3]WU X, SONG Y, JIANG M, et al. Adaptive-normalized/offset min-sum algorithm[J]. IEEE Communications Letters, 2010, 14(7): 667-669.

[4]FOSSORIER M P C, MIHALJEVIC M, IMAI H. Reduced complexity iterative decoding of low-density parity check codes based on belief propagation[J]. IEEE Trans. Communications, 1999, 47(5): 673-680.

[5]马汇淼, 马林华, 张嵩, 等. 基于整数运算的 LDPC 码改进最小和译码算法[J]. 电视技术, 2013, 37(17): 197-199.

[6]DARABIHA A, CARUSONE A C, KSCHISCHANG F R. A bit-serial approximate min-sum LDPC decoder and FPGA implementation[C]//Proc. IEEE International Symposium on Circuits and Systems. Greece: IEEE Press, 2006:1-4.

[7]ZHANG C, WANG Z, SHA J, et al. Flexible LDPC decoder design for multigigabit-per-second applications[J]. IEEE Trans. Circuits and Systems I: Regular Papers, 2010, 57(1): 116-124.

[8]CHEN J, DHOLAKIA A, ELEFTHERIOU E, et al. Reduced-complexity decoding of LDPC codes[J]. IEEE Trans. Communications, 2005, 53(8): 1288-1299.

[9]张光荣, 徐鹰, 卫国. 一种可配置的 LDPC 码最小和译码算法[J]. 中国科学技术大学学报, 2008, 38(7): 792-796.

[10]ANGARITA F, VALLS J, ALMENAR V, et al. Reduced-Complexity Min-Sum algorithm for decoding LDPC codes with low error-floor[J]. IEEE Trans. Circuits and Systems I: Regular Papers,2014(99):1-9.

[11]CHILAPPAGARI S K, NGUYEN D V, VASIC B, et al. On trapping sets and guaranteed error correction capability of LDPC codes and GLDPC codes[J]. IEEE Trans. Information Theory, 2010, 56(4): 1600-1611.

[12]WEY C L, SHIEH M D, LIN S Y. Algorithms of finding the first two minimum values and their hardware implementation[J]. IEEE Trans. Circuits and Systems I: Regular Papers, 2008, 55(11): 3430-3437.

吴 军(1963— )，副教授，主研无线通信、嵌入式系统；

廖 鑫(1990— )，硕士生，主研LDPC码译码；

张小红(1966— )，女，教授，主研信息安全、细胞神经网络、广义混沌同步。

责任编辑：薛 京

Improved Min-sum Algorithm with Low Complexity for Decoding LDPC Codes

WU Jun, LIAO Xin, ZHANG Xiaohong

(CollegeofInformationEngineering,JiangxiUniversityofScienceandTechnology,JiangxiGanzhou341000,China)

In order to reduce the performance loss of SMMS (Single-Minimum, Min-Sum) algorithm for decoding LDPC (Low-Density Parity-Check) codes, the ACMS (adaptive configurable Min-Sum) algorithm is proposed in this paper. Only the absolute minimum is used in this algorithm to update the check-node message and the second minimum is determined by a configurable estimation weight factor based on the iteration and a correction factor based on the number of error bits in each hard decision. Compared to the original SMMS and VWMS algorithm, the simulation result shows the proposed ACMS algorithm reduce the performance loss in general by introducing only a little additional complexity.

LDPC codes; min-sum algorithm; single-minimum; estimation weight; channel adaptive

TN911.22

A

10.16280/j.videoe.2015.01.022

2014-06-04

【本文献信息】吴军，廖鑫，张小红.一种改进的LDPC码低复杂度最小和算法[J].电视技术,2015，39(1).