基于自回归移动平均模型的图像模糊消除机制

郭亚钢

(四川师范大学，四川 成都 610066)

基于自回归移动平均模型的图像模糊消除机制

郭亚钢

(四川师范大学，四川 成都 610066)

为了克服图像模糊消除算法不稳定与解模糊等难题，保证复原图像的细节信息清晰完整，并提高算法的运行效率，获取实时性，提出了神经网络融合自回归移动平均模型的图像模糊消除并行稳定机制。引入神经网络，基于突触权重系数，构造激活函数；再嵌入人工蜂群算法(Artificial Bees Colony,ABC)，并以神经网络的均方误差函数设计适应度方程，由ABC算法训练神经网络，利用优化后的神经网络来获取自回归移动平均模型的参数；再将自回归移动平均优化模型引入模糊图像，以同时识别模糊函数与模糊图像；并对模糊函数进行相关定义，以消除算法不稳定性与解模糊问题；再对模糊图像进行反卷积，消除模糊。借助仿真实验来测试该机制的相关性能，结果表明：与其他模糊消除算法相比，该机制的运行速度更快，时耗最短；且该机制更稳定，模糊消除效果更好，复原图像的细节信息清晰可见。

自回归移动平均优化模型；神经网络；激活函数；人工蜂群算法；模糊消除

随着计算机技术与交叉学科的不断发展和完善，图像处理在人们的日常生活中占据不可替代的地位[1]。图像模糊消除技术作为图像处理的一个非常重要的分支，在卫星遥感、医疗业及商业等领域中得到了广泛应用，成为当前的研究热点和焦点[2]。然而，由于成像设备、周围环境、天气以及人为因素，使得采集图像质量不佳，边缘模糊，易造成信息丢失，给图像的后续使用带来了巨大的负面影响。为了克服这个难题，能够清晰复原图像，诸多学者提出了图像模糊消除算法，以获得细节清晰的图像。其中，典型的去模糊算法为图像反卷积运算。它是一种图像增强算法，是对模糊图像的一种逆向变换。如李艳琴[3]等人引入动量矩和交替迭代法，求解图像频域和空间域的支持域，提出了一种改进的图像迭代盲反卷积算法来复原图像，并对其算法进行了实验验证，结果表明其算法具有较快的收敛速度，图像复原效果好。郭玲玲[4]等人借助多通道盲反卷积法求得点扩展函数，依据快速梯度投影算法进行优化求解，提出了受限全变差正则化的图像去模糊方法，并对其算法相关性能进行了测试，结果表明经该算法消除模糊后的图像与原始图像的结构相似度达到了0.982 4，复原效果好。Tam[5]等人引入Haar小波和Lucy-Richardson算法，提出了一种适用于正电子发射断层扫描图像的反卷积模糊消除算法，该算法可以增强图像的对比度，无需放大噪声等级，并对该算法进行了一系列的实验验证，结果显示其算法具有良好的去模糊效果，复原图像的细节信息较为清晰。为了有效消除运动模糊，段江永[6]等人根据图像中阶跃边缘区域与运动模糊核之间的内在关系，构造了边缘区域约束，提出了边缘区域约束引导的运动模糊图像复原机制，并对其算法进行了诸多实验验证，结果显示该算法简单，估计精度高，具有良好的去模糊效果。

尽管反卷积模糊消除算法能够取得良好的图像复原效果，但是当前的图像模糊消除算法大都集中于改善模糊消除效果，且都是非并行算法，忽略了算法的运行速度和计算代价，难以实现实时性；且这些算法不稳定，难以克服解模糊问题，其复原图像的细节信息清晰度有待进一步提高。

对此，为了使得模糊消除算法能兼顾良好的模糊消除效果和算法运行的实时性，本文引入神经网络，以并行模式运行，大大提高了算法的计算速度，并基于突触权重系数，构造激活函数；再嵌入人工蜂群算法(Artificial Bees Colony，ABC)，并以神经网络的均方误差函数设计适应度方程，由ABC算法训练神经网络，找出神经网络的最优权重值与阈值，实现全局最小，获取自回归移动平均模型的参数；引入自回归移动平均优化模型来同时识别模糊函数与模糊图像，对非线性模糊图像进行反卷积，有效解决了解模糊问题。最后借助MATLAB实验，通过与当前其他算法进行对比，测试了本文算法的相关性能。

1 基于自回归移动平均模型(ARMA) 表示的模糊图像及其模糊消除

任何一幅图像都可视为随机变量数组的样本函数，这种特性有利于开发图像处理技术。一个2D线性随机系统可产生失真图像的数学模型，可作为自回归移动平均模型(Autoregressive Moving Average Model，ARMA)的处理过程[7]；其中，自回归(Auto-Regressive，AR)模块决定了该系统的模糊函数。因此，盲图像反卷积问题可转变为ARMA的参数估算问题。确定ARMA的参数，有利于识别正确图像和模糊图像；而ARMA参数的估算可通过神经网络，联合经典的优化算法来获取。

将正确图像可被建模成一个2D 自回归过程

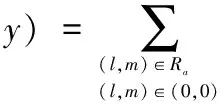
(1)

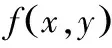
依据向量矩阵表示法，模型(1)可变为

f=Af+v

(2)

然而在实际的应用中，模糊函数带有局部性，当前的模糊消除机制中都忽略这个局限性。该函数对真实图像的影响可建模成一个2D FIR滤波器。线性模糊函数模型如下

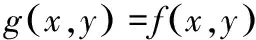
(3)

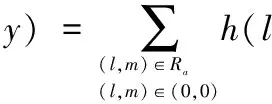
(4)

再次利用向量矩阵表示法，则模型(4)可表示为

g=Hf+η

(5)

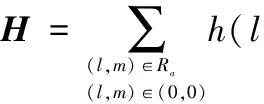
重排式(2)，代入式(5)，可得

g=H(I-A)-1+η

(6)

式中：I代表单位矩阵；A代表参数矩阵；η代表图像的零均值高斯附加噪声。

则根据式(6)，完整的基于ARMA模型的模糊图像如图1所示。从图1可知，盲图像反卷积问题就转变为AR参数a(l,m)∈Ra和MR参数h(l,m)∈Ra的估算问题。图1中Z1和Z2代表Z变换(Z-transformation)。

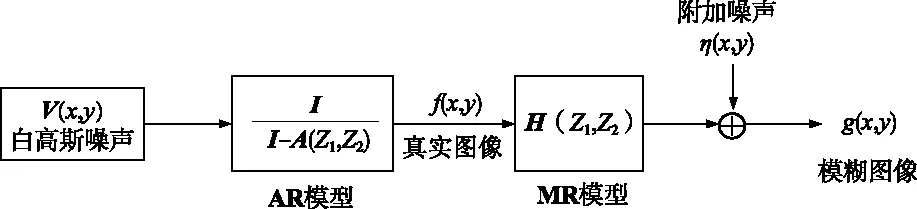
图1 基于ARMA模型的模糊图像

因此，一旦模糊函数h(l,m)被确定，则根据经典的线性图像复原技术就可得到真实图像。

然而，根据式(6)来估算a(l,m)和h(l,m)的缺陷就是计算复杂度高，估算算法不稳定，且没有唯一解。为此，本文引入二阶统计量方法[8]，对模糊函数进行如下定义：

1)该模糊函数值为正，则真实图像的均值保存在模糊过程中，即

(7)

通过这个定义，有效地解决了模糊解难题。

2)模糊函数值是对称的，且为零相位。该定义有效解决了估算算法的不稳定性，且保证有唯一解。

3)模糊函数有一个已知参数。可显著降低计算复杂度。其模糊消除机制见图2。

图2 本文模糊消除机制示意图

模糊消除步骤如下：

1)设计神经网络模型；

2)构造ABC算法的适应度方程，并对ABC算法进行初始化，再利用ABC算法训练神经网络；

3)将步骤2)得到的最优权重和阈值分别作为AR参数、MR参数；

4)根据步骤3)，构造ARMR模型，并对模糊图像与模糊函数进行识别；

5)利用反卷积技术对模糊图像进行复原，消除模糊，见图3。

图3 本文算法的模糊消除效果

从图3可知，经过本文模糊消除机制处理后，图像及其细节非常清晰，见图3b；对其局部(虚线方框)进行放大后，仍然是清晰可见，见图3c。

2 人工蜂群算法(ABC算法)

在人工蜂群算法中，ABC殖民地不断搜索丰富的人工食物源(对于一个特定的问题，找出最优解)[9]。为了应用ABC，首先将优化问题转变成找出最佳参数向量；然后人工蜂群随机发现一个初始解向量的种群，通过反复应用一种策略来改进：根据邻居搜索机制，向最优解靠近，放弃不良解。人工蜂群包括了3部分：1)雇佣蜂；2)跟随蜂；3)侦查蜂。

该算法的步骤如下：

1)初始化阶段

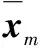
(8)

式中：lj和uj分别代表参数xmj的上、下边界；rand代表零均值的随机函数发生器。

2)雇佣蜂阶段

雇佣蜂搜索拥有更多花蜜的食物源vi，这些花蜜是与它们记忆中食物源xi相邻的；当它们找到一个相邻食物源时，开始估算它们的适应度。可根据如下函数来决定相邻食物源

vij=xij+φij(xij-xkj)

(9)

(10)

式中：fi为vi的成本；abs代表求取绝对值。

3)跟随蜂阶段

非雇佣蜂包括两个：跟随蜂和侦查蜂群。在ABC算法中，跟随蜂按照雇佣蜂提供的fitnessi获取概率值pi，并以此来择取食物源。因此，可使用基于选择机制的适应度值，如轮盘赌选择法。pi计算模型如下

(11)

式中：pi代表概率值；fitnessi代表适应度函数值。

在跟随蜂选择一个食物源xi后，通过式(9)来决定相邻食物源vi，并计算其相应的适应度值。由于在雇佣蜂阶段使用了贪婪选择机制，更多跟随蜂找到了更丰富的食物源，并因此产生正反馈行为。

4)侦查蜂阶段

由于侦查蜂群的解是被抛弃的，因此雇佣蜂无法通过预先设定好的轨迹来改善它的解，特别是ABC算法的用户及其所谓的“限制”。侦查蜂以随机方式来搜索新解。如果侦查蜂的解xi被抛弃，则其根据式(8)来产生新的解。

3 ABC算法优化神经网络(NN)

神经网络(Neutral Network，NN) 是一种并行结构的轻量非线性处理器。并行化、模块化以及动态自适应是其3个典型的计算特性；其多层感知器(Multilayer Perception，MLP)由不同的层构成：1)输入层；2)隐蔽层；3)输出层，见图4。

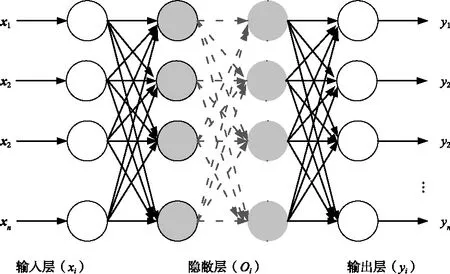
图4 多层神经网络示意图

图4中的这些层都是基于一些与前反馈环节有关的神经处理单元来进行的，见图5。

图5 一个神经网络单元信息处理示意图

上述单元都进行相同步骤：1)由式(12)输入总权重；2)根据这些权重，构造激活函数，根据式(13)输出实际值yi。

对于输入层xij，其隐蔽层节点的输入值为

(12)

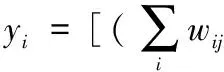
(13)

式中：yi代表处理单元的输出值；wij代表突触权重系数；bj代表模型(13)的阈值。

逆向传播机制BP(Back Propagation)作为一个有效的学习规则，已经成功用于找出神经网络的最优权重和基础值；使用ABC算法，通过所有的权重矩阵元素wij来定义每个食物源向量；且其最优解为误差函数的适应度值。在BP和ABC算法同时达到相等的误差精度，ABC算法的计算复杂度更低，运行速度更快。因此，本文引入ABC算法，以训练神经网络，最大限度减小NN单元的均方误差函数，并用多层NN结构来表述能够同时识别模糊函数与模糊图像的ARMR模型。本文所采用的多层神经网络模型见图6。由于本文的NN结构的输入端为高斯噪音，故以均方误差函数来设计ABC算法的适应度

(14)

式中：N为训练标本；qi代表预期输出值；yi代表实际输出值；MSE代表均方误差函数。

图6 神经网络结构

具体训练步骤如下：

1)选定训练样本N，根据式(12)计算各层间的突触权重系数wij。

2)再根据式(13)计算样本的输出值yi。

3)依据式(14)计算出MSE。

4)利用ABC算法训练NN；若MSE≤ε(e-7)，则训练结束，输出此时的权重wij和阈值bj；否则返回步骤1)，继续执行。

5)将最优解wij和bj分别作为AR参数、MR参数。

经过ABC算法训练神经网络后，得到最佳的MSE，见图7。从图中可以看到，在迭代35次时，就开始收敛，稳定MSE为0.87×10-7，误差非常小。

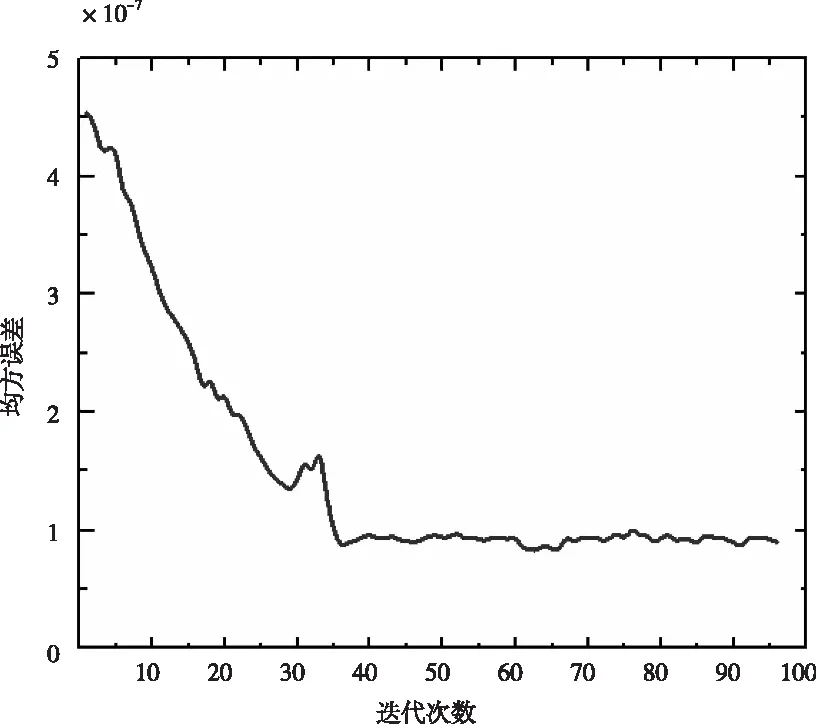
图7 ABC算法训练神经网络过程中的MSE变化

4 仿真结果与分析

为了凸显本文机制性能的优异性，将文献[10]、文献[11]视为对照组，分别记为A、B机制。在Inter 3.5 GHz 双核CPU、16 Gbyte的内存的私人机上进行实验。设置ABC算法的种群规模N=50，选择概率值p=0.3，迭代次数113；神经网络模型见图6。

实验对象见图8a所示，尺寸为228×228；且向该图施加了30%的高斯白噪声。从信噪比PSNR、计算效率以及局部放大细节清晰视觉效果3方面来测试。PSNR的计算模型[10]为

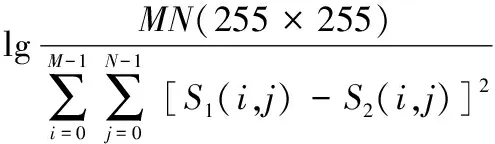
(15)

式中：PSNR为模糊消除图像的信噪比；MN为图像尺寸；S1(i,j)代表正确图像在位置(i,j)的灰度值；S2(i,j)代表模糊消除图像在坐标(i,j)的灰度值。

图8 不同机制的模糊消除效果

图8为不同模糊消除机制处理后的复原图像视觉效果。从图中可知，3种不同的模糊消除机制的去模糊效果相差无几，图像细节都清晰，没有明显的噪声。

为了量化3种不同机制的去模糊质量，本文测试它们的PSNR，结果见图9。从该图中可知，3种机制复原图像后的稳定PSNR都很接近，分别为32.47 dB(本文机制)、32.21 dB(A机制)、32.52 dB(B机制)；但是3种机制存的计算效率存在明显的差异，本文机制的运行速度最快，在13 s时，就进入了稳定状态；而A、B机制分别需要25 s、32 s。主要原因是本本文机制设计了ARMR神经网络模型来同时识别模糊图像和模糊函数，以并行模式进行复原；而其他两种机制过分专注于改善模糊消除效果，以单一通道进行复原。可见，本文模糊消除机制具有较快的计算效率。

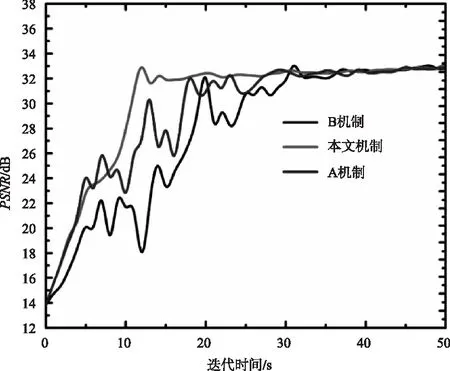
图9 不同模糊消除机制复原图像的信噪比

另外，从图9中也可看到，本文机制的稳定性较好，在进入稳定PSNR前，其波动程度要显著低于A、B机制。这也表明本文模糊消除机制的稳定性较好。原因是本文机制对模糊函数进行了限制定义，使其函数值是对称的，且为零相位。

去模糊图像局部放大视觉效果如图10所示。放大位置如图10a虚线框框所示。从图中可以看到，本文机制的模糊消除效果最佳，局部放大后，图像边缘信息以及细节非常清楚，见图10b所示；而经过A、B机制去模糊处理后，局部放大视觉相接近，去模糊质量较好；通过对比图10c所示部分细节，可知A、B机制的模糊消除效果不如本文机制。

图10 不同模糊消除机制对应的局部放大视觉效果

5 结论

针对当前的模糊消除机制专注于改善复原效果，而忽略了运行速度，导致计算效率较低，以及模糊消除机制不稳定等不足，本文引入神经网络和人工蜂群算法计算自回归移动平均模型的参数；再将回归移动平均模型引入模糊图像；并对模糊函数进行相关定义；最终提出了基于自回归移动平均模型的图像模糊消除并行稳定机制。该机制以并行模式进行复原，兼顾了高的复原质量和高运行速度。仿真实验验证了本文模糊消除机制的优越性，结果表明：与其他模糊消除算法相比，该机制的运行速度更快，时耗最短；且模糊消除机制更稳定，去模糊效果更佳，复原图像的细节信息清晰可见。

[1]王鹏，王明泉. 基于模型各向异性的骨科CT图像去噪处理[J]. 电视技术，2013，37(7)：4-5.

[2]程芳瑾，杜晓俊，马丽. 基于Retinex的低照度图像增强[J]. 电视技术，2013，37(15)：4-6.

[3]李艳琴，张立毅，孙云山. 一种改进的图像迭代盲反卷积算法[J]. 计算机工程，2012，38(8)：204-206.

[4]郭玲玲，张立国，吴泽鹏，等. 基于受限全变差正则化的遥感图像去模糊方法[J]. 激光与光电子学进展，2013，32(11)：461-465.

[5]TAM N，LEE J，HU C. A Haar-wavelet-based Lucy-Richardson algorithm for positron emission tomography image restoration[J]. Nuclear Instruments and Methods in Physics Research A，2011(124)：122-127.

[6]段江永，孟高峰，向世明. 边缘区域约束引导的运动模糊图像复原[J]. 计算机辅助设计与图形学学报，2012，24(8)：1038-1045.

[7]TEKALP A， SEZAN M. Identification of image and blur parameters for the restoration of noncausal blurs[J]. IEEE Trans. Acoustics，Speech，Signal Processing，2010，34(4)：963-972.

[8]闫晓波，王士同，郭慧玲. 基于Parzen窗的高阶统计量特征降维方法[J].智能系统学报，2013，8(1)：1-10.

[9]冀俊忠，魏红凯，刘椿年. 基于引导素更新和扩散机制的人工蜂群算法[J].计算机研究与发展，2013，50(9)：232-236.

[10]黄玉飞，齐和平，张文斌，等. 基于小波系数和LS-SVM的图像去噪[J].电视技术，2013，37(1)：12-16.

[11]ZHOU X，ZHOU F，BAI X. A boundary condition based on deconvolution framework for image deblurring[J]. Journal of Computation and Applied Mathematics，2014，26(1)：14-29.

Study on Image Deblurring Mechanism Based on Autoregressive Moving Average Model

GUO Yagang

(SichuanNormalUniversity，Chengdu610066，China)

In order to overcome the unstable with ambiguity blurring problem of these algorithm，as well as guarantee the clear and complete detail information of restoration image，and improve the computation speed of current image deblurring algorithm to achieve the goal of real time，the real-time stable mechanism for image deblurring based on the autoregressive moving average model is proposed. The active function is constructed by introducing the neural network and basing on the synaptic weights coefficient；then the fitness function is designed by the mean square error function of neural network；and embedding the artificial bee colony algorithm (ABC-Artificial Bees Colony) to train the neural network for finding the optimized weight value of neural network as well as the bias of active function to achieve global minimum；finally，the autoregressive moving average optimized model is designed to simultaneously identify fuzzy functions and fuzzy image to deconvolution the nonlinear deblurring image for eliminating the fuzzy. The performance of this algorithm is tested by simulation experiments. The results show that compared with other deblurring algorithms，the running speed of this mechanism is faster，and time consuming is the shortest；as well as the deblurring effect is the best，the detail information of restoration image is clearly visible.

weighted autoregressive moving average optimized model；neural network；active function；artificial bee colony algorithm；deblurring

四川省人工智能重点实验室开放基金项目(2011RYJ04)；四川省教育厅自然科学重点项目(09ZA120)

TN911.73；TP391

A

10.16280/j.videoe.2015.01.002

2014-12-08

【本文献信息】郭亚钢.基于自回归移动平均模型的图像模糊消除机制[J].电视技术,2015，39(1).

郭亚钢(1981— )，硕士，主要研究领域为图像处理。

责任编辑：时 雯