基于稀疏正则化结合NLS的超分辨率图像重建
王华君,孟德建,姚 湘
(无锡太湖学院 工学院,江苏 无锡 214064)
基于稀疏正则化结合NLS的超分辨率图像重建
王华君,孟德建,姚 湘
(无锡太湖学院 工学院,江苏 无锡 214064)
为了保持高光谱(HS)超分辨率重建过程中的频谱一致性和边缘锐度,提出一种基于空间谱结合非局部相似性的超分辨率重建算法。首先,使用HS图像生成模型,采用稀疏正则化解决全色(PAN)图像和HS图像重建的病态问题求逆;然后分析了从高空间分辨率到低空间分辨率数据生成的丰度系数映射;最后利用非局部相似性,设计空间谱联合正则化项。使用机载可见光/红外成像光谱仪(AVIRIS)和Hyperion图像测试该算法,实验结果表明,提出的算法重建图像在PSNR,SSIM和FSIM方面明显高于其他优秀算法,在SAM和ERGAS方面明显低于其他优秀算法,在光谱失真方面丢失最少,仅有2%~3%,低于其他算法30%左右,且重建效果更加清晰自然。
高光谱;超分辨率重建;非局部相似性;稀疏正则化;全色图像
最近几十年,高光谱(hyperspectral, HS)[1-2]成像的理论和技术发展非常迅速,应用极其广泛,如地形分类、矿物检测和勘探、遥感制图、环境监测,以及军事监视等[3]。由于仪器限制和不完美成像光学器件,HS传感器谱相元分辨率很高,但对应的物分辨率却很有限,HS图像难以获取高分辨率数据,大大降低了民用和军事领域所需的检测和识别性能[4]。因此,如何提高HS数据空间分辨率成为一项重要课题。
文献[5]以最大后验概率(Maximum Posterior Probability, MAP)为理论基础,利用感兴趣类别端元将原始高维数据映射到低维空间,以MAP为理论基础,给出HS图像重建的MAP模型。文献[6]结合局部和非局部相似性约束,同场景的高分辨率场景彩色图像的自适应权重滤波,在频谱一致性方面表现并不好。高分辨率图像像素空间位置可以从HR PAN图像获得或从相应的HR HS图像了解到。文献[7]提出一种基于混合信息和总变差(Total Variation, TV)最小化来产生HR HS图像的算法,但TV正则化会导致图像边缘纹理细节的模糊和丢失。文献[8-9]提出了其他基于软分类输出的超分辨率映射算法,进一步改善了重合图像的质量,然而,其重构结果依赖于分类的准确性。
为了获得更好的重建效果,本文提出了一种基于非局部相似结合稀疏正则化的HS图像超分辨率算法,在超分辨率过程中合并了分离结果和PAN信息,通过从PAN图像中提取类似的小块来预测HS图像中的小块,即所预期的表示误差很小,这与稀疏表达的超分辨率思想[10-11]很像。将稀疏正则化和非局部相似性(Non-Local Similarity, NLS)有效结合,有助于保留边缘清晰度和频谱一致性,且可以很好地抑制噪声。
1 非局部相似性和稀疏融合
HS超分辨率问题是一种典型的病态问题求逆,由于LR图像数量不足,在超分辨率重建算法中,解决方案不唯一,正则化算法是进一步稳定病态问题求逆[12]的有效算法。
1.1 空间谱联合非局部结构相似
HS图像采集过程可以参照文献[12]建模
Y=WHX+v
(1)
式中:Y表示LR HS数据;X表示HR HS数据;W表示空间谱下采样算子;H表示模糊滤波器引起的空间谱,例如大气湍流;v是加性噪声。
X可以通过式(2)来估算
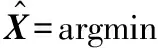
(2)
这是极为病态的,因为对于给定的输入Y,无限多的图像X可能满足上述重建约束。由于在观察的场景中有许多非局部重复物质,它们具有相似的光谱和空间结构,利用非局部重复可以提高图像重建的质量。受到非局部均值滤波成功用于图像去噪和检索的启发,引入了非局部自相似超分辨率过程,以充分利用重复,利用从HR和LR HS数据生成的丰度映射系数中的非局部相似引入空间谱联合结构相似。
HR HS数据光谱混合模型[12]可表示为
(3)

假定端元在空间分辨率增强后不变化,当式(1)中HR数据X和LR数据Y表示相同场景时,相应的端元应该相同。基于式(1)中的HS数据模型,LR数据Y可由下采样和空间模糊滤波器获得,该LR HS光谱混合模型可表示为
(4)

对于每一个局部小块Yi,基于端元比例相似在整个图像Y寻找相似小块,小块Yji可以选择作为Yi的一个相似小块,如果
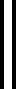
(5)

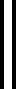
(6)

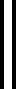
(7)
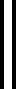
(8)
I是单位矩阵,B设置如下
通过基于式(2)结合非局部结构相似性光谱和空间域到超分辨率恢复过程,得到下列基于空间谱联合非局部结构相似性的HS超分辨率问题

(9)

1.2 HS和PAN图像稀疏融合
HS和PAN图像融合的目的是通过整合具有不同空间和光谱分辨率数据所传递信息,各种图像融合技术利用互补空间/频谱分辨率特性来产生HR HS观察[7]。使用Y表示LR HS数据,使用P表示HR PAN图像,融合过程可表示为
Z=f(T1(Y),T2(P))
(10)
式中,f是融合规则,T1和T2代表相应的变换,传统上,T1和T2可以是小波变换、曲波变换或一些其他多尺度技术,通过预定义的融合规则, PAN的空间结构注入到HS数据。但是这些算法都无法避免光谱失真。作为一种强大的统计图像建模技术,稀疏编码可以利用训练过的字典原子项表示结构信息。
根据文献[2]提出的HS稀疏融合模型和稀疏表示模型,HR图像X可估计为
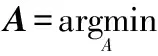
(11)
作为一种稀疏融合技术,文献[13]设计了线性退化模型,涉及HR图像到LR MS图像和PAN HR图像,降解过程可视为压缩传感,l1-范式用作融合MS和PAN图像的正则项,频谱一致性由PAN图像通过MS图像的线性组合近似的假设来保证。仅有彩色图像的情况下,获得HS和PAN数据的组合权重很困难,此时很难获得满意的恢复结果。
1.3 超分辨率重建
空间谱联合非局部HS超分辨处理仅基于低空间HS图像,虽然这种算法能保持光谱的一致性,但是在超分辨率过程中无额外信息引入。稀疏正则化过程将保留边缘锐度,式(11)表示HS和PAN图像融合过程,通过引入PAN信息,边缘锐度保留,除去空间域中噪声。式(9)表示基于空间谱联合非局部结构相似性的超分辨率,这种重建算法提供了良好的光谱一致性。通过组合式(9)和式(11),PAN图像信息集成到非局部HS超分辨率处理中,得到最终的超分辨率重建问题

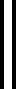
(12)
为了求解式(12),引入一个临时变量V,假设V≈X,则可以得到

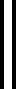
(13)
超分辨率算法如算法1所示。
算法1:基于空间谱联合非局部相似的HS超分辨率算法
输入:LR HR图像Y,由与Y不相关的HR PAN训练过的字典Φ
使用非局部权重初始化B,使用Y的下采样初始化X
初始化μ,λ,η,γ
Loops begin:
相对于A的优化

相对于V的优化

相对于X的优化

Loops end
停止准则可设计为固定迭代次数、运行时间、第T次迭代和第T-1次迭代之间的误差。
2 实验
将本文算法与4种优秀算法进行比较,包括:基于光谱调节的算法[2](SRSR)、基于改进的MAP HS图像超分辨率算法[5](MMAP)、端元TV-正则化算法[7](ETV)和基于稀疏块分类表示的算法[11](SRCIP)。第一个实验,PAN图像光谱范围覆盖HS数据的跨度,第二个实验中,PAN图像的光谱范围不覆盖HS数据的整个跨度。使用5种量化指标,即峰值信噪比(PSNR)、结构相似性(SSIM)指标、功能相似性(FSIM)指标[2]、光谱角映射(SAM)和相对全局合成维度误差(ERGAS)。
2.1 评估指标
评估空间分辨率增强性能的最常用指标是PSNR,每个频带信号峰值可以显著改变,这使得该指标偏向具有更高能量的频带,第b个频带的PSNR定义为
(14)
式中:Speak,b第b个频带信号峰值;MSEb为地面实况与估计的第b个频带之间均方差。
(15)
式中:M和N表示超分辨图像中行和列的数目;ISR,b为所估计的分辨率增强图像;Io,b为原始HR图像。
PSNR可以用来评估重建质量,结构信息用于表示具有较强相互依赖的像素在空间上接近,这些依赖关系携带关于场景中对象结构的重要信息。2幅普通大小为N×NHS图像x和y之间的量度为
(16)
式中:μx是x的平均值;μy是y的平均值;vx是x的方差;vy是y的方差;vxy是vx和vy的协方差;C1=(k1L)2和C2=(k2L)2是2个变量,用于稳定具有弱分母的除法;L为像素值的动态范围,默认k1=0.01,k1=0.03。
文献[14]提出了一种新的FSIM指标,用于完整参考图像的质量评估,在评估过程中同时使用相位一致性(PC)和梯度幅度(GM),HS图像x和y之间的FSIM指标可定义为
(17)
式中:Ω意味着整个图像空间域,PCm(z)=max{PCx(z),PCy(z)},其中PCx(z)是对于图像x给定位置z的相位一致性,SL(z)为对于给定位置z的GM。
SAM通过从源图像y和增强图像x每个像素构建的2个向量之间的绝对角度来影响光谱失真。令μx和μy分别表示x和y像素的频谱向量,HS图像x和y之间的SAM由下式计算
(18)
ERGAS指标可用来量化不同超分辨率结果的光谱和空间质量,该指标定义为
(19)
式中:α为放大倍数;P为光谱带的数量;MHSi为每个频带的平均。对于完全增强的图像,ERGAS也应该是零。
2.2 AVIRIS数据集
AVIRIS数据集中的HS图像由AVIRIS传感器收集,在370~2 510 nm范围内有224个光谱带、400×400像素和 3.5 μm 空间分辨率。图像使用ENVI的FLASH模块常压校正,产生反射率图像,除去噪声频带后,共有189条频带保留。在这个场景中,有人造对象(道路、屋顶、和飞机)、草地、树木,人造对象有锋利的边缘,而草地和树木有丰富的质感。在实验中,首先对原始图像在1.6标准偏差下运用截短的7×7高斯内核,然后由因子为3的均值滤波器进行下采样,产生退化的LR PAN和HS图像。式(13)中,λ和η是自由参数,λ用于调整l1-范式的贡献,η用于平衡非局部正则化贡献,参照文献[7]和文献[11],λ和η在所有实验中均设为:λ=0.077 5,η=0.141 4。
为了生成字典,使用具有0.7 m空间分辨率的QuickBird全色图像,从http://glcf.umiacs.umd.edu/data/quickbird/网站上下载20幅PAN图像,它们不相关,并且不与测试图像重叠。这些图像是由因子为3的均值滤波器下采样,以便拥有与增强HS数据相似的空间分辨率。随后,随机取样 10 000 个原始8×8小块,利用这些小块,由K-SVD算法训练字典, OMP算法用于稀疏编码。图1所示为用于生成字典的PAN图像。
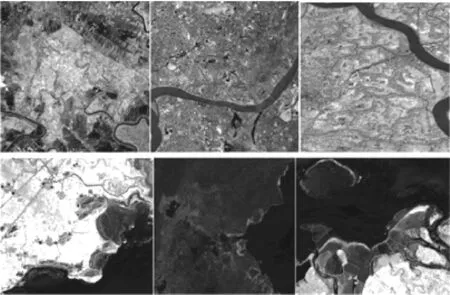
图1 用于重建字典的PAN图像
图2所示为基于SRSR算法、基于MMAP算法、基于ETV算法、基于SRCIP算法和本文算法(SRNS)的空间超分辨率重建结果。仅显示出了中心在675和2 018 nm的2个光谱带的结果。图3所示为图2的细节。PSNR,SSIM和FSIM的量化评估如图4所示。表1显示了不同算法的SAM和ERGAS值。本文算法SRNS的各个评估指标(PSNR,SSIM,FSIM,SAM和ERGAS)均优于其他超分辨率算法。此外,从图2~图3可以看出,利用本文算法重建后的飞机、道路、屋顶、草地比其他重建算法更清晰,边缘也更加尖锐。

图2 San Diego数据库的空间分辨率重建结果

图3 图2中的细节

对比项MMAPSRCIPETVSRSRSRNSSAM51335602405143493231ERGAS49315731420143192969

图4 San Diego数据集由不同空间分辨率增强算法得到的结果
本文算法的一个主要优点是,它为每个块从训练的字典中选择原子项,稀疏调整确保这些小块可以通过字典中最相关的原子项来表示给定的HS数据,在整个观察到的场景中有许多非局部重复物质,它们具有相似的光谱和空间结构,此类非局部重复信息对改善重建质量有效。本文算法联合利用了光谱和空间信息,基于从原始低空间分辨率HS图像提取的端元,因此,最新重建的HR HS数据也良好保留了源图像的空间和光谱信息。
2.3 Hyperion数据集
Hyperion图像为307行×307列,共有220条频带,空间分辨率为30 μm。AL1 PAN图像用来训练字典,AL1 PAN图像的空间分辨率为10 m,Hyperion和AL1数据可从网站上http://earthexplorer.usgs.gov/下载。Hyperion和AL1数据也由因子为3的均值滤波器下采样得到,为了训练辞典,从10幅 AL1 PAN图像随机抽取10 000个原始小块,其与Hyperion图像无关。
图5所示为本文算法与其他方法在第41频带(中心波长为762.6 nm)空间分辨率增强的比较结果。图6显示了与图5对应的细节。视觉比较表明,本文算法比其他方法产生更尖锐的边缘,且增强了图像的纹理。图7和表2中相应的量化指标表明本文算法最优。

图5 Hyperion数据库的空间分辨率增强结果

图6 图5结果的细节

图7 Hyperion数据集上由不同空间分辨率增强算法得到的结果

对比项MMAPSRCIPETVSRSRSRNSSAM43494721363337403011ERGAS52095140343332702649
3 结语
本文提出了基于稀疏表示和空间谱联合结构相似的HS和PAN图像融合算法,主要贡献是在融合过程中利用非局部端元丰度映射,采用稀疏正则化来解决PAN和HS图像融合的病态问题求逆过程和设计空间谱联合正则项,使融合结果更自然。2类不同的HS数据集上的实验结果表明,本文算法明显优于传统分辨率重建算法。
由于本文算法计算复杂度较高,未来将利用优化代码,使其能在多核处理器上迭代以减少计算时间。
[1] 史云静, 虞涛, 朱秀昌. 基于训练集分层的图像超分辨率重建[J]. 电视技术,2012,36(19): 18-22.
[2] ZHAO Y, YANG J, ZHANG Q, et al. Hyperspectral imagery super-resolution by sparse representation and spectral regularization[J]. EURASIP Journal on Advances in Signal Processing,2011,17(1):1-10.
[3] ZHANG H, YANG Z, ZHANG L, et al. Super-resolution reconstruction for multi-angle remote sensing images considering resolution differences[J]. Remote Sensing,2014,6(1):637-657.
[4] ZHANG H, ZHANG L, SHEN H. A super-resolution reconstruction algorithm for hyperspectral images[J]. Signal Processing,2012,92(9): 2082-2096.
[5] 赵妍. 基于MAP的高光谱图像超分辨率方法研究[D]. 哈尔滨:哈尔滨工程大学, 2010.
[6] 杨宇翔, 曾毓, 何志伟,等. 基于自适应权值滤波的深度图像超分辨率重建[J]. 中国图象图形学报,2014,19(8) : 112-118.
[7] EASON D T, ANDREWS M. Total variation regularization via continuation to recover compressed hyperspectral images[J]. IEEE Trans. Image Processing: a Publication of the IEEE Signal Processing Society,2015,24(1): 284-293.
[8] SU Y F, FOODY G M, MUAD A M, et al. Combining Hopfield neural network and contouring methods to enhance super-resolution mapping[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2012, 5(5):1403-1417.
[9] MUAD A M, FOODY G M. Impact of land cover patch size on the accuracy of patch area representation in HNN-based super resolution mapping[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2012,5(5): 1418-1427.
[10] ZHANG H, LI J, HUANG Y, et al. A nonlocal weighted joint sparse representation classification method for hyperspectral imagery[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2014,7(6):2056-2065.
[11] 练秋生, 张伟. 基于图像块分类稀疏表示的超分辨率重构算法[J]. 电子学报,2012,40(5):1121-1127.
[12] ZHAO Y, YANG J, ZHANG Q, et al. Hyperspectral imagery super-resolution by sparse representation and spectral regularization[J]. EURASIP Journal on Advances in Signal Processing,2011,2011(1):1-10.
[13] LI S, YANG B. A new pan-sharpening method using a compressed sensing technique[J]. IEEE Trans. Geoscience and Remote Sensing,2011,49(2):738-746.
[14] WANG Y H, QIAO J, LI J B, et al. Sparse representation-based MRI super-resolution reconstruction[J]. Measurement, 2014,47(6):946-953.
王华君(1979— ),讲师,硕士,主研图像处理与模式识别等;
孟德建(1979— ),讲师,博士,主研视频和图像处理、移动互联感知等;
姚 湘(1984— ),女,讲师,硕士,主研图像分析、图像处理等。
责任编辑:闫雯雯
Super-Resolution Image Reconstruction Based on Fusion of Sparse Regularization and NLS
WANG Huajun, MENG Dejian, YAO Xiang
(SchoolofEngineering,TaihuUniversityofWuxi,JiangsuWuxi214064,China)
To maintain spectral consistency and edge sharpness during the processing of super-resolution reconstruction of hyperspectral (HS) images, a joint super-resolution algorithm based on fusion of space spectrum and non-local similarity (NLS) is proposed. Firstly, HS images are used to generate model, and sparse regularization is used to solve the inversion of the ill problem of the reconstruction of panchromatic (PAN) images and HS images. Then, the generated map of abundance coefficients between spatial high resolution and low resolution is analyzed. Finally, space spectrum joint regularization term is designed by non-local similarity. The proposed method is tested with Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) and Hyperion images. Experimental results show that the reconstructed image by this paper is obviously higher than other good algorithms on PSNR, SSIM and FSIM, and lower than other outstanding algorithms significantly on SAM and ERGAS. Proposed algorithm misses the least spectral with only 2% to 3%, which is 30% lower than other algorithms, and the reconstruction results are more natural and clear.
hyperspectral; super-resolution reconstruction; nonlocal similarity; sparse regularization; panchromatic image
江苏省高校自然科学研究项目(14KJD520009)
TP391.4
A
10.16280/j.videoe.2015.17.007
2015-03-10
【本文献信息】王华君,孟德建,姚湘.基于稀疏正则化结合NLS的超分辨率图像重建[J].电视技术,2015,39(17).

