基于块分类稀疏表示的图像融合算法
陈利霞,李 子,袁 华,欧阳宁
(桂林电子科技大学 a. 广西高校图像图形智能处理重点实验室;b. 数学与计算科学学院;c.广西密码学与信息安全重点实验室;d.信息与通信学院,广西 桂林 541004)
基于块分类稀疏表示的图像融合算法
陈利霞a,b,c,李 子d,袁 华d,欧阳宁d
(桂林电子科技大学 a. 广西高校图像图形智能处理重点实验室;b. 数学与计算科学学院;c.广西密码学与信息安全重点实验室;d.信息与通信学院,广西 桂林 541004)
针对基于单一字典训练稀疏表示的图像融合算法忽略图像局部特征的问题,提出了基于块分类稀疏表示的图像融合算法。算法是根据图像局部特征的差异将图像块分为平滑、边缘和纹理三种结构类型,对边缘和纹理结构分别训练出各自的冗余字典。平滑结构利用算术平均法进行融合,边缘和纹理结构由对应字典利用稀疏表示算法进行融合,并对边缘结构稀疏表示中的残余量进行小波变换融合。实
块分类;稀疏表示;图像融合
图像融合是将同一场景来源不同的多幅源图像的互补信息综合起来,以获得该场景更加准确、全面和细致描述的一种图像处理技术。它在计算机视觉、医学以及航空航天等领域中都有广泛的应用。图像融合算法主要有基于空域的(加权平均、主元分析等)和基于变换域的(小波变换、Contourlet变换[1]等)。这些融合算法的优点是速度快,但是容易丢失图像的边缘等细节信息,从而影响融合图像的清晰度。
稀疏表示(Sparse representation,SR) 算法作为一种有效的表示模型,克服了以上问题得到较理想的融合效果,成为近年来的研究热门。Yang B[2]提出一种基于过完备字典稀疏表示的图像融合算法,利用DCT字典建立稀疏分解模型,但DCT字典的适应性不强,运算复杂度高;陈垚佳[3]提出从待融合图像中随机抽取训练样本集,采用K-SVD法对样本集训练得到过完备字典,相比DCT字典能够更接近待融合图像特征,但是待融合图像本身存在信息缺失的问题,容易导致字典出现信息缺损;余南南[4]利用K-SVD法对图像库构成的样本集进行训练得到K-SVD字典,能更好表示图像特征,适应性强,并根据稀疏系数非零性分离相似特征和相异特征分别进行融合,以提高融合图像中相异特征的清晰度。虽然这些算法在字典训练上都有所改进,但是单一字典容易忽略图像的局部特征,不能有效表示图像块结构特性的差异。
针对这一问题,提出了一种基于块分类稀疏表示的图像融合算法。它将图像的子块划分为平滑、边缘和纹理3种结构。对于具有明显边缘和纹理的图像块,分别训练各自的字典进行稀疏表示,以获取更加精确的稀疏系数。平滑块直接利用算术平均法进行融合,减少了运算复杂度;边缘和纹理结构通过分类稀疏表示的方法进行融合,并对边缘结构稀疏表示中的残余量进一步采用小波变换进行融合,保证了信息的完整性。实验结果证明, 本文算法在融合图像的主观评价和客观评价指标上均有显著改进, 并且算法速度也有提高。
1 基于稀疏表示的图像融合算法
稀疏表示的理论描述如下,假设D=[d1,d2,…,dN]∈RK×N为一个过完备集,对于给定的观测信号x,可通过字典中原子的线性组合来表示,即对任意的x∈Γ,存在s∈RN,使得x=Ds。稀疏表示的一般描述为求解式(1)
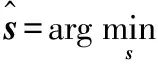
(1)
式中:ε为误差值。基于稀疏表示的图像融合算法,其本质为待融合图像基于过完备字典对每一个像素域进行稀疏表示再融合、重构的方法[5-7]。其框架如图1所示,方法步骤如下:
1)将严格配准的待融合图像归一化,再进行滑动(sliding)分块处理,并把每个图像子块像素拉直成一维列向量v,得到列向量矩阵V。
2)将每个子块列向量v在冗余字典D上利用OMP进行稀疏编码,获得稀疏系数a。
3)把对应的稀疏系数a按照一定规则融合得到重构系数A,再结合系数A与冗余字典D重构出融合结果图像。

图1 基于稀疏表示的图像融合算法的框架
基于稀疏表示的图像融合相比传统算法融合效果好,但单一字典的稀疏表示往往忽略了图像的局部特征。针对这一问题,提出了一种基于块分类稀疏表示的图像融合算法,它将图像的子块划分为平滑、边缘和纹理结构三类,对边缘和纹理结构分别训练相应字典进行稀疏表示。
2 基于块分类稀疏表示的图像融合算法
2.1 块分类
根据待融合图像的局部结构特性,对分块得到的图像子块进行分类。图像f可分为平滑结构fs、边缘结构fe和纹理结构ft。分类方式如下:
1)平滑结构。根据图像块之间包含的图像信息量不同,图像子块可分为平滑结构和细节模型。检测图像的信息量高低,常用的测量函数有方差(Variance)、梯度(Gradient)、空间频率(SF)以及改进拉普拉斯能量和等。文献[8]指出,在同等条件下,方差计算速度快且有较好效果,够有效区分平滑结构和细节结构。方差d计算公式为
(2)

(3)
式中:dA和dB分别为待融合图像A和B对应位置子块的方差值。
2)边缘结构和纹理结构。经过以上划分,图像块分为平滑结构和细节结构。本文利用图像子块梯度场的指向性将细节结构分为边缘结构和纹理结构。通过对图像块梯度场奇异值分解(SVD),估计图像块的局部方向性,其中指向一致性强的作为边缘结构,指向性弱的作为纹理结构。


(4)
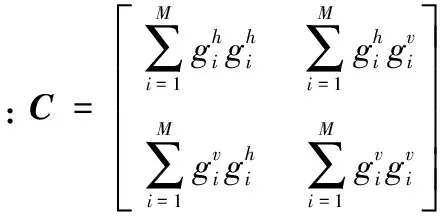
图像块梯度场主方向v是G最小奇异值所对应的奇异分量。对G奇异值分解
G=UΔVT
(5)
式中:V是2×2的正交矩阵,第一列v1代表图像块梯度场的主方向;矩阵Δ大小为M×2。可得G的奇异值为s1和s2,s1代表梯度场主方向上的能量,s2代表与梯度场主方向正交方向上的能量。
设定参数c判定边缘,则c为
(6)
根据上式计算细节结构中每个图像块的c,设定阈值,μ2若待融合图像对应位置子块的c值都小于等于μ2,则为纹理结构ft;否则子块为边缘结构fe。
(7)
式中:cA和cB分别为待融合图像A和B对应位置子块的c值。
2.2 基于块分类的字典训练
基于块分类稀疏表示的图像融合选择K-SVD法训练字典,训练可离线操作。字典训练过程为先将待训练样本进行分类,然后对边缘结构和纹理结构块分别进行训练。
首先,从标准图像库中随机选取N个n×n大小的待训练图像块,根据图像块的方差d和选取的阈值μ1区分出平滑结构块和细节结构块。
其次,利用式(4)~(7)将细节结构块区分为边缘结构和纹理结构。其边缘结构块构成训练样本集Xe,纹理结构块构成训练样本集Xt。
最后,利用K-SVD算法对样本集Xe和Xt分别训练出边缘结构fe和纹理结构ft对应的冗余字典。设定稀疏度为T,冗余字典中原子数为R,稀疏系数为θ={θi},通过迭代解决如下优化问题

(8)
对DCT字典通过以上方法训练,可得到自适应边缘、纹理冗余字典。相对于单一字典该方法改进了原字典的结构,能够获得更有效反映图像局部结构特性的冗余字典。
2.3 图像融合
平滑结构fs包含的信息量少,像素值变化平缓,用算术加权平均法进行融合就能有较好的效果,且算法简单,可减少运算复杂度。权系数选取ω1=ω2=0.5。
边缘结构fe和纹理结构ft利用各自训练的冗余字典进行稀疏表示的图像融合。结构块利用OMP算法获得相对应的系数αA和αB。融合规则为选取稀疏度较低的系数a,当稀疏度一致时,则用l1范数进行系数选取。如式(9)所示
(9)
在稀疏编码中,OMP求解式(1)是一种循环逼近的算法,残余量衰减到一定程度就会很难搜索到与残余量相匹配的原子,因此衰减后的残余量会引起部分源图像信息的丢失,从而影响融合效果。本文算法对边缘结构稀疏表示的OMP残余量进行了小波变换融合,再将融合的残余量加到融合图像中。残余量r为

(10)
可得到残余矩阵RA和RB。先对残余矩阵进行小波分解,再采取高频系数绝对值取大和低频系数算术平均的融合规则,最后通过逆小波变换得到融合的残余量R。
基于块分类稀疏表示的图像融合算法步骤流程如图2所示。

图2 基于块分类稀疏表示的图像融合算法框图
步骤1,分块。对源图像A,B进行n×n大小的滑动分块,分别得到(N+n-1)×(M+n-1)个图像子块。
步骤2,块分类。利用对应子块的方差d区分平滑结构块和细节结构块,d都小于等于阈值μ1的子块属于平滑结构,否则为细节结构;计算出各细节结构块的c值,若都小于等于阈值μ2,属于纹理结构,反之属于边缘结构。
步骤3,融合。平滑结构采用算术加权融合算法;边缘结构和纹理结构分别训练出各自的K-SVD字典,采用稀疏表示算法进行融合,融合规则为系数稀疏度和l1范数组合取大的原则,并且将边缘结构稀疏表示的残余量进行小波变换融合后,再加到边缘融合图像中。
步骤4,重构。3种模型的融合图像相结合,再除以每个位置像素值叠加的次数,最终获得融合结果图像F。
3 实验结果及分析
本文实验采用的4组图像如图3所示,分别取大小为256×256的多聚焦图像、医学图像和红外图像。待融合图像图3a、图3e和图3b、图3f表示左清晰和右清晰的多聚焦图像;图3c、图3g表示可见光图像和红外图像;图3d、图3h表示不同模态的CT和MRI医学图像。实验将本文算法分别与小波变换法(DWT)、Contourlet变换法、稀疏表示法(SR)进行对比。实验用MATLAB R2012a编程,在2 Gbyte内存的Windows7系统上实现。

图3 源图像
本文算法需对源图像进行块分类。文献[4]指出随着图像分块的增大,融合图像的全局误差会减少,因此4×4和 6×6 分块会影响图像全局信息使得融合指标降低。而16×16分块过大不仅字典维数变大运算复杂量变大,且不利于子块局部特征的分割,融合效果不佳。8×8分块相对保存更多的图像信息,融合效果更好。综上所述,本文算法选择8×8分块。
在实验中,本文算法取μ1=13,μ2=0.75。SR采取8×8分块,选择K-SVD字典,融合规则为系数稀疏度和l1范数组合取大原则。Contourlet变换法采用5层分解,融合规则为低频系数采用算术平均,高频系数采用绝对值取大。DWT的融合规则为低频系数选用加权平均,高频系数选用绝对值取大进行融合。实验结果如图4所示。

图4 融合实验结果图
从主观上评价融合结果图像,图4a和图4b中明显其字母和数字都比较模糊,说明DWT的多聚焦融合图像会缺失图像信息;图4c对比度低,很难分辨红外图像中有效信息;图4d的医学融合图像也出现了对比度低和不清晰的现象。图4e和图4f在字母和闹钟的边缘出现了严重的虚影现象,这些虚影是Contourlet变换法在分解图像中进行下采样引起的;SR和本文方法的融合图像在清晰度和对比度上都明显优于前两种方法。为了更好评价两者,对SR和本文方法的融合图像中矩形框的内容进行放大,如图5所示。

图5 融合结果的局部放大图
从局部放大图可以看出图5e和图5f中字母和数字比图5a和图5b更加清晰。在图5c中左上角的轮胎明显没有图5g清晰,并且在融合图4k中图像下部分有出现“雾气”现象,融合效果不佳。图5h相对5d有更良好的内脏纹理信息。由此说明本文方法相对SR保存了更多图像信息,融合效果更好。
实验结果分析采用主观评价和客观评价,客观评价包括了相关系数(MI)、空间频率(SF)、平均梯度(AG)[10]的指标。其中MI越大,说明结果图与源图像相关性越大,而SF和AG指标值越高,说明图像越清晰,包含的图像信息越多。
表1给出了4组融合结果图像的客观指标。从表1的Pepsi实验数据中,SR和本文算法的指标均明显超越了DWT和CT,融合的质量有改善,本文算法比SR的性能指标又有显著提高。在Clock实验数据中,可以看出CT的融合效果最差,DWT和SR的性能指标稍好,本文算法的性能相比于传统方法有明显改进。而Gun和Med的实验数据中,SR和本文方法的指标具有压倒性的优势,本文算法相对SR性能指标有所提高。由此可见,本文算法的融合效果很理想。
表1 评价指标的比较

客观指标图像DWTCTSR本文算法MIPepsi70886622567379076862Clock70447608737365474907Gun15014116671788525043Med30365145333911539682SFPepsi138220140968167592191302Clock143423105948141834145656Gun4642146648186512212281Med7871399561163120172327AGPepsi51910577626101469847Clock59991435235877260324Gun266932555797649117726Med29348383376563068527
表2给出了传统稀疏算法和本文算法在同样实验环境下分别对图2中4组图像进行融合的执行时间比较。实验中本文算法和SR都采取8×8的滑动分块方式,选择K-SVD字典和OMP进行稀疏编码,并选用相同的融合规则。Pepsi实验中,稀疏算法运行时间为1 260 s,本文算法运行时间为928 s。在2个多聚焦图像实验中,本文算法相对传统稀疏算法均缩短了近1/4的时间;Clock实验中,稀疏算法耗费了 1 288 s, 本文算法耗费985 s。在红外图像Gun实验中,稀疏算法运行 1 041 s, 本文算法的时间缩短了近3/5。在医学图像Med实验中,稀疏算法耗费716 s,本文算法缩短了近1/4的时间。由此可见,本文算法确实有效地加快了融合速度。
表2 实验时间数据
s

算法PepsiClockGunMedSR126005712882441041266716321本文算法928881985393415174544841
4 结束语
本文提出了一种基于块分类稀疏表示的图像融合算法,根据图像局部特性将其分为平滑结构和细节结构,并将细节再划分为方向一致性强的边缘结构和方向不规则的纹理结构。其平滑结构采用算术平均融合算法,边缘和纹理结构采用多字典的稀疏表示融合算法,并对边缘结构稀疏表示中的残余量采用小波变换融合算法。实验结果表明,该算法的融合效果有显著改善,并且算法速度也有提高,使得图像融合技术能够在军事、工业、交通等领域中得到更好的实际应用。
[1] WANG W, CHANG F, JI T. Fusion of multi-focus images based on the 2-generation curvelet transform[J]. International Journal of Digital Content Technology and Its Applications, 2011, 5(1):33-42.
[2] BIN Yang, LI Shutao. Multifocus image fusion and restoration with sparse representation[J]. IEEE Trans. Instrumentation and Measurement,2010, 59(4):884-892.
[3] 陈垚佳,张永平,田建艳.基于分块过完备稀疏表示的多聚焦图像融合[J].电视技术,2012,36(13):48-51.
[4] 余南南,邱天爽.稀疏表示的自适应遥感图像融合算法[J].信号处理,2013,29(6):663-667.
[5] BIN Yang,LI Shutao. Pixel-level image fusion with simulta- neous orthogonal matching pursuit[J]. Information Fusion, 2012,13(1):10-19.
[6] LI Shutao,YIN Haitao,FANG Leyuan. Remote sensing image fusion via sparse representations over learned dictionaries[J]. IEEE Trans. Geoscience and Remote Sensing, 2013, 51(9): 4779-4789.
[7] JIANG C, ZHANG H, SHEN H, et al. Two-step sparse coding for the pan-sharpening of remote sensing images[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(5):1792-1805.
[8] 练秋生,张伟.基于图像块分类稀疏表示的超分辨率重构算法[J].电子学报,2012,40(5):920-925.
[9] 翟雪含,朱卫平,康彬.结合KSVD和分类稀疏表示的图像压缩感知[J].计算机工程与应用,2015(6):193-198.
[10]QU G, ZHANG D, YAN P. Information measure for performance of image fusion[J]. Electronics Letters, 2002, 38(7): 313-315.
陈利霞(1979— ),女,博士,副教授,研究方向为数字图像处理、小波、偏微分方程及应用;
李 子(1990— ),女,硕士生,研究方向为图像融合、稀疏表示;
袁 华(1975— ),硕士,讲师,研究方向为图像处理、智能信号处理,本文通讯作者;
欧阳宁(1972— ),硕士,教授,研究领域包括智能图像处理、智能信息处理、数据融合、计算机应用等。
责任编辑:时 雯
Image Fusion Algorithms Based on Sparse Representation of Classified Image Patches
CHEN Lixiaa,b,c,LI Zid,YUAN Huad,OUYANG Ningd
(a.GuangxiCollegesandUniversitiesKeyLaboratoryofIntelligentProcessingofComputerImagesandGraphics;b.SchoolofMathematicsandComputingScience;c.GuangxiKeyLaboratoryofCryptographyandInformationSecurity;d.SchoolofInformationandCommunication,GuilinUniversityofElectronicTechnology,GuangxiGuilin541004,China)
To solve the problem of the fusion algorithm based on sparse representation ignores the local characteristics of the image, an algorithm based on sparse representation of classified image patches is proposed in this paper. In this method, image patches are divided into the smooth, the edge and the texture categories according to local features of the image. The edge and texture structure patches are applied into training the corresponding redundant dictionary. During the fusion process, arithmetic average approach is used for smooth structure patches while edge and texture structure patches are fused by sparse representation algorithm using their corresponding dictionary, and the residual images of the sparse edge structure are fused by a wavelet fusion method. Experiment results show that the proposed algorithm significantly improves the subjective performance and objective performance indexes of fused image and has faster speed than other single dictionary methods.
patch classification;sparse representation; image fusion
国家自然科学基金项目(61362021);广西自然科学基金项目(2013GXNSFDA019030;2013GXNSFAA019331;2012GXNSFBA053014;2012GXNSFAA053231;2014GXNSFDA118035);广西科技开发项目(桂科攻1348020-6;桂科能1298025-7);广西教育厅项目(201202ZD044;2013YB091);广西高校图像图形智能处理重点实验室资助项目(GIIP201408);桂林市科技攻关项目(20130105-6;20140103-5);桂林电子科技大学研究生教育创新计划资助项目(GDYCSZ201462)
TN911.73
A
10.16280/j.videoe.2015.17.005
2014-12-25
【本文献信息】陈利霞,李子,袁华,等.基于块分类稀疏表示的图像融合算法[J].电视技术,2015,39(17).
验结果证明,该算法相对于单一字典稀疏表示算法,在融合图像的主观评价和客观评价指标上都有显著改进,并且算法速度也有提高。

