脉冲喷动微波真空干燥器内喷动流化动力特性的数值研究

李 静,金光远,2，*,张 慜,2,崔政伟,仲建勋

(1.江南大学食品先进制造装备技术江苏省重点实验室,江苏无锡 214122;2.江南大学食品科学与技术国家重点实验室,江苏无锡 214122)

脉冲喷动微波真空干燥器内喷动流化动力特性的数值研究

李 静1,金光远1,2，*,张 慜1,2,崔政伟1,仲建勋1

(1.江南大学食品先进制造装备技术江苏省重点实验室,江苏无锡 214122;2.江南大学食品科学与技术国家重点实验室,江苏无锡 214122)

为探索脉冲喷动微波真空干燥系统(PSMVD)中气固喷动流化床的动力特性,采用基于无粘性两相流理论,使用计算流体力学欧拉-欧拉方法(CFD)对二维喷动流化床中喷动流化特性进行了数值研究,对喷动流化床的动力特性和颗粒运动分布特征进行了揭示,这些因素影响颗粒空间位置分布和其微波加热的均匀性。结果表明,采用欧拉-欧拉双流体模型,成功获得脉冲喷动微波真空干燥腔内的二维喷动流化床的喷动流化动力特性;喷动流化过程在特定气流喷动速度下有一个初始阶段和准稳态流化阶段;喷动速度是控制颗粒在喷动床中颗粒位置的重要因素,存在一个影响流化模式转变的关键喷动速度;射流穿透深度和喷射速度之间存在线性关系。

真空微波干燥器,喷动流化床,气固两相流,数值模拟

近年来,微波真空干燥(MVD)作为一种潜在的获得优质食品产品的干燥方法在食品工业进行了初步的应用,包括干果制品、蔬菜、谷物[1-2]。目前由于干燥腔内电磁场的空间分布不均匀导致温度场分布不均匀,产品出现冷热斑点,这个问题阻碍了这一技术的广泛应用。同时微波干燥不均匀的温度分布也产生了食品微生物安全问题[3-4]。微波真空干燥加热均匀性受多种因素影响,例如真空腔结构、物料空间位置、微波干燥腔内的空间电磁场强度[1,5]。一些研究显示,微波能量均布可以通过电磁场平均技术、机械运动方式或者气动搅拌来获得[6-8]。

流态化过程为干燥床中的颗粒提供了一种气体搅拌。由于颗粒表面不断生成的新边界层,有利于传热传质的进行[9-10]。由于粗糙的食物颗粒如切块或切片材料,尤其是当其水分含量较高,表面较粘时难以通过传统的流化床流化,脉冲喷动床可用于流化颗粒较粗,应用于微波真空干燥被认为是解决加热不均匀的问题的一种有效手段。虽然一些研究人员已经采用脉冲喷动微波真空干燥(PSMVD)这个新技术对食品物料的干燥特性进行实验研究[11-13],对于流化机理仍需要进一步理论研究,以了解在脉冲喷动微波真空干燥技术的干燥机理。

计算流体力学(CFD)方法被认为是一个有效的工具,以获得复杂的气固两相流的流体动力学特性[14]。两种不同的方法常用于模拟流化床或喷动床的两相流动,即欧拉-欧拉(EE)和欧拉-拉格朗日(EL)方法[15-17]。在本研究中,对于在脉动喷动微波干燥系统中简化二维喷动流化床的喷动流化过程,采用欧拉-欧拉双流体模型方法进行探究。对流化喷动床的动力特性和不同喷动气流速度下颗粒运动分布特征进行探索,有助于明确PSMVD系统干燥的控制因素,改善颗粒空间微波加热的均匀性。

1 材料与方法

1.1 材料与仪器

以来自中国宁波海通集团农场里的新鲜莴苣作为研究对象。莴苣洗净去皮,测量获得莴苣的物理属性,采用FA1104电子天平测量质量,采用E5061矢量网络分析仪测量介电特性,水分含量采用国标烘箱方法,所有测量过程进行三次,取平均值[12-13],本次研究中莴苣质量为200.0g。

图1 脉冲喷动微波真空干燥系统Fig.1 Schematic diagram of a laboratory pulsed spouted microwave-vacuum drying system注：1.进料阀,2.板阀,3.微波加热腔,4.微波发生器,5.循环水冷装置,6.干燥腔,7.和13压力表,8.气固分离器,9.气体浓缩器,10.真空泵,11.气流电磁阀,12.气流调节阀,14.气源,15.控制面板,16.水管,17.气体分布器,18.喷动管,19.硅橡胶塞,20.物料,21.干燥室,22.固定装置,23.光纤温度传感器。

实验室PSMVD实验设备有七个基本部分组成,其原理图如图1所示。干燥箱内的压力可以调节在3.5～100kPa的范围。包括:(1)圆柱多模微波腔,配有四个2450MHz微波发生器;(2)一个圆形管道真空干燥箱;(3)一个脉冲喷动系统,配备了一套可调气体流动和分配单元以及一套1cm3/min空气处理单元;(4)供热系统。每个磁控管的输出功率是在0.1到1.0kW由GPA-1.8kW微波功率控制器所控制;(5)水负载系统,被用来防止磁控管过热;(6)真空系统配有冷却器和水循环真空泵,泵输送率为1cm3/min。

1.2 实验方法

1.2.1 计算模型 本文采用欧拉-欧拉无粘性双流体理论研究真空压力条件下在喷动流化床中气固两相流的动力学特性。努森数是稀薄气体的一个无量纲参数。由于脉冲喷动微波真空干燥系统中,真空努森数(绝对压力,7000Pa)远远低于1,符合流体连续介质假设,可以由纳维尔斯托克斯方程(N-S方程)求解真空流动[18]。在CFD(ANSYS FLUENT 13.0,America)软件中对PSMVD设备中的气固两相流模拟。其中莴苣颗粒假设为球形,直径为5mm。

在目前的二维流化床(2D喷动床),喷动流动被简化为一个二维流,如图2所示。干燥室的宽度是40.0mm,腔高度H为 516.0mm;空气分布喷口的宽度L是8.0mm,空气分配器角度是45°。空气和莴苣颗粒分别被看做气相和颗粒相。

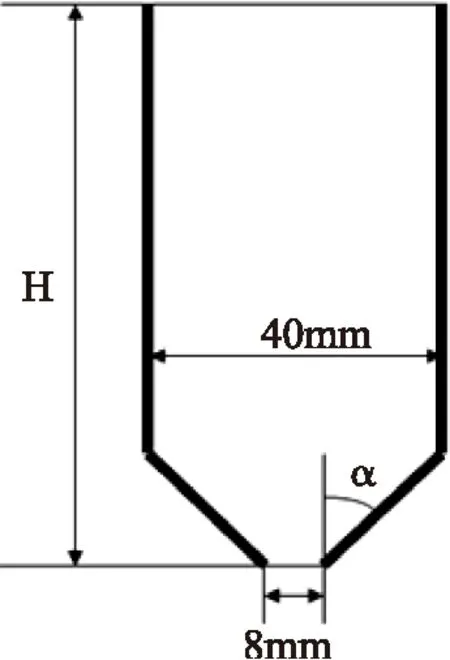
图2 二维喷动流化床计算模型Fig.2 Computational models of air distribution structure

1.2.2 数值方法 气固两相流场采用ANSYS FLUENT求解器,通过求解雷诺数平均值的N-S方程来计算获得。采用体积分数的隐式方案,层流粘性模型,压力速度耦合SIMPLEC算法,最小二乘法为基础的一阶迎风空间离散,和一阶隐式瞬态格式。喷射空气和莴苣颗粒分别被设置为主相和次相。空气和颗粒之间的相互作用被认为是颗粒流动的阻力和碰撞。采用结构网格策略,利用ANSYS ICEM进行网格剖分。网格包含370000个单元,单元的最小尺寸为0.01mm。进行网格无关性计算,保证当前网格尺寸的计算结果不依赖于网格疏密。

本文模拟边界条件定义如下:入口被指定为速度入口,并且指定为主相速度;出口被指定为压力出口,重力和颗粒体积分数被指定。瞬时时间步长设置0.001秒。为了考察喷动速度对流化特征的影响,选用若干气流喷动速度工况进行模拟(气流喷动速度 uspout=3.5、7、14、28、56m/s)。

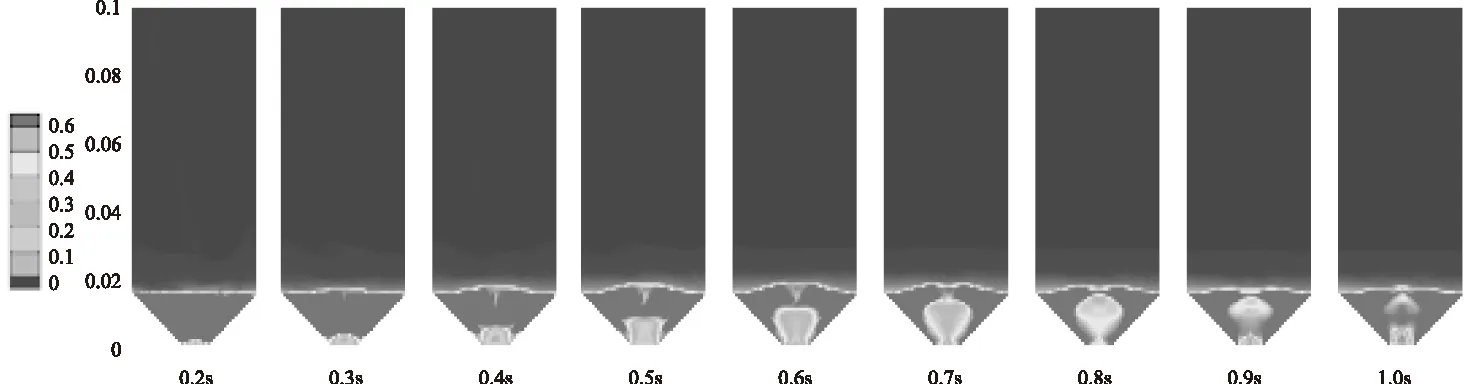
图3 最小喷动流化速度下颗粒体积分布Fig.3 Particle volume fraction at the minimum spout fluidization velocity注:uspout=3.5m/s,t=0.2～1.0s。

2 结果与讨论

2.1 最小流化速度下喷动流化特征

当前欧拉模型下莴苣颗粒发生流化时的最小流化速度为3.5m/s,其颗粒相体积分数和速度如图3和图4所示。由图3和图4可以看出,莴苣颗粒在气流喷动1.0s后保持传统的固定床状态。在喷动流化床整体流态化过程包括初始阶段和稳定阶段。初始阶段是射流穿透床层的一个瞬态发展过程,其中,所述射流最初出现,然后无干扰的周期性地分裂成气泡的第二阶段,是一个稳定的循环过程,其中颗粒循环在一个固定的模式。在离喷射入口高度为29.0mm处形成悬浮颗粒界面,大多数颗粒占据空气分布器底部,很少的颗粒能够逃离这个界面,此时最大颗粒速度达0.1m/s。

图4 最小喷动流化速度下颗粒速度分布 Fig.4 Particle velocity at the minimum spout fluidization velocity注:m/s,uspout=3.5m/s,t=1.0～3.0s。

2.2 流动稳定性

随着喷口处气体流速的增加,喷动流化床的气固两相流体动力学特性开始改变。微波干燥腔内两相流动稳定性如图5所示,给出了在不同气体喷动速度下,位于初始静止时颗粒表面中间点处的静压力脉动特征和莴苣颗粒的速度脉动特征;整个喷动流化有一个明确的约1.0秒的不稳定初始过程,在这种初始波动阶段后,当气体喷射速度不高于21m/s时趋于稳定。 随喷动速度增加,这种不稳定状态的持续时间增加,且静压值趋于降低,而静压波动幅值趋于增大。在相同位置莴苣颗粒速度如图6所示,颗粒速度在初始阶段差异较大,当喷动速度不高于21m/s时稳定。 当喷动速度达到28m/s,颗粒速度显著增加,特点是周期性波动,并且表现为振动的流态化。上述分析表明,喷动速度是影响喷动流化特征的一个重要因素,存在一个关键喷动速度影响喷动流化模式转变;整个流化过程可分为两个阶段:初始阶段和准稳态流化阶段。

图5 不同喷动速度下干燥腔内静压脉动Fig.5 Fluctuation of static pressure at different spout gas velocity

图6 不同喷动速度下干燥腔内粒子脉动特征Fig.6 Fluctuation of particle velocity at different spout gas velocity

2.3 颗粒流的发展过程

当喷口气体速度达28m/s,考虑到颗粒流的波动特性,分别讨论在喷动流速为14m/s和28m/s的情形来明确影响流动模式转变的关键喷动速度。

图7 粒子体积分数分布Fig.7 Particle volume fraction注:uspout=14m/s,t=0.1～1.0s。

图9 粒子体积分数分布Fig.9 Particle volume fraction distribution注:uspout=28m/s,t=0.1～1.0s。

图7和图8显示了喷动速度为14m/s,喷动时间为0.1～3.0s内的瞬时颗粒流动特征,颗粒流动初始阶段t=0.1～1.0s秒的粒子分布情况,如图7所示,进入准稳态流化阶段,粒子运动特征如图8所示。与喷动速度3.5m/s相比,初始阶段射流产生了更多、更大的气泡,导致该区域更频繁的颗粒运动。随着射流发展,大多数颗粒在喷动气流携带作用下获得提升,并形成一个球形分布区域。但仍有一小部分颗粒分布在空气分配器壁的附近,颗粒积聚发生在空气分配器底部。喷动时间间隔0.5s从1.0s到3.0s,颗粒速度和最大提升高度分布结果如图8。当颗粒流动模式处于一个稳定的状态,在高度45mm喷口上方形成颗粒悬浮界面。最高的颗粒速度位于球形分布区域,这表明在此工况下喷动流化床有两条颗粒循环轨迹。少数颗粒从悬浮表面逸出,颗粒速度的最大值达0.3m/s(标尺未给出)。

如图9和图10所示是喷动速度在28m/s的瞬时颗粒流动模式。瞬时流动模式在1.0s的初始阶段时,带有更多更大气泡的射流迅速出现,穿透颗粒床层,并与大多数颗粒显著升高了。随喷动射流发展,积累在空气分配器器壁的颗粒被携带到上部区域。在这种情况下,喷动射流引起大多数颗粒在横向和轴向方向的运动。颗粒悬浮高度位于喷口上方150到250mm,颗粒流动具有一定的波动特征,喷口处颗粒流动是不稳定的(图10)。 与喷动速度为14m/s的颗粒流相比,颗粒速度的最大值增大至1.6m/s(标尺未给出),更高速度颗粒的分布位置移至20～100mm高度区域。存在一个含有较低速度颗粒的狭窄区域,这可能是由主喷口气体流动引起的。

在不同的喷口速度流动模式的特征表明,喷动气流速度和颗粒状态密切相关,存在一个关键喷动速度,影响颗粒流动模式的转变。

图8 随喷动时间发展的粒子速度分布(uspout=14m/s)Fig.8 Particle velocity distribution at different spout time(uspout=14m/s)

图10 随喷动时间发展的速度分布(uspout=28m/s)Fig.10 Particle velocity distribution at different spout time(uspout=28m/s)

2.4 喷射气流的穿透特性

在喷动流化床中,无论气体以气泡的形式离开喷口,还是以脉动喷射或连续喷射的形式离开,喷射区域存在大量的气体和固体混合[19]。射流穿透深度来表征喷口气流的关键参数,它也随着喷动流化床中喷射气体的速度提高而提高。用来预测射流穿透深度的不同模型之间的差异主要是由于射流边界的不同定义[20]。在本文中,射流穿透深度定义为孔隙率为0.8的等值线[21]。喷动气体速度对穿透深度和压力降影响如图11所示。在低于28m/s的喷动气流速度下穿透深度增加缓慢,直到56m/s才迅速增加。在射流穿透深度和气体喷动速度之间存在一个近似线性关系。

床层压降是表征真空流化床干燥器颗粒循环模式的另一个重要的参数,在准稳态阶段,定义气固混合物进口和出口之间压差为压降(ΔP)。图11所示床压降表明,当管口的气体速度从14m/s增加到21m/s,该压降从负压变为正压。这种现象表明粒颗粒循环模式的一个重要变化,喷口的气流作用于颗粒的提升力克服了颗粒的重力,颗粒开始被从空气分配器底部提升到真空腔室的上部区域。因此,从14m/s至28m/s的速度范围是一个影响颗粒循环模式的关键喷动速度区域。

图11 喷动流化穿透深度和压降Fig.11 Penetration depth and Pressure drop for a 2D vacuum cavity

3 结论

本文成功采用欧拉-欧拉双流体模型,获得脉冲喷动微波真空干燥腔内的二维喷动流化床的喷动流化动力特性。基于模拟结果,分析喷动流化床的动态特性和在不同喷动速度工况下喷动气流对颗粒运动模型的影响规律。在一定喷动速度下,流化过程可分为两个阶段:初始阶段和准稳态流化阶段。喷口速度是控制颗粒在喷动流化床中位置的重要因素。存在一个关键喷动速度区间,在此范围内,颗粒流动模式由稳态转化为非稳态流动。射流穿透深度与气体喷动速度之间存在一个近似的线性关系。在准稳态阶段,随着喷口速度增加颗粒循环模式明显改变,粒子开始被提升到真空干燥器上部区域。

[1]Zhang M,Jiang H,Lim RX. Recent developments in microwave-assisted drying of vegetables,fruits,and aquatic products-Drying kinetics and quality considerations[J]. Drying Technology,2010,28(11):1307-1316.

[2]Li ZY,Wang RF,Kudra T. Uniformity issue in microwave drying[J]. Drying Technology,2011,29(6):652-660.

[3]Vadivambal R,Jayas DS. Non-uniform temperature distribution during microwave heating of food materials-A review[J]. Food and Bioprocess Technology,2010,3:161-171.

[4]Jangam SV. An overview of recent developments and some R&D challenges related to drying of foods[J]. Drying Technology,2011,29(12):1343-1357.

[5]Zhang M,Tang J,Mujumdar AS,et al. Trends in microwave-related drying of fruits and vegetables[J]. Trends in Food Science & Technology,2006,17(10):524-534.

[6]Torringa HM,Dijk EJV,Bartels PV. Microwave puffing of vegetables:modeling and measurements[J]. In:Proceedings of 31st microwave power symposium,1996,16-19.

[7]Balakrishnan M,Raghavan GSV,Sreenarayanan VV,et al. Batch drying kinetics of cardamom in a two-dimensional spouted bed[J]. Drying Technology,2011,29(11):1283-1290.

[8]Feng H,Tang J. Microwave finish drying of diced apples in a spouted bed[J]. Journal of Food Science,1998:63(4),679-683.

[9]Feng H,Tang J,Cavalieri RP,Plumb OA. Heat and mass transport in microwave drying of porous materials in a spouted bed[J]. AIChE Journal,2001,47(7):1499-1512.

[10]Jambhale AS,Barbadekar BV. Microwave drying system with high-tech phase controller:a modified applicator[J]. World Acad Sci Eng Technol,2008,46:1-5.

[11]Wang Y,Zhang M,Mujumdar AS,et al. Study of drying uniformity in pulse-spouted microwave-vacuum drying of stem lettuce slices with regard to product quality[J]. Drying Technology,2013,31(1):91-101.

[12]Wang Y,Zhang M,Mujumdar AS,et al. Microwave-assisted pulse-spouted bed freeze-drying of stem lettuce slices-effect on product quality[J]. Food and Bioprocess Tech. 2013,6:3530-3543.

[13]Wang Y,Zhang M,Mujumdar AS,et al. Experimental investigation and mechanism analysis on microwave freeze drying of stem lettuce cubes in a circular conduit[J]. Drying Technology,2012,30(11-12):1377-1386.

[14]Rahimi M R,Azizi N,Hosseini SH,et al. CFD study of hydrodynamics behavior of a vibrating fluidized bedusing kinetic-frictional stress model of granular flow[J]. Korean Journal of Chem. Eng.,2013,30(3):761-770.

[15]Pai M,Subramaniam SA. Comprehensive probability density function formalism for multiphase flows[J]. Journal of Fluid Mechanics,2009,628:181-228.

[16]Bouillard J,Lyczkowski R,Gidaspow D. Porosity distributions in a fluidized bed with an immersed obstacle[J]. AIChE Journal,1989,35:908-922.

[17]Pritchett J,Blake T,Garg S. A numerical model of gas fluidized beds[C]. AIChE Symp.,1978,176:134-148.

[18]Shen C. Rarefied gas dynamics:fundamentals,simulations and micro flows[B]. Publisher:Springer-Verlag Berlin and Heidelberg GmbH & Co. K. 2005.

[19]Hong R,Guo Q,Luo G,et al. On the jet penetration height in fluidized beds with two vertical jets[J]. Powder Technology,2003,133(1):216-227.

[20]Musmarra D. Influence of particle size and density on the jet penetration length in gas fluidized beds[J]. Industrial & Engineering Chemistry Research,2000,39(7):2612-2617.

[21]Gidaspow D,Ettehadleh B. Fluidization in two-dimensional beds with a jet hydrodynamic modeling[J]. Industrial & Engineering Chemistry Fundamentals,1983,22(2):193-201.

Numerical study on spout fluidization dynamics in pulsed-spout microwave-vacuum dryer

LI Jing1,JIN Guang-yuan1,2，*,ZHANG Min1,2,CUI Zheng-wei1,ZHONG Jian-xun1

(1.Jiangsu Province Key Laboratory of Advanced Food Manufacturing Equipment and Technology,Jiangnan University,Wuxi 214122,China;2. China State Key Laboratory of Food Science and Technology,Jiangnan University,Wuxi 214122,China)

The dynamic characteristics of gas-particle spout fluidized bed in a microwave-vacuum drying system(PSMVD)were investigated. The spout fluidization process in a Pseudo-2-D spouting bed was monitored by computational fluid dynamics(CFD)using the inviscid Two-fluid theory based on Euler-Euler method. The dynamic characteristics of the spout fluidized bed and the effect of spout elevation on the particle movement were revealed,which could be used to improve the uniformity of particle mixing and microwave heating. The results revealed that mathematical model succeeded to demonstrate the dynamic characteristics of gas-particle spout fluidized bed in a microwave-vacuum drying system;the spout fluidization process includes isolated,merged and transitional jets and the fluidization at specific spout gas velocity had a start-up stage and a quasi-steady fluidization stage. The spout velocity was an important factor controlling particle status in the spout fluidized bed and a critical velocity was identified for effect transition of the flow pattern. There was an approximately linear correlation between the jet penetration depth and the spout velocity.

microwave-vacuum dryer;spout fluidized bed;two phase flow;numerical simulation

2014-05-05

李静(1972-),硕士,讲师,主要从事食品加工装备和无损检测问题研究。

*通讯作者:金光远(1979-)，女，博士，讲师，研究方向：食品加工装备。

江苏省博士后基金项目,江苏省青年基金项目(BK20130150)。

TS255-35

A

1002-0306(2015)11-0079-05

10.13386/j.issn1002-0306.2015.11.008