带有高阶滑模微分器的制导控制一体化设计*
周觐,雷虎民,李炯,邵雷
(空军工程大学 防空反导学院,陕西 西安 710051)
带有高阶滑模微分器的制导控制一体化设计*
周觐,雷虎民,李炯,邵雷
(空军工程大学 防空反导学院,陕西 西安 710051)
针对制导控制一体化模型中由于目标机动加速度难以测量的问题,提出了应用高阶滑模微分器,对导弹导引头获得的弹目相对运动信息进行微分,从而解算出目标加速度的方法。在最后开展了导弹六自由度仿真验证,将高阶滑模微分器得到的目标加速度与真实值进行对比,验证了方法的有效性。
制导控制一体化;高阶滑模微分器;滑模控制;反演控制
0 引言
高超声速飞行器技术的蓬勃发展对我国防空反导体系构成了巨大挑战,传统的防空导弹制导与控制性能已经难以抵抗现代战争中高超声速飞行器所带来的威胁,正因如此,制导控制一体化技术应运而生。与传统的制导与控制系统分开设计不同,制导控制一体化技术将导弹制导回路与控制回路整合为一个回路,即根据导弹目标的相对运动关系直接得到控制指令,省去了中间的指令过载与控制指令之间的转换环节,从而能够有效提高武器制导控制精度,减小脱靶量[1~5]。
Tal Shima等[4]以基于零控零化脱靶量思想建立了导弹俯仰平面制导控制一体化模型,应用滑模控制方法对模型进行了控制,仿真结果表明制导控制一体化设计相比于传统分回路设计能够取得更高的制导精度。段广仁等[5]以零化视线角速率为目标,利用非线性状态变换将导弹俯仰通道制导控制一体化模型转换为标准形式,基于滑模思想设计了滑模控制算法。仿真结果表明,在目标机动情况下,该模型相对于传统分回路设计能够取得更小的脱靶量。侯明哲等[6]在文献[5]的基础上建立了具有严格反馈形式的导弹目标三维相对运动状态模型,应用滑模反演控制方法设计了制导控制一体化算法。六自由度仿真结果表明,在加入目标机动以及导弹自身的不确定性条件下,所设计算法能够获得更好的制导精度以及更小的控制能量。Alexander[7]等针对目标信息难以获得的情况,在制导控制一体化算法中加入了高阶滑模微分器对目标状态进行估计,并通过仿真将改进后制导控制一体化算法与传统制导控制分开设计算法进行对比,验证了所设计方法的有效性。董飞垚等[8]应用最优滑模控制理论设计导弹制导控制一体化算法,张保群等[9]设计了导弹俯仰通道制导控制一体化模型,应用滑模自适应反演控制方法对模型进行了控制,仿真结果表明在目标机动和导弹参数摄动情况下,制导控制一体化模型能够取得更好的制导效果。
对于由于目标机动引起的不确定性以及制导控制所需的目标信息无法有效获得的问题,现有文献中大多采用设定不确定性上界的方法,但是对于不同的目标,其不确定性上界会有很大差异,如何有效设定以及估计不确定性的问题不能够很好解决。本文以此为出发点,应用高阶滑模微分器对目标的加速度信息进行估计,从而改进制导控制一体化算法,提高武器性能指标。
1 制导控制一体化模型建立
根据文献[6],在三维空间中的导弹和目标相对运动关系可以表示为
(1)

(2)
导弹自动驾驶仪的状态方程可以表示为[9]
(3)
式中:x1=(γ,β,α)T;x2=(ωx,ωy,ωz)T;u=(δx,δy,δz)T;

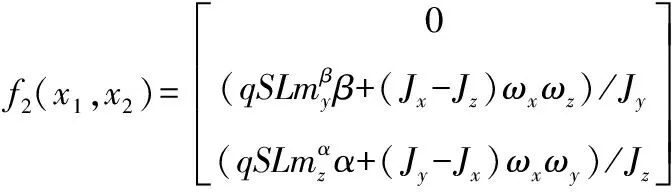
式中:α,β,γ,ϑ分别为导弹攻角,侧滑角,滚转角和俯仰角;q为动压;S为参考面积;vM为导弹速度。
导弹的加速度分量可以表示为[10]
(4)
(5)
式中:
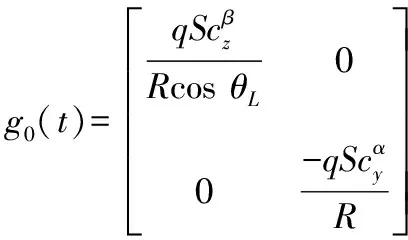
将式(3)和(5)合并,可以得到三维空间的导弹制导控制一体化模型:
(6)
2 高阶滑模微分器
从式(6)中可以看出,制导控制一体化算法的求取需要知道目标信息,即目标加速度在视线坐标系下沿Oy轴与Oz轴的分量。传统的方法是给定目标加速度的上界,应用滑模控制理论求解控制算法,但是对于不同的目标,其加速度上界的确定具有很大不同,而且应用在线估计逼近的方法对于算法的快速性又提出了更高的要求。对此,本文提出应用高阶滑模微分器的方法,利用导引头获取的弹目相对运动信息,对目标加速度进行准确有效的估计。
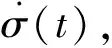
(7)
式中:第2项以及第3项称为非线性动态滑模面[10]。
SMD的Simulink模块图如图1所示。
待定参数ρ0,a,b需要满足以下条件:
(8)
定理1[11]:式(7)能够保证J0在有限时间内收敛到0,并且收敛误差一阶微分为

本文认为导弹装备了主动导引头,可以测量解算出导弹和目标之间沿视线各个轴向的加速度信息,以及视线仰角θL和视线偏角ψL。导弹和目标之间的相对速度可以表示为
(9)

图1 SMD结构图Fig.1 Simulink structure of SMD
式中:vT,vM分别为目标和导弹的速度;vrx,vry,vrz分别为视线Ox,Oy,Oz轴的相对速度;DCMTL,DCMML分别表示从目标速度坐标系到视线坐标系以及从导弹速度坐标系到视线坐标系之间的转换矩阵。将式(9)展开可以得到:
(10)
式中:θT,ψT为目标弹道仰角以及弹道偏角;vTxL,vTyL和vTzL分别为目标速度在视线坐标系下的分量。在末制导阶段,导弹和目标进入碰撞三角,认为导弹对准良好,针对迎击情况即有
cos(ψT-ψL)≈cos(-π)=-1,
则式(10)可以化简为
(11)
将式(11)进行微分可以得到:
(12)
则目标的加速度信息可以表示为
(13)
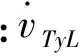
3 制导控制一体化算法设计
定义S0=x0-x0d,其中x0d为状态变量的目标值,在本文中x0d=0,对S0进行微分可以得到:
(14)

(15)
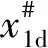
(16)

(17)
虚拟控制量可以选为
(18)
式中:k1为待设计参数。同样使x2d通过一个时间常数为τ2的低通滤波器。
(19)
最后定义S2=x2-x2c,对S2进行微分得到:
(20)
可以得到最后控制量为
(21)
式中:k2为待设计参数。

图2 SMD解算目标加速度Fig.2 Target maneuver estimation block
4 六自由度仿真验证
为了证明本文所提出的制导控制一体化算法的有效性,开展了导弹六自由度仿真验证,并且认为导弹滚转通道稳定不需要控制。
仿真过程中设计的目标的最大过载为15,有关导弹和目标初始状态参数以及初始弹目视线信息如表1所示。
仿真效果如图3~7所示。

表1 弹目初始参数及视线信息Table 1 Parameters of the missile, target and line-of-sight (LOS) initial condition
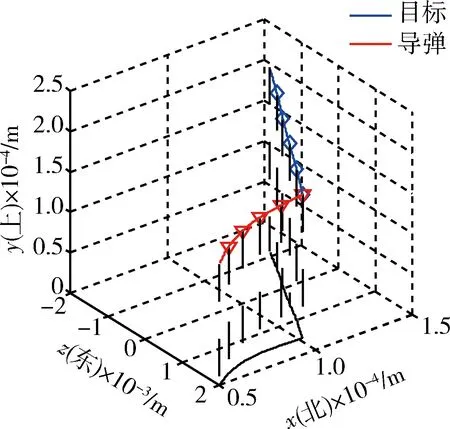
图3 弹目三维运动轨迹Fig.3 Trajectory of missile and target in three dimensional space

图4 弹目位置在分平面的投影Fig.4 Trajectory projection to the x, y and z axis

图5 SMD解算得到目标加速度与真实信息对比图Fig.5 Comparison of estimated target maneuver with its true information
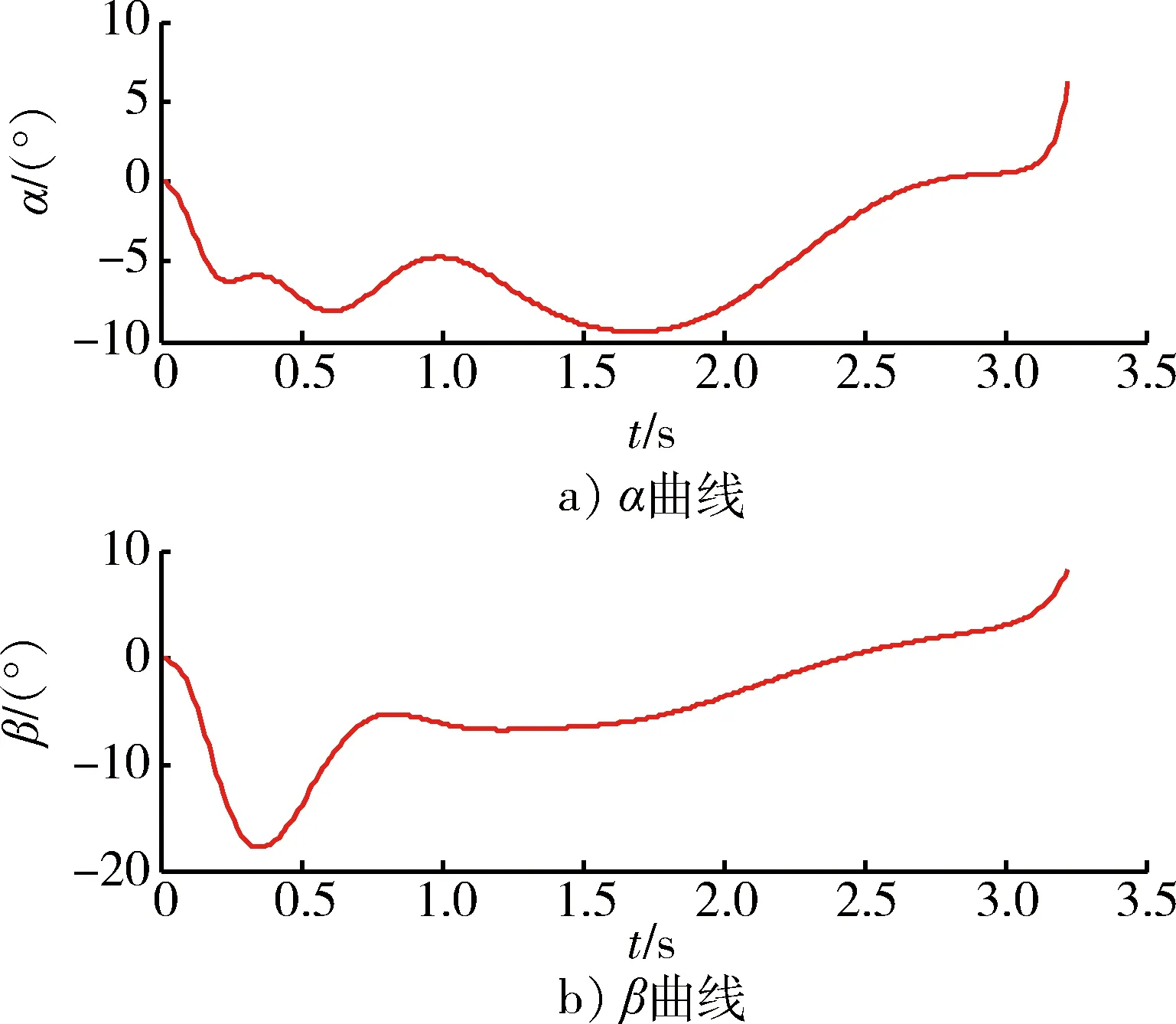
图6 导弹攻角α和侧滑角β变化曲线Fig.6 Curves of α and β
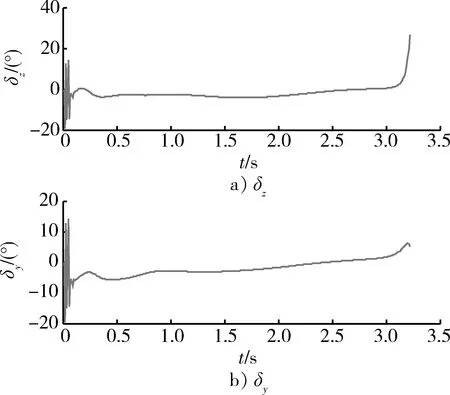
图7 导弹舵偏角δz和δy变化曲线Fig.7 Curves of fin deflection δz and δy
从图3和图4中可以看出,导弹轨迹平稳,最后准确命中目标,其脱靶量为0.463 94 m,达到了碰撞杀伤效果,有力提高了武器制导控制精度。从图5中可以看到,应用滑模微分器解算得到的目标加速度与目标真实加速度总体上吻合良好,经过大约0.1 s的调节时间后,SMD解算输出的目标加速度与真实值非常接近,并且在之后的时间内能够很好的跟踪目标加速度,验证了应用SMD对目标加速度进行估计的有效性和准确性。从图6和图7中可以看出,导弹姿态变化并不十分剧烈,舵偏角变化比较平稳,除了在开始大约0.1 s范围内有些抖震现象,这是由于在设定初始条件时导弹导引头视线角与真实视线角之间设定了5°的初始对准误差以及此时高阶滑模微分器的输出不稳定,可以看出算法能够快速消除误差角,而且在以后的变化过程中比较缓慢,有效验证了控制算法的快速性和鲁棒性。
5 结束语
本文针对制导控制一体化模型算法中目标机动信息难以获得的问题,引入了高阶滑模微分器,通过对导引头获得的弹目相对运动信息进行微分,解算出所需的目标加速度信息,从而对算法本身进行了完善提高,提升武器系统的制导控制精度,所研究方法具有一定的理论价值和工程参考价值。
[1] LIN C F, EVER J H. A LTV Dynamics Model for Missile Guidance and Control in the Endgame[C]∥AIAA
Guidance, Navigation, and Control Conference, Washington,1992:1024-1029.
[2] MENON P K, OHLMEYER E J. Integrated Design of Agile Missile Guidance and Autopilot Systems[J]. Control Engineering Practice,2001, 9(10):1095-1106.
[3] XIN M, BALAKRISHNAN S N, OHLMEYER E J. Integreted Guidance and Control of Missiles withθ-D Method[J]. IEEE Transactions on Control Systems Technology,2006, 14(6):981-982.
[4] SHIMAL T, IDAN M, GOLAN O M. Sliding-Mode Control for Integrated Missile Autopilot Guidance[J]. Journal of Guidance Control and Dynamics,2006, 29(2):250-260.
[5] 段广仁,侯明哲,谭峰.基于滑模方法的自适应一体化导引与控制律设计[J].兵工学报,2010,31(2),191-198. DUAN Guang-ren, HOU Ming-zhe, TAN Feng. Adaptive, Integrated Guidance and Control Law Design Using Sliding mode Approach [J]. Acta Armamentar, 2010, 31(2):191-198.
[6] HOU M Z, LIANG X L, DUAN G R, Adaptive Block Dynamic Surface Control for Integrated Missile Guidance and Autopilot[J]. Chinese Journal of Aeronautics,2013, 26(3):741-750.
[7] Alex Zhurbal, Moshe Idan. Effect of Estimation on the Performance of an Integrated Missile Guidance and Control System[J]. IEEE Transaction on Aerospace and Electronic Systems, 2011, 47(4):2690-2708.
[8] 董飞垚,雷虎民,李海宁,等. 一类带有加速度约束的非线性系统最优滑模控制[J].控制理论与应用,2012,29(10):1223-1226. DONG Fei-yao, LEI Hu-min, LI Hai-ning, et al. Optinal Sliding-Mode Control for Nonlinear Systems Subject to Acceleration Constraint[J].Control Theory and Application,2012,29(10):1223-1226.
[9] 张保群,宋申民. 基于自适应滑模控制的导弹制导与控制一体化反演设计[J]. 弹箭与制导学报,2009,29(5):31-35. ZHANG Bao-qun, SONG Shen-min. Integrated Playback Design of Missile Guidance and Control Based on Adaptive Sliding-Mode Control[J]. Journal of Projectiles , Rockets , Missiles and Guidance, 2009,29(5):31-35.
[10] Alex Zhurbal, Moshe Idan. Effect of Estimation on the Performance of an Integrated Missile Guidance and Control System[J]. IEEE Transaction on Aerospace and Electronic Systems, 2011, 47(4):2690-2708.
[11] KRUPP D R, SHKOLNIKOV I A,SHTESSEL Y B. 2-Sliding Mode Control for Nonlinear Plants with Parametric and Dynamic Uncertainties[C]∥AIAA Guidance, Navigation, and Control Conference and Exhibit,Denver, 2000:14-17.
[12] 焦晓红,关新民.非线性系统分析与设计[M],北京:电子工业出版社,2008. JIAO Xiao-hong, GUAN Xin-min.Analysys and Design of Nonlinear Systems[M].Beijing: Publishing House of Electronic Industry,2008.
Integrated Guidance and Control Design with Sliding Mode Differentiator
ZHOU Jin,LEI Hu-min,LI Jiong,SHAO Lei
(AFEU,Air and Missile Defense School, Shaanxi Xi’an 710051, China)
As the target information in the integrated guidance and control model are difficult to measure, a novel high order sliding mode differentiator (SMD) is introduced to get access to the target acceleration by differentiating the target and missile relative motion information obtained from the missile active homing seeker. The six degree of freedom simulation is carried out and a comparison between the estimated target maneuver information and its true data is made, which successfully verifies the effectiveness the proposed algorithm.
integrated guidance and control; high order sliding mode differentiator; sliding mode control; back-stepping control
2014-05-06;
2014-07-04
航空科学基金项目(20130196004)
周觐(1989-),男,河北衡水人。硕士生,研究方向为导航制导与控制。
通信地址:710051 陕西省西安市空军工程大学防空反导学院研2队 E-mail:zhoujindr@yahoo.com
10.3969/j.issn.1009-086x.2015.03.0014
TJ765
A
1009-086X(2015)-03-0077-06

