基于PID控制的数控机床进给伺服系统的建模与仿真
尚丽伟
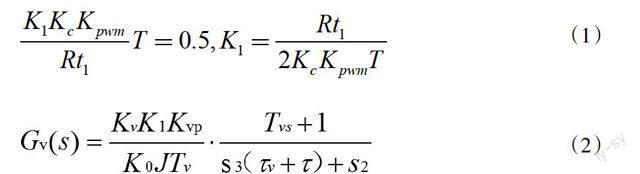
摘 要:进给伺服系统是数控装置与机床间的关键联接环节,是影响数控机床执行部件的加工精度、质量和加工效率的重要因素。文章在分析了数控机床进给伺服系统的基础上,建立了机床伺服系统的数字模型,通过仿真分析表明,PID控制器在机床操作过程中具有合理性。
关键词:数控机床进给伺服系统;PID控制器;建模
1 数控机床进给伺服闭环系统
数控机床进给系统分为伺服驱动系统和机械传动系统两部分。其中,伺服驱动系统与数控机床的精度、加工效率和稳定性等性能密切相关,是其关键组成部分。
数控机床进给伺服系统的主要作用是精确控制执行部件运动的位置、方向和速度,进给伺服系统的动、静态性能决定了数控机床的控制精度、稳定性和部件的加工效率。
2 数控机床进给伺服系统模型的建立
(1)伺服驱动装置的数学建模。交流永磁伺服电机(PMSM)是高精密数控机床进给伺服系统中常采用的伺服驱动装置,交流伺服电机须有矢量控制,相比较于直流永磁伺服电机,其噪音小、可靠性高。交流伺服电机由定子和转子两部分组成,其中转子是永磁铁,永磁铁在驱动器控制的U/V/W三相电形成的电磁场的作用下转动,伺服电机内的驱动器根据编码器的反馈信号与目标值比较,调整转子的转动角度。(2)机械传动装置的数学建模。数控机床进给系统接受数控系统发出的位置和速度指令,机床执行部件在工作台上根据设置参数进行切割加工,得到执行部件的位置作为系统输出。
机械传动系统的输入是伺服电机的角位移,输出是机床执行部件的位置。伺服电机与减速器相连接,通过联轴器与滚珠丝杠相连接,滚珠丝杠螺母副驱动执行部件作直线运动。
3 PID控制器的设计
(1)PID控制器的作用
PID控制是对整个控制系统进行偏差调节,最终达到执行部件的实际值与工艺要求的预期值相一致的目的。相比较与传统的机床进给系统控制,PID控制器具有算法简单、可靠性高、鲁棒性好的特点,在工业实际中被广泛应用。PID控制器由三部分组成,包括比例(P)、积分(I)和微分(D),线性控制器PID通过输入值与输出值之间的偏差值进行比例、积分和微分环节控制量输出,对机床执行部件进行控制。比例调节是成比例的反应控制系统的偏差,比例调节随着Kp的增大产生调节作用,由系统灵敏度和反应速度的增加,增大系统的调度量。但是若调度量过大,产生超调就会影响控制系统的稳定性。将差值信号进行事先放大,再结合实际情况进行调节可以有效避免这一矛盾。积分控制主要作用是消除系统的稳态误差,使系统的跟踪更精确。一旦系统产生误差,积分调节就会立即产生控制作用。积分调节的强弱与积分时间常数Ti成反比,积分时间常数Ti越大,积分控制的强度反而越弱,反之积分控制的强度就会越强。积分时间常数应选取适当,避免控制强度过大就会产生超调,影响系统的稳定。微分调节(Td)具有超前调节功能,当被控对象因系统扰动发生时间滞后,被控变量不能立即做出反应时,微分调节就会发挥作用,立即调节。微分调节与输入偏差的大小无关,只取决于输入偏差变化的速度。微分时间值越大,微分作用越强,反之微分作用越弱。微分调节不能单独使用,必须与比例调节和积分调节相结合,共同促进被控对象的控制质量。
(2)电流检测调节器。电流检测控制是交流进给伺服系统的重要组成部分,影响着整个伺服系统的精度和反映速度。伺服系统的电流控制部分宜采用模拟电路来实现,这有助于加快伺服系统的响应速度。电流控制的增益值是参数控制的关键,增加电流控制的增益有助于补偿电流在相位上的滞后效应增加控制的转矩。如果电流控制的增益过大,又会引起系统内部期间的漂移误差,影响转速的控制精度,造成电流控制的不稳定,同时,还会还会产生较大的磁场噪声和转矩脉动。电流控制内环的结构图如图4所示。
(3)速度检测调节器。速度控制亦是交流进给伺服系统的关键环节,其具有高精度、快响应的特点。交流伺服系统的速度控制器一般采用PI调节器。速度控制的增益比较复杂,受系统内部负载的影响,当负载的转动惯量与交流伺服电机的转动惯量的比值增加时,宜增加比例和积分的增益,保持控制系统的稳定;当负载的转动惯量与交流伺服电机的转动惯量的比值减少时,宜减小比例和积分的增益,以保证速度控制的精度和稳定性。
(4)位置检测调节器。
位置控制一般选用比例调节器。当位置控制增益增大时,连续位置跟踪的误差就会减小,但同时会影响到交流伺服系统的性能,也会较少伺服系统的稳定性。因此,一般设计前馈复合控制器来补偿系统的跟踪误差。
4 仿真分析
在建立了伺服系统数字模型的技术上,建立仿真模型,进行仿真分析。设定好系统的各项参数是仿真分析的关键。
加PID控制器的电流调节传递函数公式为:
(1)
(2)
设定参数:额定转矩为3000r/min,额定转矩为16.5N·m,转矩系数为1.51,额定电流为11.6A,电阻R为0.15Ω,SPWM系数为7.78,电动机轴转动惯量为0.01323kg·m2,电流调节反馈时间常数为100μs,速度调节的时间常数为0.01s,Kc为1。根据电流调节公式可求得校正参数:?子1=0.002s,K1=0.0794,根据速度调节公式求得校正参数:Tv=0.0527s,Kvp=0.499。位置调节的系数Kp由小到大通过MATLAB逐步进行仿真,直至将Kp减小到无超调。
仿真结果表明,采用PID控制器的速度调节环能够很好的对进给伺服系统进行控制,速度的超调量在10%以下。同时,增加了前馈控制模块的位置检测控制能够减小进给伺服系统的位置跟踪滞后问题,且效果显著。
5 结束语
数控机床进给伺服系统是一个比较复杂的系统,涉及到多种参数的设置。通过对数控机床进给伺服系统模型的建立和仿真分析表明,PID控制器可以增加进给伺服系统的鲁棒性、精确性和抗干扰能力,对我国数控机床技术水平、性能和质量的提高具有很重要的意义。
参考文献
[1]陈凡,范大鹏,张连超,等.数控测试用伺服进给系统非线性建模与仿真[J]. 组合机床与自动化加工技术,2010(4).
[2]王志刚.基于PMSM的伺服系统电流环的仿真[J].现代机械,2010(4).
[3]袁喻华,王莉.永磁同步电机矢量控制的MATLAB仿真研究[J].变频器世界,2010(4).
[4]杨林霖.数控机床伺服进给系统精度保持性试验研究[D].浙江大学,2014.
[5]李鹏杰.交流伺服进给系统的模糊PI控制仿真[D].华中科技大学,2013.

