Camassa-Holm方程的高阶局部中心间断Galerkin有限元法

马健军, 陈爱敏, 郝怡非(. 四川外国语大学 国别经济与国际商务研究中心, 重庆 40003; . 重庆大学 城市科技学院, 重庆4067)



Camassa-Holm方程的高阶局部中心间断Galerkin有限元法

马健军1, 陈爱敏2, 郝怡非1
(1. 四川外国语大学 国别经济与国际商务研究中心, 重庆 400031; 2. 重庆大学 城市科技学院, 重庆402167)

发展一个求解具有尖波解的Camassa-Holm方程的高阶局部中心间断Galerkin有限元法,该方法首先将Camassa-Holm方程改写为一个守恒律方程和一阶方程组的耦合系统,然后,使用局部中心间断Galerkin法求解该守恒律和使用有限元法求解一阶方程组,数值算例用来检验该方法的精度和有效性.

Camassa-Holm方程; 尖波解; 局部中心间断Galerkin法; 有限元法

1 预备知识

Camassa-Holm方程(简称C-H方程)是一类十分重要而又特别的新型浅水波方程.1981年,C-H方程由Fuchssteniner和Fokas作为具有双Hamilton结构的例子给出,随后,R. Camassa等[1]将其作为浅水波方程重新提出,并发现了具有的一些特殊性质一尖峰孤波解和Blow-up解等,由此引发了人们对C-H方程的极大兴趣.关于C-H方程的数学理论研究( 从方程的角度) 从20世纪90年代开始,众多数学家在这方面做了很多重要的研究工作,如孤立波的轨道稳定性[2-3]、强解的局部适定性[4]、尖峰孤立子形式弱解的结构[5]、C-H方程光滑孤立波是轨道稳定的[6-7]、C-H方程的孤立尖波、孤子类解、周期解[8]和行波解[9]等.

本文考虑如下的Camassa-Holm方程

ut-uxxt+3uux=2uxuxx+uuxxx,

(1)

其中u表示流体的自由表面高度,下标ut和ux分别表示对时间和空间的偏导数.关于方程(1) 的基本性质,文献[1]中有比较全面的讨论.该方程是一个非线性色散的偏微分方程,除了具有光滑解,还允许有尖波解.由于尖波解的极大值点不光滑,在计算中可能引起高频的色散误差,这是数值求解该方程的一个难点.因此数值求解C-H方程吸引了很多研究者的注意.例如,有限差分法[10-11]、有限体积法[12]、局部间断有限元法[13]、中心间断Galerkin有限元法[14]等都被使用来模拟该方程的尖波解.本文将提出一个局部中心间断Galerkin-有限元法来求解该方程.

2 数值方法

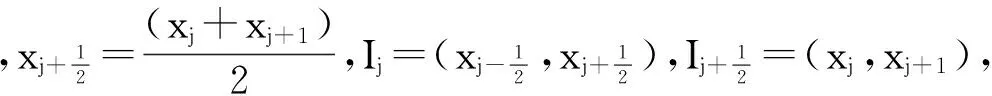
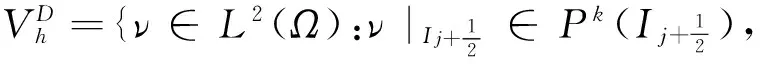
(2)

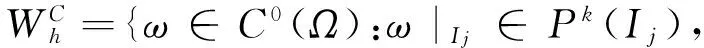
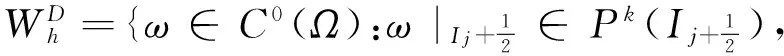
(3)

其中,Pk(I)是定义在I上的维度不超过k的多项式集合,{tn}n是对时间域的剖分,Δtn=tn+1-tn.方程(1)能够被改写为一个一阶系统

qt+f(q,u,r)x=0,

(4)

q=u-rx,

(5)

r=ux,

(6)

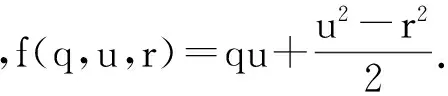
(7)

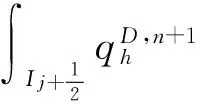
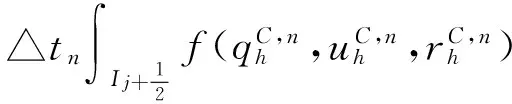
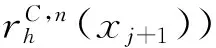
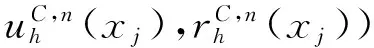
(8)

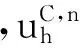
(9)

(10)

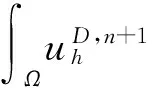
(11)

(12)

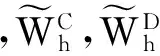
3 数值算例

在这一部分,一些数值算例被使用来检验该算法的精度和有效性.在计算中,总是使用均匀的网格剖分,网格大小为△x,时间步长△tn=0.1△x,参数θ=1.

例 1 精度测试.该算例考虑光滑行波u(x,t)=φ(x-ct),其中φ满足二阶常微分方程

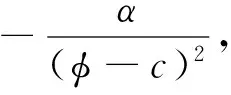
(13)

在计算中,取α=c=3,方程(13)的初始条件为φ(0)=1,φx(0)=0.由此产生了一个周期行波,周期为6.469 546 036 35.将四阶的Runge-Kutta法在100 000个节点上计算出的近似解做为参考解来计算本文算法的精度和收敛阶,如表1所示.计算结果显示了本文提出的算法对pk(k=1,2)近似具有k+1阶精度.

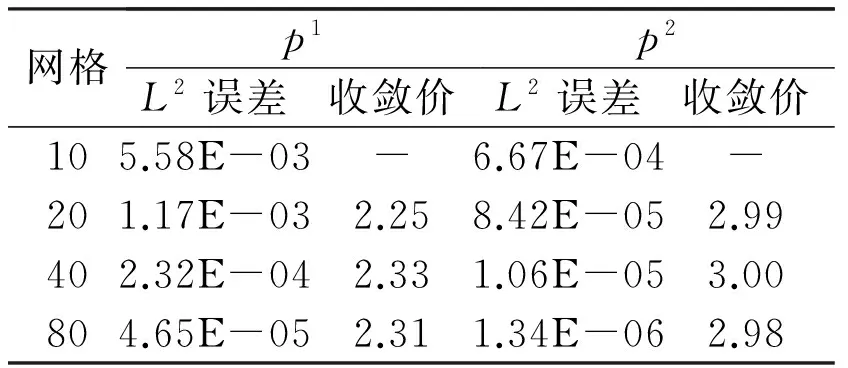
表 1 u在t=0.3时的L2误差和收敛阶 Table 3 The L2 tolerance and order of convergence while u at t=0.3

例 2 尖波解.该算例考虑了一个尖波解.初始条件为u(x,0)=φ(x,x0,α,c),其中

φ

其中,α是周期,取α=30,x0=-5和c=1,计算区域是[0,α],离散为320个均匀网格.时刻t=0,5,7.5,10的解显示在图1中.从计算结果可以看出,尖波保持得非常好,该计算结果与文献[14]的结果也吻合得比较好.

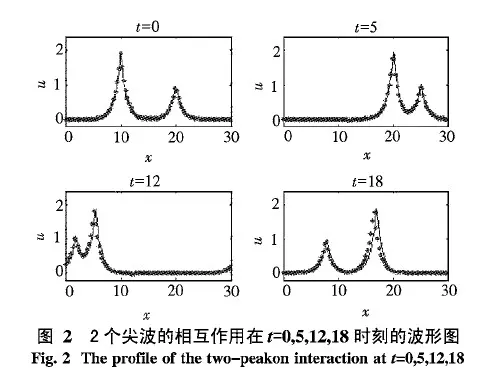
例 3 本算例研究2个尖波的相互作用,初始条件为u(x,0)=φ(x,-5,30,2)+φ(x,5,30,2).计算区域[0,30]离散为320个均匀网格.时刻t=0,5,12,18的解显示在图2中.从计算结果可以看出,2个尖波在相互作用后保持得非常好,除了尖波的位置在后期有一定的偏移,该计算结果与文献[14]的结果大体上吻合得比较好(图1～3中的点均为本文数值解,线均为文献[14]的结果).

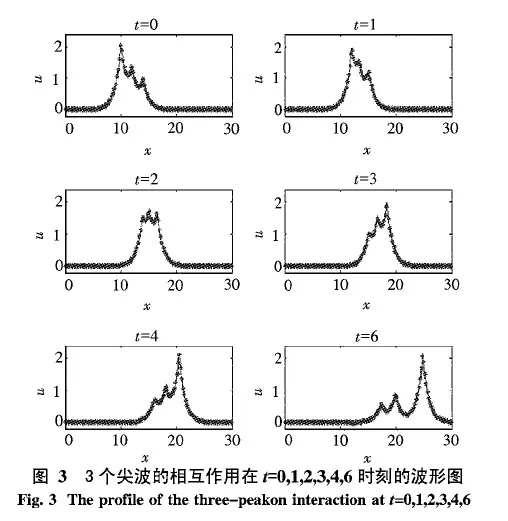
例 4 本算例研究3个尖波的相互作用,初始条件为u(x,0)=φ(x,-5,30,2)+φ(x,-3,30,1)+φ(x,-1,30,0.8).计算区域[0,30]离散为320个均匀网格.时刻t=0,1,2,3,4,6的解显示在图3中.从计算结果可以看出,3个尖波在相互作用后保持得非常好,且与文献[14]的结果吻合得非常好.

4 结论

本文提出一个高阶局部中心间断迦辽金有限元法来求解一维Camassa-Holm方程的,与文献[14]不同的是,该方法将Camassa-Holm方程改写为一个一阶方程组.数值算例检验了该方法的精度和有效性.

[1] Camassa R, Holm D D. An integrable shallow water equation with peaked solitons[J]. Phys Rev Lett,1993,71:1161-1164.

[2] Constantin A, Strauss W. Stability of peakons[J]. Commun Pure Appl Math,2000,53(5):603-610.

[3] Zhou Y. Stability of solitary waves for a rod equation[J]. Chaos Solitons Fractals,2004,21(4):977-981.

[4] Danchin R. A note on well-posedness for Camassa-Holm equation[J]. J Differ Eqns,2003,192(2) :429-444.

[5] Constantin A, Escher J. Global weak solutions for a shallow water equation[J]. Indiana Univ Math J,1998,47:1527-1545.

[6] Constantin A, Strauss W. Stability of the Camassa-Holm solitons[J]. J Nonlinear Sci,2002,12:415-422.

[7] Constantin A, Molinet L. Orbital stability of solitary waves for a shallow water equation[J]. Phys,2001,D157:75-89.

[8] 李春海,唐生强,黄文韬,等. 一类广义Camassa-Holm方程的孤立尖波、孤子类解和周期解[J]. 四川师范大学学报:自然科学版,2009,32(5):572-575.

[9] 张克磊,唐生强,王兆娟. Camassa-Holm-KP方程的行波解分支[J]. 四川师范大学学报:自然科学版,2010,33(1):58-61.

[10] Coclite G M, Karlsen K H, Risebro N H. A convergent finite difference scheme for the Camassa-Holm equation with generalH1initial data[J]. SIAM J Numer Anal,2008,46:1554-1579.

[11] 常红. Camassa-Holm方程的守恒有限差分格式[J]. 高等学校计算数学学报,2012,34(1):78-86.

[12] Artebrant R, Schroll H J. Numerical simulation of Camassa-Holm peakons by adaptive upwinding[J]. Appl Numer Math,2006,56:695-711.

[13] Xu Y, Shu C W. A Local discontinuous Galerkin method for the Camassa-Holm equation[J]. SIAM J Numer Anal,2008,46:1998-2021.

[14] Li M, Chen A. High order central discontinuous Galerkin-finite element methods for the Camassa-Holm equation[J]. Appl Math Comput,2014,227:237-245.

[15] Cockburn B, Shu C W. The Runge-Kutta discontinuous Galerkin method for conservation laws V:multidimensional systems[J]. J Comput Phys,1998,141:199-224.

2010 MSC：65M60; 35J05

(编辑 郑月蓉)

High Order Local Central Discontinuous Galerkin-Finite Element Methods for the Camassa-Holm Equation

MA Jianjun1, CHEN Aimin2, HAO Yifei1
(1.ResearchCenterforInternationalBusinessandEconomy,SichuanInternationalStudiesUniversity,Chongqing400031;2.CityCollegeofScienceandTechnology,ChongqingUniversity,Chongqing402167)

In this paper, we develop high order local central discontinuous Galerkin-finite element methods for solving the Camassa-Holm equation which supports peakon solutions. In our numerical approach, we first reformulate the Camassa-Holm equation into a conservation law coupled with a system of first order equations. Then we propose a family of high order numerical methods which discretize the conservation law with local central discontinuous Galerkin methods and the system of first order equations with continuous finite element methods. Numerical tests are presented to illustrate the accuracy and validity of the proposed schemes.

Camassa-Holm equation; peakon solutions; local central discontinuous Galerkin methods; finite element methods

2014-08-29

重庆市自然科学基金一般项目(CSTC2012JJA00005)

马健军(1983—),男,讲师,主要从事偏微分方程数值解的研究,E-mail:majianjun425@163.com

O241.82

A

1001-8395(2015)06-0871-04

10.3969/j.issn.1001-8395.2015.06.016