Bell多项式在(2+1)维Nizhnik方程组中的应用

罗天琦, 黄 欣(. 乐山师范学院 数学与信息科学学院, 四川 乐山 64000; 2. 四川财经职业学院 基础部, 四川 成都 600)



Bell多项式在(2+1)维Nizhnik方程组中的应用

罗天琦1, 黄 欣2*
(1. 乐山师范学院 数学与信息科学学院, 四川 乐山 614000; 2. 四川财经职业学院 基础部, 四川 成都 610101)

将Bell多项式方法推广到(2+1)维非线性发展方程可积性的研究.对于(2+1)维的Nizhnik方程组,构造了其双线性形式,并得出该方程组由双Bell多项式形式构成的双线性Bäcklund变换及相应的Lax对.

双Bell多项式; 双线性Bäcklund变换; Lax对; (2+1)维Nizhnik方程组

可积性属于非线性波动方程研究中的一个重要板块,背景不同的方程是否具有可积性,除了由它自身的数学结构能体现之外,与孤立子的存在性也密切相关[1-3],而孤子的发现及其深入研究大大地促进了非线性波动方程的研究与发展[4-9].由Hirota建立的双线性方法是研究非线性波动方程的一种非常有效的办法,如果一个非线性系统可以写成双线性形式,就能构造出这个非线性系统的精确解,可积性也是其处理范围,而这一方法与双Bell多项式有关联.C. Gilson等[10]扩展了由E. T. Bell[11]提出了Bell多项式的概念,将其推广到二元,变成双Bell多项式,使它能够与Hirota双线性算子联系在一起,他们建立了一套的办法,使我们通过Bell多项式,无需费力地寻找合适的双线性变换,无需大量运算,就能够直接快速找到方程的双线性形式,整个过程只需要用到普通的微分算子,量纲分析和一些基本的组合知识.通过适当的约束条件,即可以获得与双线性Bäcklund变换等价的系统.这个系统由一对Bell多项式的线性组合形式构成.近年来,E. G. Fan提出了超Bell多项式理论,给出超空间中超Bell多项式的定义,并成功将此理论用于超对称双波色子方程[12]等方程之中.

M. Boiti等[13]研究了线性谱问题

L1ψ=ψxx-ψyy-u(x,y,t)ψ=0,

(1)

其中u(x,y,t)由一个辅助算子L2来定义,L2由式子

L2ψ=ψt+F(∂x,∂y,u)ψ=0

(2)

给出,满足[L1,L2]=0,其中只有平凡局部算子L2可以与L1对易.然而在文献[14]中,Lax对条件变弱了,算子L2与L1对易只需要在谱问题

[L1,L2]ψ=0

(3)

的解的子空间里,从而得到一个三阶非线性偏微分方程

ut=-(ua)xxx+(uax)xx+(uaxx)x+

(ub)yyy+(uby)yy+(ubyy)y+

(4)

其中,a(x,t)、b(y,t)、c(x,t)、d(y,t)均为任意函数.

特别地,当a=1,b=c=d=0时,可以推出(2+1)维Nizhnik方程组

(5)

文献[15]通过用齐次平衡原则和Hirota方法求得了Nizhnik方程组的多重孤子解.在本文中,将用Bell多项式理论对(2+1)维Nizhnik方程组(5)进行讨论.

1 预备知识

在本文中需要用到的Bell多项式属于指数型的,一共分为3类,在此先回顾一些需要用到的概念和性质[10,16].

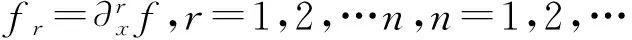
Y0(f)=1,

(6)

为一维Bell多项式,也可以将其记作Y-多项式.

根据一维Bell多项式的定义,其对应前几项表达式如下:

(7)

在(6)式中,Ynx(f)满足

其中和式取遍n=c1+2c2+…+ncn的所有整数分划.

下面将列出Bell多项式的一些性质,这些性质是Bell多项式的基础,它们使得Bell多项式和Hiota线性算子联系在一起.

性质 1 Bell多项式(6)满足如下递推公式

Yn+1(f1,f2,…,fn+1)=

(∂x+f1)Yn(f1,f2,…,fn),Y0=1.

(9)

性质 2

Yn[-f1,f2,…,(-1)nfn]=

(-1)nYn(f1,…,fn).

(10)

性质 3Y-多项式满足如下加法公式

).

(11)

命题 1 对于指数函数F=ef和G=eg,其中f=f(x),g=g(x),根据双线性算子的定义

Dx(f·g)=(∂x-∂x′)f(x)g(x′)|x=x′=

fxg-fgx.

可以得到

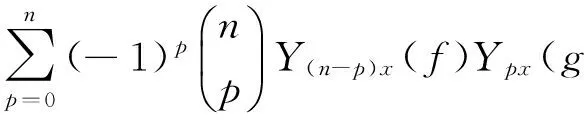
(12)

证明 由双线性算子定义式可知

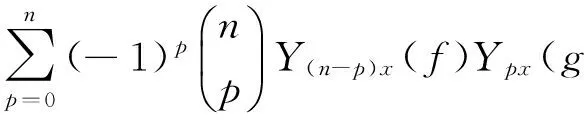
(13)

性质 4 基于加法公式(11)与恒等式(12),取

(y1,…,yn)=(f1,…,fn),

则下列等式成立

Yn(y1,…,yn)|ym=fm+(-1)mgm=

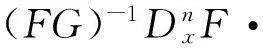
(14)

定义 2 通过变量替换

w=f+g,v=f-g,

可以得到一维双Bell多项式:

Ynx(v,w)=Ynx(f1,f2,…,fn),

(15)

其中

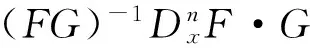
(16)

其中,v=lnF/G,w=lnFG.

根据一维双Bell多项式的定义,其对应前几项表达式如下:

Yx(v,w)=vx,

Y5x(v,w)=v5x+10v3xw2x+5vxw4x+

(17)

利用(10)和(11)式可知

Y(v,w)=Ynx[v,v+(w-v)]=

Ynx[v,v+(w-v)]|(w-v)2j+1=0=

(18)

根据上述性质,再结合比对一维双Bell多项式由于其奇偶阶不同得到的结论不同,需要引入P-多项式的概念.

定义 3 令q=w-v,则可以将偶数阶的一维Y-多项式表达成如下形式

P2nx(q)=Y2nx(0,q).

(19)

上式又称为一维P-多项式.

根据一维P-多项式的定义,其对应前几项表达式如下:

P0(q)=1,

P2x(q)=q2x,

(20)

将(19)式代入(18)式可以得到

(21)

由此可见Y-多项式能够用Y-多项式和P-多项式的组合形式表达出来.

除此之外,若令q=2lnG,根据(16)和(19)式容易看出P-多项式与Hirota双线性算子之间存在恒等式

(22)

定义 4 令f=f(x1,…,xn)是定义在C∞上的多变量函数,下面的指数多项式

Yn1x1,…,nlxl(f)≡Yn1,…,nl(fr1x1,…,rlxl)=

(23)

叫做多维Bell多项式,也可以称为广义Bell多项式或者多维Y-多项式.其中定义

r1=0,…,n1;…;rl=0,…,nl.

根据多维Bell多项式的定义可知,对于简单的情形f=f(x,t)时,对应的二维Bell多项式的前几项表达式为:

Yx,t(f)=fx,t+fxft,

Y3x,t(f)=f3x,t+3f2x,tfx+3fx,tf2x+

(24)

定义 5 假定w=f+g,v=f-g,则多维的双Bell多项式可以被定义为如下形式

Yn1x1,…,nlxl(v,w)=Yn1x1,…,n1xl(f)=

Yn1,…,nl(fr1x1,…,rlxl),

(25)

其中

上式又称为多维Y-多项式.根据多维双Bell多项式的定义,可以得到其常用的低阶表达式为

Yx(v,w)=vx,

Yx,t(v,w)=wxt+vxvt,

Y3x,t(v,w)=w3x,t+3v2x,tvx+3wx,tw2x+

(26)

Yn1x1,…,nlxl(v=lnF/G,w=lnFG)=

(27)

其中n1+n2+…+nl≥1.

当G=F时,通过恒等式(27),可以得出多维P-多项式的形式为

Yn1x1,…,nlxl(0,q=2lnF)=

(28)

根据多维P-多项式的定义,当q=q(x,t)时,可以推导出常用的几项表达式如下

P0(q)=1,

P1x,1t(q)=qxt,

P3x,1t(q)=q3x,t+3qx,tq2x,

P5x,1t(q)=q5x,t+5qx,tq4x+

(29)

恒等式(27)和定义式(28)在连接非线性方程和它们对应的双线性形式上,是特别有用的.这意味着假如一个非线性系统能够被写成P-多项式的线性组合,那么它就能转化为对应的双线性方程.此后,就可以根据双线性形式构造给定方程的Wronskian解、孤子解、有理解、拟周期解……在得出给定方程的P-多项式线性组合之后,通过Y-多项式和P-多项式之间的关系,可以推出给定方程的一些可积性质,比如双线性Bäcklund变换、Lax对、守恒律等,这些性质对于方程的研究是非常重要的.

定理 1 多维Y-多项式可以被分离成为多维P-多项式和多维Y-多项式的组合形式

Yn1x1,…,nlxl(v,w)|v=lnF/G,w=lnFG=

Yn1x1,…,nlxl(v,v+q)|v=lnF/G,q=2lnG=

Y(n1-r1)x1,…,(nl-rl)xl(v).

(30)

其中n1+…+nl为偶数.

在Hopf-Cole变换(v=lnψ)的作用下,多维Bell多项式具有如下性质

(31)

这意味着多维双Bell多项式Yn1x1,…,nlxl(v,v+q)能够被线性化,

Yn1x1,…,nlxl(v,v+q)|v=lnF/G,q=2lnG=

ψ(n1-r1)x1,…,(nl-rl)xl.

(32)

这会是找到非线性方程对应Lax系统的快捷方法.

通过(5)式,Y-多项式型Bäcklund变换能够直接线性化为如下Lax对

(33)

2 (2+1)维Nizhnik方程组的双线性形式

为找出方程(5)的可双线性化形式,做尺度变换

x→λx,y→λky,t→λαt,

u→λβu,v→λγv,

(34)

则原方程变为

λβ-αut+λβ-3uxxx+3λβ+γ-1(uv)x=0,

λβ-1ux=λγ-kvy.

(35)

发现方程在变换

x→λx,y→λy,t→λ3t,

u→λ-2u,v→λ-2v,

(36)

之下保持不变.由此,令

u=c(t)qxy,

(37)

引入势函数q,其中c=c(t)是关于变量t的任意函数.

将(37)式代入(5)式可得

E(q)=cqx,y,t+cq4x,y+3c2(qxyq2x)x=0. (38)

关于x积分一次

E(q)=cqy,t+cq3x,y+3c2qxyq2x=0.

(39)

如果令c(t)=1,方程(39)就能写成P-多项式的组合形式:

E(q)=Pyt(q)+P3x,y(q).

(40)

通过变换

q=2lnF,

可得

u=qxy=2(lnF)xy.

结合P-多项式的形式和关系式(27)和(28),可以得到原方程的双线性形式

(41)

根据这个双线性方程,就能获得原方程的精确解,包括多孤子解.这个结果与用Hirota方法直接做变换双线性化的结果一致,这里不再作更多讨论.

3 (2+1)维Nizhnik方程组的双线性Bäcklund变换和Lax对

定理 2 通过双Bell多项式,可以得出原方程组(5)的双线性Bäcklund变换为

(DxDy+αDx-λ)F·G=0.

(42)

证明 假定方程(39)有2个不同的解,分别为q′和q,则(39)式对应的双条件如下:

(q′-q)y,t+(q′-q)3x,y+

(q′+q)xy(q′-q)2x]=0.

(43)

很明显系统(43)反映了方程(39) 2个不同解q′和q之间的联系,若能把系统(43)在一定的约束条件下转化成为2个使原式成立的条件,就能得到原方程的双Bäcklund变换,如何寻找到合适的约束条件也正是难点所在.为了找到这个约束条件,考虑引入2个新变量

(44)

将(44)式代入(43)式,就可以得到双条件(43)的新形式

E(q′)-E(q)=

2(vy,t+v3x,y+3v2xwxy+3w2xvxy)=

2∂y[Yt(v)+Y3x(v,w)]+R(v,w)=0,

(45)

其中

R(v,w)=6Wron[Yxy(v,w),Yx(v)].

(46)

选取约束条件

Yxy(v,w)+αYx(v)=λ,

(47)

其中,α,λ为任意常数.在条件(47)的约束之下,(45)式可以变成如下形式

∂y[Yt(v)+Y3x(v,w)+3λYx]=0.

(48)

因此,得到了一个关于Y-多项式的如下耦合系统

Yt(v)+Y3x(v,w)+3λYx+ξ=0,

Yxy(v,w)+αYx(v)-λ=0,

(49)

其中ξ为任意积分常数.由此可得原方程组(5)的双线性Bäcklund变换为

(DxDy+αDx-λ)F·G=0.

证毕.在此之后,可以通过选取种子解,进而得到原方程的多孤子解,此处不再详述.

定理 3 通过双Bell多项式,可以得出原方程组(5)的Lax系统为

L1ψ=ψxy+uyψ+αψx-λψ,

L2ψ=ψt+ψ3x+3uxψx+3λψx.

(50)

证明 通过Hopf-Cole变换

v=lnψ,

再根据(31)式可得

(51)

将(51)式代入(4)式,可以得到线性系统

(L1-λ)ψ=(∂x∂y+qxy+α∂x)ψ,

(∂t+L2)ψ=(∂t+∂3x+3q2x∂x+3λ∂x)ψ.

(52)

进而可以得到方程的Lax系统

L1ψ=ψxy+uyψ+αψx-λψ,

L2ψ=ψt+ψ3x+3uxψx+3λψx.

(53)

根据相容性条件ψxyt=ψtxy容易验证可积性条件

[L1,L2]ψ=0

(54)

成立,系统(53)是目标方程组的Lax对.证毕.

4 结语

本文将Bell多项式方法推广到(2+1)维非线性发展方程可积性的研究.对于(2+1)维的Nizhnik方程,构造了其双线性形,并得出该方程组由双Bell多项式形式构成的双线性Bäcklund变换及相应的Lax对.目前在Bell多项式和Hirota方法结合方面的工作目前主要体现在利用Bell多项式方法研究KdV、KP、Burgers等方程的可积性质,而这些方程Lax对是已知的,并且主要局限于空间一维或二维的非线性方程.但对未知Lax对的高阶非线性方程,特别是利用Bell多项式研究耦合的演化方程、非等谱方程、离散方程和超对称方程方面的工作有待去进一步研究.

[1] 李翊神. 孤子与可积系统[M]. 上海:上海科技教育出版社,1999.

[2] 谷超豪. 孤立子理论与应用[M]. 杭州:浙江科学技术出版社,1990.

[3] 谷超豪,胡和生,周子翔. 孤立子理论中的达布变换及其几何作用[M]. 上海:上海科学技术出版杜,2005.

[4] 刘倩,周钰谦,刘合春. 广义Hirota-Satsuma耦合KdV方程的精确解[J]. 四川师范大学学报:自然科学版,2011,34(3):335-339.

[5] 李晓光,黄欣,陈丹. 二维空间中一类非线性Schrödinger方程爆破解的集中性质[J]. 四川师范大学学报:自然科学版,2010,33(6):745-749.

[6] 舒级. 一类带调和势的随机非线性Schrödinger方程的爆破解[J]. 四川师范大学学报:自然科学版,2011,34(6):906-910.

[7] 黄欣,蒲志林. Bose-Einstein凝聚中一类非线性Schrödinger方程的门槛条件[J]. 应用数学:2008,21(4):650-655.

[8] 陈光淦. 一类带动力边值的随机抛物型偏微分方程的不变叶理[J]. 四川师范大学学报:自然科学版,2012,35(1):137-142.

[9] 邓艳萍,周钰谦. 非线性Schrödinger方程组初值问题的驻波解[J]. 四川师范大学学报:自然科学版,2013,36(2):243-246.

[10] Gilson C, Lambert F, Nimmo J, et al. On the combinatorics of the HirotaD-operators[J]. Proc Royal Soc,1996,A452:223-234.

[11] Bell E T. Exponential polynomials[J]. Ann Math,1934,35(2):258-277.

[12] Fan E G. New bilinear Bäcklund transformation and Lax pair for the supersymmetric Two-Boson equation[J]. Studies in Applied Mathematics,2011,127(3):284-301.

[13] Boiti M, Leon J P, Manna M, et al. On the spectral transform of a Korteweg-de Vries equation in two spatial dimensions[J]. Inverse Problems,1986,2:271-279.

[14] Radha R, Lakshmanan M. Singularity analysis and localized coherent structures in (2+1)-dimensional generalized Korteweg-de Vries equations[J]. J Math Phys,1994,35:4764.

[15] Wang M L, Li X Z, Han S X. A nonlinear transformation and multi-soliton solutions to the Nizhnik equation[J]. Mathematica Applicata,2005,18(2):225-231.

[16] Lambert F, Springael J. Classical Darboux transformations and the KP hierarchy[J]. Inverse Problems,2001,17(4):1067-1074.

2010 MSC：35Q53

(编辑 周 俊)

Bell Polynomial Application in (2+1)-Dimensional Nizhnik Equations

LUO Tianqi1, HUANG Xin2
(1.CollegeofMathematicsandInformationScience,LeshanNormalCollege,Leshan614000,Sichuan;2.DepartmentofBasicCourses,SichuanFinanceandEconomicsVocationalCollege,Chengdu610101,Sichuan)

In this paper, we generalize the Bell polynomial method to investigate the integrable property for the (2+1)-dimensional nonlinear evolution equations. Then using this method, we construct the bilinear form to derive the Bäcklund transformations in the form of the binary Bell polynomials and the corresponding Lax pair for the (2+1)-dimensional Nizhnik equations.

binary Bell polynomial; bilinear Bäcklund transformation; Lax pair; (2+1)-dimensional Nizhnik equations

2015-06-29

四川省应用基础研究计划项目(2013JYZ014)和四川省教育厅自然科学基金(14ZB0413)

O175.24

A

1001-8395(2015)06-0861-06

10.3969/j.issn.1001-8395.2015.06.014

*通信作者简介：黄 欣(1980—),女,讲师,主要从事非线性偏微分方程的研究,E-mail:huangxinnv@163.com