运用双因素方差分析法分析水处理实验数据

吴俊奇， 李 庚， 马龙友

(北京建筑大学 环境与能源工程学院， 北京 100044)

实验技术与方法

运用双因素方差分析法分析水处理实验数据

吴俊奇， 李 庚， 马龙友

(北京建筑大学 环境与能源工程学院， 北京 100044)

运用数理统计的双因素方差分析法分析水处理实验数据，比仅用单因素方差分析法可获得更多更全面的规律信息，有助于水处理实验的深入研究。通过运用双因素无重复实验的方差分析法对某组混凝沉淀实验数据进行实例分析，结果表明此分析方法可得出两种因素对实验结果的影响显著性,还可以得出两种因素的交互作用对实验结果的影响显著性，并可根据显著性大小分析出因素的主次顺序。

混凝沉淀; 实验数据处理； 方差分析； 显著性检验

在给排水科学与工程专业中，混凝沉淀实验是水质工程学课程中的主要实验之一[1-2]。在给水处理中混凝沉淀实验可考察不同混凝药剂及其与水样反应时间长短对水中胶体和悬浮性杂质的去除效果[3]，在污水处理中它主要是考察不同药剂及其与水样反应时间长短对污水中有机物的去除效果[4]。通过混凝沉淀实验取得的最佳混凝药剂和反应时间是水处理构筑物设计的基本参数，可用于指导工程设计[5-6]。因此混凝沉淀实验往往要考虑多种因素及多个水平，需要进行大批量的组合实验。在实验设计时可采用单因素实验设计、双因素实验设计、多因素正交试验设计、均匀设计等方法[7-9]，选用的设计方法的不同，则其实验组数亦不同，且数量上会有非常大的差距。当确定实验设计方法并取得实验数据后，还需要对实验数据进行分析，如单因素方差分析、双因素方差分析、回归分析等[10-12]。对实验数据进行多种形式的分析，可以从实验数据中获得更多更全面的规律信息，达到指导科研和生产的目的。运用数理统计的双因素方差分析法[13]分析水实验数据，比仅用单因素方差分析法会更有助于水处理实验的深入研究。下面通过实例，说明运用双因素方差分析法分析水处理实验数据所起的作用。

1 运用双因素无重复实验的方差分析法分析水处理实验数据

为治理环境，节约水资源，对某种污水进行回收重复使用前安排混凝沉淀实验[14]，研究药剂种类、反应时间对评价指标——出水COD的影响。药剂种类取了3个水平，反应时间取了3个水平。对两因素的各水平的每对组合做实验，组成9个实验，得到的出水COD见表1。表1中：A表示药剂，A1为FeCl3，A2为Al2(SO4)3,A3为FeSO4;B代表反应时间，B1为3 min,B2为5 min，B3为1 min。

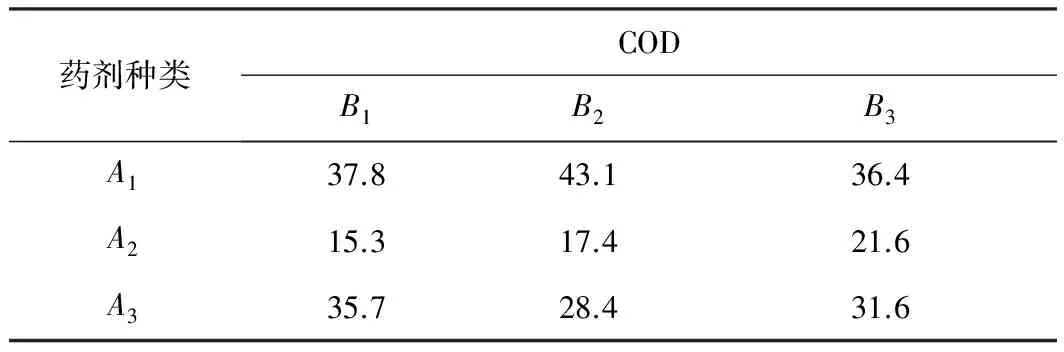
表1 出水COD数据 mg/L

取显著性水平α=0.05和α=0.01，运用双因素无重复实验的方差分析法，分析药剂种类和反应时间对出水COD影响的显著性，基本步骤如下：

(1) 根据表1列出实验数据计算行和列见表2。表中，Ti为行和，Tj为列和，Tij=267.3。

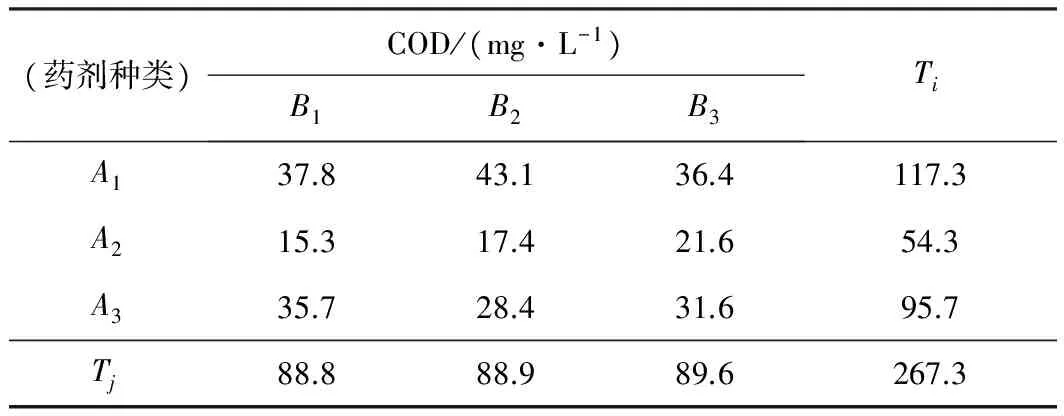
表2 实验数据计算表

(2) 计算各偏差平方和

总偏差平方和ST：

因素A偏差平方和SA：

因素B偏差平方和SB：

误差平方和SE：

SE=ST-SA-SB=755.62-683.28-0.13=72.21

(3) 计算各偏差平方和的自由度。ST的自由度为fT=3×3-1=8，SA的自由度为fA=3-1=2,SB的自由度为fB=3-1=2,SE的自由度为fE=fT-fA-fB=8-2-2=4

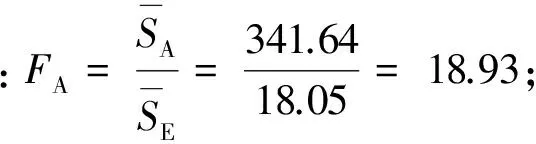
(6) 显著性检验。由F分布表查得临界值：F0001(fA,fE)=F0.01(2,4)=18.00;F0.05(fB,fE)=F0.05(2,4)=6.94

由于FA=18.93>18.00=F0.01(2,4)，故认为因素A对实验结果有高度显著性影响，即药剂种类对出水COD有高度显著影响，记为“**”。

由于FB=0.0036<6.94=F0.05(2,4)，故认为因素B对实验结果的影响不显著，即反应时间对出水COD的影响不显著。

以上分析得到，两种因素对出水COD影响是不同的，应更重视药剂种类对出水COD的影响，这就体现了应用双因素无重复实验方差分析的作用。

(7) 列出双因素无重复实验方差分析表,见表3。

表3 双因素无重复实验方差分析表

2 运用双因素重复实验的方差分析法分析水处理实验数据

为了研究投药量与混合时间及它们的交互作用对出水浊度影响，进行直接过滤实验。投药量取3个水平，混合时间取3个水平，相互组合，组成9个实验，每个实验都做2次，得到的出水浊度见表4。

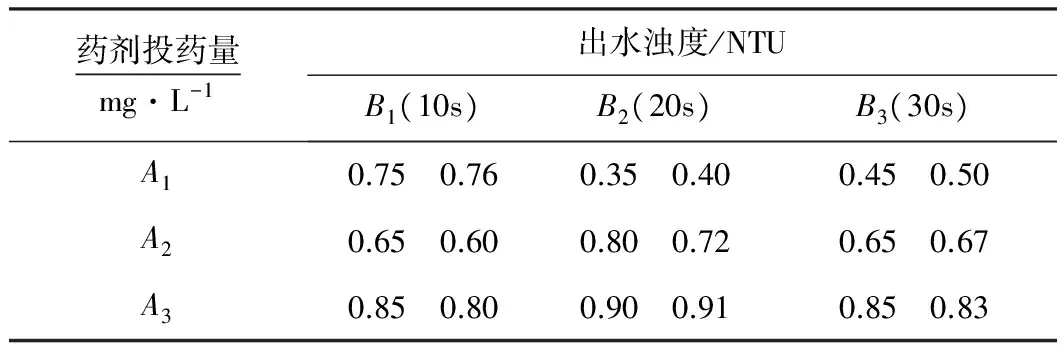
表4 出水浊度数据表

取显著性水平α=0.01，运用双因素重复实验方差分析法，分析投药量与混合时间以及它们的交互作用对出水浊度影响的显著性，基本步骤如下：

(1) 根据表4列出的实验数据计算见表5。

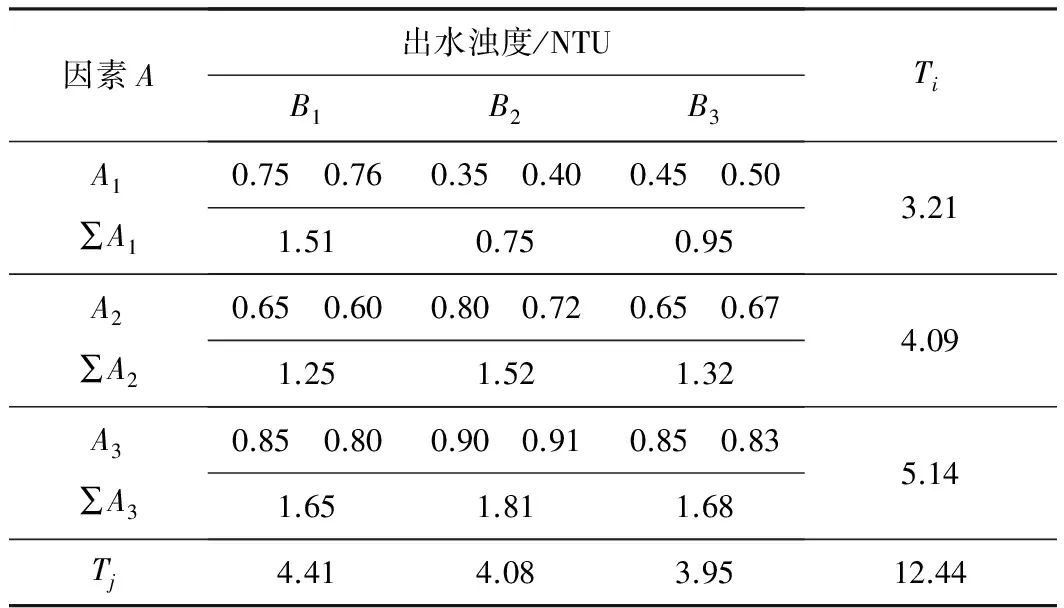
表5 实验数据计算表

(2) 计算各偏差平方和

总偏差平方和ST：

因素A偏差平方和SA：

因素B偏差平方和SB：

误差平方和SE：

9.0994-9.0907=0.0087

交互作用偏差平方和SA×B：

SA×B=ST-SA-SB-SE=0.163 3

(3) 计算各偏差平方和的自由度。总偏差平方和ST的自由度为：fT=3×3×2-1=17；SA的自由度为fA=3-1=2；SB的自由度为fB=3-1=2；SE的自由度为fE=3×3(2-1)=9；SA×B的自由度为fA×B=fT-fA-fB-fE=4

(4) 计算各平均偏差平方和：

(5) 计算F值及显著性检验

① 计算各F值：因素A的F值为

因素B的F值为

交互作用的F值为

② 显著性检验。给定显著性水平α=0.01，查F分布表，得临界值：

F值与临界值相比较，可得：

FA=155.6>8.02=F0.01(2,9)

FB=155.6>8.02=F0.01(2,9)

上面3个F值都大于临界值，这说明因素A(投药量)、因素B(混合时间)，以及因素A与B的交互作用A×B对出水浊度都有高度显著影响，记为“**”。

一般说来，F值与临界值之间的差距越大，说明该F值对应的因素或交互作用对实验结果影响越显著，或者说该因素或交互作用越重要。从F值的大小可以排出因素的主次顺序：因素A(投药量)最重要，依次是交互作用A×B和因素B(混合时间)。通常把交互作用A×B也看作是影响实验结果的因素。

从本例分析中得到：两因素(投药量和混合时间)以及它们的交互作用对出水浊度都有显著性影响，都是不可忽视的重要因素；还可分析出因素的主次顺序：因素A(投药量)→交互作用A×B→因素B(混合时间)。

这就是应用双因素重复实验方差分析得出的结果。

(6) 列出双因素重复实验方差分析表，见表6。

表6 双因素重复实验方差分析表

3 结束语

上面两例应用数理统计的双因素实验方差分析法，分析了水处理的实验数据，获得了有用的信息和结果，有助于对实验进一步深入了解。

References)

[1] 李圭白，张杰.水质工程学[M].北京:中国建筑工业出版社，2005.

[2] 许保玖，龙腾锐.当代给水与废水处理原理[M].北京：高等教育出版社，2000.

[3] 严煦世，范瑾初.给水工程[M].4版.北京：中国建筑工业出版社，1999.

[4] 张自杰.排水工程[M].4版.北京：中国建筑工业出版社，2000.

[5] 崔玉川，员建，陈宏平.给水厂处理设施设计计算[M].北京：化学工业出版社，2003.

[6] 崔玉川，刘振江，张绍怡.城市污水厂处理设施设计计算[M].北京：化学工业出版社，2003.

[7] 栾军.现代试验设计优化方法[M].上海：上海交通大学出版社，1995.

[8] 方开泰.均匀设计与均匀设计表[M].北京：科学出版社，1994.

[9] 华罗庚.优选学[M] .北京：科学出版社，1981.

[10] 陈魁.试验设计与分析[M].2版.北京：清华大学出版社，2006.

[11] 洪伟，吴承祯.试验设计与分析[M].北京：中国林业出版社，2004.

[12] 盛骤，谢式千，潘承毅.概率论与数理统计[M] .北京：高等教育出版社，2010.

[13] 耿素云，张立昂.概率统计[M].北京：北京大学出版社，2004.

[14] 吴俊奇，李燕城.水处理实验技术[M].3版.北京:中国建筑工业出版社，2009.

Using two-factor variance analysis to processdata of water treatment experiment

Wu Junqi, Li Geng, Ma Longyou

(School of Environment and Energy Engineering,Beijing University of CivilEngineering and Architecture,Beijing 100044,China)

Using the two-factor variance analysis method to analyze the data of water treatment experiment is better than only using the single factor variance analysis method. It can obtain more comprehensive information to contribute to the further research of water treatment experiment.By using the two-factor variance analysis for no-repeated experiment to process the data of a certain set of coagulation and sedimentation experiments, it shows that this analysis method can conclude the significance of the two factors on the result of the experiment.By using two-factor variance analysis method for repeated experiment to process the data of a certain set of filtration experiment, it shows that this method can conclude not only the significance of the two factors on the result, but also the significance of the interaction of the two factors and the order of importance of these factors according to the significance.

coagulation and sedimentation; experimental data processing; variance analysis; significance test

2014- 10- 14 修改日期：2014- 12- 19

吴俊奇(1960—)，男，北京，工学硕士，教授，硕士生导师，主要研究方向为水处理实验技术

E-mail：wujunqi@bucea.edu.cn

TU991.22;N37

A

1002-4956(2015)5- 0042- 03