基于主成分分析的帕金森量表优化

雷少正 王崇骏 谢俊元

(1.南京大学计算机科学与技术系，南京，210023；2.南京大学软件新技术国家重点实验室，南京，210023)



基于主成分分析的帕金森量表优化

雷少正1,2王崇骏1,2谢俊元1,2

(1.南京大学计算机科学与技术系，南京，210023；2.南京大学软件新技术国家重点实验室，南京，210023)

西医量表是评估帕金森病(Parkinson′s disease,PD)的重要依据，而这些量表包含大量交叉重复问题，不利于快速评估帕金森病。因此，优化这些西医量表对快速诊断帕金森病有非常重要的意义。针对该问题，提出了基于主成分分析(Principal component anaysis, PCA)的量表问题的优化算法。本文提出的算法先是基于主成分分析提取出加权投影向量，然后在投影向量的基础上采用基于大津阈值(Otsu)局部递归分割算法划分量表，最后基于贡献度因子(Contribution factor, CF)设计新量表。实验通过采用支持向量机(Support vector machine,SVM)识别帕金森病，发现用仅占原西医量表总问题数的21%的新量表能达到与原量表相当的识别水平。

帕金森病; 量表优化; 主成分分析; 大津阈值局部递归分割; 加权投影向量; 贡献度因子

引 言

帕金森病[1-4]是一种常见于中老年人群的中枢神经系统变性疾病，首先由英国医生James Parkinson在一篇《震颤麻痹》的论文中进行了描述性研究，该病会致使患者出现如下症状：四肢颤抖、肌肉僵直、行动迟缓、步伐拖曳、忧郁及痴呆等[5]。量表是一种试图确定主观的或者抽象概念的定量化测量的程序，对事物的特性变量可以用不同的规则分配数值。西医量表是评估帕金森病的重要手段[6-7]，然而西医量表包含大量交叉重复的量表问题，不利于医生快速诊断帕金森病。因此，优化帕金森量表对帕金森病的进一步深入研究具有重要的意义。一般在首次诊断帕金森量表时，会对所有的西医量表进行全面测评，以便从整体上评估帕金森病。目前西医量表都是从评估某一种症状而设计的，并没有从帕金森病全局的视角上设计评估标准，导致了许多量表有很多交叉重复的量表问题。在这种情况下就会导致有些重复出现的量表问题会被反复测评，或者有些量表问题对实际的测评结果影响很小。目前关于帕金森量表的研究主要是针对某一特定症状进行研究，采用数据挖掘的方法从统计特征上来研究量表至今还没有受到重视，而本文试图从这一视角来优化帕金森病量表。本文提出的基于主成分分析的量表优化方法，主要是通过降低数据的噪声和冗余来优化帕金森病的西医量表。

1 基于主成分分析的帕金森量表优化算法框架

西医量表比中医量表具有更好地规范性，评价标准量化程度高，而且样本数据也比较丰富，基于此本文选取帕金森病的西医量表所包含的量表问题作为研究对象。本文提出了基于主成分分析的帕金森量表优化算法，该算法框架分3个阶段：(1)提取基于PCA的加权投影向量；利用PCA模型计算出投影矩阵，根据贡献效率阈值提取若干主成分，采用加权累加主成分对应的特征向量，获取一个投影向量。该投影向量分量代表原数据空间相应的量表问题权重，权重越大，代表该量表问题越重要。(2)采用基于Otsu局部递归分割法分割量表问题。基于大津阀值(Otsu)局部递归分割算法获取量表问题的分组，同一组的量表问题表示具有最相似的权重。(3)设计基于贡献度因子的新量表。利用第2阶段的分组，定义一个贡献度因子，对各个分组进行排序，根据排名设计一张新量表。

2 基于PCA的加权向量提取

主成分分析(Principal component analysis，PCA)是用原有的变量的线性组合来表示样本最主要的特征，是应用线性代数最有价值的结果之一[8-10]。文献[11]首先将该变换引入生物学领域，并重新对线性回归进行了分析；文献[12]又将PCA应用在心里测验学，把离散变量变换成无关联系数；随后文献[13]对该变换进行整理归纳，因此也被称为K-L变换。由于PCA简单无参限制的优点，使得它广泛应用在各个领域，从神经科学到计算机图形学[14]。

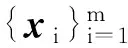
λiui=Cuii=1,…,n

(1)

式中：λi是协方差矩阵C的一个特征值;ui为相应的特征向量。

对应特征值按降序排列，当仅用前p个特征向量(p根据贡献效率选取)时，获得新的样本矩阵

Y=UTX

(2)

新的主成分即是前p个特征值，矩阵UT的列向量就是主成分对应的特征向量，各个特征向量是相互正交的。PCA可以有效地找出数据中最重要的结构，降低噪声和去除冗余，抽取隐含在复杂数据的背后的关系。基于此，本文提出了提取基于PCA的带权重的特征向量算法，该算法主要用于提取加权重投影向量，用以刻画量表问题的权重。

算法1 基于PCA的加权投影向量提取算法

输入：诊断记录的样本矩阵A，每一个行向量代表一个样本点，每一列代表一个量表问题变量；

输出：加权的投影向量v。

步骤1 对原始数据的样本矩阵A进行规范化处理，每个维度的分量按如下进行变换

(3)

步骤2 求出规范化后的样本矩阵X的协方差矩阵C。

步骤3 采用雅克比(Jacobi)迭代算法求解C的特征值λ1, …,λn，对应的特征向量为v1, …,vn。

步骤4 对特征值按降序排列得到λ1′,…,λn′，并调整对应的特征向量v1′, …,vn′。

步骤5 采用施密特(Schmitt)正交化法单位正交化特征向量得到α1, …,αn。

步骤6 计算各个主成分的累积贡献率A1, …,An,根据给定的效率阈值γ,若Ap≥γ且Ap-1<γ，则提取前p个主成分A1, …,Ap。

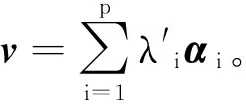
3 基于Otsu局部递归分割法划分量表

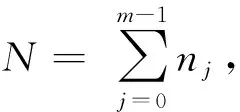
(4)

算法2描述了基于Otsu阈值的一种局部递归分割的划分量表问题的算法，按量表问题的权重分组，使得同一分组包含的量表问题的权重尽可能接近。

算法2 基于Otsu局部递归分割划分问题算法

输入：量表问题的加权投影向量v；

输出：量表问题的分割阈值集合T以及对应的量表问题分组集合Q。

步骤1 对特征向量v的元素按降序排列w，并对其按式(1-3)进行归一化，得到向量s。

步骤2 针对规范化的向量s，把该代表量表问题权重的向量s的元素投射到区间[0, 250]上，并进行频数统计，得到一个频数数组H。

步骤3 计算频数数组H所包含的量表问题数目n。

步骤4 如果n大于阈值p,则转到步骤5，否则，则转到步骤7。

步骤5 对频数数组H按式(4)求Ostu阈值τ，记录阈值τ划分H得到的两个分组H1,H2，并把该阈值加入到阈值集合T中。

步骤6 对于获得的分组H1,H2，分别计算其所对应的量表问题数n1,n2，转至步骤4。

步骤7 对阈值集合T进行排序，按照阈值对特征向量进行分组，并把对应的量表问题序号分配到对应的分组Q中。

4 实验结果与分析

4.1 实验数据及其环境

实验数据来源于某脑科医院2008—2013年之间的患者测评的量表数据。这里选取测评参与人数最多的15张西医量表，其中包含统一帕金森量表、汉密顿焦虑量表、汉密顿抑郁量表、抑郁自评量表、焦虑自评量表、帕金森睡眠量表、日常生活量表、MOCA量表、PDNMS问卷量表、帕金森随访量表以及运动并发症量表等，总共包含337个量表问题，参与测评人数为3 620。

过滤掉参评人数低于100的量表问题，余下245个量表问题。另外，有些患者单次诊断参与评估的量表问题数也很少，这里把参与评估的量表问题数低于总数的70%的患者也过滤掉，最终留下了样本数为1 122。余下的不完整的数据，采用量表问题的正常值取代空值。为便于分析，把所有的量表问题进行统一编号，预处理后的输入样本矩阵为1 122×245。实验环境为：处理器Intel(R)Pentium(R)G640 2.8GHz，内存2GB，硬盘500GB，操作系统Windows7 32位旗舰版，编程平台为MatlabR2012a，并采用了Matlab的模式识别工具箱PRtools。

4.2 量表问题权重的实验分析

采用算法1对样本进行主成分分析，得到主成分累积贡献率如图1所示。从图中可以看到前60个主成分的累积贡献率达到75%。这里选取前60个主成分作为有效主成分，由此计算出加权投影向量。这个向量的每个元素与原样本矩阵的量表问题编号相对应，向量的元素代表相应量表问题的贡献度。表1列出了贡献度排前20的量表问题，从表中可以看出，这些量表问题主要来自于抑郁自评量表、焦虑自评量表及统一帕金森量表。经脑科医院的帕金森病研究专家认定，这些问题明显与帕金森的典型症状相关，在评估帕金森病相关症状时具有重要作用。

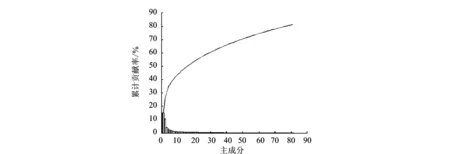
图1 主成分的累积贡献率Fig.1 Cumulative contribution rate based on PCA

表1 贡献度Top20的量表问题

4.3 量表问题分割的实验分析

利用算法2对4.2节获得的加权投影向量进行Otsu阈值分割，得到107个分组。为了比较每个分组的重要性，定义一种贡献度因子

(5)

(6)

按照式(6)计算样本的单位量表问题分值，并求出每个分组的均值和方差的无偏估计量，然后按式(5)计算出相应分组的贡献度因子。

表2为量表贡献度因子前20的问题分组。实验中的量表问题编号的命名规则为原量表编号+问题序号，而47, 48, 49分别为UPDRS第2、第3、第4分量表，7为PDNMS问卷量表，4为PDSS量表，10为MOCA量表。可以看出，UPDRS量表对应的问题所占的比重最高，而评估帕金森病最重要的量表就是统一帕金森量表(UPDRS)[18-19]。

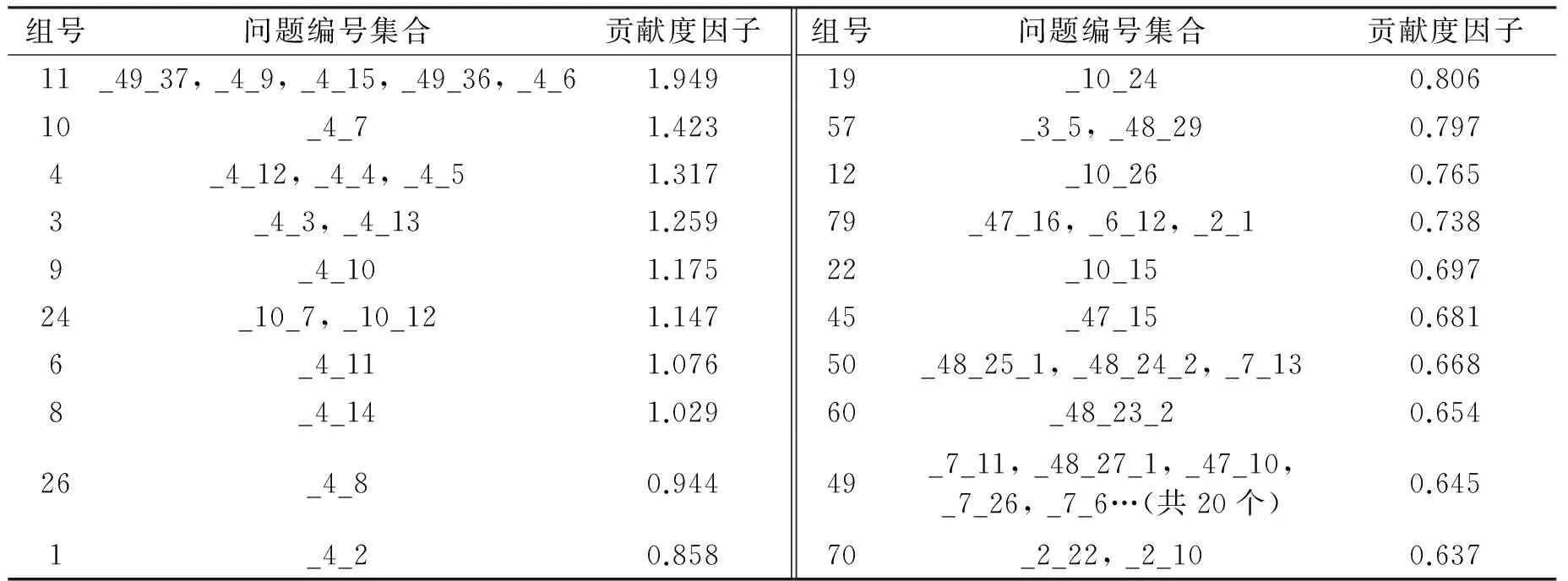
表2 贡献度因子Top20的量表问题分组

本文把贡献度因子排名前20的量表问题组合并成一张新的大量表，共计53个量表问题，占总问题数的21%。针对这张新量表，这里随机抽取原始数据库中的200条诊断记录，评估的分值占总量表问题数的比例见图2，其中均值为0.6，方差为0.013。

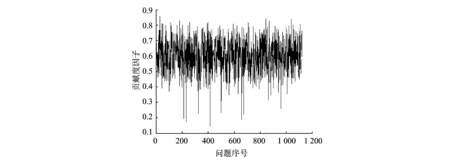
图2 新量表评估的分值占比Fig.2 Scores accounting of the new sacle

4.4 新量表识别帕金森病的实验分析

为了验证新量表识别帕金森病的效果，本文采用SVM对病人是否患帕金森病进行分类，并与原量表进行对比。SVM是基于风险结构最小化原理来提高学习系统的泛化能力的，能够采用较少的样本达到较好地分类效果[20-22]。

实验中采用的SVM的参数设置如下：核函数为径向基函数,Gamma设为1/2。表3为SVM在新量表和原量表上识别帕金森病的实验结果。

表3 SVM识别帕金森病的结果

实验结果表明：针对识别帕金森病的分类问题，SVM分类器在新量表的准确率(Precision)和召回率(Recall)都略低于原量表相应的准确率和召回率。这说明了新量表能达到与原量表识别帕金森病的相当的水平。注意到新量表的问题数仅占西医量表总问题数的21%，这为医生快速诊断帕金森病提供了一种新的思路。

5 结束语

本文提出了基于主成分分析的帕金森量表优化算法框架，利用了主成分分析可以去除复杂数据的噪声和冗余的特性，进而设计了一种基于贡献度因子概念的新量表，最后采用SVM分类器对新量表的识别帕金森病的能力进行了验证，发现新量表能够达到与原量表识别帕金森病的相当的水平。该算法框架可以为医生从全局上快速把握帕金森病提供了一种新的思路。帕金森病的量表研究在传统上一直以单一症状诊断为核心设计量表，缺乏全局的量表设计，导致了量表之间的有些问题重复出现，或者相似程度很高，不利于医生在首次快速判断帕金森病。而本文基于PCA设计的新量表在一定程度上可以快速诊断帕金森病。值得注意的是，本文设计的新量表只是在医生首次诊断帕金森病有帮助，因为新量表设计的目的是为医生从全局上把握帕金森病。如果需要进一步确定病人在某一些特定症状的轻重，还需要病人去评估传统的针对帕金森病单一症状设计的量表。本文接下来需要对新量表进行修正，新量表评估的分值并没有达到与原量表的识别帕金森病的水平。注意到贡献度因子仅仅考虑了量表问题分组的均值和方差，并没有考虑不同量表之间的差异性，量表之间并不是对等的关系，未来尝试对不同量表提出一种统一的评判标准。另外，由于原始数据存在缺失，采用过滤和正常值取代法并不是一个合理的手段，未来也需要研究直接在残缺的数据上做主成分分析的算法，同时考虑中医量表，以使得最终设计的新量表能达到较高的识别帕金森病的水平。

[1] Cummings J L. Depression and Parkinson′s disease: A review[J].The American Journal of Psychiatry, 1992, 12(1): 55-74.

[2] Barbeau A.L-dopa therapy in Parkinson′s disease: A critical review of nine years’s experience[J].Canadian Medical Association Journal, 1969, 101(13): 59.

[3] Twelves D, Perkins K S M, Counsell C.Systematic review of incidence studies of Parkinson′s disease[J].Movement Disorders, 2003, 18(1): 19-31.

[4] 褚玉霞,汪静.帕金森病研究进展分析[J].医学综述, 2006, 12(18): 1112-1113.

Chu YuXia,Wang Jing.An analysis of the progress in Parkinson′s disease[J].Medical Recapitulate, 2006, 12(18): 1112-1113.

[5] Parkinson J.An essay on the shaking palsy[M].London: Whittingham and Rowland for Sherwood, Neely, and Jones, 1817.

[6] 陈海波,王新德.统一帕金森病评定量表[J].中华老年医学杂志, 1999, 18(1): 61-62.

Chen Haibo,Wang Xinde.Unified Parkinson′s disease rating scale[J].China Academic Journal, 1999,18(1):61-62.

[7] 董青, 李建萍, 刘建军, 等.帕金森病患者纹状体多巴胺转运体显像与帕金森病临床量表评分的相关性[J].临床神经病学杂志, 2005, 18(3): 167-169.

Dong Qing, Li Jianping, Liu Jianjun, et al.Correlation of striatum dopamine transporter imaging and the scores of Parkinsonian clinical scale in patients with Parkinson′s disease[J].Journal of Clinical Neurology, 2005,18(3): 167-169.

[8] Smith L I.A tutorial on principal component analysis[M].New York:Cornell University, 2002.

[9] Daffertshofer A, Lamoth C J C, Meijer O G, et al.PCA in studying coordination and variability: A tutorial[J].Clinical Biomechanics, 2004, 19(4): 415-428.

[10]Geladi P, Kowalski B R.Partial least-squares regression: A tutorial[J].Analytica Chimica Acta, 1986, 185: 1-17.

[11]Pearson K.Principal components analysis[J].The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1901, 6(2): 559.

[12]Anderson T W.Harold Hotelling′s research in statistics[J].The American Statistician, 1960, 14(3): 17-21.

[13]Carayannis G, Gueguen C.The factorial linear modelling: A Karhumen-Loeve approach to speech analysis[C]//Acoustics, Speech, and Signal Processing, IEEE International Conference on ICASSP′76.Vancouver, Canada: IEEE, 1976, 1: 489-492.

[14]Karhunen J, Joutsensalo J.Representation and separation of signals using nonlinear PCA type learning[J].Neural Networks, 1994, 7(1): 113-127.

[15]Otsu N.A threshold selection method from gray-level histograms[J].System Man & Cybemetics IEEE Transaction on, 1979, 9(1): 62-66.

[16]Arifin A Z, Asano A.Image segmentation by histogram thresholding using hierarchical cluster analysis[J].Pattern Recognition Letters, 2006, 27(13): 1515-1521.

[17]Ng H F.Automatic thresholding for defect detection[J].Pattern Recognition Letters, 2006, 27(14): 1644-1649.

[18]Drake C, Nickel C, Burduvali E, et al.The pediatric daytime sleepiness scale (PDSS): Sleep habits and school outcomes in middle-school children[J].Sleep: Journal of Sleep and Sleep Disorders Research, 2003,41(1): 272-278.

[19]Goetz C G, Fahn S, Martinez M P, et al.Movement disorder society-sponsored revision of the unified Parkinson′s disease rating scale (MDS—UPDRS): Process, format, and clinimetric testing plan[J].Movement Disorders, 2007, 22(1): 41-47.

[20]Chang C C, Lin C J.LIBSVM: A library for support vector machines[J].ACM Transactions on Intelligent Systems and Technology (TIST), 2011, 2(3): 27.

[21]Cortes C, Vapnik V.Support vector machine[J].Machine Learning, 1995, 20(3): 273-297.

[22]Lee C P, Lin C.Large-scale linear rank SVM[J].Neural Computation, 2014, 26(4): 781-817.

Optimization of Parkinson′s Scale Using Principal Component Analysis

Lei Shaozheng1,2, Wang Chongjun1,2, Xie Junyuan1,2

(1.Department of Computer Science and Technology,Nanjing University, Nanjing, 210023, China; 2.State Key Laboratory for Novel Software Technology, Nanjing University, Nanjing, 210023, China)

Western scales are a significant basis for assessment of Parkinson′s disease(PD), while these scales contain a large number of cross-duplicates scales, which hampers rapid assessment of PD. Therefore, optimizing these wetern scales is significant for rapid diagnosis of PD. And the method of the optimization of Parkinson’s scale based on principal component analysis(PCA) is raised. The weighted projective vector is extracted based on principal component analysis, and scale problems are divided on the basis of the projected vector using local recursive segmentation algorithm based on Ostu threshold, Finally, based on contribution factors(CF), a new scale is designed. Experiment results confirm that the new combinations of scale which accounts for 21% of the original western scales is highly comparable to original western scales for identifying PD support vector machine(SVM).

Parkinson′s disease; optimization of scale; principal component analysis; local recursive Otsu threshold segmentation;projected vector;contribution factor

国家自然科学基金(61105069)资助项目;江苏省科技支撑计划(BE2012161)资助项目。

2014-03-25；

2014-05-12

TP391

A

雷少正(1988-)，男，硕士研究生，研究方向：数据挖掘。

王崇骏(1975-)，男，教授，研究方向：智能信息化处理、分布式人工智能、社会网络分析和嵌入式智能系统，E-mail：chjwang@nju.edu.cn。

谢俊元(1961-)，男，教授，博士生导师，研究方向：人工智能和智能信息化处理。